双破片侵彻耦合载荷对容器壁面的毁伤研究
蓝肖颖, 李向东, 周兰伟, 纪杨子燚
(南京理工大学 机械工程学院, 江苏 南京 210094)
0 引言
当高速破片撞击并穿透充液容器前壁面时,液体中会形成一个很强的压力场,压力载荷作用在容器结构上,导致结构的毁伤,这种现象被称为液压水锤效应[1]。若容器内为易燃液体,则液压水锤效应可能导致燃料箱爆裂、引燃等。
国外在20世纪70年代就有学者开展了液压水锤效应的研究工作,当时的主要工作是对液压水锤效应现象建立工程计算模型,希望能够预测箱体内的压力以及箱体的响应和破坏[2-4]。Ball等[5]利用Piston理论处理流体、固体耦合问题,将容器壁面视作单自由度系统,假设压力波在结构壁面处垂直反射,并结合Yorkvich的冲击波模型和Lundstrom的压力波模型,求出了冲击阶段和拖拽阶段前壁面所受载荷,利用几何非线性力学代码SATANS和有限元代码BR-1HR求解前壁面应变,但结构应变的预测与试验数据不一致。20世纪80年代,Ankeney提出了一个用于水锤分析的近似结构响应模型,Lundstrom[6]将Ankeney的结构响应模型进行推广,编写了UHRSR程序,计算结果与试验结果一致性较好。Fahrenkrog[7]提出了预测容器后壁面裂纹长度的方法,但该方法在低速破片试验中预测结果较为准确。Rosenberg等[8]将液压水锤效应对容器前壁面的破坏简化为破片穿透壁面和流体载荷作用两个阶段,提出了一个用于估计造成前壁面失效的临界速度半经验公式。21世纪以来,大多学者主要通过试验和有限元仿真的方法来研究液压水锤效应。Varas等[9-11]用速度为600~900 m/s的钢制球形破片(直径为12.5 mm)撞击不同充液比的6063-T5铝合金方管,分析不同影响因素下对容器内压力分布和壁面应力的影响。Kwon等[12-13]重点研究了破片撞击油箱后没有穿透油箱后壁面的情况下油箱结构的响应过程,分析了油箱液面高度、流体密度、油箱材料性能、破片质量和速度等参数对箱体结构动态响应的影响,但没有对该过程进行试验验证。Nishida等[14]用6种不同直径的钢球以40~200 m/s的速度撞击充水铝管,并从试验中得出钢球侵彻壁面所需能量的经验方程。
国内对液压水锤效应的研究起步较晚。王海福等[15]用有限元分析软件AUTODYN-2D数值模拟方法,研究不同撞击条件下液箱结构毁伤,得到破片初速、长径比对液压冲量、空穴半径和箱体变形的影响规律。李典等[16]利用有限元分析软件ANSYS/LS-DYNA分析了前壁面所受冲击载荷的类型及过程。孔祥韶等[17]利用AUTODYN软件中的SPH求解器对爆炸破片穿透液舱的过程进行数值模拟,分析破片速度的衰减规律、液舱内板的响应及液体中冲击波压力的叠加效应,但其没有对该过程进行试验验证。李营等[18]对单个球形弹体撞击充液容器的过程进行试验研究,对比了背空靶板和背水靶板在相近速度弹体侵彻作用下的变形特点。
综上所述,国内外目前的研究主要针对单破片撞击充液容器引起的液压水锤效应,但在实际作战中,战斗部爆炸会形成很多破片并同时或先后作用于目标,破片撞击动能、破片分布的密度和作用时间先后顺序对于目标的毁伤都有很大的影响。因此本文主要研究双破片高速撞击充液容器时前壁面、后壁面的毁伤情况,并考虑破片撞击速度、破片间距、撞击时间间隔对壁面毁伤的影响。
1 双破片液压水锤效应数值计算及试验
1.1 数值计算模型
为研究双破片高速撞击充液容器时前、后壁面的毁伤情况,本文使用ANSYS/LS-DYNA软件对该过程进行数值计算。所建立的有限元模型如图1所示,模型由圆筒、前壁面、后壁面、压盘、破片、水和空气域组成。前壁面、后壁面与圆筒、压盘之间均采用自动面面接触,并约束压盘在破片运动方向的位移,破片与前壁面、后壁面之间采用侵彻接触。其中圆筒材料为钢,内径215 mm,外径245 mm,长200 mm;前壁面、后壁面为380 mm×380 mm×4 mm的2024 T4铝合金板,用钢制压盘将其固定在圆筒两端;破片为直径d=9.5 mm的钨球。破片和前、后壁面网格大小为1 mm,圆筒和压盘网格大小为3 mm.
仿真时,为了让空气流入容器内形成气腔,容器周围设有空气域,空气域设置无反射边界条件,空气域和水域共节点。为了防止计算时出现负体积,以及保证计算的精度,同时控制计算时长,在以破片运动轨迹为中线划分5 cm×5 cm的区域进行网格加密,单元尺寸为1 mm,其他区域网格大小为4 mm,如图1(b)所示。
采用Johnson-Cook模型和Gruneisen状态方程描述容器前壁面、后壁面,Johnson-Cook模型考虑了金属材料所承受的大应变、高应变率以及温度效应。其屈服应力表达式为
(1)
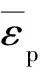
Gruneisen状态方程定义压缩材料的压力为
(2)
式中:S1、S2、S3为us-up曲线斜率的系数,us为冲击速度,up为粒子速度;c为体积声速;γ0为Gruneisen常数;μ=ρ/ρ0-1,ρ为材料当前密度,ρ0为材料初始密度;a为γ0的1阶体积修正。
定义膨胀材料的压力为
p=ρ0c2μ+(γ0+aμ)E0,
(3)
式中:E0为单位初始体积的内能。
采用Plastic-Kinematic材料模型描述钨球破片、钢制压盘和圆筒。前壁面、后壁面、破片、压盘和圆筒的材料参数如表1所示,表中E为弹性模量,ν为泊松比。

表1 固体材料参数
用MAT_NULL模型和Gruneisen状态方程描述水,用MAT_NULL模型和Linear Polynomial状态方程描述空气,其中线性多项式状态方程的压力为
p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E0,
(4)
式中:C0~C6均为常数,当C0=C1=C2=C3=C6=0,C4=C5=γ-1时,即用符合γ律状态方程的气体模型表征空气,γ为比热系数。主要材料参数见表2.

表2 水和空气材料参数
1.2 试验布置
双破片液压水锤效应试验系统由发射装置、挡托装置、测速系统(测速靶和测时仪)、充液容器、背景布和高速摄影机组成,如图2所示。
试验所用破片及充液容器等均与仿真相同。图3为试验所用充液容器,通过螺杆连接圆筒两端的压盘,并用螺栓拧紧。试验时,为保证能同时发射两枚破片,设计了专用的弹托。将两枚破片装在弹托中,通过25 mm滑膛炮发射。发射后弹托分开,释放两枚破片,不影响破片作用于目标。挡托装置能防止弹托打中目标,影响试验结果。测速靶和计时仪能测得破片撞击容器前的速度。用高速摄影机记录破片撞击充液容器的过程,如图4所示。
1.3 试验结果分析
本次试验共计7发,破片撞击速度范围在1 000~1 500 m/s,通过调整装药量使每发撞击速度间隔约100 m/s,试验数据如表3所示。表3中,v0、vr分别表示破片初速和破片剩余速度,Df、Db分别为前壁面、后壁面上的破片穿孔距离(简称孔距),δfmax、δbmax分别表示前壁面、后壁面的最大变形量。其中,第5发和第7发后壁面撕裂严重,无法测出孔距。对比前壁面、后壁面孔距变化可知,破片在充液容器内运动时,两破片间的液体存在高压区,迫使破片产生侧向运动,使后壁面上的破片穿孔距增大。
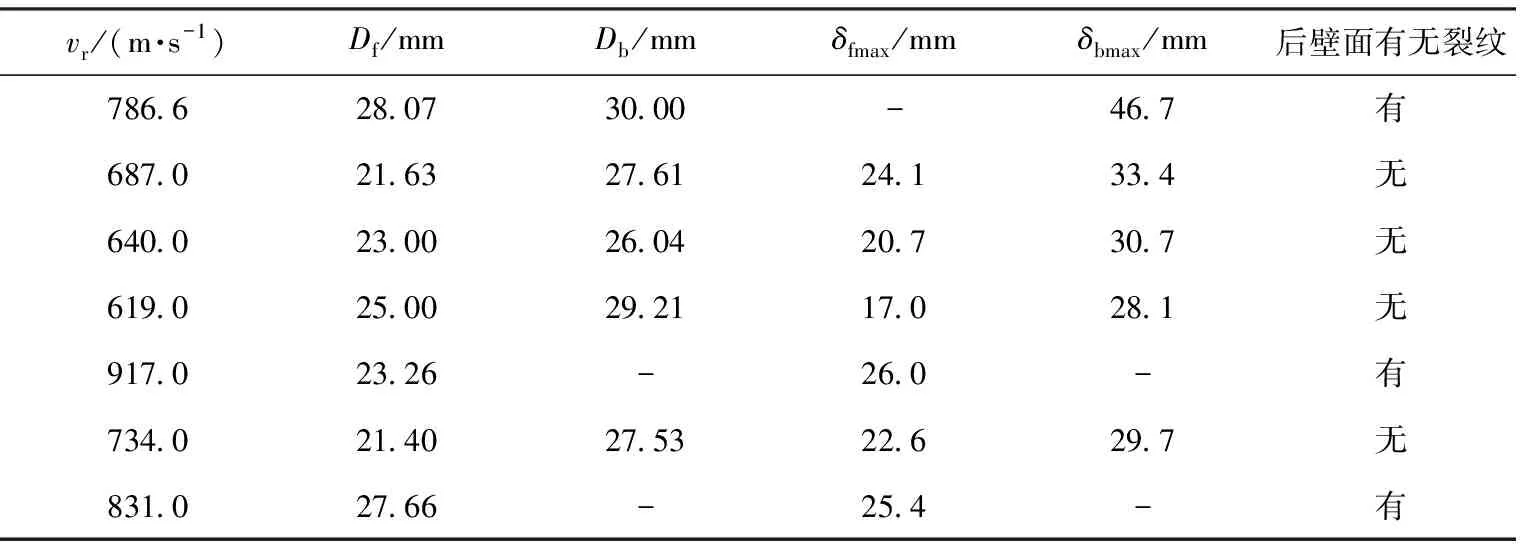
表3 试验情况及结果
图5为选取其中典型5发试验的容器前壁面、后壁面破坏情况。当两个破片撞击速度较低时,前、后壁面均只有塑性变形,无裂纹产生;当两个破片撞击速度增大至1 299 m/s时,后壁面开始产生裂纹,此时裂纹为将两个破片孔连通的一条线;当破片速度增大至1 479 m/s时,后壁面为“花瓣”式开裂。对比第5发和第7发,两个破片撞击速度差别不大的情况下,破片间距较小的第5发后壁面变形比第7发严重,“花瓣”开口更大,裂纹扩展更长。对比每发的前、后壁面损伤可知,后壁面的损伤比前壁面严重,破片的出口孔周围存在广泛的裂纹及明显的塑性变形。主要有两个因素造成前壁面损伤不如后壁面严重:首先,入口面上受到破片的冲击,脉动载荷持续时间较短,而后壁面在破片未到达前不断受到液体中压力波的持续作用;其次,由于液体中的拖拽作用使破片速度明显下降,导致作用于前壁面上的破片速度显著高于后壁面,高速冲击于薄板上会形成一个圆滑的孔,而低速冲击导致在冲击点附近的材料局部变形成撕裂,这些撕裂或者短裂纹可以很容易引起更大的失效。
1.4 试验与仿真结果对比
为获得精确全面的前壁面、后壁面变形数据,采用精度为0.085 mm的MetraScan三维扫描仪对试验容器的前后壁面进行扫描,其中4发典型的前壁面、后壁面变形数据和仿真结果对比如图6所示。当破片撞击速度为1 470 m/s和1 498 m/s时,后壁面撕裂严重,因此图6(c)和图6(d)中间断部分为壁面开裂处。在壁面的边界处,试验和仿真计算中的情况有所差距,边界处的试验变形结果要比仿真大,这是因为试验时通过螺杆将压盘固定在圆筒两侧,提供的约束力不足,导致了在约束处试件发生变形,而仿真时是限制了压盘在破片运动方向的位移。从图6可看出,仿真获得的壁面变形量变化与试验结果趋势相同,试验和仿真获得的前壁面变形量最大误差为7%.
为更充分验证仿真结果的正确性,对试验和仿真计算得到的破片剩余速度进行对比,结果如表4所示,仿真和试验获得的破片剩余速度最大误差为8.98%.
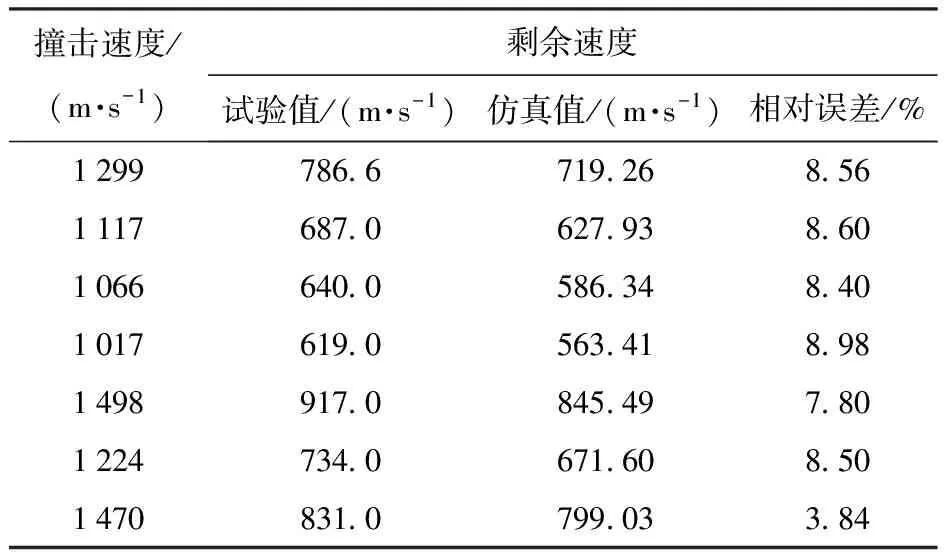
表4 破片剩余速度对比
2 仿真计算结果分析
为研究破片动能、撞击点间距、撞击容器时间间隔对前壁面、后壁面毁伤的影响,共进行了3组仿真。第1组仿真使两个破片撞击点间距为15 mm,撞击速度为800 ~1 600 m/s,每发速度间隔200 m/s,同时撞击充液容器;第2组仿真使两个破片撞击点间距为15~35 mm,每发间距增量5 mm,速度1 200 m/s,同时撞击充液容器;第3组仿真使两个破片撞击点间距为15 mm,撞击速度为1 200 m/s,撞击时间间隔为0~0.2 ms,每发时间间隔增量为0.05 ms.
2.1 前壁面和后壁面所受载荷分析
两个间距为15 mm的破片以1 200 m/s的速度同时撞击充液容器时,不同时刻容器前、后壁面靠水一侧的应力云图如图7所示。由图7可见,前壁面、后壁面所受应力呈环状分布,在两个破片孔周围存在应力集中现象。压力波前沿在140 μs时到达后壁面,壁面中心周围在冲击波的作用下承受较大的应力,在255 μs时破片达到后壁面,破片撞击后壁面,使破片作用位置处附近应力上升。
2.2 破片撞击动能对壁面损伤的影响
为衡量前壁面、后壁面的变形程度,在壁面外凸一侧分别选取沿着x轴、y轴不同位置处的变形量,如图8所示。图9、图10分别为破片撞击点间距Df=15 mm时不同撞击速度下前壁面、后壁面沿着x轴、y轴不同位置处的变形量δ. 从图9和图10中可看出,破片撞击动能越大,壁面变形越大,尤其当壁面出现裂纹之后(v0≥1 200 m/s),破片动能对壁面变形影响更大。
图11、图12分别为破片以800~1 600 m/s的速度、撞击点间距15 mm同时撞击充液容器时前壁面、后壁面的变形云图(不同撞击速度下壁面变形云图的量程相同)。从图11和图12可看出,随着破片撞击速度的提高,壁面变形量增大,并且开始出现裂纹,但破片撞击速度的增大对后壁面的影响比前壁面严重。破片撞击速度的变化主要影响前壁面两个破片孔周围单元的失效,当v0增大至1 600 m/s时,前壁面两个破片孔已连起;当v0为1 200 m/s时,后壁面已经开始出现撕裂,存在两条长裂纹;随着撞击速度的增大,裂纹长度逐渐扩展,且开口更大,v0增至1 600 m/s时裂纹扩展半径为11.3 cm.
2.3 破片撞击点间距对壁面损伤的影响
双破片撞击点间距Df从15 mm增至35 mm(Df与破片直径d的比值为1.6~3.7),以1 200 m/s的速度同时撞击充液容器时,前壁面、后壁面的变形量分别如图13、图14所示。从图13和图14中可看出:破片间距的变化对前壁面几乎无影响,对后壁面影响较大;破片间距越小,后壁面变形量越大,当破片间距增大至破片直径的2.6倍时(Df=25 mm),在x轴不同位置处的壁面变形量将不再减小,但仍然会影响y轴各点处的变形。
由于破片撞击点间距对前壁面变形几乎无影响,只提取了后壁面的损伤结果,如图15所示。由图15可见:两个破片撞击点间距为15 mm时,后壁面有两条长约53 mm的裂纹,呈现花瓣式开裂;破片撞击点间距增大至20 mm时,后壁面其中一个破片孔一侧产生一条14 mm长的裂纹,另一个破片孔一侧裂纹沿着孔延伸;当破片撞击点间距增大至25 mm时,有两条长约7 mm的裂纹;当破片撞击点间距大于25 mm时,后壁面无裂纹产生。
2.4 破片撞击充液容器时间间隔对壁面损伤的影响
图16、图17分别为撞击点间距15 mm的双破片以1 200 m/s的速度先后撞击充液容器时壁面不同位置处变形量的变化(Δt为0~0.20 ms)。从图16和图17中可看出,破片撞击充液容器时间间隔对前壁面、后壁面的变形有较大影响,壁面变形量随着两破片撞击时间间隔的增大而减小,但时间间隔增大至0.10 ms时对壁面变形将无影响。当破片撞击时间间隔Δt从0.05 ms增至0.10 ms时,前壁面最大变形减小14.4%,后壁面最大变形减小14.2%.
不同撞击时间间隔下后壁面变形云图如图18所示(v0=1 200 m/s、Df=15 mm),在该条件下,破片同时撞击充液容器时后壁面会开裂,破片撞击存在时间差时后壁面没有裂纹。破片撞击时间间隔主要影响后壁面破片孔之间单元的失效,当Δt小于0.20 ms时,破片撞击形成的两个破片孔已连至一块;当Δt为0.20 ms时,后壁面两个破片孔之间的单元并未完全失效。破片先后撞击充液容器对后壁面形成的破坏与同时撞击时明显不同,这是因为先撞击的破片已经在壁面形成一个圆孔,在第2个破片到达壁面前,不断有压力脉冲作用于有缺陷的壁面上。
3 结论
本文采用试验和仿真相结合的方法,研究了双破片分别以不同动能、不同间距、不同撞击时间间隔撞击充液容器时对壁面损伤的影响。得到如下结论:
1)破片撞击充液容器的动能越大,壁面变形越大,当壁面出现裂纹时,变形量的增大速度加快。
2)双破片撞击充液容器时,破片的撞击点间距对容器前壁面的变形影响较小,对后壁面影响较大。破片撞击点间距越小,后壁面变形量越大,当破片撞击点间距增大到破片直径的2.6倍时,在x轴不同位置处的壁面变形量将不再减小,但仍然会影响y轴各点处的变形。此外,后壁面裂纹的数量和长度均随着破片撞击点间距的减小而增大。
3)双破片撞击充液容器的时间间隔对前、后壁面变形有较大影响,壁面变形量随着撞击时间间隔的增大而减小,但时间间隔增大至0.10 ms时,对壁面变形将无影响。当破片撞击时间间隔从0.05 ms增大至0.10 ms时,前壁面最大变形减小14.4%,后壁面最大变形减小14.2%.

