一种新的自编码跳码扩谱体制

费顺超， 冯永新， 刘芳， 周帆

(1.沈阳理工大学 研究生学院, 辽宁 沈阳 110159; 2.中国电子科技集团有限公司第47研究所 军品事业部, 辽宁 沈阳 110032;3.沈阳理工大学 信息科学与工程学院, 辽宁 沈阳 110159)

0 引言

在复杂电磁环境中，通信系统的抗干扰性、鲁棒性是保证己方数据通信链路的基础。随着数据链技术的发展，越来越多的抗干扰技术应用到数据链建设中。其中，扩频技术是重要的抗干扰手段。相比于其他扩频系统，直扩(DS)系统具有频谱密度低、抗截获性好、抗多径能力强的特点，广泛应用于信息化弹药数据通信链路中。

通信截获、干扰技术的发展为DS系统在军事通信中的应用提出了新的挑战，对DS数据链抗截获性、抗干扰性提出了新的要求。

为了提高DS系统的抗截获、抗相关干扰性能，可以使直扩码在满足跳变间隔小于累计时间的条件下伪随机地跳变，提高链路的安全性。文献[1-4]先后研究了基于可编程器件的跳码扩谱技术。跳码扩谱可分为预编码扩谱(PESS)和自编码扩谱(SESS)[5-7]。PESS使用固定跳码图案，使伪码序列定期更换，接收过程中，相关处理使用的本地伪码按照跳码图案规律性变化，结合DS系统同步捕获、跟踪处理办法，实现系统的同步。与PESS相比，SESS采用本地信码作为码序列的索引。信码的随机性变化使得SESS具有强于PESS的反侦察、抗相关干扰能力。与此同时，码序列的随机变化为系统同步带来困难，降低了SESS系统的工程可实现性[8-9]。

为了提高DS系统的抗干扰、抗截获性能，改善SESS系统的工程可实现性，本文在分析SESS系统构成及原理基础上，借鉴差分跳频通信技术提出了差分自编码扩谱(DSESS)技术，对DS、PESS、DSESS系统的异同点进行了理论分析，并对3种扩谱方式的性能进行了仿真验证。

1 DSESS原理

根据理论极限(1)式可知，在低信噪比环境中，可通过增加累计时间的方式检测扩频伪码序列。

(So/No)=(Si/Ni)2TW，

(1)

式中：(So/No)、(Si/Ni)分别为侦察接收机的输出和输入信噪比，So、Si分别为输出、输入信号功率，No、Ni为输出、输入噪声功率；T为累计时间；W为DS信号带宽。根据(1)式，通过使伪码序列跳变，可提高扩谱系统的抗截获、抗干扰性能。

SESS系统中，利用无冗余信码序列变化的无序性来实现跳码扩频，其实质是利用前n个信码比特作为第n+1个信码的扩频码。SESS系统的工作流程为：在发射端，信码一路输入扩频调制器，另一路输入移位寄存器组，由移位寄存器组形成的扩频码在调制器中对信码进行调制，得到扩频信号，经射频调制、功率放大，由天线发射出去；在接收端，将接收的信号降频后进行解扩解调，恢复出基带数据。SESS系统原理框图如图1所示。

SESS最大优点是跳码图案和扩频伪码受信码控制，跳码的码集是动态变化的，跳码图案无重复周期，使扩频序列的理论周期为无限长，伪码序列被破译的可能性几乎为0. 随机变化的伪码序列同样为收发双方的码同步提出挑战。由于扩频码直接受信码控制，相邻伪码之间没有约束关系，难以实现收发信号实时同步。如果隔跳或每跳插入引导码或导频，或周期性地发送同步头等勤务信息，将影响原有的无冗余设计，且使用了军事通信中忌讳的导频或勤务跳，将降低通信系统的反侦察和抗干扰性能。

为了解决SESS中码序列变化带来的同步困难问题，借鉴差分跳频体制提出了DSESS技术，利用G函数伪随机地选择扩频码序列，接收方根据逆G函数映射关系，利用前后码序列的相关性解调数据信息，从而在保证军事通信中通信系统反侦察、抗相关干扰能力的同时，提高系统的工程可实现性。DSESS通信系统原理如图2所示。

在发送端，当前时刻的码序列控制字由前一时刻码序列控制字和当前时刻的数据信息决定。G函数将数据信息映射为与之对应的码序列控制字，选择出下一跳所使用的伪码序列。设序列集中序列个数为M，则一个伪码序列负载的最大信息量为log2M. 若信息速率为Rb，则跳码速率的最小值为Rb/log2M.

在接收端，根据通信双方预设的伪随机序列集，通过并行多支路循环相关方式，获得最大的相关输出，由G函数的逆运算解调出接收的数据信息。与DS、SESS系统相比，DSESS系统利用伪随机序列的相关性，以及序列与信码的映射关系，根据检测到的伪码序列，既可解调输出数据信息，减少了因为同步引起的系统开销。

伪码序列选择的随机性和均匀性是决定DSESS系统抗截获性的重要指标。参考文献[10-11]，使用基于m序列、Reed-Solomon(RS)码及混沌序列yn的G函数算法，计算当前信号的伪码序列控制字Cn，Cn=G(Cn-1,Xn,yn,m,CRS)，G(·)为码序列选择函数，Xn为数据信息，Cn为码序列控制字，CRS为前行纠错信道编码。当前伪码序列由待传输的数据信息和上一跳使用的伪码序列决定。由混沌序列y(n)和m序列得到经过扰动处理优化的混沌序列Yn，将其与待发送的数据信息Xn相异或，计算得到数据序列Zn. 根据序列集中序列个数M及序列子集数k，得到用于选择控制的参数Q=M/k和p=m1+2m2+…+2h-1mh.G函数运算过程为

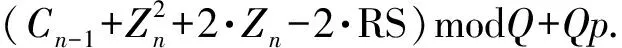
(2)

Cn与两跳前频率序列控制字Cn-2判别，如果两值相异，则候选值Cn；否则，进行候选值修正：

Cn=(Cn-2+Q)modQ.

(3)

通过G函数的反变换利用前后码序列控制字的相关性可以解调出所发送的数据信息。解调依赖于G函数的可逆性，即逆G函数,计算伪随机序列子集间隔变量ΔH及相邻伪随机序列控制字差值Δd，利用解析函数译码集合{(ΔH,Zn)}，解析出Zn，与混沌序列异或运算，得到发送的数据信息：

Xn=Zn⊕Yn，

(4)

式中：⊕为异或运算。

逆G函数的数学表达式为

Xn=G-1(Cn,Cn-1,Yn,m,RS).

(5)

G函数正变换和逆变换如图3所示。

接收端搜索伪随机序列，采用多支路并行循环相关结构，各条支路使用不同的伪随机序列，通过循环相关运算，将时域相关转换到频域计算，利用可编程器件的快速计算能力，快速得到相关结果。利用逆G函数解调输出数据信息。

2 3种跳码扩谱系统的比较

PESS、SESS和DSESS 3种扩谱系统的跳码方式既有相同点又有不同点，根据各个体制的原理进行分析，表1列出了3种系统异同点的比较。

3 抗截获及抗相关干扰性能

3.1 抗载波估计

DS信号的载波估计方法包括平方倍频法、自相关累积法、互相关累积法等。以平方倍频法为例，进行系统抗载波估计性能分析。

设接收到的跳码信号为

(6)

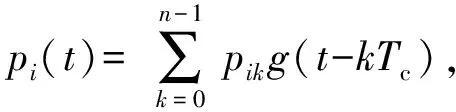
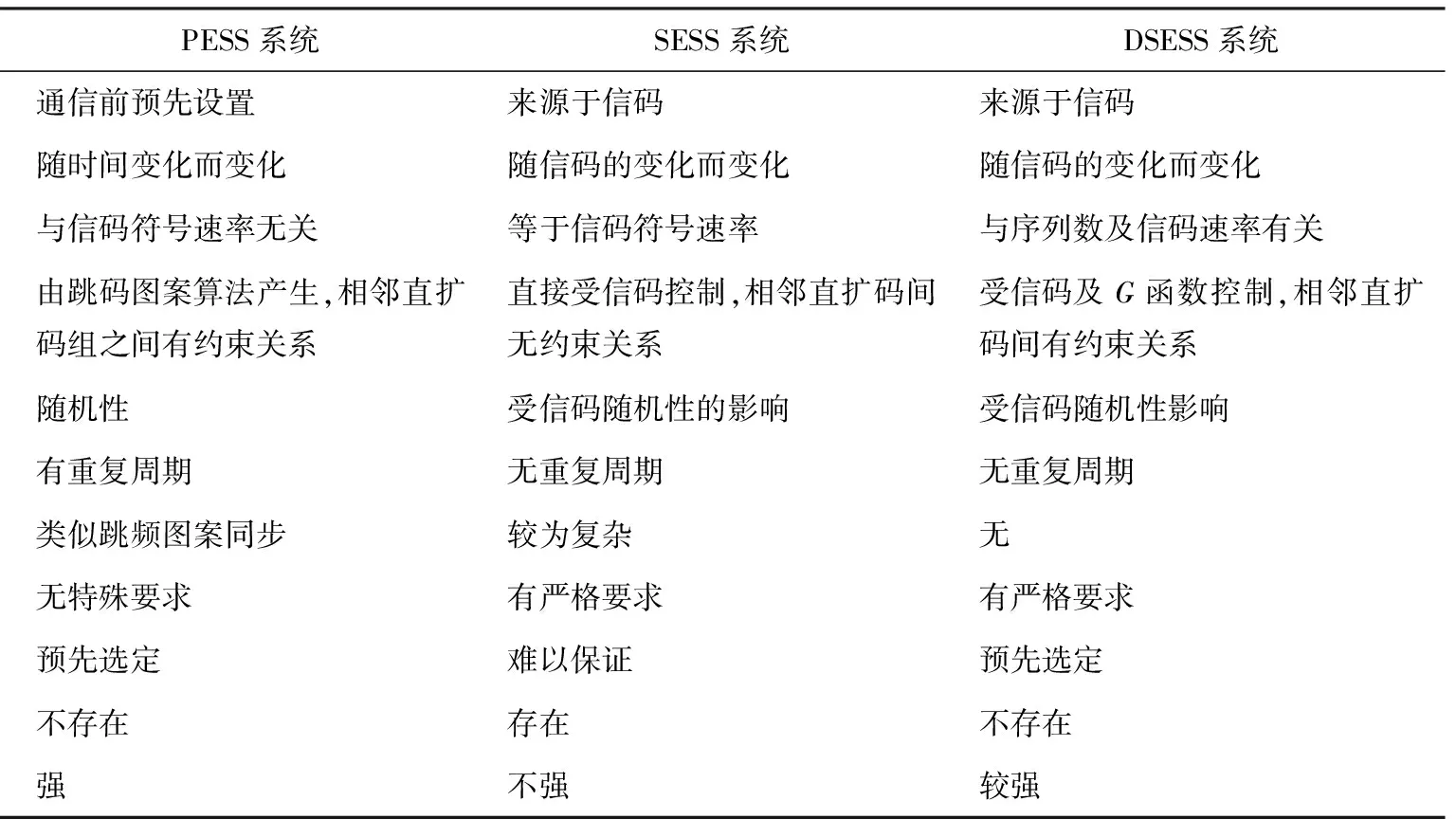
表1 3种跳码扩谱系统异同点的比较

式中：s(t)为发射信号；S为信号功率；ω0为载波频率；n(t)为宽带噪声；pi(t)为第i个伪码序列；pik为第i个伪随机序列的第k个码元；g(t)为门函数；Tc为码元符号持续时间。

根据平方倍频法，对接收信号进行平方处理，可得：

y(t)=s2(t)+2s(t)n(t)+n2(t)=
2S·cos2(ω0t)+2s(t)n(t)+n2(t)=
S+S·cos(2ω0t)+2s(t)n(t)+n2(t).

(7)

根据y(t)的第2项可知，将处理后信号经带通滤波处理，可得载波倍频分量，从而获得跳码信号的载频。平方处理去除了码元电平高低对载波的影响，因此，DSESS系统的抗载波估计性能与DS系统相同。

3.2 抗码周期估计

码周期估计方法包括自相关法、二次谱法、倒谱法以及高阶累积量法等。其中，时域自相关法、二次谱法、倒谱法分别利用信号在时域、频域的相关性估计伪码周期，适用于短周期伪码的估计。在相同数据长度下，高阶累积量法呈现更大的估计方差，但设备复杂，计算量大，不适用于复杂战场环境。本文以时域自相关法估计码周期为例。

以τ表示延时量，为接收信号相对于发送信号的延时量。自相关输出为

(8)

由于伪随机序列的周期性，随着延时量τ的变化，DS信号的自相关函数在延时量等于码周期的整数倍时出现相关峰，相邻两个相关峰之间的时间间隔等于扩频码的周期，从而获得伪随机序列的周期长度。

对于PESS信号，由于跳码图案具有周期性，通过长时间的统计，可以获得伪随机码周期。但是对于DSESS信号，直扩码随着信码的变化而随机变化，延时τ后自相关函数输出无相关峰，即使通过长时间的统计，由于跳码图案的非周期性，也难以估计出码周期。因此，DSESS系统的抗伪码周期估计性能优于PESS和DS系统。

3.3 抗码速率估计

码速率估计方法包括时域延迟相乘法、循环谱法和高阶统计量估计等方法。以典型的延迟相乘法为例，该方法利用伪随机序列的相关性，将相关输出变换到频域，在与扩频码码速率成正比的位置处出现离散谱线，通过检测该离散谱线的位置即可快速估计出码速率。

运算过程如下：

1)延迟τ，计算相关值：

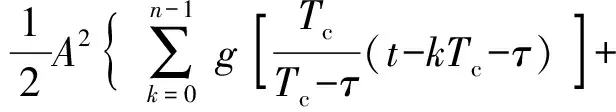
(9)

式中：A为信号最大幅值；ck为第k个伪码；⎣·」为向下取整；g为门信号；φ为相位差。

2)低通滤波，滤除2次谐波：

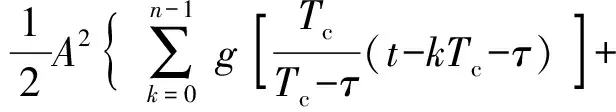
(10)

3)周期图法计算延时相乘后的功率谱密度：

(11)

由(11)式可知，功率谱密度在ωc的整数倍处有离散的脉冲信号，通过谱线检测得到码速率的估计值。

在DSESS系统中，由于直扩码的随机跳变，当截取的处理信号包含跳变的两个序列时，cn与cn-1的相关性将发生变化，使功率谱密度的第2部分不再是包络为sinx/x的连续谱，增大功率谱密度第1部分离散谱线的分析难度。同时，(9)式～(11)式中只考虑了接收信号的有用信号部分，若增加噪声等干扰信号的影响，则码速率估计的难度将进一步增大。因此，DSESS系统有助于提高系统的抗码速率截获性能。

3.4 抗码序列估计

码序列估计是截获数据信息、实施相关干扰的前提条件。对码序列的估计方法有相关函数法、特征值分解法、神经网络法和最大似然估计法等方法。DS信号伪码码型估计中，因伪码是固定不变的，通过对接收信号进行连续监测，可以提高伪码码型的截获概率。DSESS系统中，扩频伪码从单一码型变为多个码型，并且伪码的选择由具有随机性的信码决定，使得伪码变化具有非周期性，间接提高系统的扩频增益，使得跳码扩谱具有更强的反侦察、抗截获能力。

以多重互相关方法为例[12]，分析DSESS系统的抗码序列截获能力。多重互相关估计方法需要在估计伪码周期的前提下，将接收信号以伪码周期分段，利用分段互相关平均估计伪码同步起始点。在此基础上，估计伪码序列。算法步骤描述如下：

1) 按照截获的伪码周期将接收信号进行分段。假设信号总长度为L，估计的伪码周期为L0，共分成l段，每段k个采样点，第i行第j列信号为Sij. 用矩阵表示信号为

(12)

2) 计算分段数据向量间的相关函数，相关信号的第i行第j列元素为rij，得到相关矩阵R：

(13)

3) 求不同k值下矩阵R中所有元素的绝对值之和nk.

4) 取绝对值之和的最大值nkmax，其对应的k值为信息码与伪码的同步起始点。

5) 采用多重互相关平均估计伪码序列。

跳码系统中码序列的变化使得步骤2无法得到类似DS信号的相关矩阵，从而步骤3得到的nkmax不一定是真实的最大值。因此，无法对伪码序列进行有效的估计。

PESS系统中，假设码序列集中码序列的个数为M，则跳码系统的抗码序列截获能力相对于常规DS系统至少要提高M倍。相对于PESS系统，DSESS系统伪码序列变化的随机性更强，使得系统的抗码序列截获能力强于常规DS系统以及PESS系统。

3.5 抗跳码图案估计

对于跳码系统，要想实现有效的相关干扰，必须估计出跳码图案。对于DSESS系统，准确地估计出码周期、码速率、码序列是跳码图案估计的前提。通过以上分析可知，码周期、码速率估计中，通过长时间的积累、递推运算有可能得到估计结果，但码序列的估计难度较大。即使得到估计跳码图案需要的参数，考虑跳码图案估计的实时性，使DSESS体现出较强的反侦察、抗截获能力。

3.6 抗相关干扰能力

相关干扰就是指干扰信号的码型、码长、载频甚至相位与通信信号一样或类似，利用伪码序列的相关性，对DS信号实施相似信号干扰[13-15]。由于干扰信号的相似性，使得干扰信号可以大部分甚至全部进入接收机解调环路，使接收机无法准确解调出数据信息，达到拖延甚至中断通信的效果。通常将处理增益作为衡量系统抗相关干扰能力优劣的指标之一。处理增益Gp定义为接收机相关器输出信噪比和接收机相关器输入信噪比之比，即

(14)

对于噪声干扰、单音干扰、脉冲干扰等信号形式，直扩码序列具有一定的扩频处理增益，使系统具有抗非相关干扰能力[16-17]。对于相关干扰信号，由于干扰信号与发送信号具有相似结构，使得DS系统相对于干扰信号不具有扩频处理增益，失去抗相关干扰能力。有效的相关干扰是以有效的侦察截获为前提，当敌方难以获取DS信号的参数时，就无法实施相关干扰，从这个意义上讲，DSESS系统有利于抗相关干扰。若DSESS系统中伪码序列的个数为M，假设被截获的码序列个数为J，此时可用的伪码序列个数为M-J，此时总的扩频处理增益为

G=10lg(M-J)+10lgGp.

(15)

当码序列完全被截获时，J等于M，此时系统将失去处理增益。通过对DSESS系统抗截获能力的分析可知，完全截获系统的所有参数几乎是不可能的。因此，DSESS系统将体现出强于DS、PESS系统的抗相关干扰能力。

4 DSESS系统仿真分析

通过仿真，分析DSESS码速率估计、码周期估计、码序列估计、抗干扰等性能。采用时域自相关估计码速率和伪码周期，采用基于主元分析(PCA)的矩阵分解法估计码序列。通过对比宽带噪声、部分频带噪声、单音干扰、相关干扰仿真环境下系统的数据信息传输误码率，分析DS、PESS和DSESS系统的抗非相关干扰和相关干扰能力。

仿真采用蒙特卡洛方法，仿真工具采用数学仿真软件MATLAB 2014，采样率为262.144 MHz，伪码速率为16.384 Mbit/s，信息速率为3 kbit/s，跳码速率为500 Hop/s，输入时长为10 ms的数据，伪码序列个数为64(采用截短的P码)，仿真环境的信噪比区间为-20～0 dB，信噪比取值间隔为1 dB, 对每个信噪比样点仿真100次，得出仿真平均值。

4.1 抗伪码周期、伪码速率估计

分析发现，通过时域自相关法得到的峰值与峰值的间隔距离，可以估计出DS信号伪码周期、伪码速率。估计中，使用峰均比(PAR)作为码周期、码速率估计的主要测量参数，表示相关峰值功率与平均功率之比。PAR越大表示峰值越明显，越容易辨识。信道噪声逐渐增大过程中，信噪比逐渐变小，PAR逐渐变小，参数估计的准确性降低。仿真结果如图4所示。

根据仿真结果可知，随着信道噪声的减小，信噪比逐渐增大，PAR值逐渐增大，伪码周期估计的准确性增加。对于DS系统，当信噪比大于-11 dB时，可以较为准确地估计出伪码周期。对于PESS系统，伪码序列的跳变增加了伪码周期估计的难度，在一定程度上破坏了伪码的相关性，通过延长统计时间的方法得到估计的伪码周期，但估计准确率相对DS系统较低。对于DSESS系统，伪码跳变由信息码决定，信息码的无序性提高了系统的抗伪码周期估计性能，即使通过延长统计时间的方法仍然无法有效估计出伪码周期，具有较好的抗伪码周期估计性能。

在相同的系统参数、信道环境下，DS、PESS、DSESS系统的抗伪码速率估计性能如图5所示。

由仿真结果可知，DSESS系统的抗伪码速率估计性能优于PESS和DS系统。在噪声功率较大的环境中，可以通过增加相关累积时间的方法提高估计准确性。然而，对于DSESS系统，伪码序列“无规则”地跳变，破坏了信号的相关性，增加了谱线检测的难度，提高了码速率的抗截获性。

4.2 抗码序列估计

DS信号面临的威胁包括截获和干扰。在截获码序列的前提下，才可能进一步获取数据信息或实施有效的相关干扰。伪码序列的估计是扩谱对抗的关键，可用误码率指标评价系统的抗码序列估计性能。DS、PESS、DSESS系统的抗码序列估计性能仿真如图6所示。

仿真中选择的伪码序列长度为4 096个码片。PCA矩阵分解法通过建立的矩阵对伪码序列进行估计。DSESS系统中，PCA方法建立的矩阵由不同的伪码序列组成，分段数据向量间的相关性较差，无法有效估计出伪码系统，有效提高了系统的抗码序列估计性能。PESS系统中，当信噪比小于-3 dB时，PCA方法无法有效估计伪码码型，具有一定的抗码序列估计能力。对于DS系统，当信噪比大于-9 dB时，PCA方法可以有效估计出伪码码型，系统采用的伪码为周期短码，抗码序列估计性能较差。综上所述，由于DSESS系统码序列变化的随机性，提高了系统的抗码序列估计能力，使得系统的抗码序列截获能力强于DS系统以及PESS系统。

4.3 抗宽带噪声干扰

DS、PESS、DSESS系统的抗噪声干扰性能如图7所示。在宽带噪声干扰下，DSESS信号的抗宽带噪声干扰性能与伪码码型无关，只与扩频增益、信号功率等参数有关，与伪码码型无关。在相同仿真环境条件下，3种扩谱系统的抗噪声干扰性能相差不大。

4.4 抗部分频带噪声干扰

部分频带噪声干扰指干扰信号的带宽小于DS信号的带宽，宽带噪声干扰与部分频带噪声干扰没有本质的区别，只是信号所占用的频谱宽度不同。

DS、PESS、DSESS扩谱系统的抗部分频带噪声干扰性能如图8所示。当前仿真条件下信噪比为10 dB，根据仿真结果，3种扩谱系统的抗部分频带噪声干扰相当。分析可知，部分频带噪声干扰信号对3种扩谱信号进行了压制干扰，抗干扰性能与码型无关。结论与抗宽带噪声干扰相同。

4.5 抗相关干扰

DS、PESS、DSESS系统的抗相关干扰性能仿真结果如图9所示。在干扰信号影响下，随着干扰信号功率的逐渐变小，接收机的误码率逐渐降低。

对于DS系统，当信噪比小于0 dB即干扰信号的功率大于发射信号时，系统被严重干扰，误码率大于0.45，无法有效传输数据信息。与DS系统相比，PESS系统发射信号按照跳码图案有序传输，可以有效抑制部分相关干扰，当信噪比小于-8 dB时，误码率约为0.40，体现出较好的抗相关干扰性能。对于DSESS系统，当信噪比为-10 dB时，误码率小于0.20，这是因为干扰信号与接收信号的相关性较差，无法形成有效的相关干扰。与DS系统、PESS系统相比，DSESS系统具有优秀的抗相关干扰性能。

5 结论

为了提高跳码系统的抗干扰性、抗截获性，改善其工程可实现性，本文借鉴差分跳频系统，提出了基于G函数的DSESS系统，并对该扩谱系统的性能进行了分析。得到主要结论如下：

1)提高了DS系统的抗截获性能。DSESS系统在保持DS系统频谱密度低等特点基础上，通过G函数使伪码序列根据映射关系伪随机变化，降低由于时间累积可能引起的信号被截获的概率。根据仿真结果，对比分析3种跳码体制的抗干扰性能可知，DSESS系统具有较好的抗截获性能。

2)提高了DS系统的抗相关干扰性能。根据仿真结果，DSESS系统的抗宽带噪声干扰、抗部分频带噪声干扰性能与DS、PESS系统相类似，即抗非相关干扰性能未得到明显改善。但是DSESS系统的抗相关干扰性能明显优于DS、PESS系统，具有良好的抗相关干扰性能。

3)DSESS系统通过G函数可以保证相邻跳之间直扩码的码间相关性，可以有效抑制多径干扰，降低误码传播现象的发生。

4)DSESS系统使伪码序列伪随机的跳变，避免了SESS伪码序列不可预测导致的同步困难问题，改善了跳码系统的工程可实现性。