火箭上升段滚动时域制导控制一体化设计
李 敏,李惠峰,聂文明
(北京航空航天大学宇航学院,北京 100191)
0 引 言
传统的火箭上升段制导控制系统设计是将制导和姿态控制子系统分开设计,通过对各子系统分别设计控制律再进行反复的迭代和整合来满足系统整体的性能要求[1]。这种分离设计形式已经广泛地应用于火箭上升段制导和控制系统,基本可以满足制导精度和控制性能要求[2-3]。然而,由于分离设计自身的局限性,针对制导和姿态控制子系统设计的控制律只能改善各子系统的控制性能,即使反复地协调设计也无法最大程度优化系统整体的控制性能,如制导精度、控制需求等[4-5]。制导控制一体化(Integrated guidance and control,IGC)的概念最早在1983年由Williams等[6]提出,近年来已经成为了制导与控制领域的研究热点之一。不同于传统的制导回路产生制导指令,姿态控制回路进行跟踪并获得执行机构控制量的分离设计方式,IGC设计是将制导和姿态控制子系统作为一个整体进行设计,根据飞行器的运动状态信息直接产生执行机构需用的操纵指令[7]。IGC设计避免了大量的迭代整合,不仅可以减少设计周期和成本,而且具有减少控制量需求、提高控制精度等提升系统整体控制性能的潜力[8]。但是,IGC设计也存在很多难点,如一体化系统建模尚未形成完备的理论体系,系统模型阶数更高、耦合性更强对控制方案设计造成很大困难等。目前,飞行器制导控制一体化设计还没有形成系统的研究体系。现有的文献主要是针对导弹对目标的打击段尝试进行研究[9-11],关于火箭上升段的IGC设计还比较少。
针对火箭上升段制导控制一体化系统,基于最优控制理论设计控制器可以最大程度实现对标称弹道的准确跟踪,同时尽可能减少控制量需求。目前,最优控制方法已经广泛应用于制导控制一体化设计中。Hughes等[12]针对目标拦截IGC问题,采用线性最优控制方法进行IGC设计,但该方法难以满足复杂非线性系统的设计要求。于是非线性最优控制理论成为研究的热点,但其存在难以求解Hamilton-Jacobi-Bellman(HJB)方程的问题。Vaddi等[13]针对寻的导弹IGC问题,采用状态依赖Riccati方程的方法求解HJB方程,但其在线计算量很大。Xin等[14]基于目标拦截IGC问题,采用θ-D的次优控制方法求解HJB方程的近似闭环解,该方法不需要在线求解HJB方程,但其推导过程非常复杂。上述传统的最优控制均需要准确的系统模型,并且没有考虑系统的不确定性问题,系统鲁棒性较差。于是,滚动时域控制(Receding horizon control,RHC)逐渐受到关注。RHC是一种基于最优控制的计算机控制算法,它将全局优化问题转化为有限时域优化问题,通过在线滚动优化完成求解过程。RHC不需要准确的系统模型,且鲁棒性较强,已经广泛地应用于工业控制领域,但在飞行器制导控制领域应用较少[15-16]。彭海军等[17]将RHC策略应用于航天器在Halo轨道之间转移的问题中,通过在线求解Riccati微分方程求解制导律,但其没有考虑控制约束。一般而言,含有多种时域约束条件的滚动时域优化问题的动态特性都是非线性的,很难求得解析解。
基于以上分析,本文针对火箭上升段IGC问题,提出一种基于凸优化理论的滚动时域制导控制一体化设计方法。该方法采用RHC策略进行滚动优化和反馈校正,可以及时弥补模型误差或外界干扰等造成的不确定性。同时利用高效的凸优化算法可以有效地求解含控制约束的优化问题。通过李雅普诺夫稳定性理论证明了该方法的稳定性。相比传统分离设计,该IGC设计方式具有提高系统控制精度,减小控制量需求的潜力。
本文结构如下:第一部分建立火箭上升段IGC模型并对其进行反馈线性化获得面向控制的线性模型。第二部分结合控制约束建立凸优化问题。第三部分采用RHC策略和凸优化算法在线求解控制律并给出了算法稳定性证明。第四部分进行数值仿真。
1 IGC模型
建立火箭上升段IGC非线性模型,采用反馈线性化的方法对其进行精确线性化和解耦获得面向控制的线性模型。
1.1 火箭上升段IGC模型
假设滚转通道姿态为理想的稳定状态,仅研究俯仰通道和偏航通道的制导控制一体化设计问题。本文忽略侧向运动,建立火箭上升段IGC非线性模型为
(1)
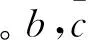
(2)
式中:P为发动机推力,Isp为发动机比冲,g0为地球引力加速度。气动阻力D、升力L和侧力N分别为

(3)
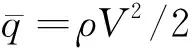
1.2 反馈线性化
IGC模型非线性程度较高,传统平衡点处进行近似线性化方法忽略了系统的高阶项,控制过程中可能会出现较大误差。因此,采用针对非线性系统的精确反馈线性化方法对IGC模型进行线性化和解耦。
选取y=[h,V]T为系统输出量,系统状态量为x=[h,V,θ,α,β,r,q]T,控制输入为u=[Mcy,Mcz]T,将式(1)写为如下仿射形式

(4)
对系统输出y=H(x)=[H1,H2]T进行依次微分运算。通过对高度h进行4次求导,对速度V进行3次求导,控制量u可以显式地出现在如下微分表达式中
H*=b(x)+a(x)u
(5)

(6)
系统相对阶r=4+3=7与系统阶数相等,系统可以进行解耦和精确线性化。
u=a(x)-1(v-b(x))
(7)
引入新的状态变量
(8)
其具体形式为
(9)
经过状态转换,原来的非线性系统模型转化为如下面向控制的线性模型
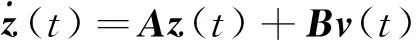
(10)
2 凸优化问题建模
将火箭上升段制导控制一体化(IGC)问题建模为最优控制问题。由于控制约束的存在,系统整体呈现非线性动态,很难求得解析解。凸优化算法作为一种高效的数值解法,可以方便地求解非线性优化问题,且解的收敛性有保证[18]。因此将该最优控制问题进行凸化处理和离散化进而转化为标准凸优化问题。
2.1 凸优化问题描述
式(10)所示的线性模型中,z(t)为系统状态量,v(t)为控制输入。给定参考轨迹xref(t),通过式(8)进行状态转换,得到线性系统参考状态量zref(t)。依照最小化状态跟踪误差和控制输入的原则,设计系统代价函数为

zref(t))+vT(t)Rv(t))dt
(11)
式中:Q和R为加权矩阵,并且满足Q≥0,R>0。t0=0为火箭上升段飞行初始时间,tf为终端时间。火箭飞行的初始条件为x(t0)=xref(t0)=x0,通过式(8)进行状态转换得到线性系统的初始条件为
z(t0)=z0
(12)
原非线性系统控制量为u=[u1,u2]T,给定控制约束的幅值为umax=[u1max,u2max]T,则原系统控制约束为
(13)
将式(7)所示的反馈控制律代入式(13),得到线性系统的伪控制量不等式约束为
(14)
式中:φ(umax,x)=[φ1,φ2]T和ψ(umax,x)=[ψ1,ψ2]T为
(15)
控制约束φ(umax,x)和ψ(umax,x)是关于状态量x的函数,是非凸的。由于初始状态x(t0)=x0是确定的值,初始时刻求得的控制约束φ(umax,x0)和ψ(umax,x0)是常数矩阵,将其作为整个优化过程的控制约束可以实现约束的凸化。式(11)的代价函数和式(12)的初始条件是凸的,满足凸优化问题求解要求。
2.2 离散化
对连续系统进行等时间间隔离散化,选取采样时间为T,则时间区间[t0,tf]被分成如下时间序列
(16)
式(10)的线性系统被离散为如下形式
z[(k+1)T]=Gdz(kT)+Hdv(kT)
(17)
式中:
(18)
式(11)代价函数,式(12)的初始状态条件及式(14)的控制约束做相应的离散变换。则离散化后的凸优化控制问题可以描述为
vT(k)Rv(k)]
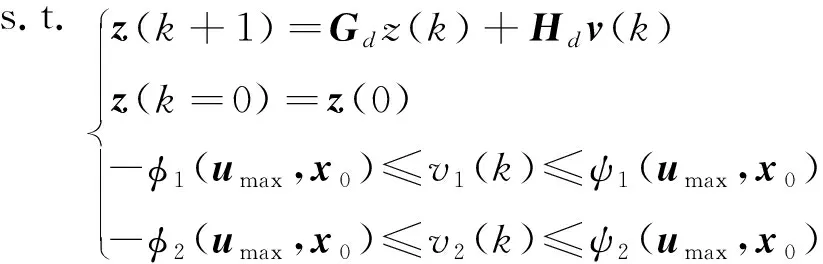
s.t.z(k+1)=Gdz(k)+Hdv(k)z(k=0)=z(0)-ϕ1(umax,x0)≤v1(k)≤ψ1(umax,x0)-ϕ2(umax,x0)≤v2(k)≤ψ2(umax,x0)
(19)
3 滚动时域控制算法
通过滚动时域控制(RHC)算法设计,将式(19)给出的全局凸优化问题转化为有限时域凸优化问题,采用凸优化算法进行求解,结合反馈控制律形成了闭环控制。在优化问题中引入终端惩罚项和终端域来保证系统的稳定性,并给出了证明和分析。
3.1 滚动时域控制算法设计
滚动时域控制(RHC)的基本思想是预测模型、滚动优化和反馈校正。在当前时刻,RHC方法以当前实际状态作为初始条件进行反馈校正并求解有限时域优化问题,然后将解的第一个量用于实际控制中。随着时间的推移进行滚动优化直至完成整个过程。
在当前时刻k,选取预测时域为p,则在有限时域[k,k+p]内,预测模型为
z(k+i+1|k)=Gdz(k+i|k)+Hdv(k+i|k)
(i=0,1,…,p-1)
(20)
式中:z(k+i+1|k)为在k时刻对k+i+1时刻的状态预测量,v(k+i|k)为在k时刻对k+i时刻的控制输入预测量。当前的实际状态量x(k)作为有限时域优化问题的初始条件,通过式(8)进行变量转换得到线性模型的初始条件为
z(k|k)=z(k)
(21)
由于k时刻的状态x(k)是确定的值,将其代入式(14)求得的控制约束φ(umax,x(k))和ψ(umax,x(k))是常值矩阵,将其作为[k,k+p]时域内的控制约束,则在有限时域内,可以保证控制约束是凸的。
有限时域最优控制问题的稳定性一般难以保证,根据准无限时域预测控制的思想[19],在优化问题中引入合适的终端域和终端惩罚项可以保证该有限时域优化问题的稳定性。稳定性证明将在后续部分给出。在代价函数中增加终端惩罚项,则有限时域[k,k+p]内的代价函数变为

E(z(k+p|k)),i=0,1,…,p-1
(22)
式中:
(23)
Qf为终端惩罚项加权矩阵且Qf>0。在优化问题增加终端状态约束
(z(k+p|k)-zref(k+p))∈Ω
(24)
式中:Ω为终端域,它迫使系统在有限时域的末端回到平衡点的某一领域内。
于是得到第k时刻的滚动时域控制凸优化问题表达式为

E(z(k+p|k))
(i=0,1,…,p-1)
(25)
采用凸优化算法求解式(25)的有限时域凸优化问题,得到如下k时刻的预测状态序列z(k)为
z(k)=[z(k+1|k),z(k+2|k),…,z(k+p|k)]T
(26)
和预测控制序列v(k)为
v(k)=[v(k|k),v(k+1|k),…,v(k+p-1|k)]T
(27)
将式(27)代入式(7),可得反馈控制律为
u(k)=[u(k|k),u(k+2|k),…,u(k+p-1|k)]T
(28)
下面给出火箭上升段IGC控制问题的滚动时域控制算法步骤。
1)初始化。给定采样周期T和预测时域p,选择合适的加权矩阵Q,R,离线计算终端惩罚项加权矩阵Qf和终端域Ω。令初始时刻k=0。
2)优化。获取系统k时刻的实际状态x(k),通过式(8)的状态转换,得到初始条件z(k)。在时域[k,k+p]内求解式(25)所示的优化问题,得到式(28)的反馈控制律u(k)。
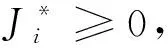
3)迭代。将解序列u(k)的第一个解用于实际的控制中。令k=k+1。如果k+p 假设2.U是紧的和凸的,X是连通的,并且平衡点(0,0)包含在集合X×U内部。 引理1[20]. 当假设1和2成立,若非线性系统关于控制u是仿射的,并且在域X中可以精确反馈线性化,并可以求得一个反馈控制器v=Kz使得GK:G+HK渐近稳定,则得到非线性控制器 κ(x):u=a-1(x)(Kφ(x)-b(x)) (29) 对于由κ(x)控制的非线性系统有 1)系统轨迹满足 (30) 式中:F(x,u)=xTQx+uTRu,E(x)=xTQfx,对应到z-v坐标中为F(z,v)=zTQv+vTRv,E(z)=zTQfz,其中Qf满足 (31) 2)对于任意Qf>0,可以找到常数σ∈(0,∞),使得 Ω:={x∈Rn|φT(x)Qfφ(x)≤σ} (32) 是系统的一个不变域,且Ω和函数E可以作为准无限时域预测控制优化问题的终端域和终端惩罚函数。 引理2[20]. 在k=0时刻开环优化问题(25)有可行解,在不考虑外部扰动和模型误差的情况下,问题在任意k>0时刻也有可行解。 定理1. 若假设1和假设2成立,式(1)的非线性系统可以精确反馈线性化,并且在k=0时刻开环优化问题(25)有可行解,则该滚动时域控制设计可以保证闭环系统是渐近稳定的。 证. 非线性系统(1)可以进行精确的反馈线性化,根据引理1,可以计算出终端惩罚矩阵Qf和终端域Ω。根据引理2,可以保证在每一时刻k>0,式(25)中优化问题都有可行解。 将代价函数作为李雅普诺夫函数,在k时刻,代价函数的优化值为 E(z*(k+p|k)) (33) 在k+1时刻,优化问题由可行解计算的代价函数值为 E(z(k+1+p|k+1))= F(z(k+p|k+1),v(k+p|k+1))+ E(z(k+1+p|k+1))= E(z*(k+p|k))-(z*(k|k),v*(k|k))+ F(z(k+p|k+1),v(k+p|k+1))+ E(z(k+1+p|k+1))-E(z*(k+p|k)) (34) 由式(33),式(34)变为 p|k+1),v(k+p|k+1))+E(z(k+1+ p|k+1))-E(z*(k+p|k)) (35) 又因为z*(k+p|k)=z(k+p|k+1)且z*(k+p|k)∈Ω,根据引理1,可以推出 (36) 结合式(35)和式(36)可知 F(z(k+p|k+1),v(k+p|k+1))+E(z(k+ 1+p|k+1))-E(z*(k+p|k))≤0 (37) 则式(35)变为 (38) 且优化解不会差于可行解,式(38)变为 (39) (40) 根据文献[21]中引理4.3,推出 (41) 为校验所提滚动时域制导控制一体化控制方法的有效性和鲁棒性,以某二级火箭上升段为研究对象进行仿真。上升段全程飞行时间为122 s,在飞行67 s后进行一二级分离。火箭飞行终端高度为89 km,终端速度为4538 m/s。一级控制力矩约束为|Mc1|≤1068000 N·m,二级控制力矩约束为|Mc2|≤3890000 N·m。仿真过程中采样周期为T=1 s,预测时域p=20。式(22)所示代价函数为状态误差与控制需求最小。由式(9)可知,状态量为高度和速度的各阶导数,其数量级呈递减趋势。综合考虑性能指标与各状态量需求,并考虑适当偏重高度和速度状态的权重,尽可能减小轨迹跟踪误差,选取适当的控制矩阵。一级飞行阶段控制器加权矩阵为 (42) 二级控制器加权矩阵为 (43) 终端惩罚加权矩阵Qf和终端域Ω为 (44) 仿真过程中控制器参数设置保持不变。各级发动机均采取耗尽关机方式。首先在标称大气的情况下,采用滚动时域IGC设计方法进行仿真,并与传统分离设计的思路进行分析对比,进一步校验该方法的有效性。另外,在有气动干扰的情况下进行仿真,校验了该方法的鲁棒性。仿真在Matlab环境中进行,其中凸优化问题的求解使用凸优化工具箱CVX。 在标准大气的情况下,设计滚动时域IGC控制器并进行数值仿真。此外,基于传统分离设计思想,姿态控制回路同样采用滚动时域控制方法设计控制律,制导回路采用PID方法设计制导律并进行数值仿真。通过IGC和传统分离设计两种思路的对比仿真,进一步校验了滚动时域制导控制一体化设计方法的有效性。仿真结果如图1~6所示。图中线型标注中,标称表示给定的标称弹道,IGC表示制导控制一体化设计,G & C表示传统分离设计思路。 火箭飞行高度和速度的跟踪曲线如图1所示,跟踪误差曲线如图2所示,弹道倾角和质量曲线如图3所示。由图1~3可知,基于本文滚动时域IGC的控制方法可以实现对标称弹道的轨迹跟踪,且高度跟踪误差不超过10 m,速度跟踪误差不超过 图1 高度和速度变化曲线Fig.1 Curves of altitude and velocity 6 m/s。而传统分离设计方式的轨迹跟踪误差较大,尤其在火箭一二级分离、质量突变后,质心运动受到较大影响,轨迹跟踪误差越来越大,高度跟踪误差最大达到104 m,速度跟踪误差最大为22 m/s。图4和图5分别为火箭上升段姿态角和角速率变化曲线,由图4~5可知,IGC设计和传统分离设计两种方式都能保证火箭上升段飞行过程中的姿态稳定,总体来说,基于IGC设计的姿态角变化更加平缓。 图2 高度和速度跟踪误差变化曲线Fig.2 Curves of altitude and velocity tracking errors 图3 弹道倾角和质量变化曲线Fig.3 Curves of flight path angle and mass 图6是控制力矩曲线,两种设计方式都能满足系统控制约束。但是,从图6也可以清晰地看出,基于IGC设计的俯仰力矩比传统方式更小。偏航力矩存在较小的波动,IGC设计的偏航力矩的峰值比传统方式减少约46%,整体来说,IGC设计的偏航力矩需求更小。由以上分析可知,在满足姿态稳定的情况下,IGC相比传统分离设计方式,可以提高制导精度,减少控制量需求。 图4 攻角和侧滑角变化曲线Fig.4 Curves of angle of attack and sideslip angle 图5 偏航和俯仰角速率变化曲线Fig.5 Curves of yaw and pitch angle rates 图6 偏航和俯仰控制力矩变化曲线Fig.6 Curves of yaw and pitch control moments 为校验所提滚动时域IGC控制方案的鲁棒性,考虑在有气动干扰的情况下进行仿真分析。引入±20%的气动力干扰和±40%的气动力矩干扰,分别在气动系数正、负拉偏两种情况下进行数值仿真。 仿真结果如图7~11所示。从图7~10可以看出,在有气动干扰的情况下,该方法也能以较小的跟踪误差实现对标称轨迹的跟踪且能保证姿态角稳定,高度跟踪误差不超过50 m,速度跟踪误差不超过15 m/s。 图7 气动干扰下高度和速度变化曲线Fig.7 Curves of altitude and velocity with aerodynamic disturbance 图8 气动干扰下高度和速度跟踪误差变化曲线Fig.8 Curves of altitude and velocity tracking errors with aerodynamic disturbance 图9 气动干扰下攻角和侧滑角变化曲线Fig.9 Curves of angle of attack and sideslip angle with aerodynamic disturbance 图10 气动干扰下偏航和俯仰角速率变化曲线Fig.10 Curves of yaw and pitch angle rates with aerodynamic disturbance 图11 气动干扰下偏航和俯仰控制力矩变化曲线Fig.11 Curves of yaw and pitch control moments with aerodynamic disturbance 图11为控制力矩曲线,在有气动干扰的情况下,控制力矩相对无干扰情况下的控制量有小幅波动,但飞行全程仍然严格满足控制约束,没有出现饱和。由以上分析可知,本文的滚动时域IGC控制方案不仅能较好地处理控制约束,而且有较好的鲁棒性。 针对传统火箭上升段制导与控制系统分离设计方式存在的问题,提出一种基于凸优化理论的滚动时域制导控制一体化设计方法,并基于李雅普诺夫稳定性理论证明了系统的闭环稳定性。该方法采用RHC策略进行滚动优化,基于当前状态信息进行反馈校正,能及时弥补模型误差或外界干扰等造成的不确定性。同时基于凸优化理论对优化问题进行凸化和离散化,并采用凸优化算法进行数值求解,有效解决了含控制约束的优化问题的求解。数值仿真表明,该IGC方法具有较好的动态性能,且具有一定的鲁棒性。与传统分离设计方式相比,火箭上升段IGC设计可以减少设计周期和成本,并且可以提高系统的整体性能。3.2 稳定性分析
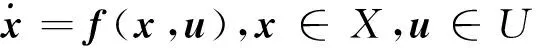

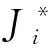
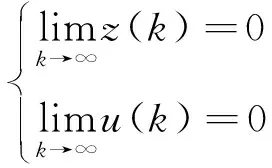

4 仿真校验


4.1 有效性仿真

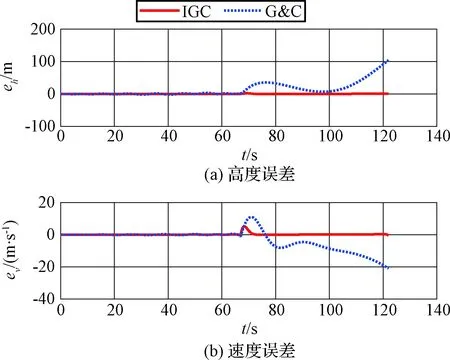

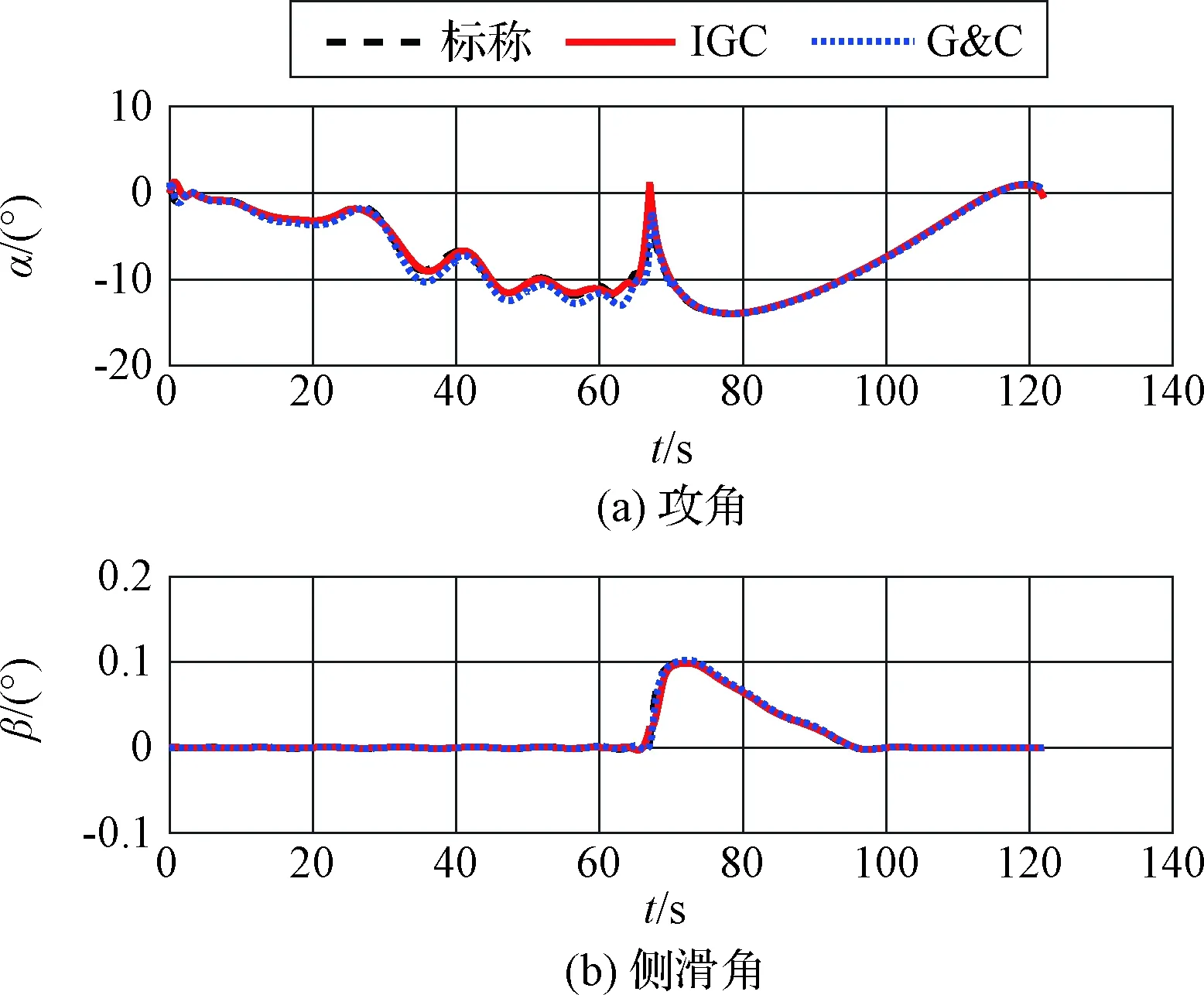

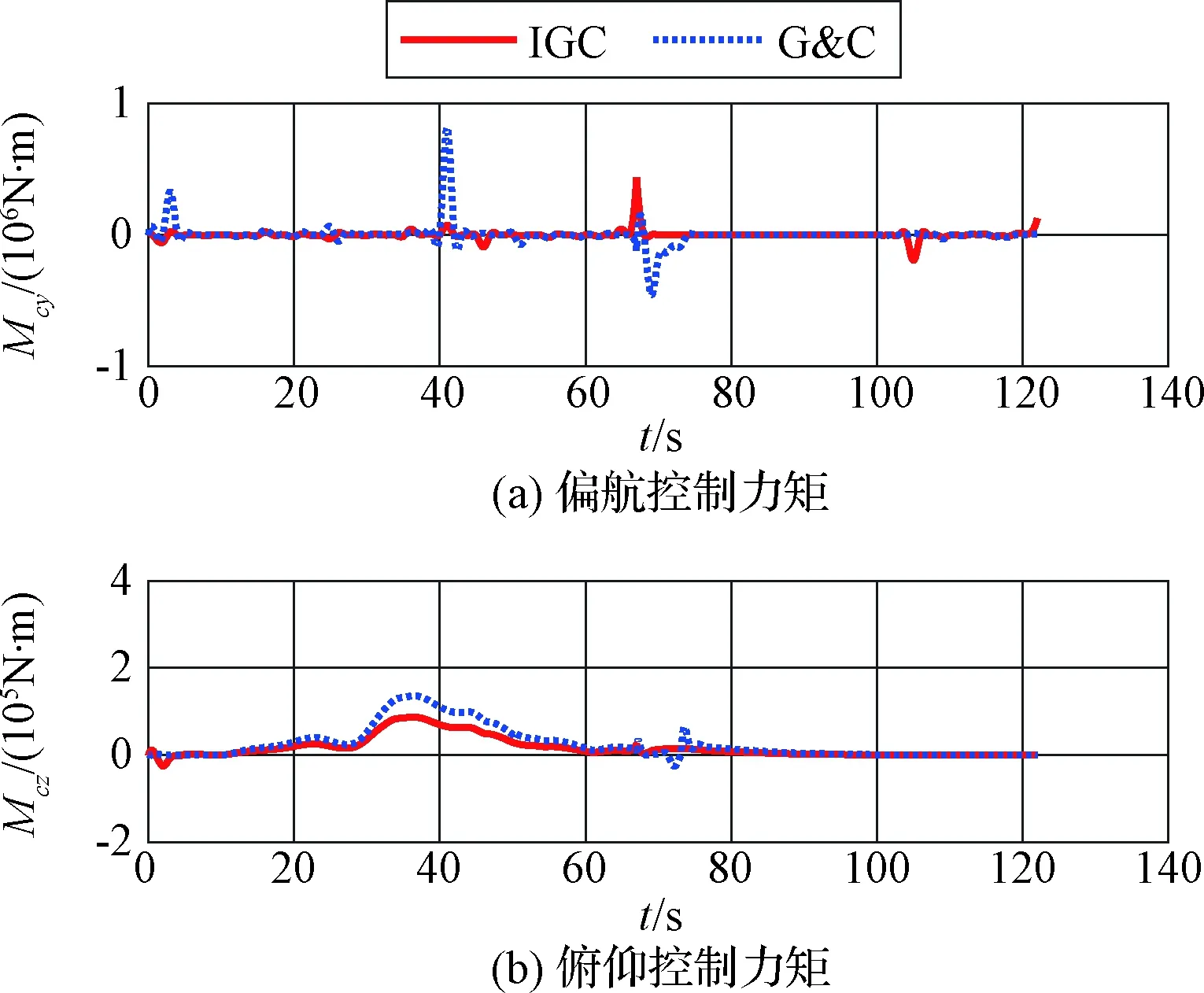
4.2 鲁棒性仿真
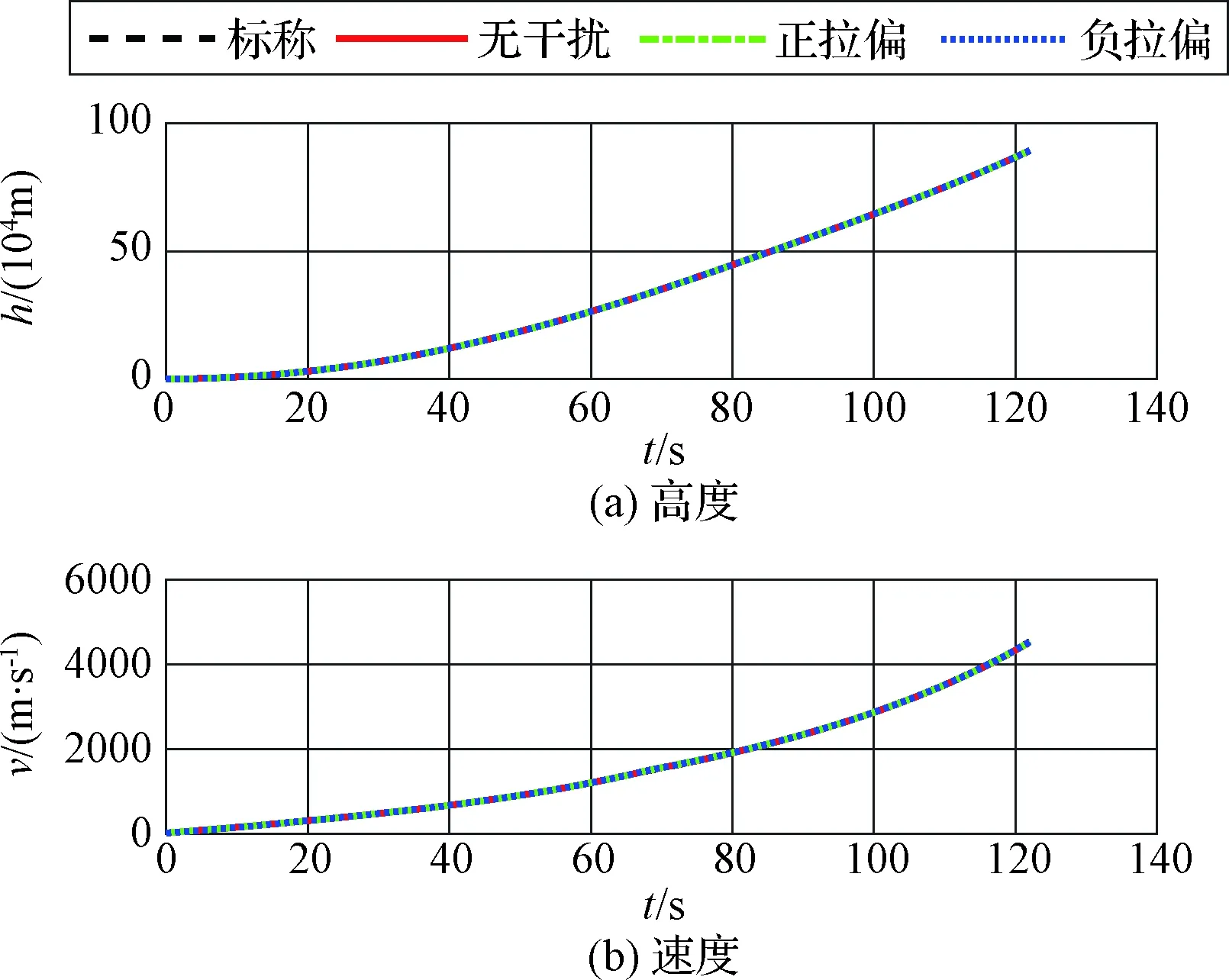
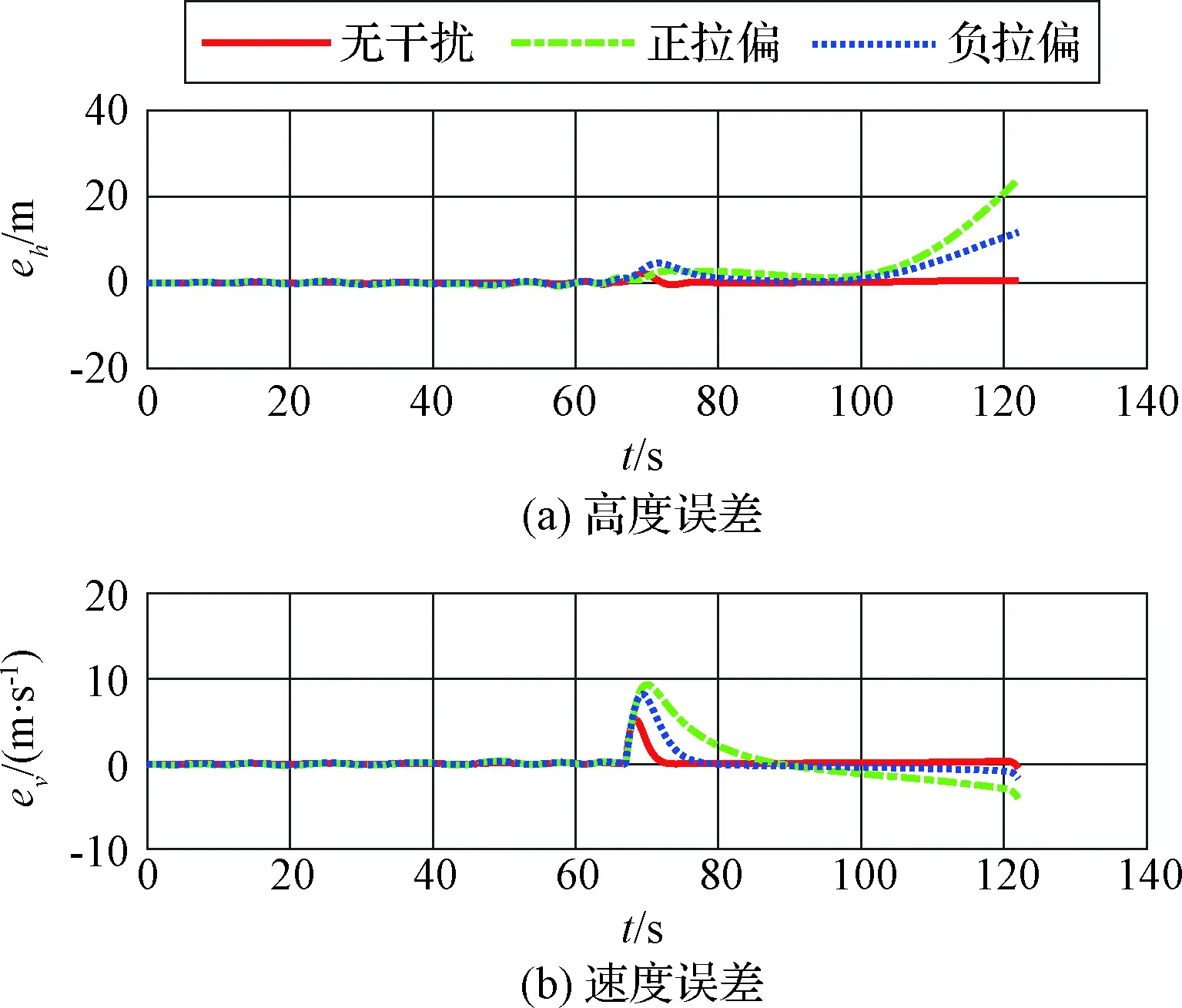


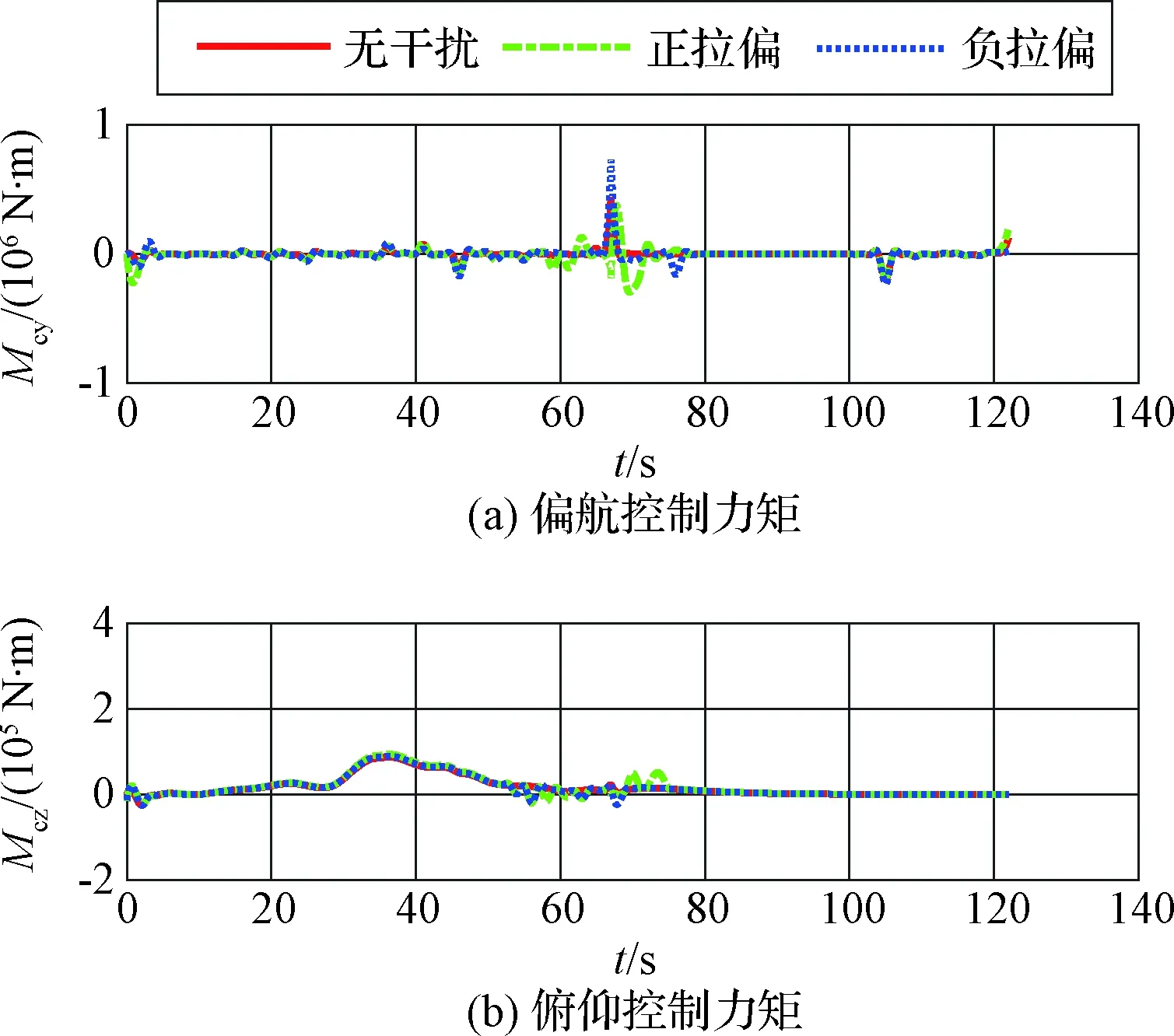
5 结 论

