基于地轴矢量解算的SINS无纬度支持自对准方法
郑振宇,周爱军,唐 君,徐轩彬
(海军大连舰艇学院, 大连 116018)
0 引 言
捷联惯导系统(SINS)初始对准的最终目标是确定载体坐标系相对导航坐标系的姿态关系。现有的初始对准理论与方法,如基于卡尔曼滤波的对准方法、罗经对准法以及近年来提出的基于最优化的惯性系对准方法(OBA方法)等[1-4],在方法应用中都需要精确的纬度信息支持。目前,对准所需纬度信息主要源于卫星或无线电定位手段,然而,对于水下、地下、密林等无线电信号覆盖不到,或在高架桥、高层楼宇遮挡导致信号覆盖微弱的区域,要获得纬度值并非易事,因此,研究无纬度支持下的对准方法成为近年来初始对准研究的一个重要方向。
针对静止基座下未知纬度对准问题,文献[5]提出利用导航系下重力与地球自转角速度矢量的夹角估计纬度,再利用估计纬度采用传统解析方法实现粗对准。在晃动基座下,文献[6]提出利用重力矢量在惯性空间的角位置关系确定纬度,再利用估计纬度进行传统意义的惯性系对准,并分析了纬度估计的精度与对准精度。上述方法均采用先进行纬度估计再对准的两阶段模式,后者以前者为基础,增加了方法应用的复杂性;另外,纬度估计与对准都源于矢量观测信息,观测信息被重复利用,从信息处理的角度,对准效率有待提高。那么,能否利用矢量观测信息直接实现无纬度支持下的对准解算呢?

1 基于地轴矢量解算的对准思路
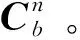
1.1 静止基座下的对准思路


(1)

(2)
1.2 晃动基座对准思路

2 静止基座下直接解析对准方法
2.1 直接解析对准算法

(3)
式(3)中未出现纬度值,同时矩阵各行向量均为单位向量且相互正交,无需额外进行正交化处理,相对传统的解析式对准方法更具工程实用性。
2.2 与传统解析法的统一关系
将式(3)变形后可得到:
(4)

(5)
显然,式(5)即为传统的解析对准方法解算模型。因此,直接解析对准方法在重力矢量与地球自转角速度矢量模约束与两个矢量夹角约束条件下即转化为传统解析式对准方法。
2.3 精度分析
(6)
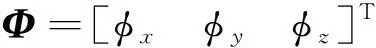
(7)
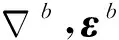
(8)
当不考虑矢量模误差时,有μ1=g,μ2=gΩcosL,此时,式与传统解析对准的误差模型一致[8]。
当考虑矢量模误差影响时,以加速度计观测模为例,根据模解算关系有:
(9)

1/μ1=[1-δfb/(2g2)]/g
(10)
以加速度计误差为1000 μg为例,经计算由矢量模误差引起的姿态误差约为0.2″,因此,误差分析中可以忽略模观测误差的影响。
下面分析重力矢量指向误差引起的姿态误差。假设重力矢量指向偏差引起的纬度误差为δL,则μ2=gΩcos(L+δL),带入式中的方位误差项得:
(11)
泰勒展开并忽略二阶小量后得到由重力矢量指向偏差引起的方位误差项为:
(12)
以地球表面最大垂线误差30″为例,假设纬度为45°,陀螺常值漂移误差为0.1 (°)/h,加速度计零偏为1000 μg,则由此引起的方位误差仅为0.14″。因此,在实际应用中无需考虑矢量模误差以及重力矢量指向误差的影响,直接解析对准方法与传统解析对准方法具有相同的理论极限精度。
3 基于地轴矢量解算的晃动基座自对准方法
3.1 对准基本流程
(13)

(14)
(15)
重力矢量观测在某一时间点上可以获得该时刻导航系天向轴矢量Ub0:
(16)

3.2 地轴矢量的三矢量几何解算方法

图1 重力矢量载体惯性系视运动Fig.1 Gravitational apparent motion in b0-frame

1)计算三个矢量的差分矢量Δg1与Δg2:
(17)
2)根据叉乘关系计算地轴方向矢量:
u=Δg1×Δg2
(18)
3)根据矢量关系建立差分矢量Δg1与Δg2的中垂线矢量l1及l2:
(19)
4)计算三个矢量间的中心位置∑g1与∑g2:
(20)
5)建立l1及l2的中垂线方程组:
(21)

3.3 地轴矢量的四元数解算方法

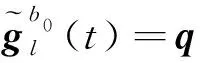
(22)


(23)

(24)

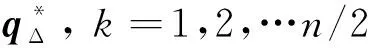
(25)

(26)
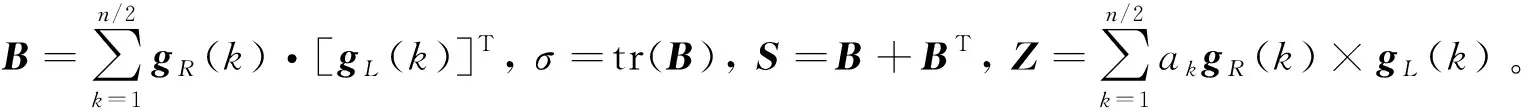
(27)
4 实验验证
4.1 静止基座对准实验验证
4.1.1仿真实验
以静止基座下100 s的加速度计、陀螺数据为解算数据,仿真中设陀螺仪常值漂移为0.1 (°)/h,随机漂移0.01 (°)/h;加速度计零偏为1000 μg,随机噪声为100 μg。蒙特卡洛仿真次数设为100次,仿真步长设为0.01 s。分别采用文献[5]与式(3)的直接解析对准方法进行同等条件对准解算,解算后传统方法需要进行正交化解算,最终解算误差以及100次Matlab解算消耗时间结果如表1所示。由结果可知,两种解析式对准方法的误差均值差别不大,直接解析法的方位误差均方差要小于传统方法;同时,由于直接解析法无需纬度估计,且无需正交化过程,仿真运算耗时小于传统方法,解算效率较高。

表1 两种解析式对准方法精度及运算时间比较Table 1 Analytic alignment methods’ run time and precisions
4.1.2转台静止基座实验
实验采用SGT-3型三轴多功能实验转台,实验对象为自研光纤捷联航姿系统,捷联系统安装于试验转台,令X轴指内框轴、Y轴指中框轴、Z轴指外框轴。将转台内中外框置零,保持静止10 min,在此基础上内、中框位置不动,外框转至45°位置,保持静止10 min;再分别令外框置于90°、135°、180°、225°、270°、315°,连续采集8个方位位置的IMU数据,完成对准采集实验。采集成后,分别截取8个方位下平台稳定后5 min的数据,并进行直接解析式对准解算,8次解算误差如表2所示,其中方法1为传统解析算法,方法2为直接解析方法。由表2可看出,在无纬度支持条件下直接解析式对准精度与传统解析方法基本相同,具有较强的实用价值。

表2 转台下8位置解析对准精度Table 2 Analytic alignment precisions of eight positions on turntable
4.2 晃动基座对准仿真校验
仿真中惯性器件参数设置及蒙特卡洛样本数与4.1节相同,对晃动基座下基于地轴矢量的对准方法进行验证分析。仿真中模拟基座航向ψ、纵摇θ及横摇γ角呈周期性变化,幅度分别为4°、5°与7°,摇摆周期分别为7、5与6 s。设杆臂长度为(0.05、0.05、0.05 m),横荡、纵荡和垂荡引起的线速度也呈周期性变化,其模型为:
VDi=ADiωDicos(ωDit+φDi)
(28)
其中,ADx=0.02m/s,ADy=0.03 m/s,ADz=0.2 m/s,ωDi=2π/TDi,TDx=7 s,TDy=6 s,TDz=8 s,φd为[0 2π]上服从均匀分布的随机相位。对准解算时间为200 s,地轴矢量解算方法分别采用三矢量定姿及基于四元数的优化算法,称为未知纬度1及未知纬度2方法。
首先,不引入观测滤波环节,重点考查两种方法的有效性,方位对准误差分布结果如图2所示,姿态误差均值及均方差结果如表3所示。由结果可以看出,两种方法水平对准结果近似重合,精度上基本一致,但方位误差相差较大,说明方法采用不同的轴向矢量解算方法仅影响方位解算精度对水平对准精度几乎没有影响。由图3可看出方法1的方位对准精度较差,对准解算超差现象严重,分析其原因,是由于对准时间较短,方法1构建的中垂线方程易形成病态方程,矢量观测未进行滤波,观测噪声过大,容易形成奇异解,造成方位对准失效[12]。然而方法2的地轴矢量解算来源于更为全面的观测数据,且采用最优姿态解算算法,算法解算稳定性较好,方位对准精度较高。

图2 无滤波下摇摆基座仿真实验方位对准精度分布Fig.2 Simulation results distribution of alignment azimuth precision without filter
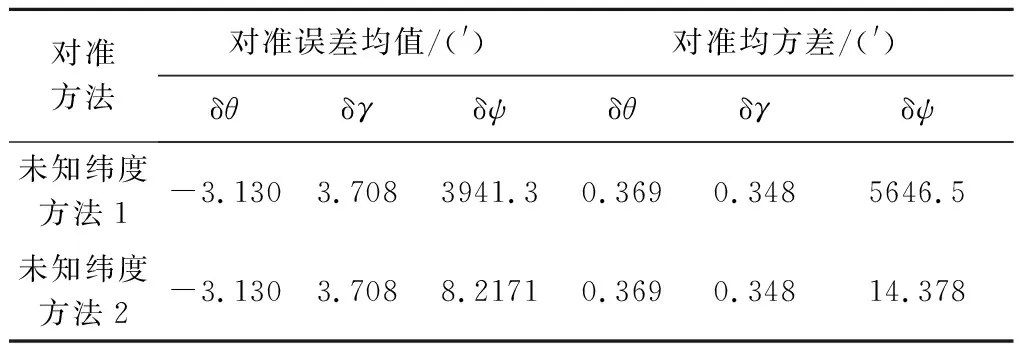
对准方法对准误差均值/(')对准均方差/(')δθδγδψδθδγδψ未知纬度方法1-3.1303.7083941.30.3690.3485646.5未知纬度方法2-3.1303.7088.21710.3690.34814.378
其次,对惯性系重力矢量观测引入低通滤波环节,考察滤波后的对准精度情况,滤波器参数设置如表4所示。

表4 低通滤波器参数设置Table 4 Parameter setting of low-pass filter
低通滤波后的对准误差分布见图3,统计结果见表5。不难发现,引入低通滤波环节后重力矢量观测精度得到了提高,对准精度相应得到提高。同时,两种对准方法具有相同的水平对准精度,但基于四元数解算的对准方法的对准误差均值与均方差值都小于几何解析对准方法。

图3 摇摆基座仿真实验方位对准精度分布Fig.3 Distribution of simulation azimuth alignment precision

对准方法对准误差均值/(')对准均方差/(')δθδγδψδθδγδψ未知纬度方法1-3.2541.1970.5230.01030.01074.252未知纬度方法2-3.2541.1971.8930.01030.01071.459
4.3 船载实验验证
在仿真实验的基础上,以海试实验数据为对象检测本文对准方法的实船环境适用性。试验海域为南海某海域,仿真数据源于装载于舰艇上的两套自研光纤捷联航姿系统,其中,一套系统采用GPS位置组合导航工作方式,作为姿态基准,另一套系统输出数据作为仿真数据源,如图4所示。系统IMU光纤陀螺的零偏稳定度优于为0.01 (°)/h,加速度计零偏稳定度优于50 μg。对准解算时间为200 s,数据解算起始时间每次向前推进30 s,共进行10次对准解算,结合姿态基准得到姿态误差,10次对准解算误差结果如图5所示。
可以看出,船载实验与仿真实验结果的精度分布特点基本一致。两种对准方法的水平对准精度相同,横摇角对准误差在8′以内,纵摇角对准误差在2′以内;采用本文方法的方位对准精度(对准误差小于55′)要高于基于三矢量解析的对准方法(对准误差小于75′),且方法2对准结果的稳定性也优于方法1,表明基于四元数的地轴矢量解算方法在未知纬度条件下对准应用中具有较强的优越性。

图4 船载实验航姿系统配置Fig.4 Ship-borne fixing of IMU testing

图5 船载实验对准误差分布Fig.5 Distribution of ship-borne test alignment errors
5 结 论
本文将无纬度支持对准问题转换为对地轴矢量在参考坐标系下投影的解算问题,并分别建立了静止基座以及晃动基座条件下的解决方案。仿真实验与转台实验分别验证了静基座直接解析方法的有效性以及相对传统解析对准方法的高效性。针对晃动基座下的地轴矢量解算问题,提出了一种基于旋转四元数的轴向矢量优化解算方法,仿真实验与船载实验验证了该解算方法相对于三矢量几何解算方法的优越性。下一步将针对重力矢量观测的干扰问题引入实用有效的预滤波方法,以进一步提高方法的对准精度。

