油套管特殊螺纹密封性能数值仿真研究
张 颖,练章华2,周 谧,林铁军2,罗伟强
(1.四川轻化工大学 机械工程学院,四川自贡 643000;2.西南石油大学 油气藏地质及开发工程国家重点实验室,成都 610500)
0 引言
随着天然气勘探开发的不断深入和井下工作环境的日趋复杂,具有较高气密封性的特殊螺纹接头在气井开采中的应用日益广泛。特殊螺纹采用金属对金属接触密封形式,通过密封面之间的过盈接触提供较大的密封接触压力,以保证气密封性能。特殊螺纹金属对金属密封的密封面结构类型甚多,很多在实践中性能欠佳,逐步退出市场。经过理论研究和现场密封失效的调研[1-7],认为气井用油套管特殊螺纹扣金属对金属密封面主要有两种结构形式:锥面对锥面密封和球面对锥面密封。目前,国内外针对特殊螺纹密封性能的评价手段主要采用有限元法和试验评价研究的方法[8-13]。许志倩等[14-15]选用锥面对锥面主密封结构型式加工试件,开展了特殊螺纹密封面结构的气密性试验,测试了密封预紧力、密封面的表面粗糙度、密封面接触宽度等对气密封性能的影响。张瑞萍等[16]针对油管柱在压裂工况条件下,分析了轴向动载对特殊螺纹接头联接强度和密封性能的影响。Bradley等[17-18]详细介绍了高温高压酸性气井中,特殊螺纹扣气密封的设计和检测方法,并指出螺纹接头密封结构设计必须考虑密封面的耐磨性以及接触压力的分布必须满足密封要求。
总体上,我国在油套管特殊螺纹密封设计、制造、产品信誉、创新专利以及相关基础理论研究等方面,与国外相比还存在一定差距。国外著名公司持续改进或推出管端新结构特殊螺纹扣[19-21],但是几乎不公布其依托或支撑的机理或设计理论。国内油套管特殊螺纹的开发,基本基于反复的加工和实验室评价,对特殊螺纹密封面结构密封机理缺乏基础性研究。本文利用有限元方法,建立特殊螺纹主密封结构接触力学模型,详细分析锥面对锥面、球面对锥面密封结构形式的接触应力分布,提出优化改进方案,并引入密封接触能理论,对特殊螺纹密封结构的密封性能进行对比分析。
1 锥面对锥面密封结构数值仿真分析
1.1 等锥面线性密封结构
由于特殊螺纹密封面接触属于高度非线性问题,很难对其进行精确的理论求解分析,可以借助计算机强大的计算能力,对特殊螺纹密封面接触问题开展数值仿真研究。图1示出特殊螺纹扣锥面对锥面密封面有限元模型,其中该特殊螺纹密封面结构采用等锥面结构设计,即公接头和母接头的密封面的内锥角相同,其锥度均为θ。图1中线段AB为螺纹接头的密封面,也称之为密封路径。特殊螺纹密封面结构有限元模型边界条件:采用轴对称模型,母接头外边界固定约束,公接头边界上施加轴向载荷。

图1 特殊螺纹等锥面线性密封结构有限元力学模型
螺纹接头材料为P110T,系各向同性材料,弹性模量为2.10×105MPa,泊松比为0.29,试验测得材料的应力-应变曲线关系见图2。材料的屈服强度805 MPa,材料强度极限为923 MPa。

图2 P110T材料的应力-应变曲线
分别对特殊螺纹接头等锥线性密封结构紧扣后(上扣扭矩为10 kN·m),其内锥角θ为3°~4.5°(内锥角度数为锥角度数的一半),考察接头密封结构的应力分布特征以及密封面路径上的接触应力分布。其有限元力学计算结果如图3所示。图3(a)为内锥角为3°时,上扣完成后,接头密封结构vonMises应力分布云图,可以看出,接头密封结构的最大vonMises应力为768 MPa。其余螺纹接头的密封面内锥角分别为3.5°,4°,4.5°,相应的最大vonMises应力分别为777,785,810 MPa,如图3(b)~(d)所示。可以看出,随着特殊螺纹扣接头密封面内锥角的增加,接头密封结构的vonMises应力也随之增大,当内锥角为4.5°时,接头密封结构的最大vonMises应力超过材料的屈服强度,材料进入屈服阶段。因此,建议特殊螺纹扣锥面对锥面线性密封结构的内锥角设计应该小于4.5°。
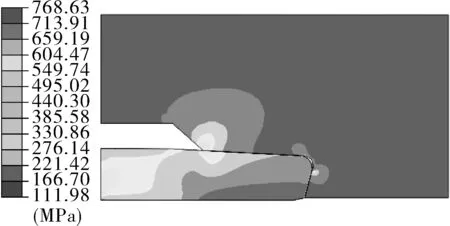
(a)内锥角3°

(b)内锥角3.5°
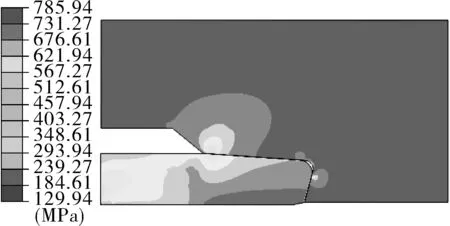
(c)内锥角4°
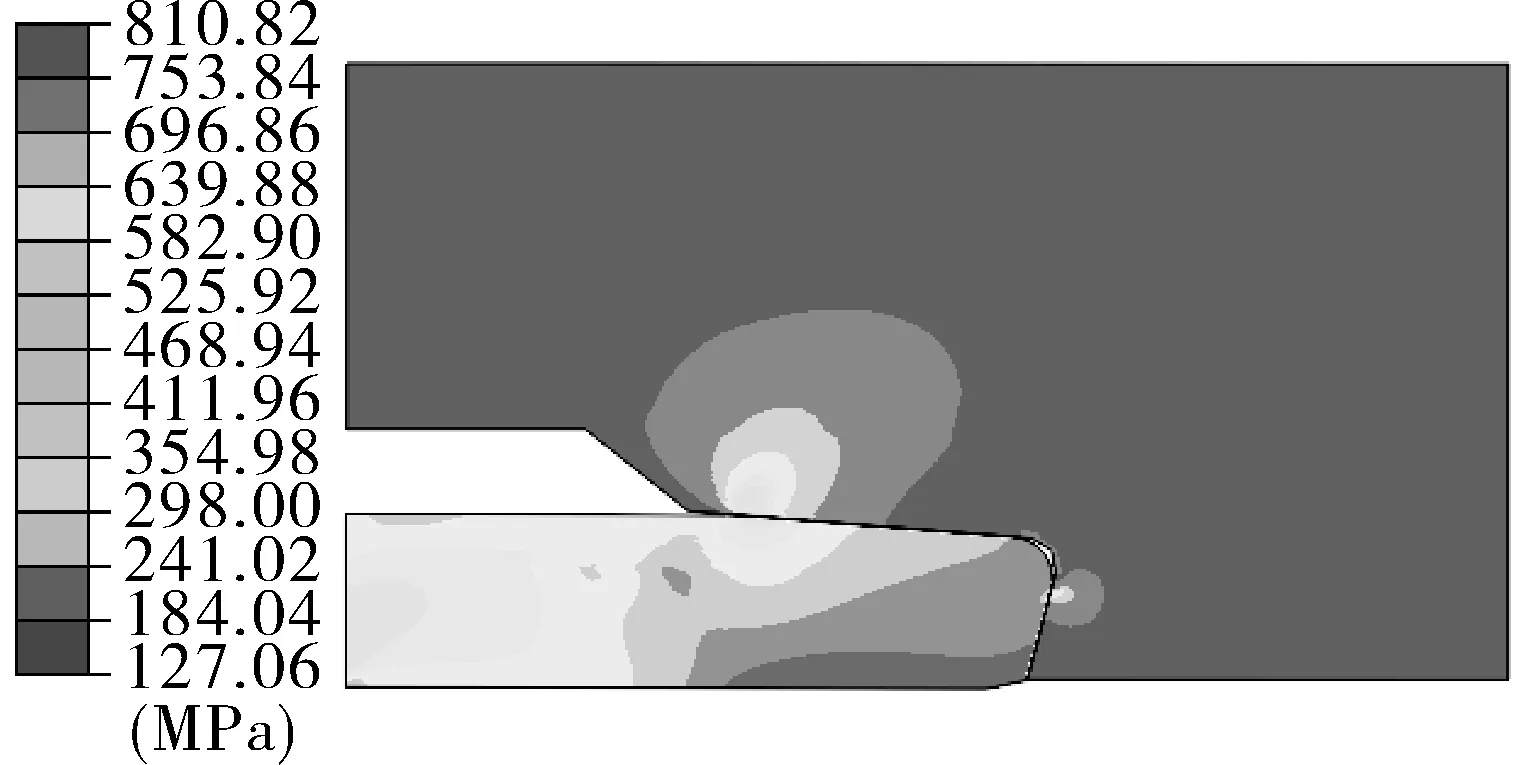
(d)内锥角4.5°
图4为等锥面线性密封结构密封面上接触压力的变化规律曲线。

图4 等锥接触密封面接触压力与内锥角、路径的变化关系
可以看出,随着特殊螺纹扣接头密封面之间内锥角的减小,其接头螺纹密封面的接触宽度增加,但接触压力有所降低。同时,由于增加密封面接触宽度,有利于提高密封能。从图中还可以看出,密封面上的接触应力分布为两端高、中间低,且密封面中部接触应力集中在60 MPa。因此,等锥面密封结构的主要密封位置集中在密封面A,B两个端面位置。在考虑恶劣生产条件下(地层温度>120 ℃,地层压力>75 MPa)油管管柱的长期安全生产,即要求特殊螺纹扣密封压力大于拟密封压力的两倍。那么密封面两端位置接触应力应高于150 MPa。从图4可以看出,当内锥角降低到3°时,密封面B端位置接触应力略低于150 MPa。因此,建议特殊螺纹锥面对锥面线性密封的内锥角设计应该大于3°。综上因素考虑,特殊螺纹锥面对锥面密封结构密封面的设计内锥角推荐为3.5°~4.5°。
从图4还可以看出,由于密封面等锥线性接触的不协调性,在特殊螺纹等锥接触密封面上沿路径AB(见图1)的接触压力分布呈两头大、中间小的特点。且在密封面上A位置点,即接头密封结构大端,接触应力最大。在密封面B位置点,即接头密封结构的最小端,接触应力水平较低。由于油管内气体泄漏路径沿B点至A点,即B点为密封面的密封起始位置。因此,应该设法提高B位置点附近的接触应力水平,从而提高特殊螺纹的密封性能。
1.2 非等锥面线性密封结构
为了提高螺纹接头密封面密封起始位置接触应力水平,本文提出螺纹接头密封结构采用非等锥面线性密封结构设计,如图5所示。图5中,公接头密封面的内锥角为θ1,母接头密封面的内锥角为θ2,并且θ2>θ1,以及a>b,即要求母接头密封面锥角略大于公接头密封面锥角设计。为验证设计密封结构的可靠性,采用有限元软件,计算分析非等锥面线性密封结构特殊螺纹接头密封面上的接触应力分布大小及规律。根据第1.1节数值分析结果,选择公接头密封面内锥角θ1=3.5°,非等锥母接头密封面内锥角θ2分别为3.55°,3.6°,3.7°和3.8°。密封面路径AB上的接触应力分布如图6所示。

图5 特殊螺纹扣非等锥面线性接触密封有限元力学模型
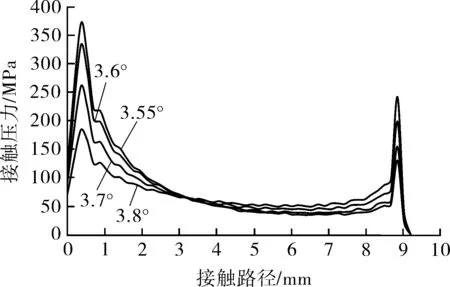
图6 非等锥面线性密封结构密封面上接触压力与母接头内锥角、路径的变化关系
从图6可以看出,采用非等锥线性接触密封结构能够有效改善密封面A,B两端的接触应力峰值。母接头密封面内锥角与公接头密封面内锥角差值越大,密封面A点位置接触应力峰值越小,而密封面B点位置应力峰值越大。当母接头密封面内锥角上升至3.7°时,密封面位置点A和位置点B上的接触应力峰值相当,当母接头密封面内锥角大于3.8°后,密封面位置点A的接触应力峰值明显小于位置点B的接触应力峰值。可以看出,非等锥线性接触密封结构能够有效改善螺纹接头密封面上接触不协调现象,改善密封面上的应力分布。建议在采用锥面线性接触式密封结构中,其接头密封面结构采用非等锥式线性接触密封,且母接头密封面内锥角设计大于公接头密封面设计内锥角5%~8.5%。
2 球面对锥面密封结构数值仿真分析
2.1 密封接触区域与曲线形状关系
在特殊螺纹扣密封结构设计中,球面对锥面的金属对金属密封形式,其球面形状主要分为正弦型曲线、椭圆型曲线和抛物线型曲面。3种曲线的描述方程如下。
正弦曲线:
(1)
椭圆线:
(2)
抛物线:
(3)
假设接头密封面长度为12 mm,密封曲线高度为1 mm,将式(1)~(3)三种曲线绘图表示,如图7所示。
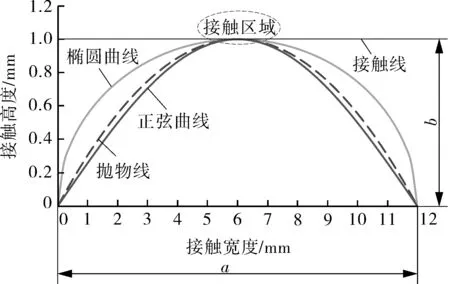
图7 接触曲线形状与接触区域
从图7可以看出,在相同密封结构尺寸a,b时,变形后的接触区域相比,椭圆接触区域最大,其次是抛物线,正弦曲线接触区域最小,因此要获得最宽的接触区域,椭圆曲线为最佳曲线。若考虑接触压力最大,则刚好相反。比较3种密封曲线,如果要求接触面压力最大,可以采用正弦曲线结构;若考虑密封面宽度较宽和压力较大,可以采用椭圆曲线结构。
2.2 椭圆密封结构
图8示出特殊螺纹球面对锥面的椭圆密封面有限元力学模型。图中特殊螺纹母接头密封面采用锥面结构设计,特殊螺纹公接头密封面采用椭圆结构设计。长半轴长度为a,表示密封面长度,短半轴长度为b,表示密封面的密封过盈量。其中椭圆长半轴与母接头密封面具有相同的内锥角。显然,增大公接头和母接头的过盈配合量,可以增加密封接触压力,但在较大的过盈量下,接头会产生较大的塑性变形。
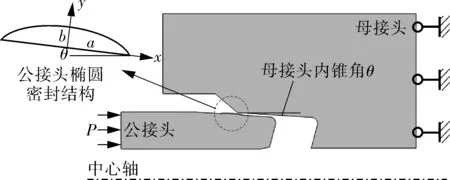
图8 特殊螺纹扣椭圆密封面结构有限元力学模型
本文通过对比公接头椭圆密封面在不同的椭圆率下,即不同的椭圆短轴与长轴之比,讨论其特殊螺纹密封面上的应力分布情况。根据试算结果,母接头密封面的内锥角θ=3.6°,公接头椭圆密封结构的短半轴b=0.1 mm。假设密封面椭圆长半轴在1.5~4.5 mm之间变化,即椭圆的短半轴与长半轴之比分别为1/15,1/20,1/25,1/30,1/35以及1/40。
图9示出特殊螺纹扣球面对锥面椭圆密封结构,在不同椭圆率下密封接头上vonMises应力分布云图。可以看出,特殊螺纹接头密封结构的最大vonMises应力出现在椭圆密封面接触位置以及接头内台肩位置,并且整个特殊螺纹接头密封结构的应力处于弹性应变阶段,而且随着椭圆长半轴b的增大,整个密封结构的vonMises应力呈现减小趋势。
图10示出不同椭圆率下,特殊螺纹密封面上接触应力分布曲线。可以看出,随着椭圆密封面长半轴的增加,特殊螺纹接头最大接触应力在逐渐减小,而接触面上的接触宽度在逐渐增大。还可以看出,在椭圆率为1/15~1/40范围内变化时,特殊螺纹密封接触压力均能满足密封要求(气密封压力大于150 MPa)。
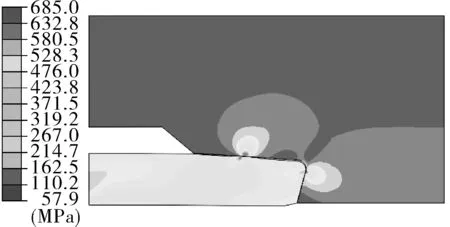
(a)椭圆率1/15

(b)椭圆率1/20

(c)椭圆率1/25

(d)椭圆率1/30

(e)椭圆率1/35
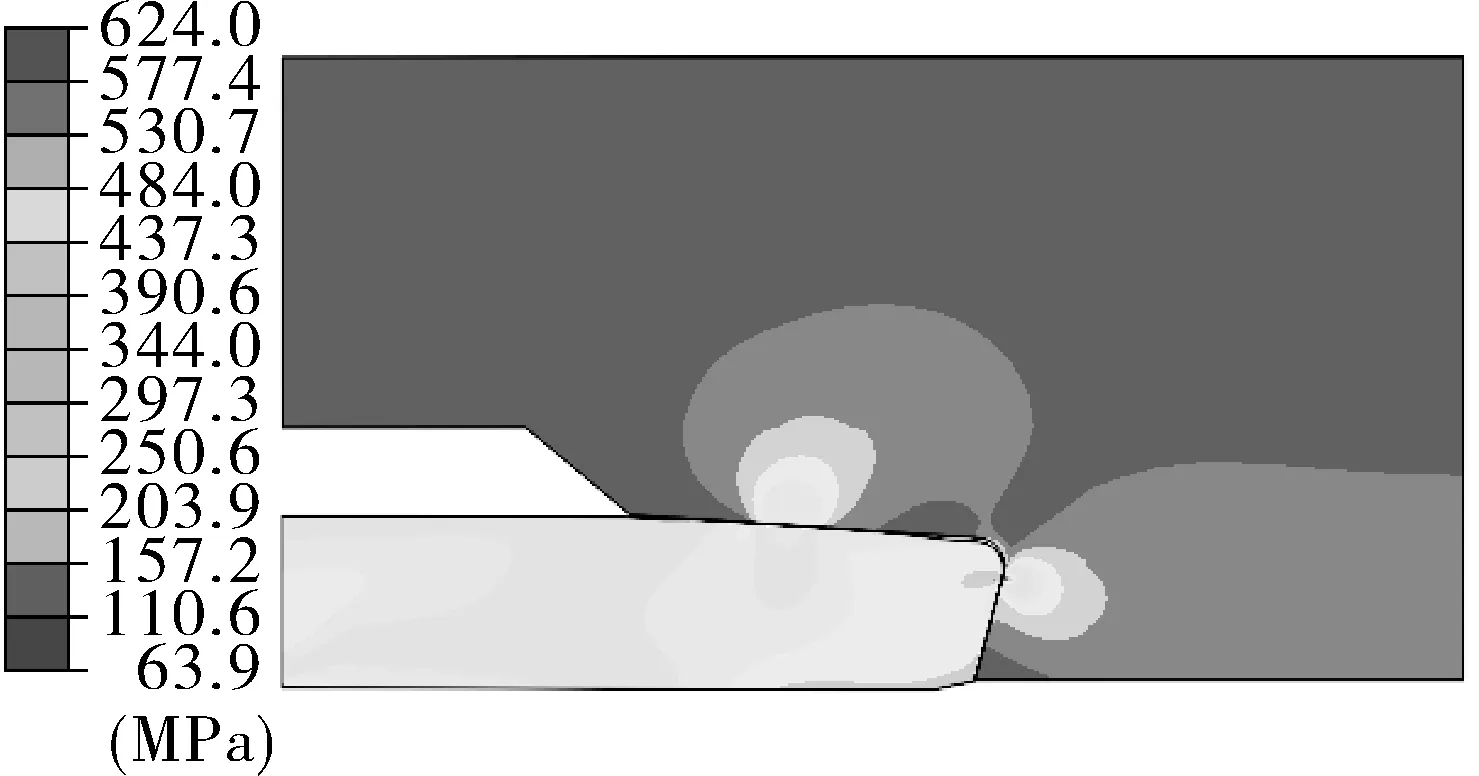
(f)椭圆率1/40

图10 不同椭圆率下特殊螺纹密封面上接触应力分布曲线
2.3 密封接触能判据
密封接触能机理认为,阻止气体通过金属对金属密封结构的流动阻力可由密封接触强度fs表征,它定义为密封接触应力在有效密封长度上的积分值[22]。
(4)
式中fs——密封接触强度,MPa·mm;
L——有效密封接触长度,mm;
PsN——密封面接触应力,MPa。
根据式(4),可以对图10特殊螺纹接头密封面上接触应力在接触路径上的积分,得到接触应力分布曲线所围成的面积,即为该椭圆率下特殊螺纹接头密封结构的密封接触能,其计算结果如图11所示。可以看出,当椭圆密封结构长半轴在1.5~3.5 mm之间变化时,即密封面的椭圆率在1/15~1/35范围内,密封接触能的变化并不明显,而随着椭圆密封结构长半轴的继续增加,密封接触能呈现明显的下降趋势。因此,特殊螺纹球面对锥面的椭圆密封结构的椭圆率取值范围推荐为1/15~1/35。但随着椭圆密封结构长半轴的增加,密封面上的最大接触应力随之下降,密封接触长度随之上升,应力集中现象也在逐步减弱。因此,在特殊螺纹球面对锥面椭圆密封面结构设计时,特殊螺纹球面对锥面的椭圆密封结构的椭圆率的最佳取值范围为1/25~1/35。
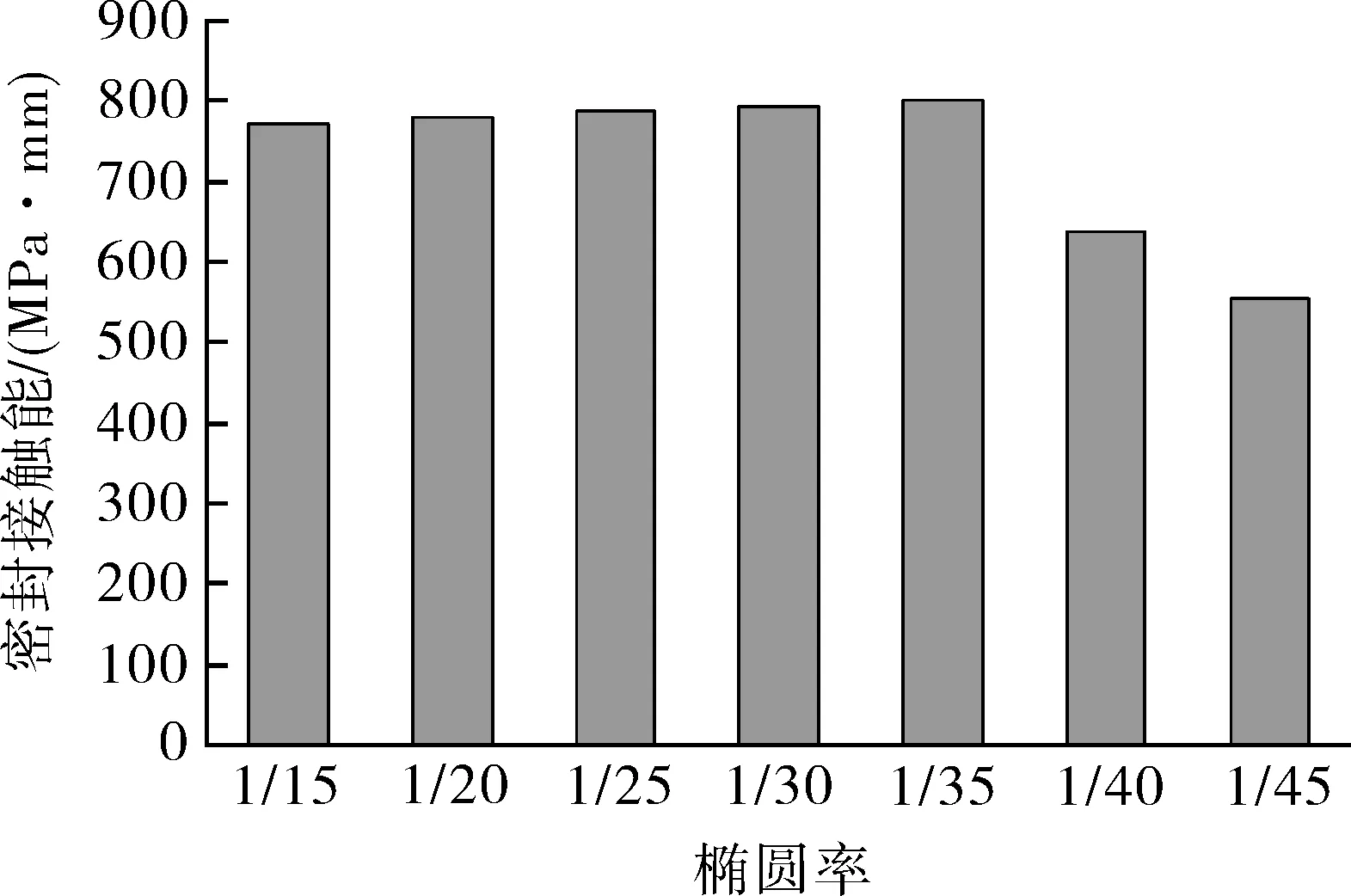
图11 不同椭圆率下特殊螺纹密封面的密封接触能
3 结论及建议
(1)建立了特殊螺纹锥面对锥面密封结构的数值仿真模型。研究发现,特殊螺纹等锥面密封结构存在密封接触不协调现象,即在特殊螺纹等锥接触密封面上沿路径AB的接触压力分布呈两头大、中间小的特点。且在密封面上A位置点接触应力最大;在密封面B位置点接触应力水平较低。而密封面上B位置点正好是密封泄漏的起始点,应设法提高B位置点接触应力。
(2)非等锥线性接触密封结构能够有效改善特殊螺纹密封面上接触不协调现象,改善特殊螺纹密封面上的应力分布。建议在特殊螺纹扣锥面线性接触式密封结构中,其接头密封面结构采用非等锥线性接触密封结构,且母接头密封面内锥角应该大于公接头密封面内锥角5%~8.5%。
(3)针对特殊螺纹球面对锥面密封结构设计,椭圆密封球面具有接触宽度大、接触压力高的特点,并且密封面上球面的椭圆率的最佳取值范围为1/25~1/35。

