厚板大型封头9Ni钢高温本构方程构建

黄天伦1，魏坤霞1，魏 伟1，郭 强，杜庆柏1，吕向阳

(1.常州大学 材料科学与工程学院 石油和化工行业装备表面工程与新材料重点实验室，江苏常州 213164；2.常州旷达威德机械有限公司 常州市高端异形特材封头工程技术研究中心，江苏常州 213171)

0 引言

压力容器广泛应用于化工、建材、食品、纺织、航天、造纸等工业领域，封头是压力容器的重要承压部件[1-2]。随着世界经济与工业生产的迅猛发展，以及国家对环境问题的越来越重视，人们对清洁能源——液化天然气(Liquified Natural Gas，简称LNG)的需求量越来越大[3-5]，国内外建造大型LNG设备和压力容器的需求也随之不断增加，并且对其安全性要求也越来越高，对大型厚壁封头的成型精度要求也相应提高。目前，建造大型低温储罐和压力容器的主要用材是低温韧性优良的9Ni钢[6]。9Ni钢是Ni质量分数为8.5%～9.5%的铁素体型超低温用钢，是LNG工程中一种非常关键的低温材料，其直接与冷冻的液化天然气接触，主要用作于液化天然气储罐、船以及其他配套设施的内部结构材料，具有较高的强度和良好的超低温韧性[7]。9Ni钢厚板大型封头(厚度≥20 mm，直径≥2 500 mm)是液化天然气罐中最重要的部件之一，也是成型加工过程中最困难的部分。采用有限元数值模拟可以预测金属热成形过程的成形力、验证模具及工艺设计、可能出现的缺陷，并且数值模拟的精度主要取决于模拟过程中使用的材料高温本构模型，因此建立精确的高温本构模型对材料成形加工具有重要意义[8]。本文通过厚板9Ni钢的热压缩试验，在不同温度、不同应变速率的情况下，采用双曲正弦形式的Arrhenius公式构建厚板9Ni钢的高温本构模型。

1 试验材料及方法

试验采用9Ni钢，材料各元素的质量分数如表1所示。试样经锻造后，切割成∅8 mm×15 mm的圆棒。在Gleeble-3500热模拟实验机上进行单道次等温热压缩。由于9Ni钢的硬度相对较高，为了避免工件出现开裂、褶皱等缺陷，所以通常采用2～4 mm/s的冲压速度。试样的应变速率分别为0.133 3,0.2和0.266 7 s-1，变形温度分别为770,790,810,830 ℃。将试样以10 ℃/s的速度加热至850 ℃保温5 min，消除内部温度梯度后开始压缩，压下量为80%。

表1 9Ni钢主要化学成分 %

2 试验结果

2.1 高温应力应变曲线测定

通过热压缩试验得到力、位移、温度及时间等数据，绘制出9Ni钢在不同应变速率下的真应力-真应变曲线。图1为该材料在变形温度为770～830 ℃，应变速率为0.133 3～0.266 7 s-1条件下的真应力-真应变曲线。应力随着变形温度的增大而减小，随着应变速率的增大而增大。在同一应变速率的条件下，应力先迅速增加到峰值，然后曲线略微下降并趋于饱和，出现这种现象的原因是在变形的过程中发生动态再结晶或动态回复导致的材料软化[9]。

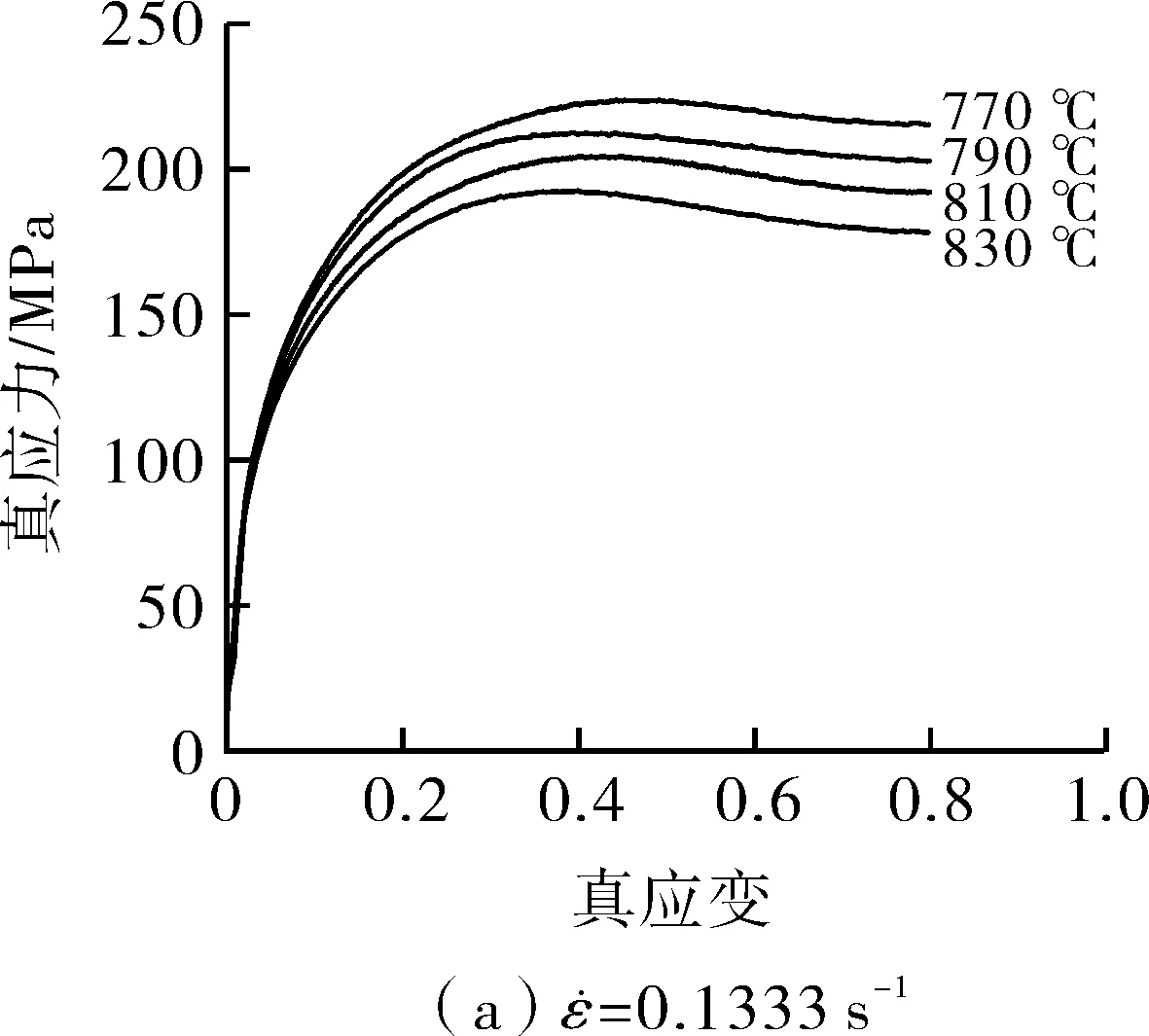
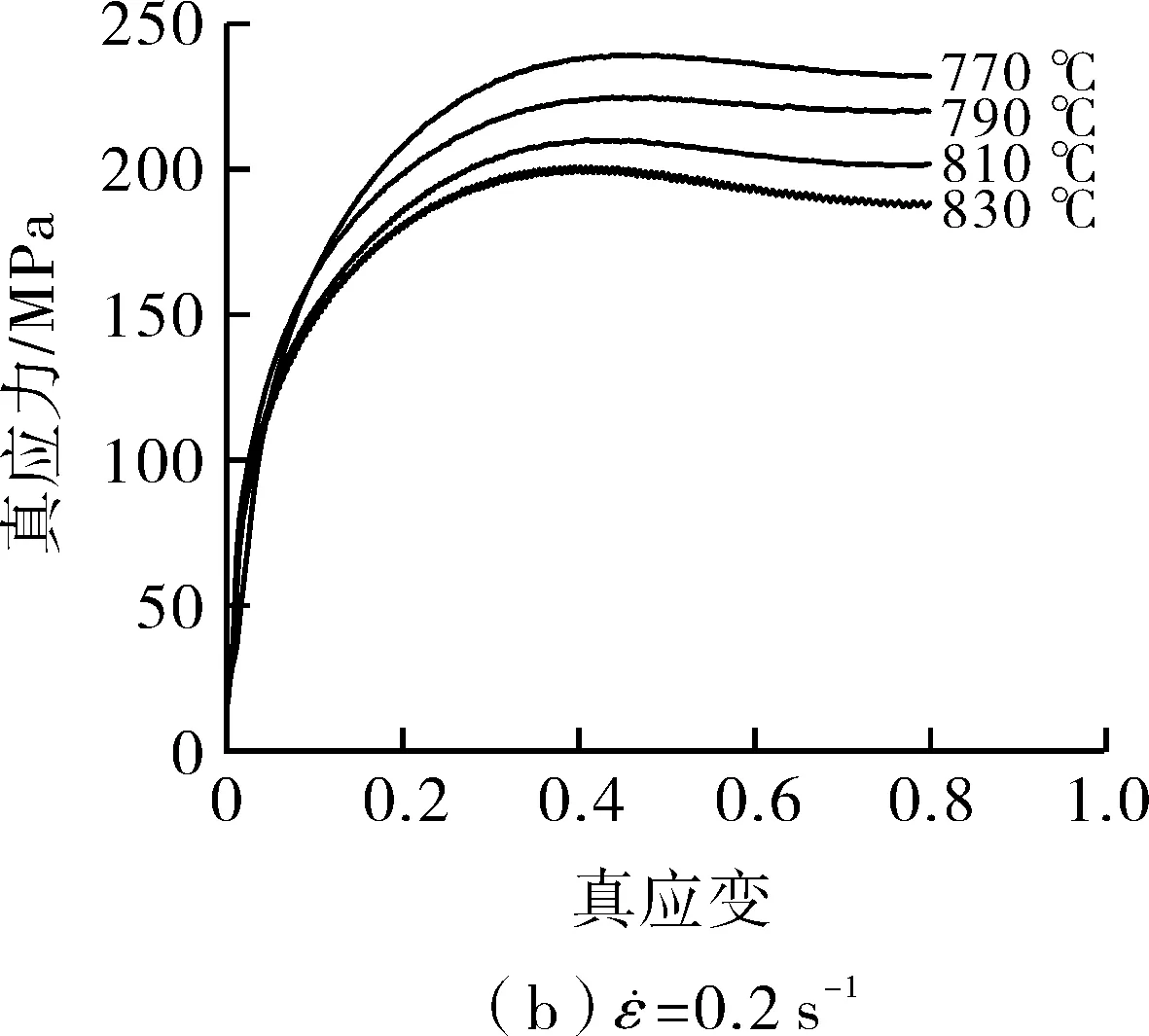
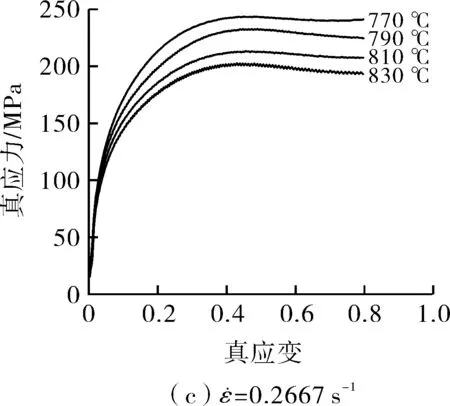
图1 9Ni钢在不同应变速率下的高温真应力-真应变曲线

2.2 9Ni钢高温本构模型构建

(1)

(2)

(3)

σ——真应力，MPa;

Q——材料的变形激活能，kJ/mol;

R——摩尔气体常数，J/(mol·K);

T——变形温度，K;

n,n1,α,β,A,A1,A2——取决于材料的参数，其中α=β/n1。

在这项试验中，研究了应变速率对9Ni钢高温本构方程材料参数的影响。下面以应变ε=0.4为例，介绍材料参数的计算过程。

式(2),(3)分别为低应力水平(ασ<0.8)和高应力水平(ασ>1.2)的Arrhenius公式，分别将其两边取对数可得：

(4)

(5)

将在ε=0.4时的流动应力和相应的应变速率的值代入式(4)和(5)，得到流动应力和应变速率之间的关系，并采用最小二乘法进行线性回归，如图2所示。由于线的斜率大致相同，因此可以通过计算平均值获得不同变形温度下的n1和β的值，分别为10.848 34和0.049 66。通过α=β/n1可求得，α=0.004 58。

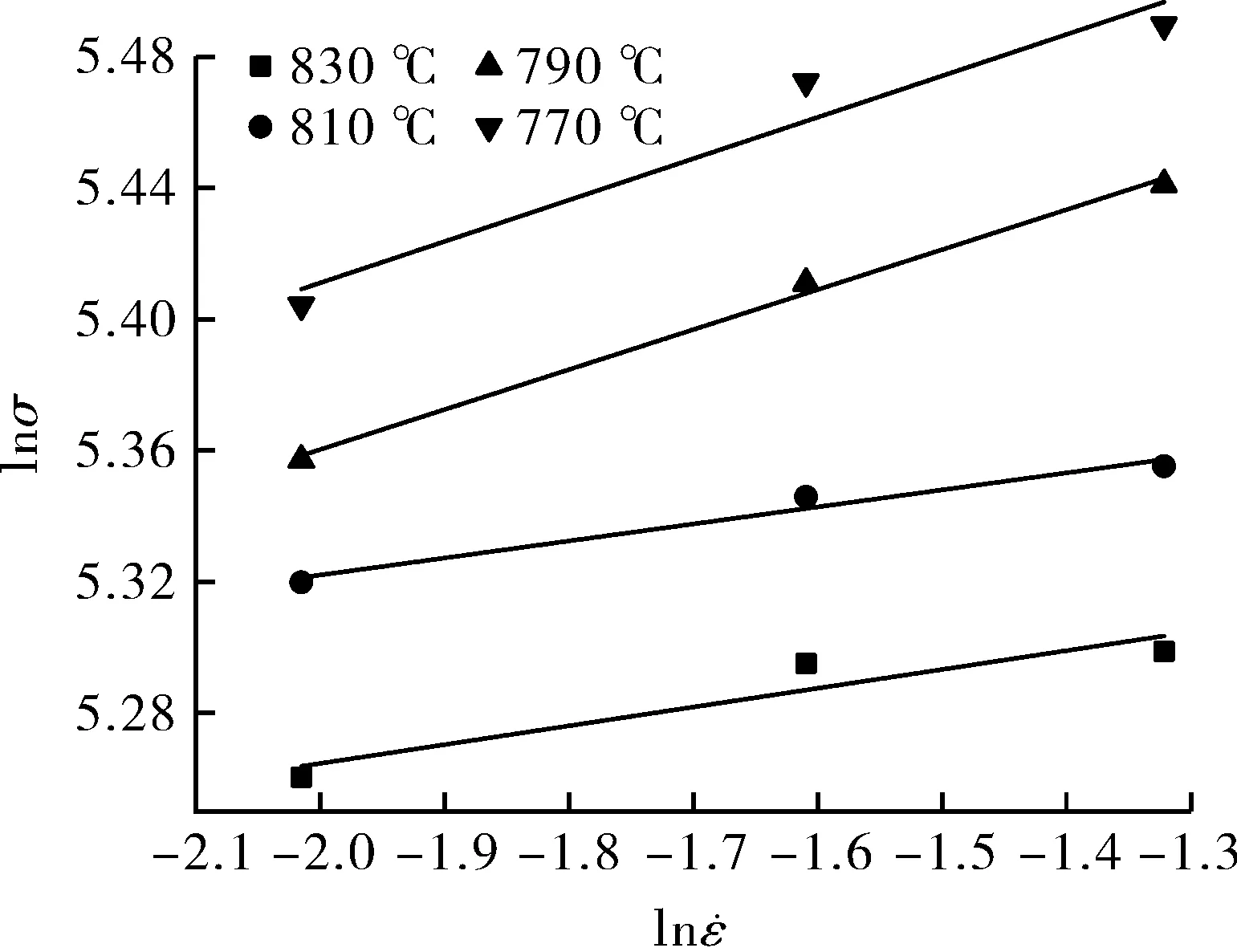
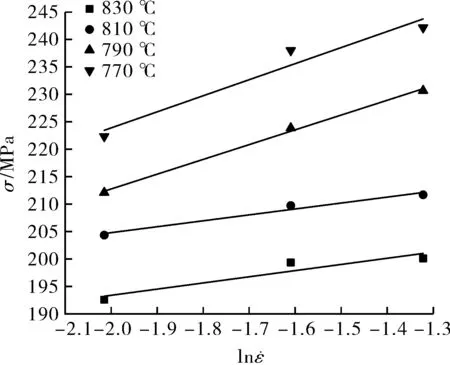
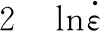
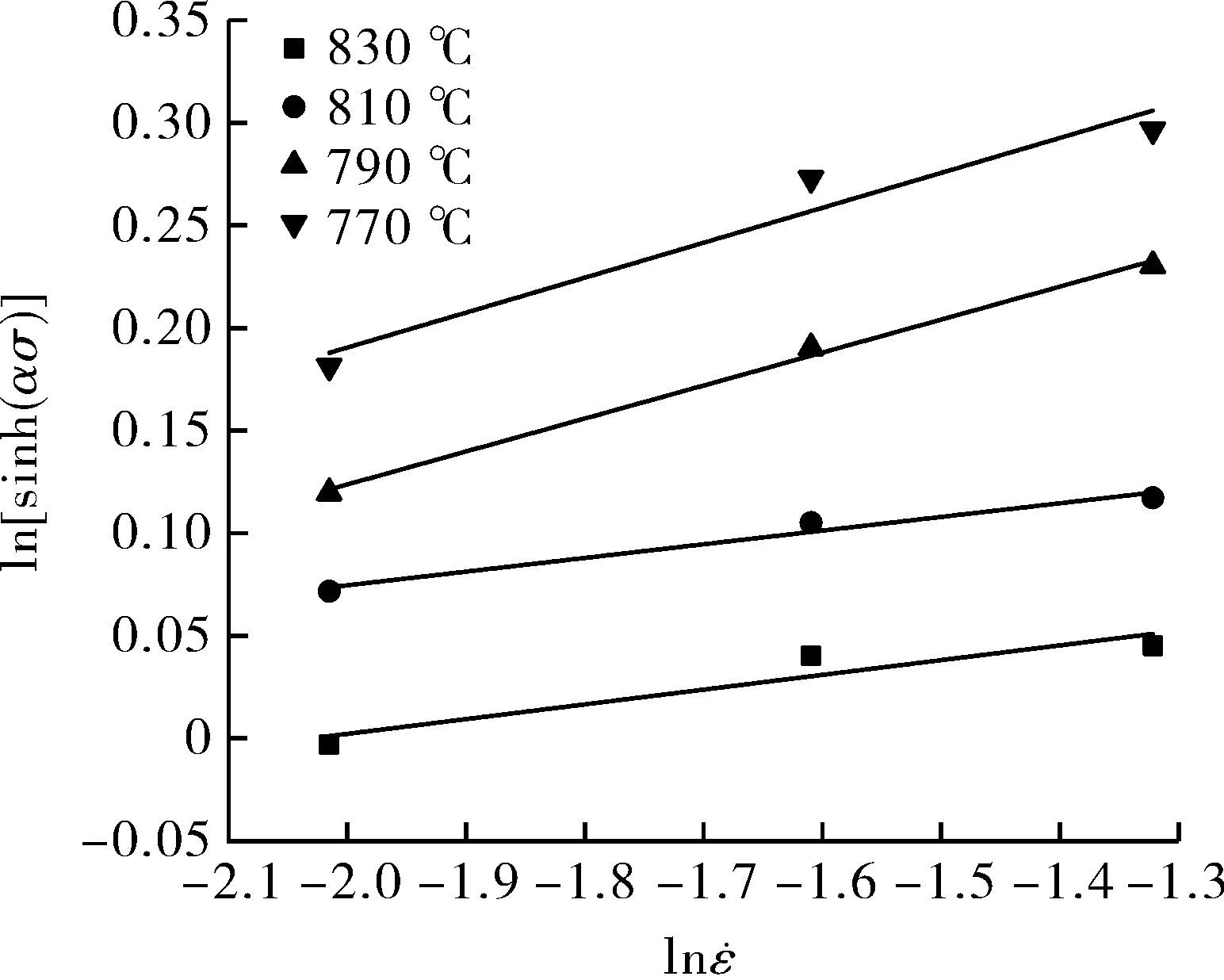
图3 ln[sinh(ασ)]和之间的关系(ε=0.4)

对于所有的应力水平(包括低和高应力水平)的Arrhenius公式，通过式(1)两边取对数变形可得：

(6)

温度和应变速率对变形行为的影响可以用指数形式的Zener-Hollomon参数表示[10]：

(7)

通过双曲线定律，可以将式(6)的流动应力σ写成包含Zener-Hollomon参数的函数：

(8)

(9)

将式(7)求偏导可得：

(10)

因此，将在ε=0.4时的流动应力和相应的应变速率值代入式(10)。Q可从ln[sinh(ασ)]-1/T的函数曲线中的斜率导出，如图4所示。由于线的斜率大致相同，因此可通过计算平均值获得不同变形温度下的Q值，Q=289.131 42 kJ/mol。

图5 sinh(ασ)]和lnZ之间的关系

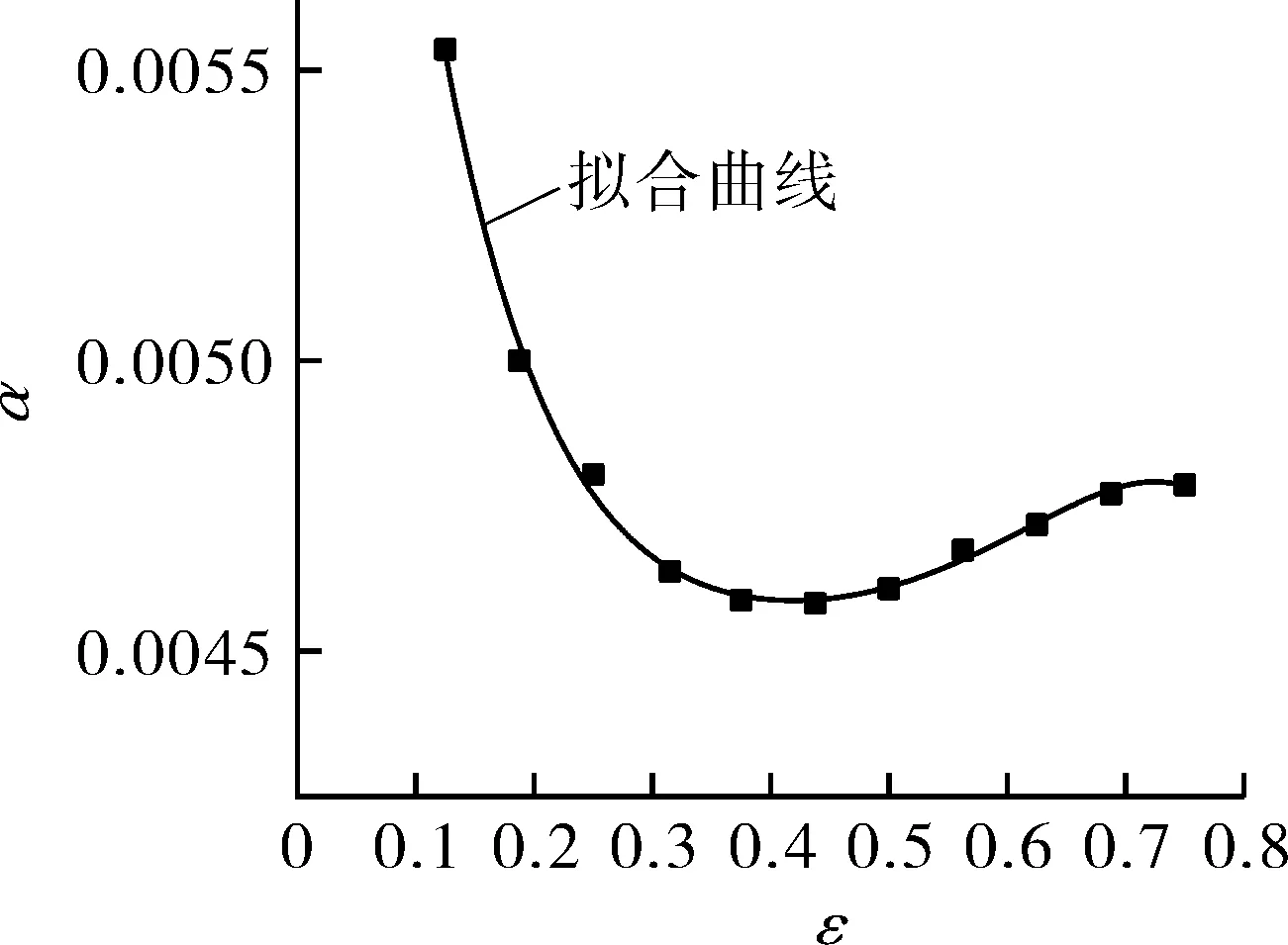
(a)α-ε

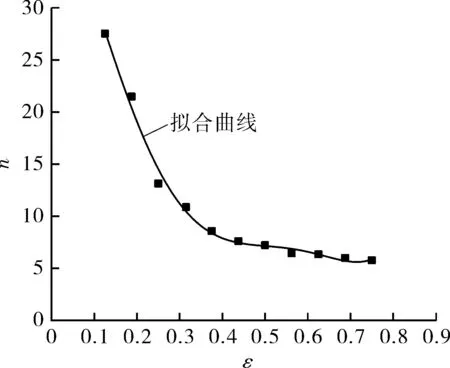
(b)n-ε

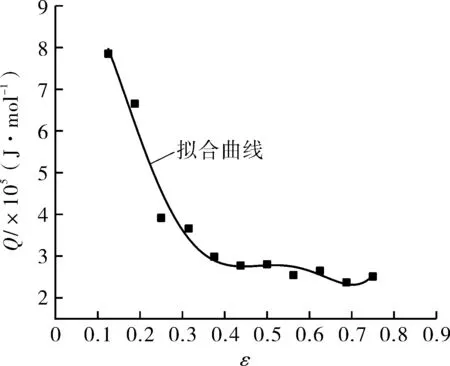
(c)Q-ε

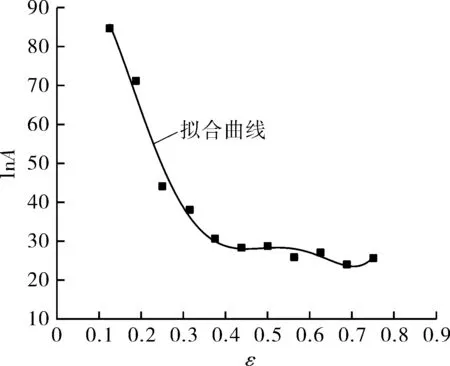
(d)lnA-ε

图6 多项式拟合α,n,Q,lnA和应变ε之间关系

将在ε=0.4时的流动应力和相应的应变速率值代入式(8)。可得到ln[sinh(ασ)]和lnZ之间的关系，如图5所示。从该图中，通过截距可以算出lnA的值，lnA=29.582 48。

然后在ε=0～0.8的范围内,计算不同变形应变下的9Ni钢高温本构方程的材料参数(α,n,lnA,Q)的值。图6为9Ni钢的α,n,lnA,Q和真应变之间的关系,可以通过应变补偿进行多项式拟合，如式(11)～(14)所示。表2为拟合所获得的多项式系数[11-14]。

α=B0+B1ε+B2ε2+B3ε3+B4ε4+B5ε5

(11)

n=C0+C1ε+C2ε2+C3ε3+C4ε4+C5ε5

(12)

Q=D0+D1ε+D2ε2+D3ε3+D4ε4+D5ε5

(13)

lnA=E0+E1ε+E2ε2+E3ε3+E4ε4+E5ε5

(14)

表2 多项式拟合α,n,Q,lnA的系数

2.3 9Ni钢高温本构模型验证

图7为应变速率0.133 3,0.2,0.266 7 s-1时，9Ni钢在4种不同温度下的本构方程的试验和预测结果之间的比较，能够观察出模型预测结果与试验结果吻合得较好。为了评估变形本构方程的精度，计算的流动应力和测量的流动应力之间的误差可以通过式(15)和式(16)表示的相关系数R1和平均相对误差AARE来检验由模型式(9)预测真应力的准确程度[12]。分别从试验结果和模型预测结果的真应力曲线上等间距取若干个点用于计算R1和AARE，计算结果分别为0.969和6.18%。图8为试验真应力和模型预测结果的相关性。由此可知，高温本构模型可以较好地预测出9Ni钢的真应力并能满足数值模拟的精度要求。

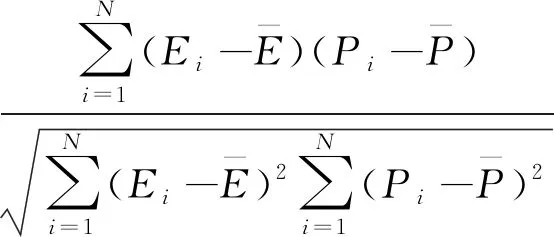
(15)

(16)

式中Ei——试验真应力，MPa；

Pi——模型预测真应力，MPa；

N——选取数据点的数量。

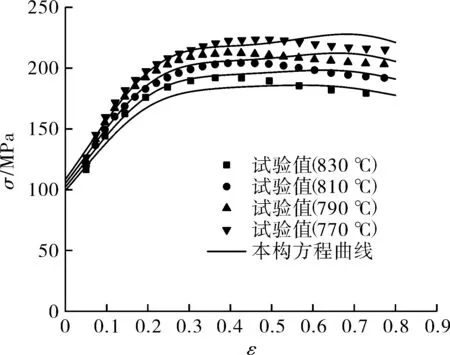
(a)应变速率0.133 3 s-1

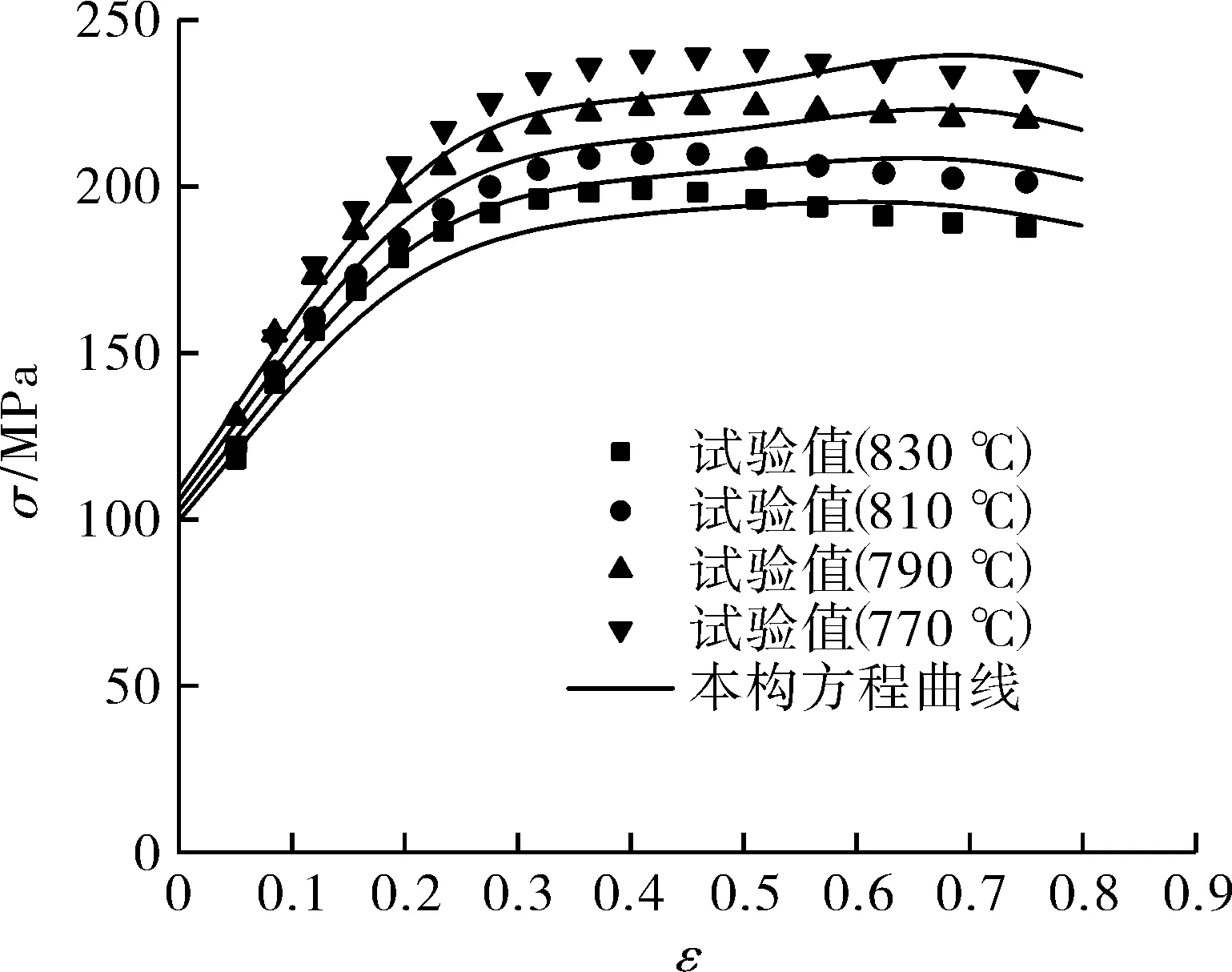
(b)应变速率0.2 s-1

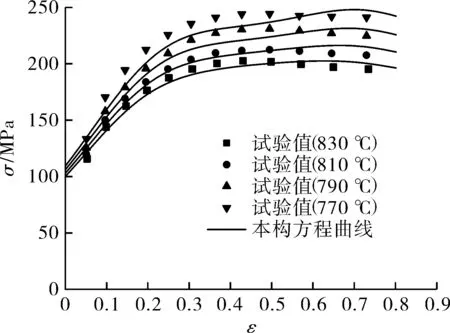
(c)应变速率0.266 7 s-1

将本构方程式(9)应用到DEFORM-3D材料库中，采用Solidworks进行三维实体建模，并将其转化为*.stl文件，然后导入到DEFORM-3D软件中，进行预冷冲压，压下高度520 mm，如图9所示。凸模、凹模和压边圈设置为刚体，材料为AISI-H-13。9Ni钢的塑性变形温度通常在800～850 ℃[15],厚板9Ni钢DEFORM-3D热冲压模拟的相关参数如表3所示。计算过程中未出现网格畸变或网格重划分，且一次完成。

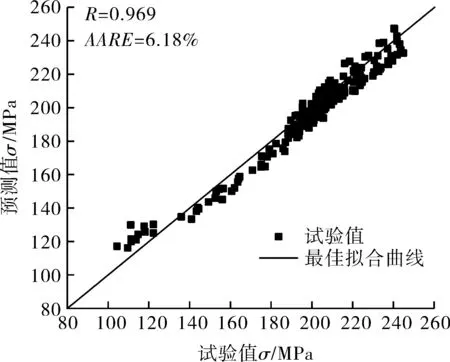
图8 试验真应力和模型预测结果的相关性

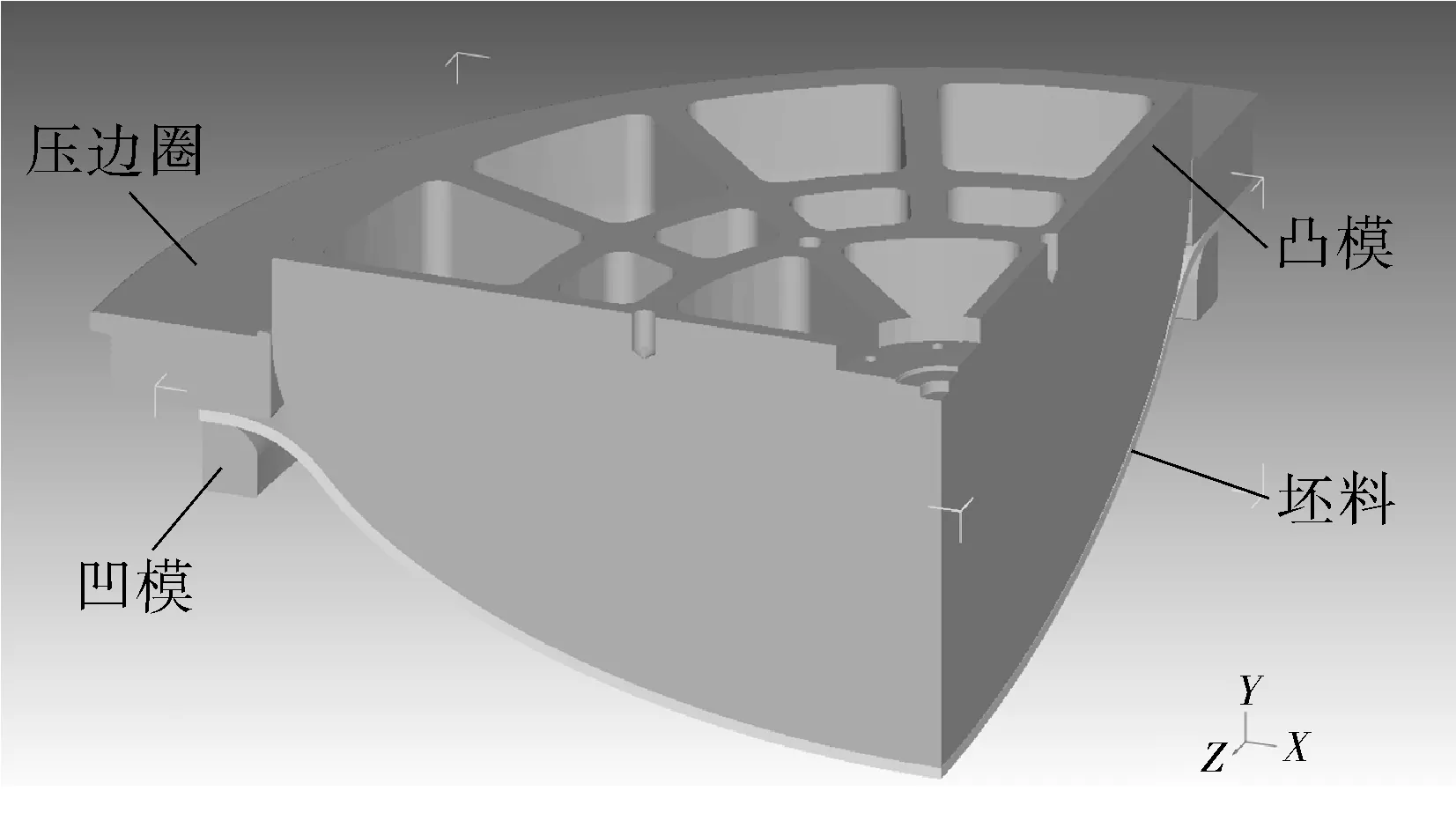
图9 9Ni钢厚板大型封头有限元模拟1/4模型

表3 厚板9Ni钢DEFORM-3D热冲压模拟参数

图10为模拟计算结果。从应力云图和应变云图可以看到，锻件变形主要集中在压边圈向下模转动区域，这是因为封头已经过一次预冷冲压，封头底部与下模已完全贴合。9Ni钢封头整个成形过程未发现开裂、褶皱等缺陷，与实际生产结果相吻合(见图11)。因此该本构方程适用于9Ni钢厚板大型封头成形加工过程的模拟分析。

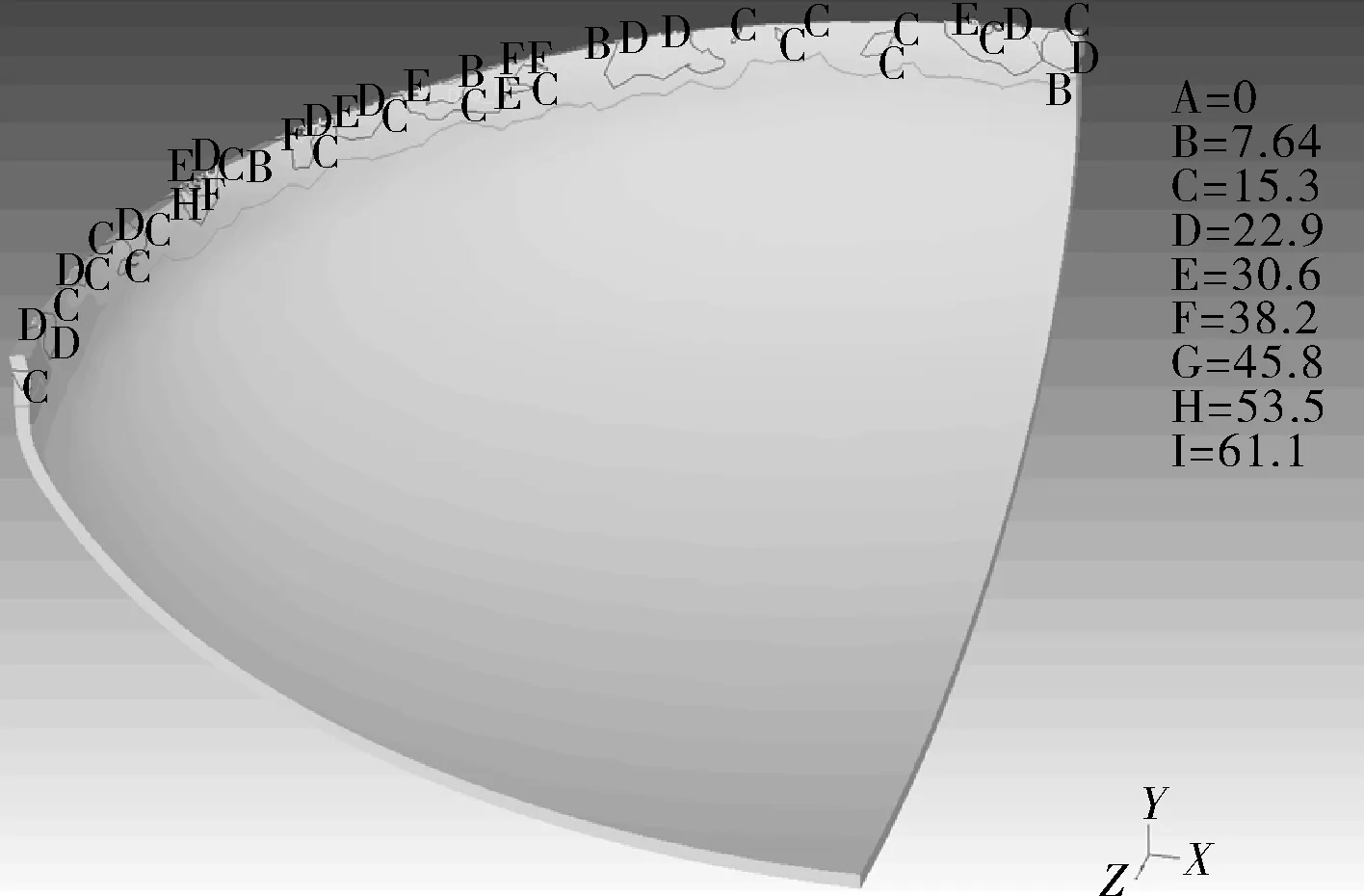
(a)等效应力云图

(b)等效应变云图

图10 9Ni钢厚板大型封头锻件1/4模型模拟结果

图11 9Ni钢厚板大型封头实物图

3 结论

(1)采用双曲正弦形式的Arrhenius方程，多项式拟合将材料参数表示成关于应变的函数，构建了厚板9Ni钢的高温本构模型。

(2)试验真应力和模型预测结果的相关性系数R1和平均相对误差AARE分别为0.969和6.18%，表明本文建立的厚板9Ni钢高温本构模型预测结果与试验值相吻合。该方程形式简单、精度较高、参数易获取，可用于9Ni钢厚板大型封头成形加工过程中的数值模拟与分析。

(3)采用9Ni钢高温本构模型进行Deform-3D模拟计算，工件均未出现开裂褶皱等工艺缺陷，与实际生产工件一致，说明该本构方程能够在模拟计算中较好地反映实际工件的变形状态。