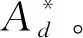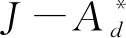材料拘束相关的J-R阻力曲线的构建

(华东理工大学 承压系统与安全教育部重点实验室,上海 200237)

0 引言

材料的延性裂纹扩展阻力通常用J-R阻力曲线来表征，它是裂纹扩展量与裂纹扩展阻力(J积分)之间关系的曲线。J-R阻力曲线通常用于结构(如压力容器、管道等)的延性撕裂及裂纹扩展稳定性评定。在结构延性裂纹起裂和扩展之后，其承载能力还有不同程度的增加，基于J-R曲线的延性撕裂评定可更准确地反映结构抵抗断裂的能力。材料的J-R阻力曲线通常按试验标准(如ASTM E1820[1])用深裂纹高拘束平面应变试样(如单边裂纹弯曲(SEN(B))试样和紧凑拉伸(C(T))试样)测定。然而，许多试验表明，材料的J-R阻力曲线受试样几何、裂纹尺寸和加载方式等的影响[2-3]，即受裂尖拘束水平的影响。如用标准试验方法中的高拘束平面应变试样测得的J-R阻力曲线评定含低拘束裂纹结构(如压力容器、管道中的表面浅裂纹)的安全性,将得到过于保守的结果；如果结构中裂纹的裂尖拘束高于实验室标准试样，则可能得到非保守的评定结果[4]。因此，为了进行准确的结构完整性分析和评定，需要考虑拘束对材料J-R阻力曲线的影响。为此需要基于含拘束效应的二参数断裂力学理论，建立材料J-R阻力曲线与拘束参数的定量关联式，即构建材料拘束相关的J-R阻力曲线，以实现纳入拘束效应的结构完整性分析和评定。

目前，包含拘束效应的二参数断裂力学理论主要包括：J-T[5]，J-Q[6-7]，J-A2[8]和J-Tz[9]等理论。这些理论中基于裂尖应力场的T，Q和A2拘束参数主要用于表征面内拘束，Tz用于表征面外拘束，但它们不能同时表征结构中的面内和面外拘束[10-11]。此外，对于大范围屈服下的SEN(B)试样，J-T，J-Q和J-A2理论失去其有效性[12]。而在实际结构中，面内拘束和面外拘束同时存在，且在延性断裂前，裂尖发生大范围屈服，因此需要发展在宽范围载荷条件下(从小范围屈服到大范围屈服)可同时表征面内与面外拘束的统一拘束参数。在研究组前期工作中，已提出了一个基于裂尖前等效塑性应变εp等值线所围面积的统一拘束参数Ap[13]。参数Ap能够表征宽范围载荷下的延性断裂[13-14]和脆性断裂[15-16]条件下的面内与面外复合拘束，并可以与材料断裂韧性建立统一关联。在进一步的研究中[17]，基于J-Ap二参数结合失效评定图法实现了纳入统一拘束的承压管道的断裂评定。然而Ap参数的计算过程和数据处理较为复杂，不便于工程应用。在研究组最近的工作中[18-19]，基于裂尖张开位移(CTOD)研究定义了一个新的面内/面外统一拘束参数Ad,并建立了该参数与材料断裂韧性的统一关联。由于CTOD可以反映裂尖载荷和塑性应变的大小，且在试验及有限元计算中易于测量和确定。因此，Ad参数也许是一个便于工程应用的统一拘束参数。

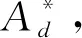
1 有限元计算方法

1.1 材料和试样

以核电压力容器A508钢为研究材料，其室温下的力学性能如表1[13，20]所示，其真应力-应变曲线如图1[13，20]所示。

表1 A508钢室温下的力学性能

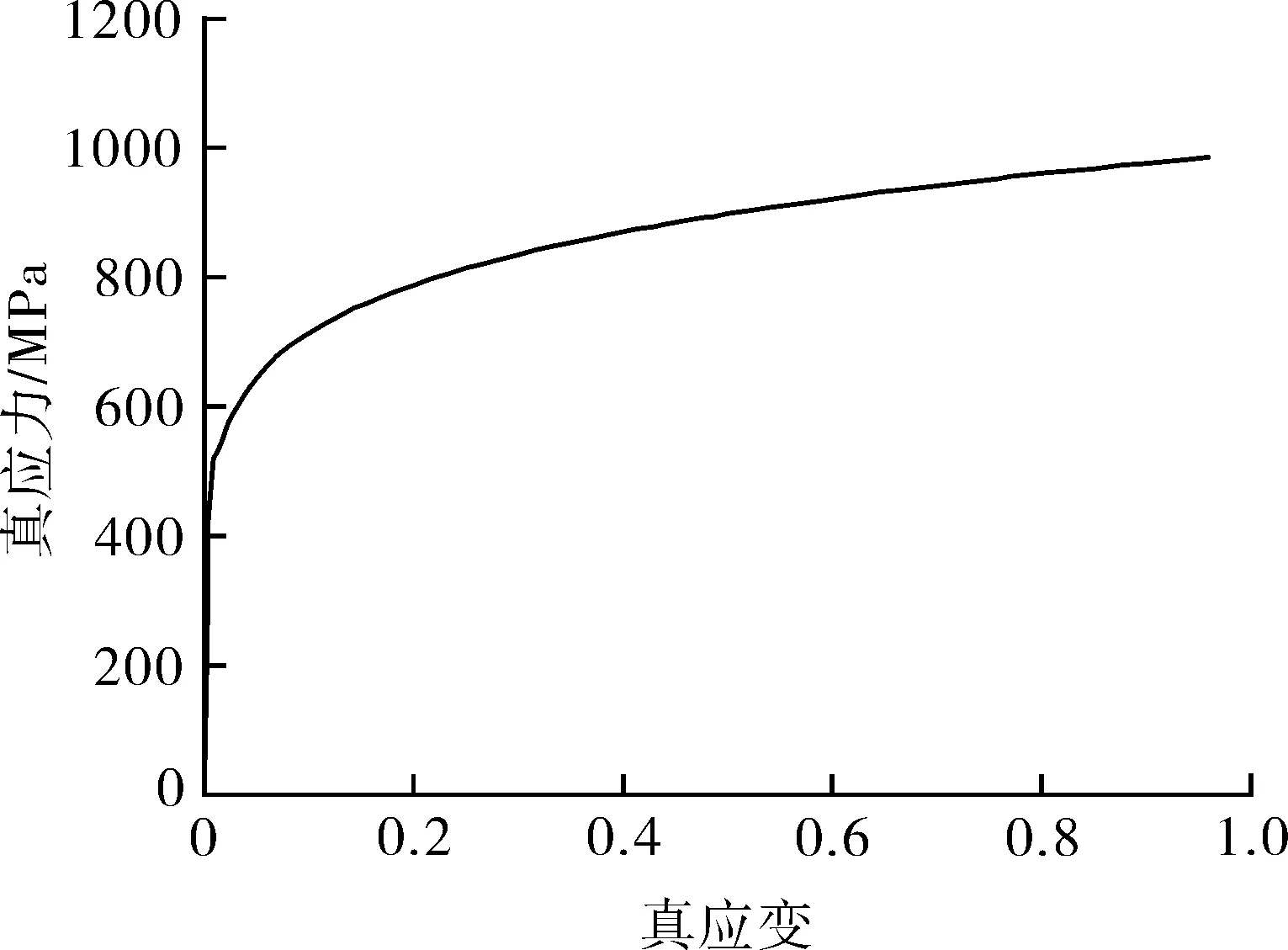
图1 A508钢室温下的真应力-应变曲线

选用研究组前期工作中[20]采用的SEN(B)试样(三点弯曲试样)，其加载方式如图2所示。试样宽度W=32 mm,厚度B=16 mm,加载跨距L=128 mm。通过改变裂纹深度比a/W(a/W= 0.1，0.2，0.25，0.3，0.4，0.5,0.7)以改变试样的拘束水平。

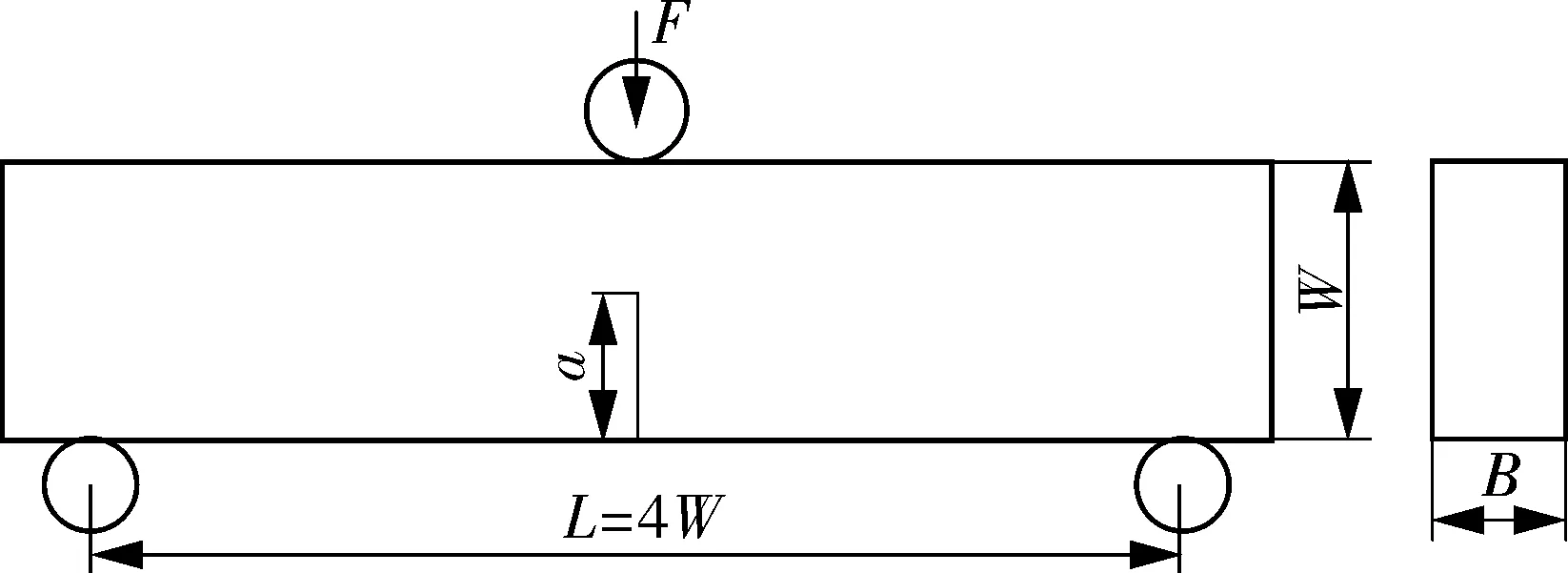
图2 SEN(B)试样的加载方式和尺寸示意

1.2 有限元模型

采用ABAQUS有限元软件[22]对7个不同a/W的SEN(B)试样进行准静态加载时的裂尖J积分和CTOD计算。由于试样的对称性，建立1/2的有限元模型，采用平面应变减缩积分单元CPE4R。试样的加载通过对上方刚体施加向下的位移进行。

为提高计算精度，裂纹尖端划分较细的网格，采用聚焦环式网格包围在初始根半径为2.5 μm的裂纹尖端,以增强非线性迭代计算的收敛性。典型的有限元模型(a/W=0.5，W=32 mm)网格和裂尖附近网格如图3所示。材料的弹塑性参数采用表1中的数据和图1中的真应力-应变曲线数据。

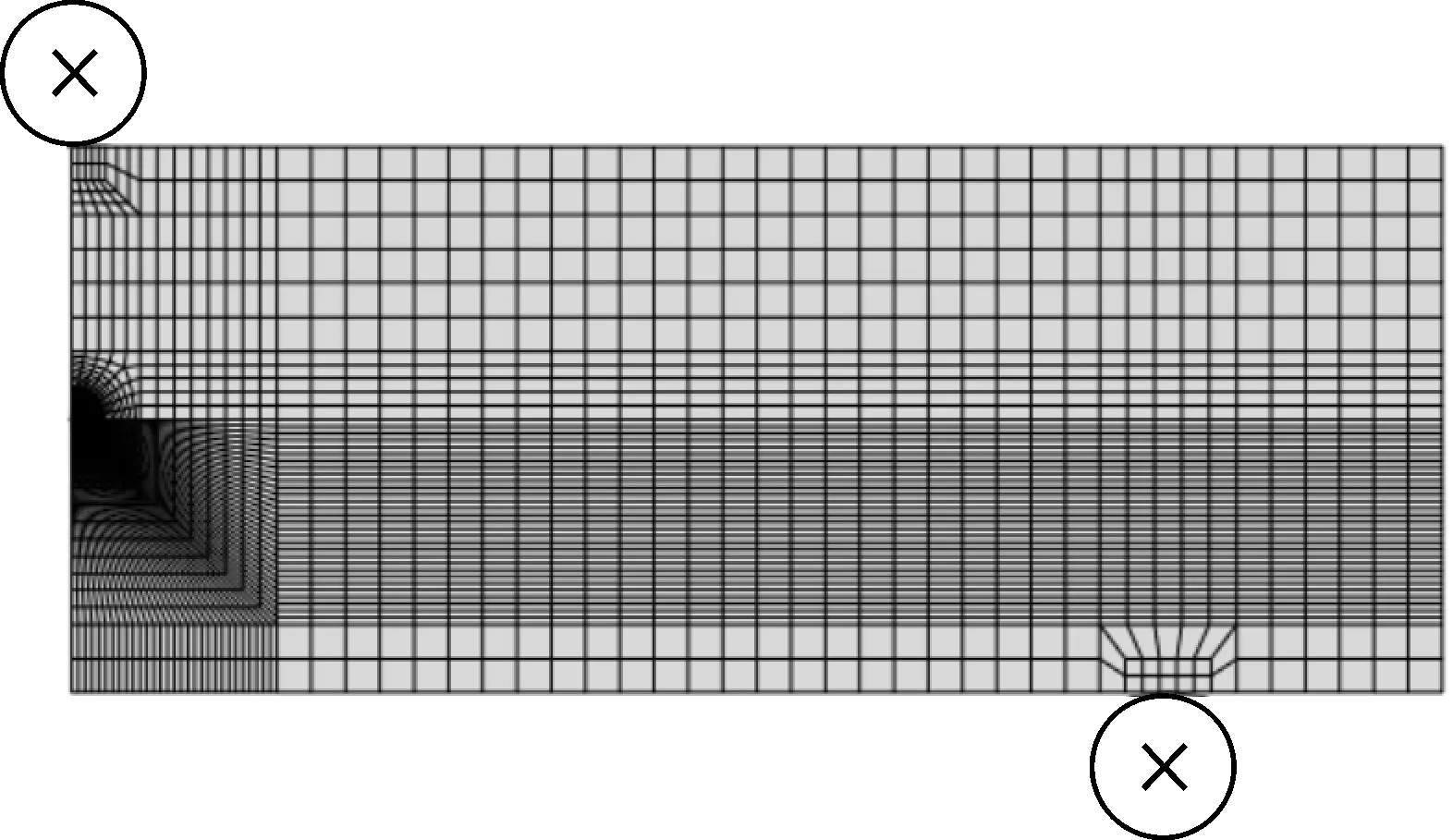
(a)有限元模型网格

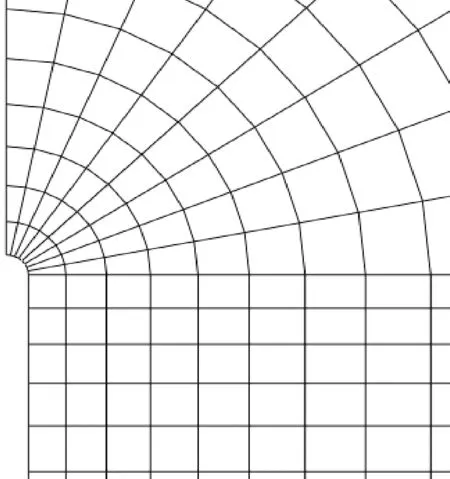
(b)裂尖附近网格

2 载荷无关的统一拘束参数的定义与计算

在延性裂纹起裂和扩展过程中，材料的断裂韧性随裂纹起裂和扩展逐渐变化，而拘束参数通常受外加载荷的影响，在裂纹起裂和扩展中并不能保持为常量。因此在建立拘束相关的J-R阻力曲线中，通常需要定义一个载荷无关的拘束参数[4,20]。研究组前期基于CTOD定义的面内与面外统一拘束表征参数Ad如下[18]：

(1)

式中δ——某一试样或结构裂纹的CTOD值，mm；

δref——标准平面应变参考试样在断裂时的CTOD值，mm。

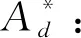
(2)

式中δJ——某一试样或结构在一定J积分(载荷水平)下的CTOD值,mm；

δrefJ——标准平面应变参考试样在同样J积分下的CTOD值,mm。

环境伦理主要是指人与自然之间和谐共生的关系。然而，随着工业文明的发展，人类一味的索取与侵占自然，在满足了各种物质欲望的同时，也面临着精神世界失衡的窘境。人与人之间的和谐关系也遭到了破坏。尼古拉斯认为人类只有尊重、亲近自然，与自然重建和谐关系才能得到救赎。在《勇敢者》中，凯尔与其家人在农场和谐生活的场景以及他最终成为汤米和戴安娜心灵慰藉的事实，成为作者表达他环境伦理观的最好证明。

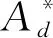
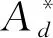
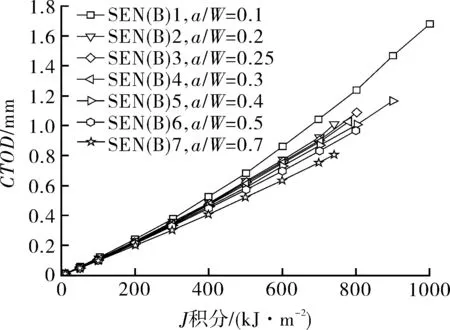
图4 不同拘束SEN(B)试样的CTOD随J积分的变化

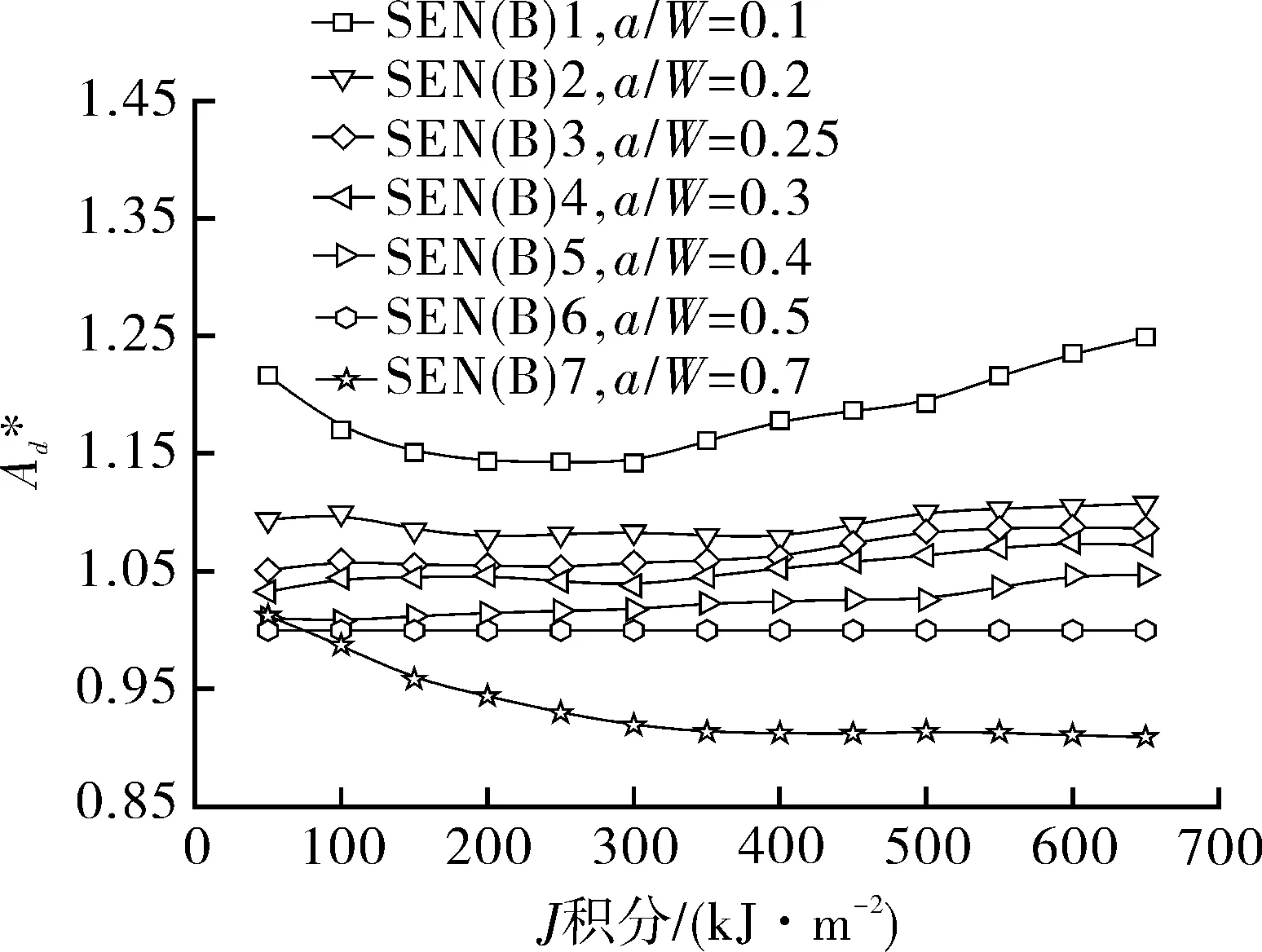
图5 不同拘束SEN(B)试样的拘束参数随J积分的变化

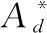
表2 不同a/W试样的载荷无关的拘束参数值

3 拘束相关的J-R阻力曲线的构建

为了构建材料拘束相关的J-R阻力曲线方程，需要使用几个不同拘束试样的J-R曲线。这些J-R曲线可以通过试验测试得到，为降低试验成本，也可通过基于GTN(Gurson-Tvergaard-Needleman)延性损伤模型的数值模拟得到[20]。对于本文不同a/W的7个SEN(B)试样，在前期工作中，已采用基于GTN延性损伤模型的数值模拟得到了其J-R阻力曲线，如图6[20]所示。通过a/W=0.3,0.5，0.7的3条试验曲线与模拟曲线的一致性，验证了有限元模拟的准确性[20]。从图6可以看出，随a/W增加(拘束增大)，J-R阻力曲线降低。

在ASTM E1820[1]标准中，J-R阻力曲线，即J积分与裂纹扩展量Δa之间的关系曲线一般用下式描述：

J(Δa)=C1(Δa)C2

(3)

式中C1，C2——常数，通过曲线拟合得到。

当包含拘束效应时，J-R阻力曲线可用下式描述[4,20-21]：

(4)

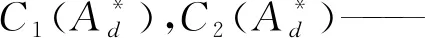
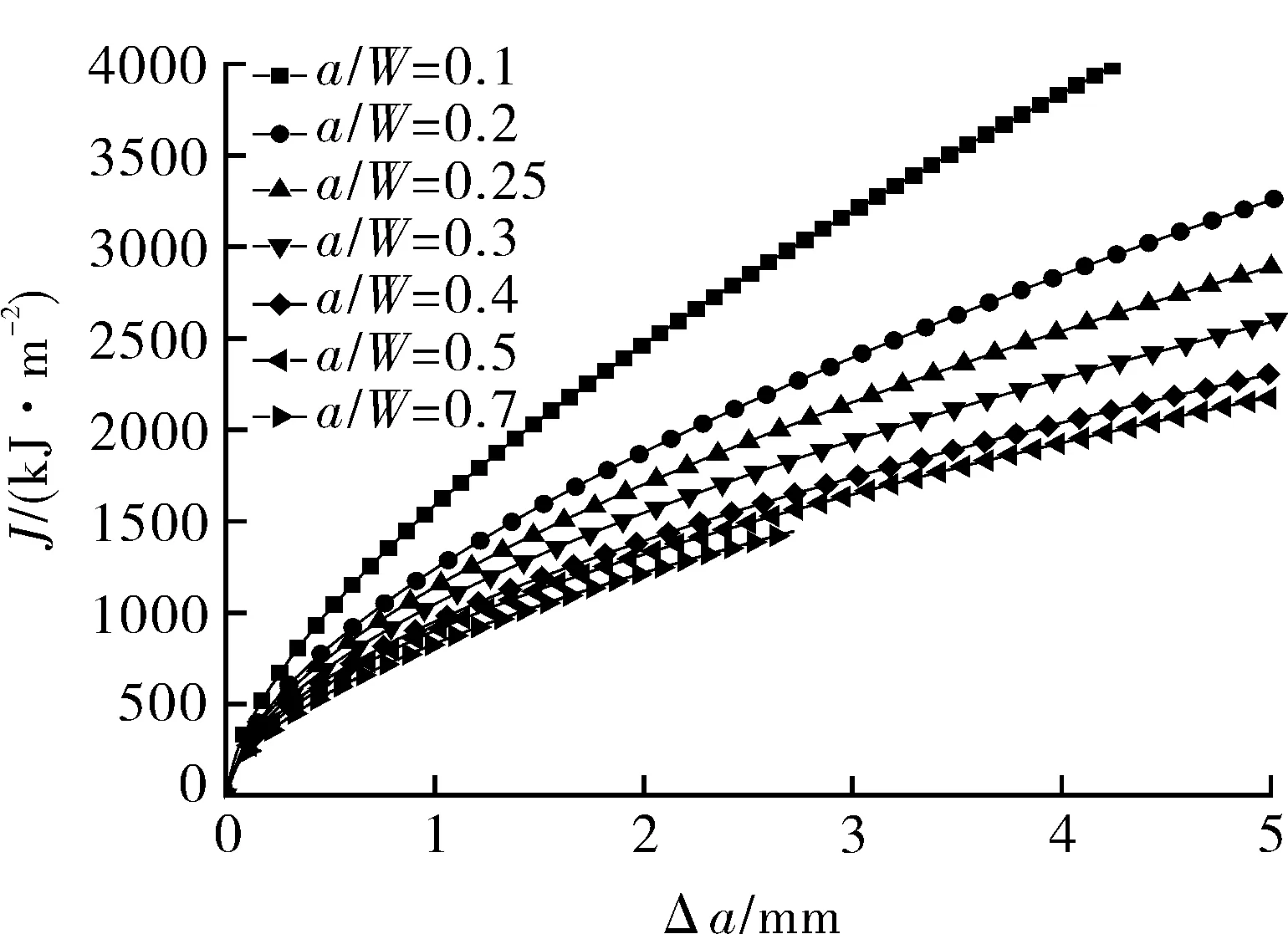
图6 不同拘束的SEN(B)试样的J-R阻力曲线

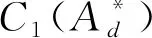
(5)

(6)

(7)

(8)

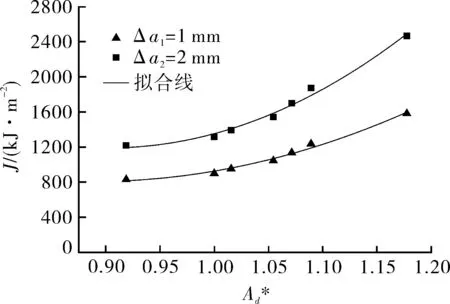
图7 JΔa1=1 mm和JΔa2=2 mm与拘束参数的关系曲线

对图7中的曲线可以拟合为以下两个关系式:

(9)

(10)

(11)

(12)

将式(11)，(12)代入式(4)，即可得到拘束相关的J-R阻力曲线的数学式：

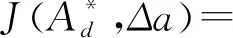
(13)

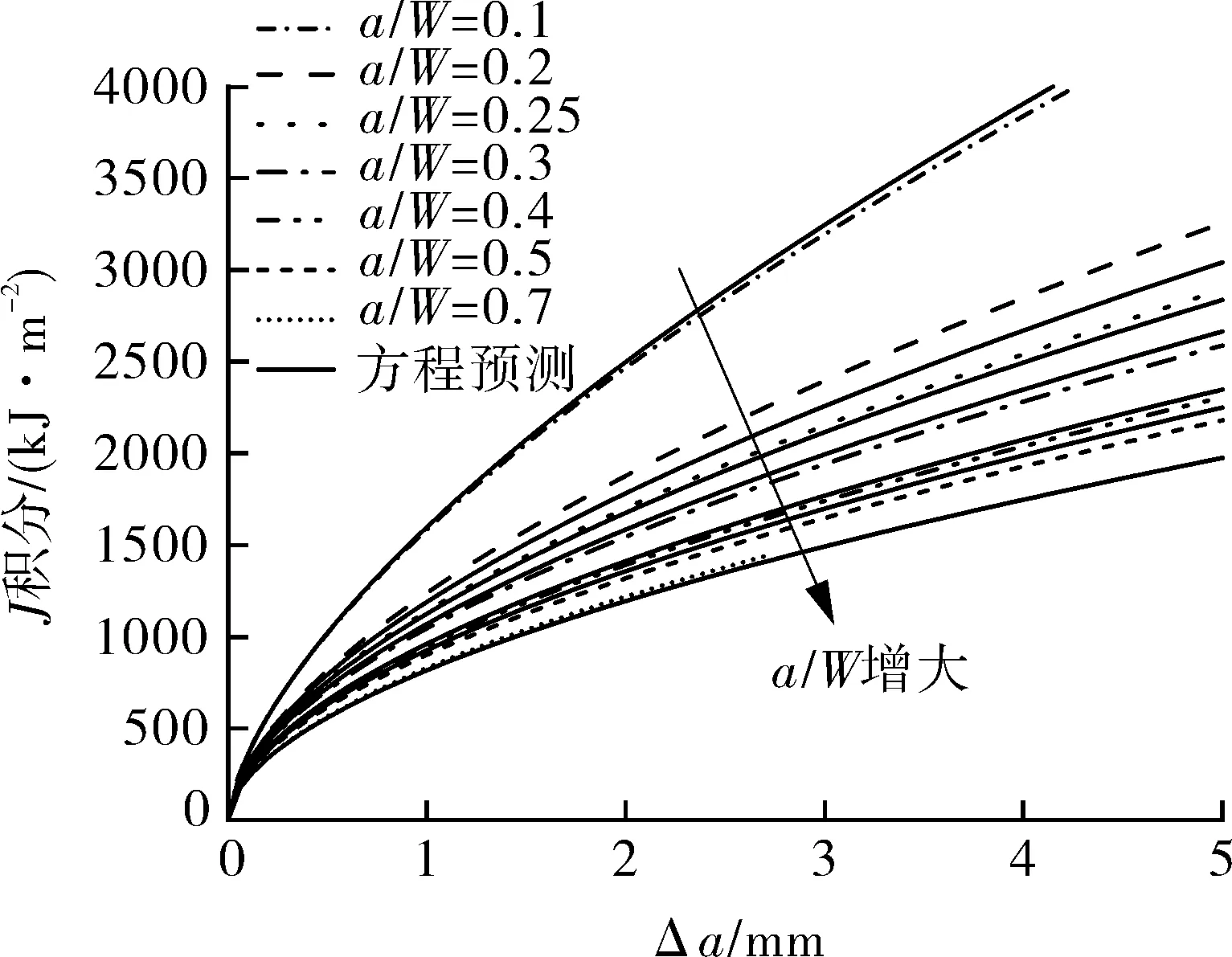
(a)与数值模拟曲线的对比

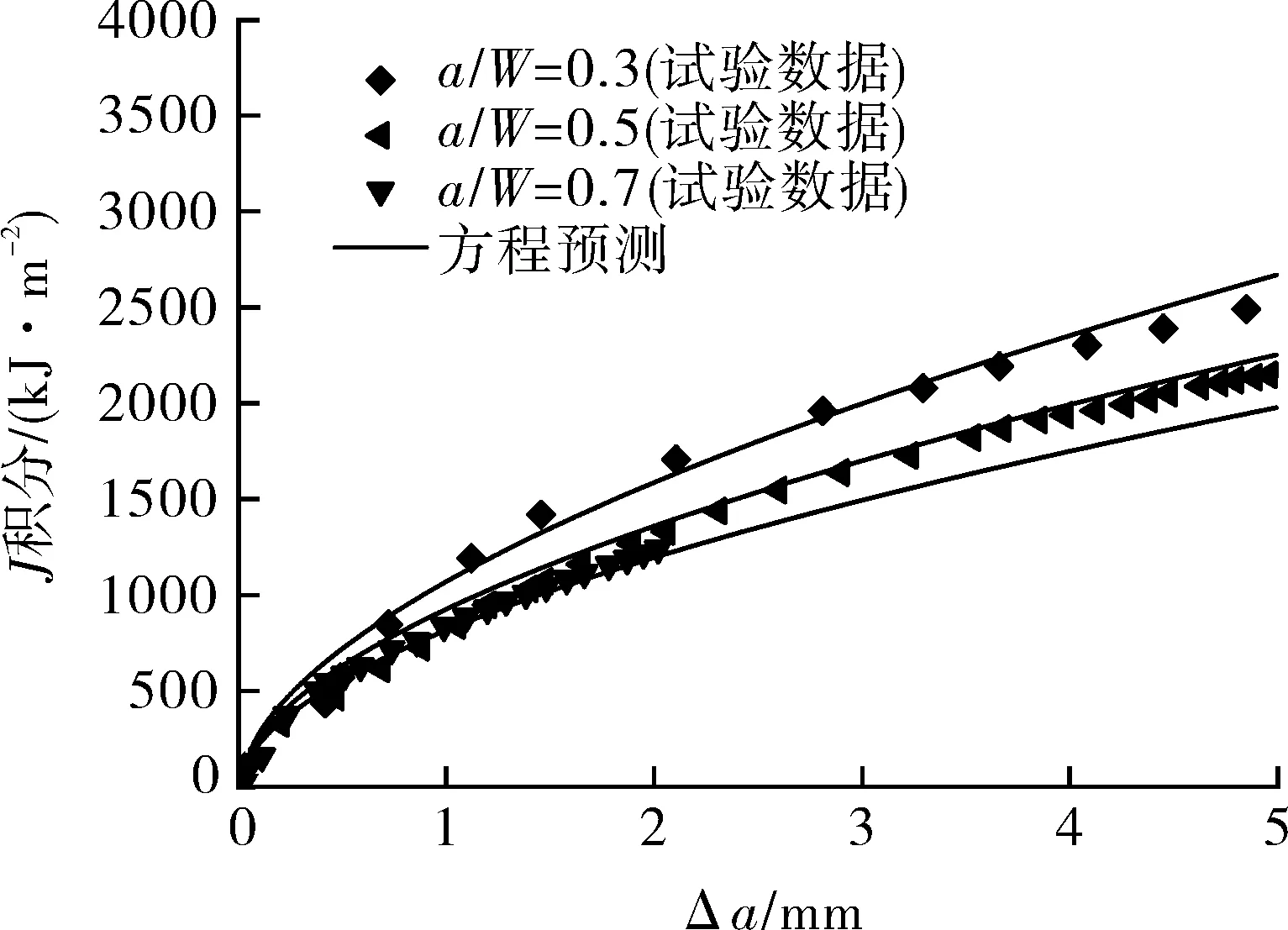
((b)与试验曲线的对比

图8 7个试样建立的方程预测的J-R阻力曲线与数值模拟曲线和试验曲线的对比

上述式(13)是用7个不同a/W的试样建立的，为减少试验和数值计算成本，希望用少量不同拘束的试样建立材料拘束相关的J-R阻力曲线方程。为探明少量试样建立方程的可行性及精度，选取a/W=0.1,0.25,0.4，0.7的4个试样建立方程。通过采用与上述相同的方法，计算得到拘束相关的J-R阻力曲线方程如下：

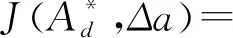
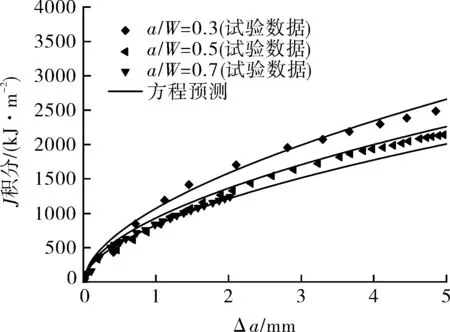
(14)

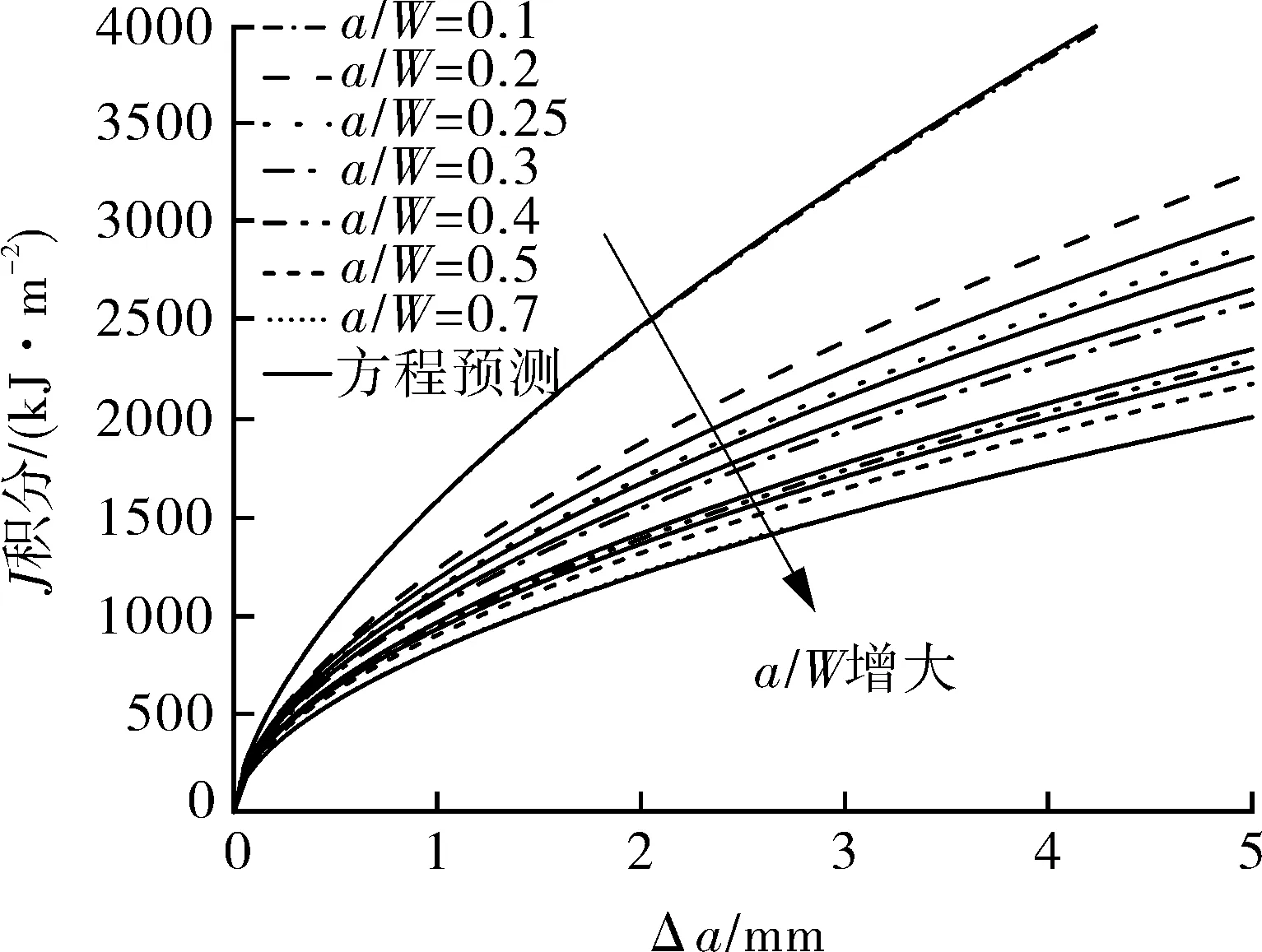
用式(14)计算预测的不同a/W试样的J-R阻力曲线与数值模拟曲线[20]和试验曲线[20]的对比如图9所示，发现二者吻合良好，表明采用少量不同拘束的试样也可以建立材料拘束相关的J-R阻力曲线方程。

(a)与数值模拟曲线的对比

(b)与试验曲线的对比

图9 4个试样(a/W=0.1,0.25,0.4，0.7)建立的方程预测的J-R阻力曲线与数值模拟曲线和试验曲线的对比

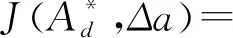
(15)

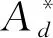
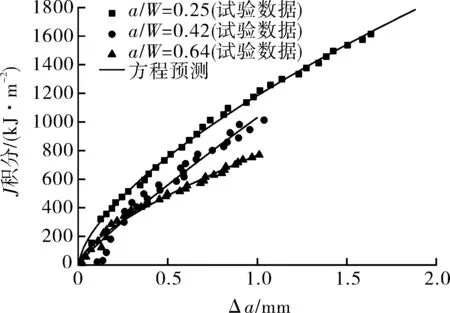
图10 方程预测的X80钢SEN(B)试样的J-R阻力曲线与试验曲线的对比

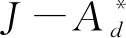
4 结语