一种考虑加速度需求的车速自适应控制方法

熊璐,付志强,柏满飞,章仁燮

(1.同济大学汽车学院,201804,上海;2.同济大学中德学院,201804,上海)

智能车运动控制包含横向控制和纵向控制,其中纵向控制是通过控制油门和制动来达到上层系统规划出的期望车速和期望加速度[1]。由于车辆模型参数具有不确定性及非线性的特点,提高车辆纵向控制方法的鲁棒性具有重要研究价值。

纵向控制方法主要有比例积分微分(proportion integral derivative,PID)控制、基于车辆模型的闭环反馈控制和自适应控制等方法。赵盼提出了利用专家规则的PID车速控制方法,建立了油门和刹车的协调切换逻辑,根据专家规则来调整PID参数[2]。Zhou提出了一种增量式PD模糊逻辑控制器,利用车速跟踪误差和误差的变化率作为输入进行调节,有效地降低了车速稳态误差[3]。陈刚等提出了一种模糊自适应PID控制方法,利用模糊控制方法实现参数自适应整定[4]。但是针对车辆纵向控制的非线性特点,这些PID控制方法需要调节很多参数,并且忽略了外界环境不确定性可能会引起系统的不稳定。还有一部分方法是利用车辆动力学模型进行反向求解来控制输入。Shakouri等使用了线性化的车辆模型来设计增益调度的线性二次方程,将其分别作用于油门和制动[5]。Attia等提出了基于动力传动系统动力学模型的车速控制方法,分别控制油门和制动输入,并分析了系统的稳定性,但是没有考虑加速度需求[6]。Zhu等提出了基于模糊控制的加速度控制方法,基于建立的车辆模型分别设计了油门和制动模糊控制器,仿真结果表明控制效果优于传统PID控制[7]。为了考虑车辆参数的不确定性和外部干扰,文献[8-9]提出了基于时变参数的自适应加速度控制器,通过改进后线性化的车辆模型设计自适应控制律,该方法不需要复杂的车辆模型及参数,即可达到很好的跟踪效果。

综上所述,大部分文献都忽略了道路阻力变化对纵向控制的影响,而且都是单一的车速控制或者加速度控制,没有同时考虑到车速控制过程中的加速度需求。因此,本文考虑了道路阻力的变化,针对时变参数采用自适应遗忘因子递归最小二乘法(forgetting-factor recursive least square method,FFRLS)对道路阻力进行估计,并且基于条件积分方法分别设计车速控制律和加速度律,通过一阶系统积分的自动调节保证了车速控制和加速度控制的协调切换,使得纵向控制在大误差下几乎没有超调。通过仿真和实车试验验证了本文自适应控制方法的有效性,并且验证了在坡度路面上,本文方法的跟踪效果优于未加入道路阻力估计器的跟踪效果。

1 车辆纵向动力学模型

根据车辆纵向运动过程中的受力状态,在不考虑纵向和侧向耦合的情况下,忽略转向在纵向的分力,假设车辆行驶在坡度角为α的道路上,车辆纵向受力可以简化为如图1所示的单轮模型。

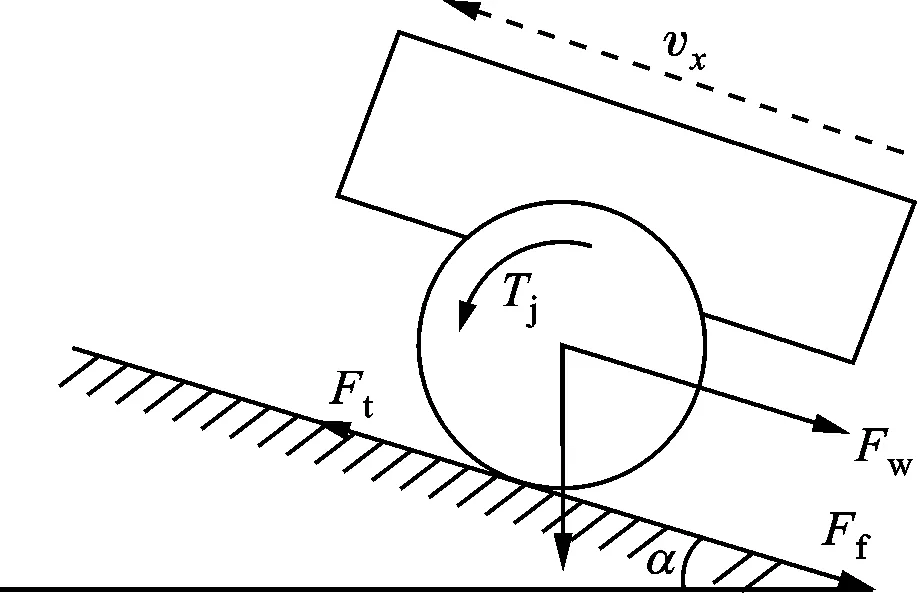
Ft:行驶驱动力;Fw:空气阻力;Ff:滚动阻力;vx:纵向车速;Tj:驱动轮力矩图1 单轮车辆模型

车辆的整体纵向运动方程为

Ft=Fw+Fψ+Fj

(1)

式中:Fj为加速阻力;Fψ为道路阻力,Fψ=Ff+Fi,Fi为坡度阻力。

对于前驱车辆,将纵向受力代入式(1)可得

(2)

2 考虑加速度的车速自适应控制方法

基于车辆纵向动力学模型,采用FFRLS对道路阻力进行估计,将纵向动力学模型中的非线性项通过前馈进行抵消,并分别建立基于条件积分方法的车速和加速度控制律,设计过渡控制律将其耦合,建立切换策略保证车速能够快速跟踪并且在此过程中不会出现超调。

2.1 道路阻力估计

汽车行驶过程中,驱动力用来克服空气阻力、加速阻力、道路阻力,其中空气阻力可以通过查阅相关参数计算得到,加速阻力可以利用惯导得到的加速度计算得到,但是道路阻力与道路条件有关,无法直接获得。道路阻力包括滚动阻力和坡度阻力,占行驶阻力的一大部分,是影响车辆纵向动力控制的重要参数,因此需要设计估计器进行估计。

对于渐变参数的估计,传统的FFRLS采用定值遗忘因子能使估计值较快地收敛,但是对于突变的参数的估计,传统的FFRLS由于遗忘因子取为大于0.9的定值,历史数据的权重很大,导致估计值不能快速地收敛。因此,本文采用自适应FFRLS,通过定义遗忘因子的自适应法则来优化估计方法的性能[10]。

(3)

式中:L(k)为递推增益;P(k)为协方差;λ为遗忘因子,取值区间为(0,1]。遗忘因子的大小关系着辨识精度和收敛速度,取值必须综合考虑。

设遗忘因子的初值为λ0,根据观测向量纵向力的预测误差来确定遗忘因子的取值。观测向量纵向力的预测误差和预测误差的方差分别为

(4)

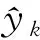
当预测误差的方差超过事先设定的阈值时,需要立刻减少遗忘因子至λ′,之后随着样本数据的增加再慢慢增大遗忘因子,降低估计值对噪声的敏感性。实际的遗忘因子计算公式为

(5)

2.2 车速跟踪控制方法

车速控制律基于条件积分方法,能够防止由于执行器约束而长时间无法镇定系统、因而导致积分运算发散从而使控制方法失效的现象[11],并且能够保证设计的运动学控制器控制律有界。不考虑轮胎出现滑移,对于前轮驱动的车辆,设控制律为uT∈[-Tmax,Tmax],式中:uT为前轮驱动力矩;Tmax为最大驱动力矩取值,需要综合考虑电机的驱动性能和地面附着系数。Tmax的计算公式为

(6)

式中:Pn为电机额定功率;it为电机到车轮的传动比;nn为电机额定转速;μ为路面附着系数;Fz为前轴垂向载荷。

不考虑轮胎滑移,将式(1)和(2)转换为

(7)

将式(7)转换为镇定系统,车速跟踪误差ev=vd-vr,式中vr是实际车速,vd是期望车速。令uT=TF,通过驱动力矩转换得到

(8)

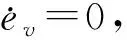
(9)

式中:Tf为前馈计算中间转化量;Tfore为前馈控制率;sgn为符号函数。

(10)

式中:k0和θ0为车速控制器参数,均大于0;σ为积分中间变量;sat为饱和函数。

当积分运算未饱和时,即|s1|<1时,将式(10)代入闭环系统中可得

(11)

建立李雅普诺夫函数V如下

(12)

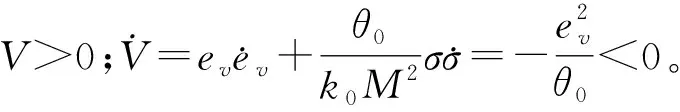
当|s1|≥1时,积分运算中间变量σ收敛于ΔT,控制律收敛于最大值,此时积分运算的导数为

(13)

2.3 耦合的车速和加速度控制方法

为了在跟踪期望车速的过程中满足上层系统的期望加速度需求,本文将加速度控制模式由加减速度跟踪控制模式和加减速度过渡控制模式组成,将车速控制律和加速度控制律耦合,基于条件积分算法设计了加速度控制律,通过积分自动调节和建立切换策略,保证了车速控制模式和加速度控制模式的平滑切换。

2.3.1 车速控制模式和加速度控制模式的切换策略 本文提出的自适应控制方法一共有3种控制模式——车速控制模式、加速度跟踪控制模式、加速度过渡控制模式,其中加速度过渡控制模式是为了使加速度跟踪控制模式能平顺地切换到车速控制模式。本文方法需要制定车速控制模式和加速度控制模式之间切换的策略,并确定车速控制区间、加速度跟踪控制区间、加速度过渡区间,以及各个区间之间切换的条件,切换策略示意如图2所示。

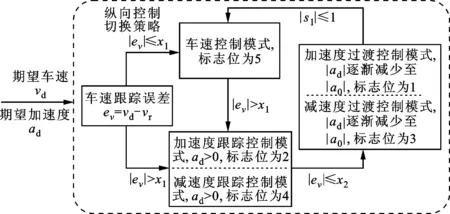
图2 切换策略示意图

首先需要设置车速控制阈值x1,当车速跟踪误差|ev|>x1时,进入到加速度跟踪控制模式,该模式具体分为加速度跟踪控制模式和减速度跟踪控制模式,分别对应标志位2和4;设置车速控制阈值x2,如果车速跟踪误差的绝对值减少到设定的阈值|ev|≤x2(x2≤x1),则切换到加速度过渡控制模式,具体分为加速度过渡控制模式和减速度过渡控制模式,分别对应标志位1和3;设置加速度控制阈值a0,之后如果实际车速跟踪上期望车速,通过积分自动调节,期望加速度绝对值逐渐收敛到较小值a0,有效避免了切换过程中出现的抖动,平滑切换到车速控制模式,即|ad|≤|a0|,对应标志位为5。若开始车速误差|ev|≤x1,则进入车速控制模式,之后如果期望车速变化太快导致车速误差大于阈值x1,则切换到加速度跟踪控制模式。

2.3.2 加速度控制算法设计 基于车辆纵向动力学方程,利用条件积分算法设计加速度控制律。与车速控制律类似,定义加速度跟踪误差ea=ad-ar,式中ar表示实际加速度,引入积分运算,满足执行器约束,则加速度控制律为

(14)

式中:θa和ka为控制器设计参数,均大于0。

根据条件积分算法的饱和特性,在车速控制律饱和时,用加速度控制律代替车速控制饱和时的控制律,将两者耦合在一起,即当车速跟踪误差|ev|>x1时,令积分系数k0取较大的值使其快速饱和,达到跟踪期望加速度的目的,此时有

(15)

2.3.3 过渡控制律设计 传统的车速控制器和加速度控制器都是两个不同且相互独立的控制器,当从加速度控制模式切换到速度控制模式时,车速不可避免地会出现抖动甚至是严重超调,进而影响系统的稳定性。本文利用一阶系统积分的收敛特性来设计过渡控制律。由于一阶系统的特性,在加速度控制模式时,积分运算中间变量σ逐渐收敛于ΔT。当车速误差绝对值小于设定的阈值x2时,控制模式从加速度控制模式进入到过渡控制模式,在过渡过程中期望加速度为a0,此时加速度控制律为ua0,利用这一特性,将过渡控制律设计为

(16)

此时,控制律逐渐收敛于ua0,加速度也逐渐减小至a0。积分系数k0决定了收敛速度,若收敛速度太快,则不能保证快速地跟踪车速,若收敛太慢,则会降低车速跟踪的平顺性。因此,k0的取值需要满足当σ收敛到ua0时,控制模式刚好进入到车速控制模式。假设加速度在过渡控制模式中是均匀减小的,车速误差阈值x2与加速度及收敛时间t0的关系为

(17)

为了获得积分系数k0与收敛时间t0的关系,仿真了不同σ收敛到ua0的时间,结果见表1。

表1 积分系数与收敛时间的关系

通过拟合表格中的数据及结合式(17)可得

(18)

2.3.4 控制算法稳定性分析 耦合的控制算法在车速控制阶段的稳定性已经证明,过渡控制过程中一阶系统的控制律逐渐收敛,在加速度控制阶段,当积分未饱和时,代入到闭环系统中可得

(19)

建立李雅普诺夫函数如下

(20)

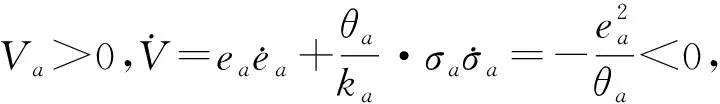
3 仿真试验

为了验证道路阻力估计器的准确性以及本文方法的跟踪效果,在Carsim软件中搭建相同的车辆模型,车辆参数如表2所示。通过Simulink/Carsim联合仿真来验证控制策略的有效性,根据仿真效果来调整不同模式下耦合的控制器参数,结果如表3所示。

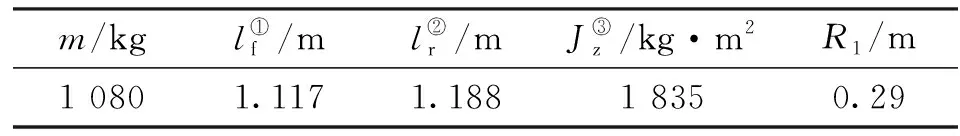
表2 车辆参数

①:质心到前轴的距离;②:质心到后轴的距离;③:车辆横摆转动惯量。

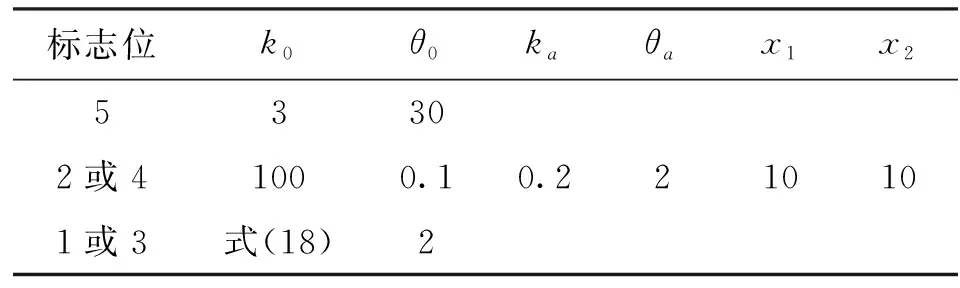
表3 控制器参数

3.1 道路阻力估计器仿真试验

在纵向控制中,为了验证道路阻力估计器的估计效果,对比了实际的道路阻力和估计的道路阻力之间的误差。估计的道路阻力如图3所示,仿真工况如下:车速为30 km/h;路面为水平路面和6°坡度路面;附着系数均为0.85。

车辆在水平路面行驶时,只有滚动阻力和未知阻力。从图3中可以看出,估计的道路阻力在不到1 s内就收敛到了稳定值285 N。计算的滚动阻力为188 N,因此未知阻力为97 N。在坡度路面,车辆受到了较大的坡道阻力。图3中估计的道路阻力为1 465 N。计算的道路阻力为1 434 N,未知阻力取水平路面的97 N,因此实际的道路阻力为1 631 N。估计的道路阻力与实际的道路阻力误差为4.1%,在可接受的范围内,该估计器的效果得到了验证。

3.2 本文方法仿真试验

为了验证本文方法在水平路面和坡度路面的控制效果,设置以下2种试验工况。

工况一:水平路面,路面附着系数为0.85。第1组试验是期望车速从0逐渐加速到50 km/h,再逐渐回到0,车速控制仿真效果如图4所示;第2组试验是为了验证在车速跟踪误差较大时的跟踪效果,期望车速从0阶跃加速到50 km/h,期望加速度为2 m/s2,再减速到20 km/h,期望减速度为-3 m/s2,车速控制仿真效果如图5所示,对应的加速度控制仿真效果如图6所示。

从图4和图5中可以看出:本文方法在车速跟踪误差较小和车速跟踪误差较大的情况下,都几乎没有超调现象,稳态误差小于0.2 km/h。从图6中可以看出:在车速跟踪误差大于设置的阈值时,纵向控制的阶跃响应性能较好能,能够满足期望加速度的需求。

图4 纵向车速控制阶跃响应

图5 考虑加速度的纵向控制阶跃响应

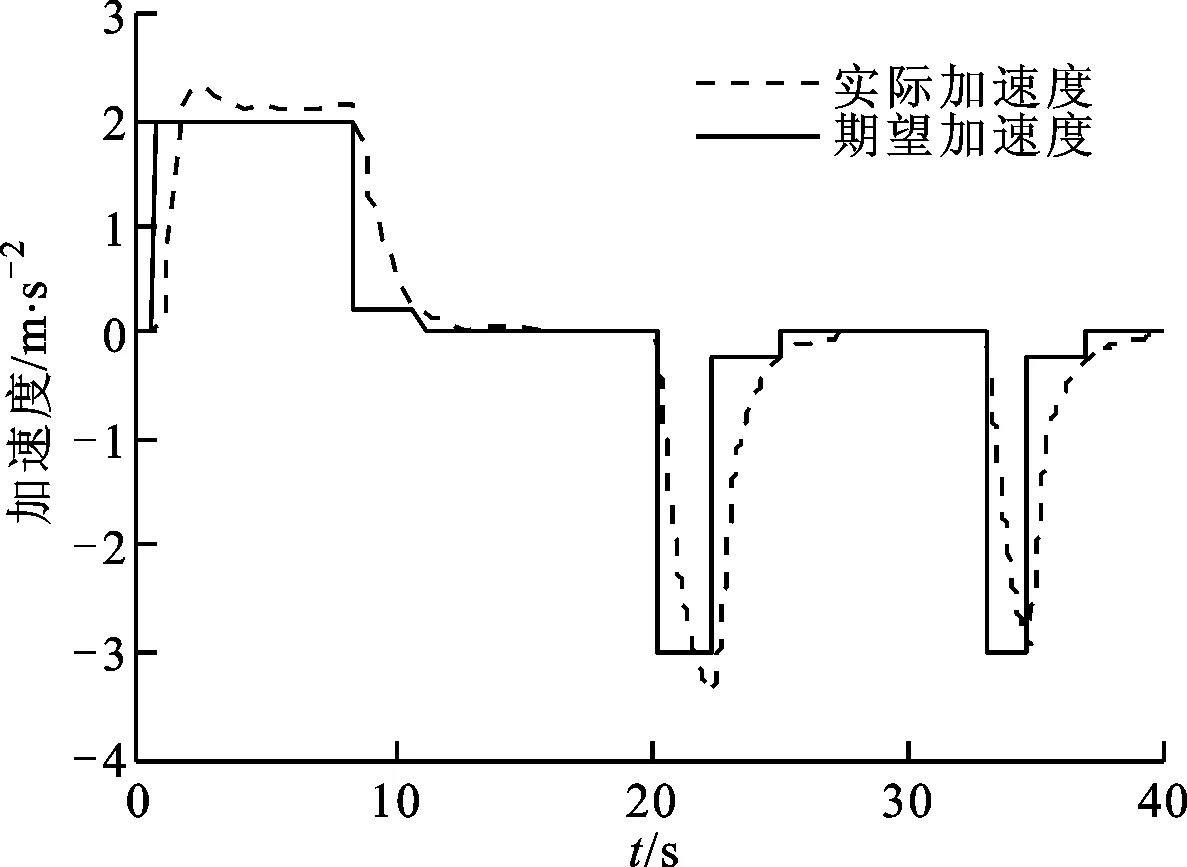
图6 加速度跟踪效果

工况二:8°坡度路面,路面附着系数为0.85。试验是期望车速从0到10 km/h,目的是为验证纵向控制方法在坡度路面上的跟踪效果。在坡度路面上的车速控制效果如图7所示。

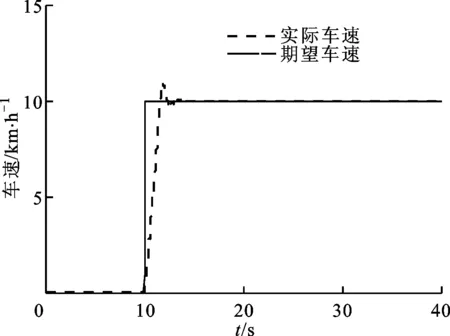
图7 坡度路面上纵向控制跟踪效果

从图7可以看出,在坡度路面上,实际车速迅速达到期望车速,稳态误差小于0.2 km/h,但相对超调量为0.5%。本文算法在坡度路面上的跟踪效果得到了验证。

综合上述2种工况下的跟踪效果可知,本文提出的考虑加速度需求的自适应车速控制方法在水平路面和坡度路面都能有较好的跟踪效果。

4 实车试验

在仿真试验的基础之上,进行实车试验来验证本文方法的跟踪效果,试验平台如图8所示,该平台经过改造后驱动电机可以实现线控。纵向车速由车辆底盘轮速信号转换得到,加速度通过惯导设备RT3003获取,嵌入式控制器用于数据采集和实时控制,如图9所示。试验场地为图10中的圆形试车场,该试车场包括坡度路面。

图8 试验平台 图9 试验车内部图

图10 试验场地

为了验证本文方法对期望车速的跟踪能力,在水平路面设计阶跃响应试验工况,在坡道上设计上坡起步和下坡车速跟踪试验工况,分别与未加入道路阻力估计器的方法进行对比分析。

图11是本文方法在水平路面0～50 km/h的阶跃期望车速的跟踪效果,可以看出:在跟踪稳态车速时,误差不到0.2 km/h,与图4中的仿真效果几乎相同,能够快速准确地响应到期望车速;当期望车速从30 km/h增加到50 km/h时,实车试验的车速有些超调和抖动,但相对超调量低于0.5%,在可以接受的范围之内。由此,纵向控制器的稳态跟踪能力得到了验证。此外,由于水平路面上道路阻力相对较小,未加道路阻力估计器的跟踪效果和自适应控制跟踪效果差别不大。

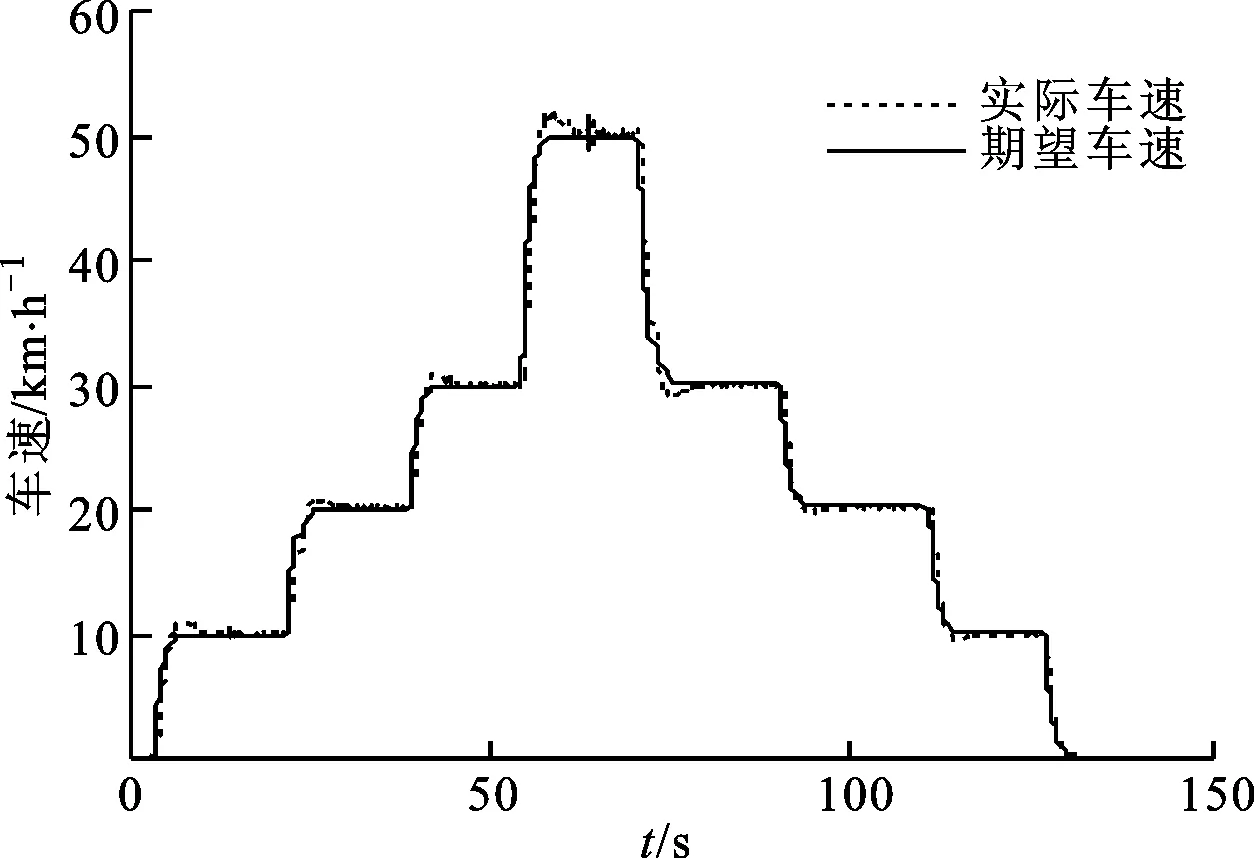
图11 本文方法的阶跃响应

在坡度路面上坡的车速跟踪效果如图12所示,下坡跟踪效果如图13所示,可以看出:未加估计道路阻力的方法在坡道上起步时有超过2 s的溜坡现象,且无论上坡还是下坡,车速均有明显的超调;本文方法在坡道上起步时只有不到1 s的溜坡现象,且车速无明显超调,基本上可以忽略坡度对车速控制的影响,和图7的仿真效果基本相同。由于实车试验时对阶跃的期望车速加了滤波,所以实车试验的车速几乎没有超调,跟踪效果更好,而仿真中出现不超过1%的相对超调量,可以接受。显然,本文方法控制效果更好,能在一定程度上抑制路面坡度对车速控制的影响。

图12 上坡车速跟踪效果对比

图13 下坡车速跟踪效果对比

为了验证本文方法在跟踪期望车速过程中跟踪期望加速度的能力,在水平路面上设计了不同的期望加速度跟踪试验。

加速度控制试验一:水平路面,路面附着系数0.8,50 km/h的阶跃期望车速响应,加速度为1 m/s2,减速度为-1 m/s2。将本文方法与传统的PI控制方法进行对比。由于传统的PI控制方法无法同时跟踪期望车速和期望加速度,因此分别进行车速跟踪和加速度跟踪试验。

图14和图15是期望加速度较小时,控制方法的试验效果对比,可以看出:本文方法相比传统的PI控制方法能够在较大车速误差下超调较小,并且能够在跟踪加速度时满足车速的需求。本文方法在一开始就进入到加速度跟踪控制模式中,实际加速度能快速稳定地跟踪上期望的加速度,稳态误差在±0.1 m/s2;在过渡控制模式中,实际加速度的绝对值逐渐从初始值减小至0.2 m/s2,实际车速平稳地跟踪上期望车速且毫无超调。传统的PI控制方法超调相对较大,整体响应较慢,无法在跟踪加速度时满足车速的需求。在大车速跟踪误差下,本文方法的跟踪效果得到了验证。

图14 纵向车速控制跟踪效果对比及相应的标志位

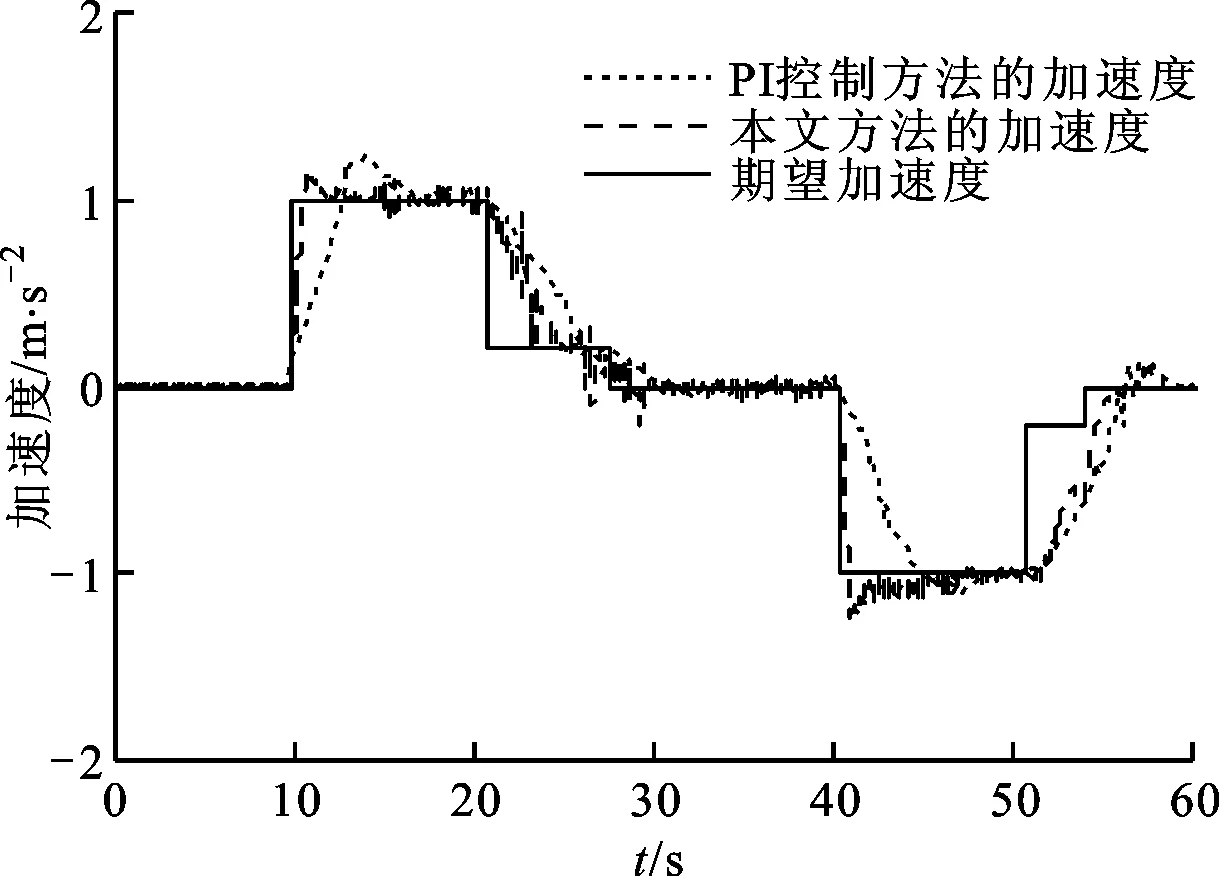
图15 纵向加速度控制跟踪效果对比

加速度控制试验二:水平路面,路面附着系数0.85,期望车速从0到50 km/h再到20 km/h再到0的阶跃期望车速响应,加速度为2 m/s2,减速度为-3 m/s2。

图16和图17是期望加速度较大时,控制算法的实车试验效果对比。与仿真试验效果图5和图6相比,二者基本相同,但实车试验减速控制中出现的超调较大。加速度跟踪过程中,仿真效果比实车试验效果好,仿真效果的稳态误差为±0.15 m/s2,实车试验的稳态误差为±0.1 m/s2。同时可以看出:传统的PI控制方法在车速跟踪时无法同时满足期望加速度的需求,在减速过程中,本文方法响应较快,并且超调较小;当期望车速为50 km/h时,阶跃变化后,本文方法的实际加速度能快速准确地跟踪期望加速度2 m/s2,稳态误差不超过0.1 m/s2,同时在加速度过渡模式逐渐收敛到0.2 m/s2,使加速度跟踪控制模式能够平滑地过渡到车速控制模式;当期望车速从50 km/h突然降到20 km/h时,本文方法的实际减速度也能快速准确地跟踪期望减速度-3 m/s2,误差不超过0.1 m/s2,同时在加速度过渡模式快速收敛到-0.2 m/s2,能够在较大的速度时紧急制动到给定车速,对于紧急避障有重大意义,而传统的PI控制方法在减速度跟踪过程中响应较慢,无法用相同的参数来满足各种工况,并且无法证明闭环系统的稳定性。综上,本文提出的考虑加速度需求的车速控制算法能够满足智能车运动控制的需求,并且跟踪效果较好。

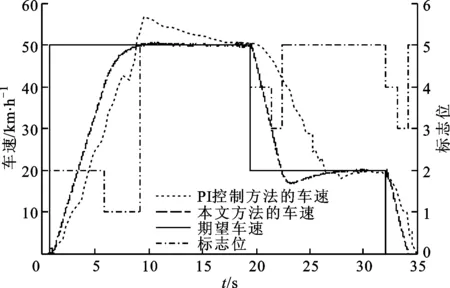
图16 纵向车速控制跟踪效果及相应的标志位

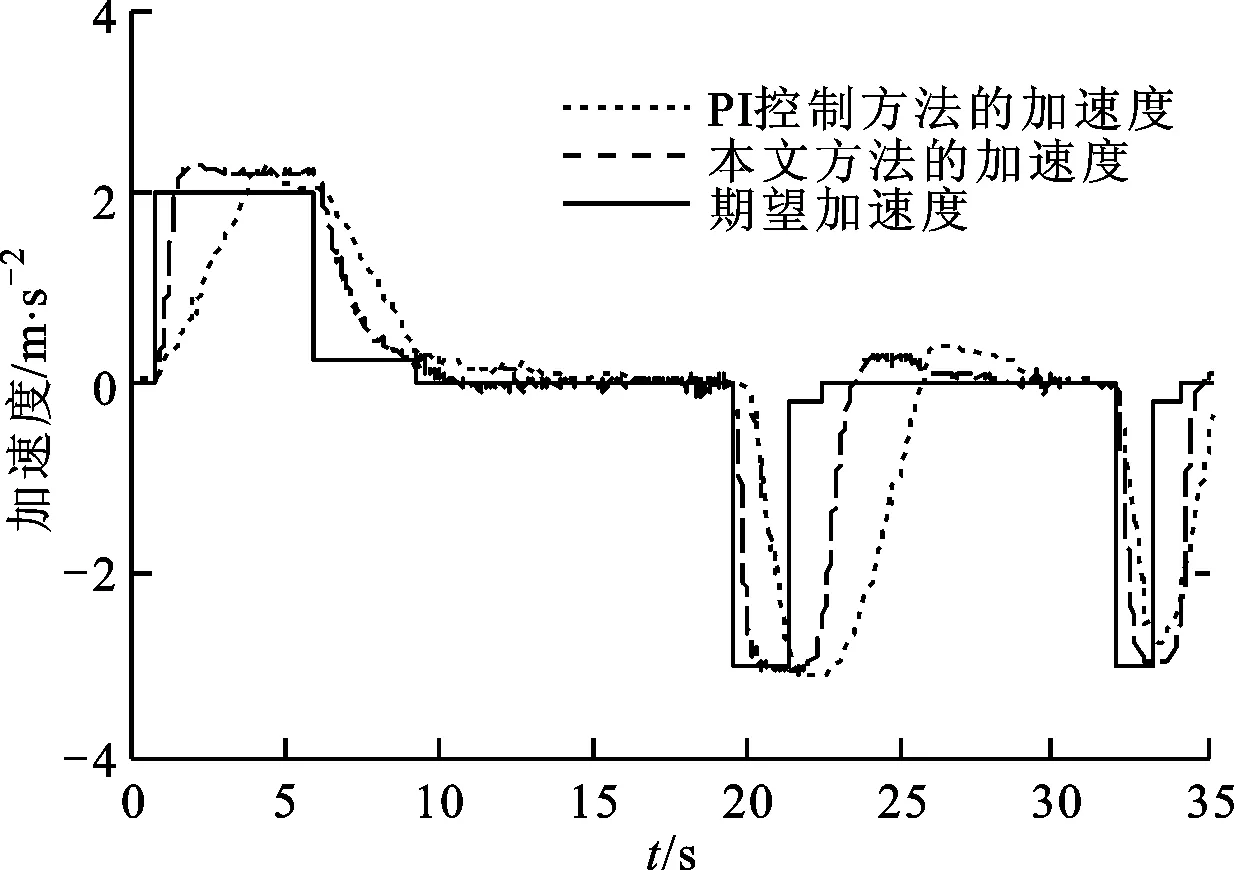
图17 纵向加速度控制跟踪效果对比

5 结 论

本文提出了一种考虑上层加速度需求的车速自适应控制方法。首先,针对智能车行驶中道路阻力的不确定性,基于FFRLS算法设计了道路阻力估计器,通过仿真及实车试验,验证了车速自适应控制方法在坡道上的跟踪效果优于未加入估计器时的效果。之后,考虑上层的期望加速度需求,基于条件积分算法设计了耦合的车速和加速度控制律,通过积分自动调节和切换策略,保证了同时跟踪期望车速和期望加速度,通过仿真及实车试验验证了本文方法的有效性。