钻孔工件移动热边界条件估计及温度场重构

吕财,王广军,2,陈红,2,章广祥,陈泽弘

(1.重庆大学动力工程学院,400044,重庆;2.重庆大学低品位能源利用技术及系统教育部重点实验室,400044,重庆)

孔钻削是机械加工过程常见的金属去除成型工艺[1-2],与其他切削工艺相比,钻削是半封闭状态加工,摩擦严重、散热困难。在钻孔过程中,工件的温度分布是一个重要的参数,它不仅会影响钻具的寿命,还直接影响到工件的性能指标,如残余应力、尺寸误差和加工表面的硬度等。因此,全面了解孔钻削过程中工件的温度分布,有助于提高加工效率和产品工件的加工质量[3-5]。

通常,实验测量只能获得部分的温度信息,为了获得钻孔工件完整的瞬态温度场,必须明确进入工件的瞬时热负荷。由于进入工件的瞬时热负荷难以直接准确测量,借助导热反问题方法,利用工件内部或表面的部分温度测量信息反求进入工件的瞬时热负荷,进而重构工件的瞬态温度场,是一种方便有效的解决方案。

目前,求解导热反问题的方法主要有梯度类优化方法[6-7]、正则化技术[8]、分散式模糊推理[9-10]、顺序函数法(SFSM)[11-12]、随机优化方法[13-14]等。其中,SFSM利用未来一段时间内的测量温度信息反演当前时刻的未知参数,在非稳态导热反问题中得到了广泛的应用。然而,它需要假定未来一段时间内未知变量的变化形式,这会影响反演结果的准确性[15]。针对这一问题,Wang等结合系统预测控制思想,建立了一种基于动态矩阵控制(DMC)的反演方法,实现了非稳态导热系统多个热边界条件的同时反演[16-17]。与SFSM相比,DMC反演方案无需假定待反演参数在未来时间段的变化形式,降低了反演结果对于未来观测信息的依赖性,提高了反演结果的可靠性。作为一种顺序反演方案,DMC为钻孔工件的温度场在线重构提供了可能。

关于导热反问题方法在钻孔传热过程中的应用研究已经积累了一些成果。Huang等采用最速下降法反求了进入钻头的热流量[18]。Tai等基于序列二次优化方法研究了深孔钻削时钻孔壁面和底面产生的热量,发现深孔钻削时预测工件温度需要考虑孔壁面热量的影响[19]。De Sousa等建立了一种基于格林函数和动态观测器的反演方法,并将其用于估算钻孔过程中进入工件的瞬时热流量[20]。需要说明的是,在工件的钻孔加工过程中,随着钻具的持续运动,工件的受热边界不断发生移动,系统输入(瞬态热负荷)与系统输出(测点处温度)之间的动力学映射关系可能发生明显变化。本质上,钻孔传热系统是一类非线性传热系统,相对于线性系统,非线性传热系统反问题的不适定性更加突出[7]。

本文基于模型预测控制思想研究了钻孔工件移动边界热流反演及温度场重构问题,以钻孔工件传热模型为基础,建立了工件瞬态温度场阶跃响应函数模型以及工件温度预测模型;利用工件的部分温度测量信息,通过滚动优化实现工件移动传热边界条件的反演及工件瞬态温度场的在线重构。文中利用数值仿真试验验证了上述方法的有效性,并详细讨论了钻具进给速度、温度测量误差、测点数等对反演结果的影响。

1 钻孔工件温度分布数学模型

钻孔工件的简化物理模型如图1所示。工件在加工过程中,一方面受到来自钻削产生的部分摩擦热q(t),另一方面与环境进行对流换热。对工件的传热过程引入如下假设[5,18,20]:

①由于工件的对称性,只考虑工件沿径向和轴向的传热,将其简化为二维传热问题;

②工件的对称面视为绝热,其他边界则与环境发生对流换热;

③进入工件的热负荷沿孔径方向均匀分布,只随时间发生变化;

④工件材料的热物性各向同性且恒定。

根据上述假设,建立圆柱坐标下钻孔工件温度分布数学模型

图1 钻孔工件的简化物理模型

(1)

T(r,z,0)=T0(r,z)

(2)

(3)

(4)

(5)

式中:λ、ρ和c分别为工件的导热系数、密度和比热容;T0(r,z)为工件的初始温度;q(t)为进入到工件的瞬时热流密度;T∞(t)为环境温度;h为对流换热系数;n为界面的法线方向。

2 模型预测控制方法求解反问题

2.1 反问题目标函数

如果方程组(1)～(5)中的其他条件均已知,移动边界热流q(t)未知时,根据温度测点m(m=1,2,…,M)在时刻k,k+1,…,k+R-1的测量值来估计qk,构成了对应的导热反问题。这里的R为预定的未来时间步数,qk为q(t)在k时刻的估计值。

上述的导热反问题可以通过使以下目标函数最小化求解

minJ(Q)=(Y-T)T(Y-T)+αQTQ

(6)

2.2 预测模型

(7)

(8)

将上述方程转化为矩阵方程

(9)

定义工件传热模型的阶跃响应函数

X(r,z,t)=∂T(r,z,t)/∂qk

(10)

X(r,z,t)反映了qk对温度场T(r,z,t)的影响程度。将方程组(1)～(5)对qk求导,则在[tk,tk+R-1]时间段内X(r,z,t)应满足下列的阶跃响应方程组

(11)

X(r,z,tk-1)=0

(12)

(13)

(14)

(15)

由方程组(11)～(15)可以看出,X(r,z,t)随着边界AB的移动而发生变化。因此,可以根据有限容积法和高斯赛德尔迭代法在每一时刻求解上述的阶跃响应方程组,得到阶跃响应函数的离散值,进而按下式来确定测点m处的阶跃响应系数

(16)

2.3 滚动优化

模型预测反演方法通过采用滚动优化获得边界热流向量Q=[qk,qk+1,…,qk+R-1]T。

将式(6)对Q求导,并令dJ(Q)/dQ=0,得到移动边界热流向量的最优估计值

(17)

式中E为R阶的单位矩阵。

在当前时刻k,只需根据式(17)确定即时热流量qk,下一时刻按同样的优化方法求得qk+1,此即滚动优化策略。

由式(17)得即时热流量的最优估计值为

(18)

d=[1,0,…,0]1×R

3 仿真试验结果及讨论

3.1 仿真试验条件

对于图1所示的钻孔工件传热系统,其结构和物理参数为:外半径r2=2 cm,内半径r1=0.5 cm,高度H=5 cm;工件的材料为AISI 1018碳钢,导热系数λ=51.9 W·m-1·K-1,密度ρ=7 870 kg·m-3,比热容c=486 J·kg-1·K-1。

取工件初始温度T0(r,z)=20 ℃,对流换热系数h=30 W·m-2·K-1,环境温度T∞(t)=20 ℃。

按式(19)和式(20)给定两组不同变化形式的热流密度

q1(t)=6+20sin(πt/24)e-0.2t(MW·m-2)

(19)

(20)

根据网格无关性验证结果,在区域离散时,取空间步长Δr=Δz=0.5 mm,时间步长Δt=0.5 s。

仿真试验过程中,假定温度测点均匀布置于工件的外表面,具体位置见表1。

表1 温度测点位置

考虑到实际温度测量结果不可避免地存在测量误差,在数值仿真试验中,按下式模拟测点处的实际测量温度

(21)

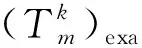
为了评估反演方案的准确性,引入均方根误差Sq及平均相对误差η

(22)

(23)

式中:K为待反演热流总的时间离散点数;(qk)exa为热流密度q(t)在k时刻的真实值。

3.2 移动热边界条件反演

取未来时间步数R=3,钻具进给速度v=0.002 m/s,测量误差的标准差σ=0,利用测点T2和T4提供的温度信息反演未知热边界条件q(t)。图2和图3分别给出了边界热流q1(t)和q2(t)的反演结果。

图2 热流q1(t)的反演结果

图3 热流q2(t)的反演结果

由图2和图3可知,对于不同变化形式的移动边界热流q(t),本文方法均可以获得良好的反演结果,证明了本文反演方案的有效性。

3.3 进给速度的影响

采用测点T2和T4的温度信息,在R=3、σ=0的条件下,分别取v=0.001,0.002,0.003 m/s来考察钻具进给速度对反演结果的影响,如图4和图5所示,对应的反演误差见表2。

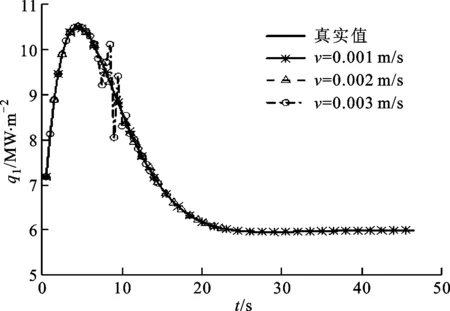
图4 不同进给速度下q1(t)的反演结果

图5 不同进给速度下q2(t)的反演结果

v/m·s-1η/%q1q2Sq/W·m-2q1q20.0010.010.021.04×1031.77×1030.0020.380.503.14×1044.08×1040.0033.236.232.92×1055.35×105

由图4、图5及表2可知,随着钻具进给速度的增大,导致传热过程非线性特征进一步加强,当R一定时,对应的热边界条件反演精度有所降低,但在仿真试验所讨论的进给速度范围内,仍然可以获得较好的反演结果。

3.4 测量误差的影响

采用测点T2和T4的温度信息,在R=3、v=0.002 m/s的条件下,分别取σ=0.01,0.03,0.05来考察温度测量误差对反演结果的影响,如图6和图7所示,对应的反演误差见表3。

图6 不同测量误差下q1(t)的反演结果

图7 不同测量误差下q2(t)的反演结果

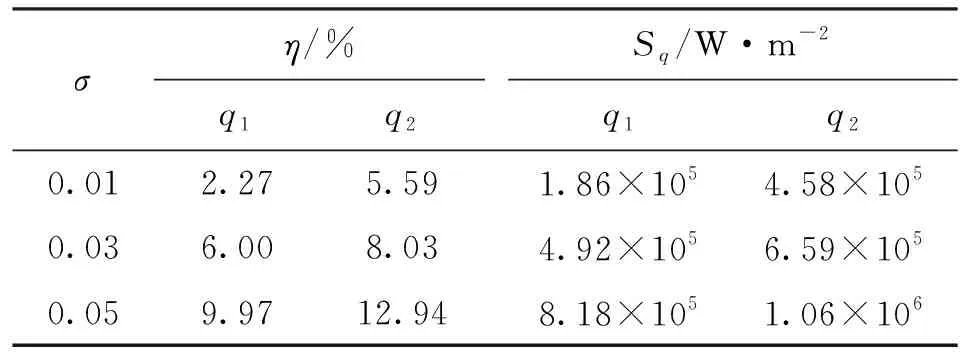
ση/%q1q2Sq/W·m-2q1q20.012.275.591.86×1054.58×1050.036.008.034.92×1056.59×1050.059.9712.948.18×1051.06×106

根据σ=0.05条件下的反演结果q1(t)和工件的传热模型,重构工件的瞬态温度场如图8所示。作为对比,图9给出了空间点1(0.5 cm,4.5 cm)、2(0.5 cm,3.5 cm)、3(0.5 cm,2.5 cm)、4(0.5 cm,1.5 cm)和5(0.5 cm,0.5 cm)处工件温度的重构值和根据实际热边界条件得到的模拟结果。

(a)t=2 s(b)t=7 s(c)t=12 s(d)t=17 s(e)t=22 s 图8 工件瞬态温度场的重构结果

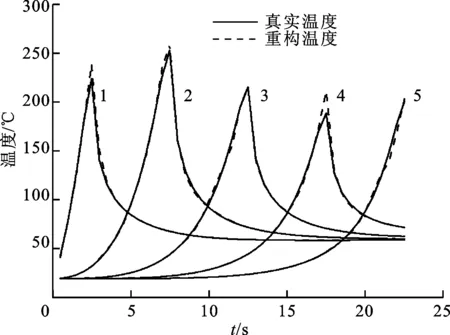
图9 σ=0.05时工件内部温度重构结果

由以上结果可知,虽然随着温度测量误差的增大,移动边界热流的反演精度有所降低,但仍然可以获得较好的反演结果,表明本文的模型预测反演方案具有一定的抗干扰能力。

3.5 测点数的影响

在R=3、σ=0.01、v=0.002 m/s的条件下,分别取测点数M=1,2,5进行数值试验,考察测点数对热边界条件反演结果的影响。其中,当M=1时,温度测点取T3;当M=2时,温度测点取T2和T4;当M=5时,温度测点取T1～T5。对应的结果见图10、图11和表4。

图10 不同测点数下q1(t)的反演结果

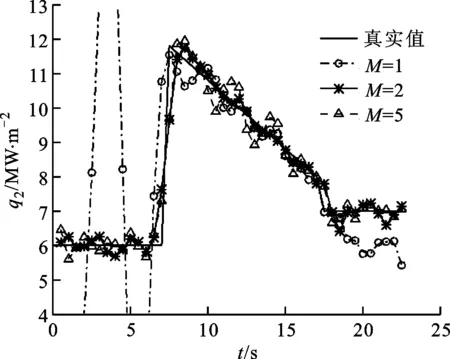
图11 不同测点数下q2(t)的反演结果

当M=1时,测点位置离初始和结束时的热边界较远,对应的阶跃响应系数较小,使得在钻削起始段和结束段的热流反演结果较差。在钻削方向上增加温度测点数,可以明显改善热流的反演结果。对于本文工件的钻削深度而言,M=2,5时的反演结果相差不大。

表4 不同测点数下的反演误差

3.6 未来时间步数的影响

采用测点T2和T4的温度信息,在σ=0.01、v=0.002 m/s的条件下,分别取R=3,6,9来讨论未来时间步数的选取对反演结果的影响,对应的结果见图12、图13及表5。

图12 不同未来时间步数下q1(t)的反演结果

图13 不同未来时间步数下q2(t)的反演结果

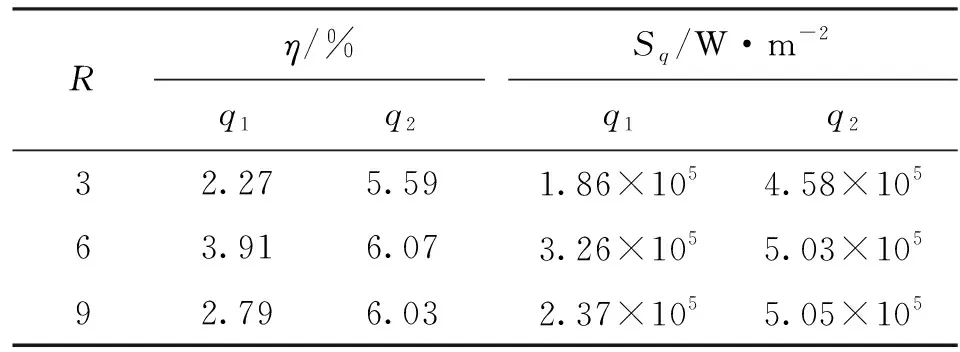
Rη/%q1q2Sq/W·m-2q1q232.275.591.86×1054.58×10563.916.073.26×1055.03×10592.796.032.37×1055.05×105

由图12、图13及表5可知,采用本文的模型预测反演方法,在不同的未来时间步数下均能够获得较为满意的结果,降低了移动边界热流反演结果对于未来时间步数的依赖性。

4 结 论

本文采用模型预测控制方法研究了钻孔工件移动边界热流的反演以及温度场重构的问题,并讨论了钻具进给速度、温度测量误差、测点数等对边界热流反演结果的影响,得到的主要结论如下。

(1)本文建立的反演方案能够有效反演钻孔工件的移动热边界条件,为钻孔工件瞬态温度场的在线重构提供了一种解决方案。

(2)当测量温度数据存在一定的误差时,本文的模型预测控制方案仍然可以获得较为满意的反演结果,表明该方案具有一定的抗干扰能力。

(3)由于不需要对未来一段时间内移动热边界条件的变化进行假设,使得本文的模型预测反演方案降低了反演结果对于未来时间步数的依赖性。