求解滑移流区外掠圆柱体气流流动与传热特性的数值模型

谢福寿,雷刚,邱一男,徐元元,王天祥,厉彦忠

(1.航天低温推进剂技术国家重点实验室,100028,北京;2.西安交通大学能源与动力工程学院,710049,西安)

近年来,关于稀薄气体流动与传热问题日益受到人们的关注,最典型的4类案例为:①运载器穿过大气层或再入大气层的气动加热[1];②火星登陆器热设计和热管理[2];③微小精密热线风速仪研制[3];④高速真空隧道内列车仪表的热设计和热管理[4]。对于运载火箭升空,随着大气密度的逐渐减小,气体的稀薄效应开始凸显,连续介质假设逐渐失效,此时气体流态会依次经历连续流区(Kn<10-2)、滑移流区(10-210),如图1所示。目前,由于稀薄气体流动复杂,致使无法采用统一的算法或方程进行描述,故每个流态的求解方法不尽相同。

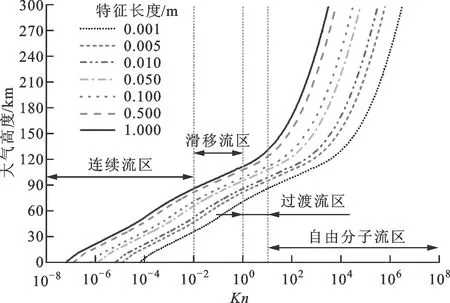
(a)不同特征长度下气体流态划分

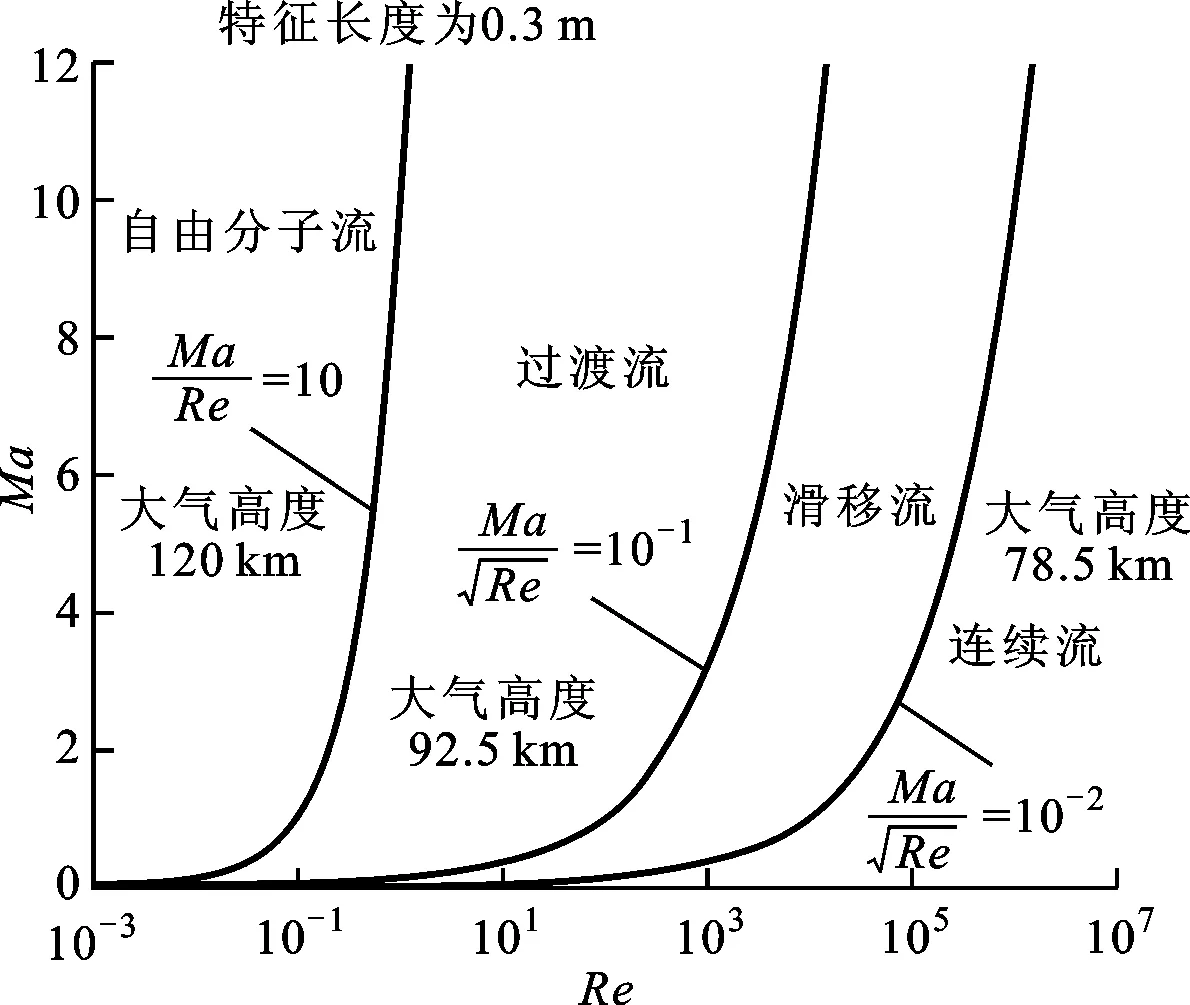
(b)不同马赫数和雷诺数下气体流态划分图1 运载火箭穿越大气层时气体流态随大气高度的分布

滑移流区是指气体与气体之间的碰撞频率,虽然其比气体与物体表面间的碰撞频率高相当多,但稀薄效应已不能再忽略,在靠近壁面处的非平衡效应开始占主导作用,此时气体流动与传热会呈现出两个典型的特征:①速度滑移;②温度跳跃。为了充分反映出该流域的典型特征,许多研究者采用壁面边界条件修正的CFD技术进行流动与传热研究[5-10]。Kishore等通过速度滑移和定壁温边界条件修正对牛顿流体外掠球形颗粒的传热现象进行了数值仿真[5-6]。Choi等开发了嵌入Maxwell滑移边界条件的非结构化网格N-S方程求解模型,对圆柱体表面的速度滑移和温度跳跃进行了研究[7]。索晓娜等采用连续介质流动方程与壁面速度滑移和温度跳跃边界条件相结合描述微通道内稀薄气体二维可压缩滑移流动[10]。Xie等对滑移流区稀薄空气外掠圆柱体流动与传热特性展开了研究,其雷诺数范围为0.001～20,克努森数范围为0.01～0.1[11]。虽然许多学者针对滑移流区采用N-S方程进行了一定的研究,然而都没有考虑壁面曲率对速度滑移和温度跳跃的影响以及滑移边界方程与CFD求解器之间坐标系的转换。Lockerby指出在目前稀薄气体流动中,Maxwell最初滑移边界条件被广泛地误用,其认为假如采用通用滑移边界来模拟带曲率的壁面问题时,一些关键的物理现象就会丢失:①通用滑移边界条件计算出的切向滑移速度明显低于Maxwell最初滑移条件得出的;②对于带曲率的弯头通道,采用Maxwell最初滑移边界可以预测速度逆流现象,而通用滑移边界条件则不能预测该流动行为;③对于外掠一个理想光滑球体,假定所有的入射分子都发生镜面反射,即α=0,则采用Maxwell最初滑移边界推导的Basset阻力方程预测表面摩擦阻力系数应该为0,但采用通用滑移边界条件推导的方程预测结果为负值,出现了非物理解[12]。

课题组前期搭建了一套低密度风洞试验装置,开展了大量的实验研究,获得了一些有价值的研究结果[13-14]。然而,这些实验结果并不能形象地展示出流场和温度场的变化规律。当克努森数增加时,也不能获得压力系数和传热系数沿圆柱体壁面变化的规律,更不能揭示流体掠过圆柱体流动与传热的机理。同时,由于实验条件的限制,对总结出的经验关联式,其雷诺数使用范围仍然比较窄。因此,有必要开发新的数值模型来深入研究滑移流区流体流动与传热问题。

为了精确预测滑移流区稀薄气体流动与传热问题,本文拟基于有限容积法的ANSYS FLUENT 18.0平台,开发一套可用于该流域气体外掠圆柱体流动与传热仿真的数值模型,其考虑壁面曲率的影响,解决了CFD求解器中一些关键性技术问题,如坐标变换、UDF开发、UDF植入、求解发散等。在此基础上,与课题组之前实验数据进行详细的对比验证,充分验证数值模型的可靠性和精确度,为计算流体动力学实现滑移流区气体流动与传热问题研究构建一座桥梁。

1 数值模型构建

本文所研究的问题为稀薄气体外掠圆柱体,直径为D,流态区域尺寸及坐标如图2所示。圆柱体壁面温度定义为Tw,空气与圆柱体之间的温度跳跃和速度滑移定义为Ts和us。

图2 计算区域与边界条件示意图

1.1 层流N-S控制方程

对于滑移流区,气体横掠圆柱体在主流区的流动和传热现象可由N-S方程和能量方程来描述,其中二维、层流、不可压缩流体的无量纲表达式如下

(1)

(2)

(3)

(4)

式中:u*、v*分别为x、y方向的无量纲速度分量;p*为无量纲压力;T*为无量纲温度。

无量纲变量定义为

式中:u、v分别为x、y方向速度分量;u∞为自由流速度;p为空气压力;ρ∞为气体密度;T为气体温度;T∞为自由流温度;Cp为压力系数;p∞为自由流静压力;Cf为表面摩擦系数;τw为壁面剪切力。

1.2 边界条件

滑移流区气体横掠圆柱体流动与传热问题的边界条件如图2所示,详细设置如下。

在计算区域左侧,均匀的速度入口边界条件和气体温度设置为

u*=1;v*=0;T*=0

在计算区域右侧,默认气体在出口处为充分发展状态,压力出口边界条件和空气温度设置为

沿着计算区域顶端和底端,壁面设置为移动壁面,速度等于入口速度,即

u*=1;v*=0;T*=0

在圆柱体壁面,速度滑移表达式以速度分量的形式植入到移动壁面中,其具体的表达式为[15]

(5)

式中:un为壁面法向的气体速度;n为壁面法向的坐标;s为壁面切向的坐标;σm为动量协调系数,具体取值见1.3小节;Lm为气体分子平均自由程。方程(5)右侧第1项是一阶等温速度滑移,由圆柱体壁面处的切向应力推导而来,而第2项是由于切向温度梯度引起的一个热蠕动。需要说明的是,在带曲率的物体中应将导数项∂un/∂s考虑进去,然而在大多数已公布的工作中,该项要么被忽略,要么被导数项∂us/∂s错误地取代。Lockerby研究发现,将导数项∂un/∂s代入滑移边界方程之中,对于越稀薄的气体,计算越准确[12]。

温度跳跃的表达式以壁面温度修正的形式植入到壁面中,其具体的表达式为

(6)

式中:a为热协调系数,具体取值见1.3小节。

1.3 壁面边界条件滑移修正

速度滑移边界条件以一个移动壁面速度的形式加入,而温度跳跃的边界条件则以一个修正的定壁温形式添加。该UDF采用C语言来编写,以编译的形式在Fluent求解器中执行,其中所涉及到的速度梯度和温度梯度分别从求解器中抽取,而速度滑移和温度跳跃根据方程(5)(6)计算得到。

由于圆柱体表面存在曲率,所以自然坐标系与求解器中默认的笛卡尔坐标系是不统一的,正如图3所示。为了表达自然坐标系(s,n)中速度向量和所有的导数项,必须进行坐标变换。笛卡尔坐标系(x,y)中速度向量和所有的导数项可以从Fluent求解器中抽取。在坐标变换之前,首先必须确定在壁面每个单元上两个坐标系之间的夹角θ。根据空间向量的性质,通过余弦函数则可以给出θ的表达式

(7)

式中:A=-An为边界单元面积的法向向量,由Fluent®求解器提供;i、j为沿着x、y方向的单位向量。

图3 在壁面处笛卡尔坐标系与自然坐标系及速度分量

使用链式法则,可将方程(5)(6)的导数项表示为

(8)

(9)

(10)

(11)

自然坐标系与笛卡尔坐标系关系如下

(12)

在s、n方向对x、y分别求偏导数的表达式为

(13)

在笛卡尔坐标系和自然坐标系中,向量u可分别表达为

uxi+uyj

(14)

usk+ung

(15)

式中:k和g为s、n方向上的单位向量。

根据几何关系,如4所示,可获得向量(i,j)和(k,g)之间的关系如下

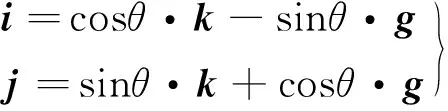
(16)

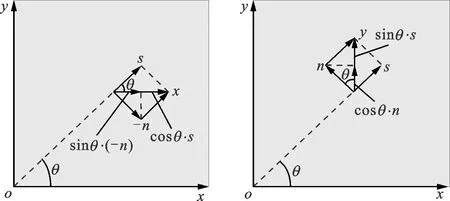
(a)自然坐标系对i的表达 (b)自然坐标系对j的表达图4 单位向量变换

最后,将方程(16)代入方程(14),化解整理后,即可得到(ux,uy)和(us,un)之间的关系为

u=(uxcosθ+uysinθ)k+(-uxsinθ+uycosθ)g

(17)

于是

(18)

将方程(13)(18)代入方程(8)～方程(11),所有的导数项即可整理为

(19)

(20)

(21)

(22)

通过访问ANSYS Fluent求解器中的数据内存,可获得速度和温度的全部偏导数项(∂ux/∂x,∂ux/∂y,∂uy/∂x,∂uy/∂y,∂T/∂x,∂T/∂y)。对于角度偏导数(∂θ/∂x和∂θ/∂y),则需要通过极坐标系来确定。

如图5所示,笛卡尔坐标系中(x,y)与极坐标系中(r,θ)之间的关系可依据几何关系来表示

(23)

式中r为圆的半径。于是,角度偏导数可表示为

(24)

图5 笛卡尔坐标系与极坐标系之间的变换

需要说明的是,动量协调系数σm和热协调系数a一般取决于许多因素,如气体与物体表面材料的种类、壁面光滑度、表面的清洁程度(氧化程度、是否有污染物覆盖、是否吸附其他气体)、温度、压力等以及一些尚未被人们知晓的因素,且两个系数都在0(镜面反射)到1(漫反射)之间变化。根据文献[16-17]报道,对于大多数工程应用来说,这两个系数都非常接近于1,故在目前的工作中这两个系数都取为1。

1.4 CFD数值计算方案确定

采用商业计算流体动力学代码——ANYSYS Fluent展开数值仿真,即联合边界条件求解控制方程(1)～方程(4),最终获得了稀薄气体外掠圆柱体的压力场、速度场和温度场。空间离散梯度方案选择基于单元最小二乘法梯度,压力离散方案选择二阶格式,动量方程和能量方程离散方案选择二阶迎风格式。在Fluent中,默认收敛标准是足以用来判断收敛的,即连续方程和动量方程的全局残差均降到了10-11,而能量方程的全局残差降到了10-15,则认为迭代收敛。

2 结果讨论与分析

2.1 连续流低压状态下定克努森数结果比较

图6展示了连续流区低压状态下无滑移边界数值预测值与滑移边界数值预测值的比较结果,其中低压状态的压力为50 kPa,所对应的克努森数为0.006。从图中对比可知,只要气体流态处于连续流区时,无论是常压状态还是低压状态,无滑移边界与滑移边界的计算结果都非常相近,两者相对误差在1.5%以内。

图6 连续流区数值计算结果

2.2 滑移流区低压状态下定克努森数结果比较

图7呈现了在滑移流区状态下无滑移边界数值预测值、滑移边界数值预测值和实验结果的对比。滑移流区低压状态分别是指气压压力为6 kPa和3 kPa,所对应的克努森数分别为0.054和0.108。从图中可看出,当气体流态由连续流区进入到滑移流区后,采用无滑移边界条件的计算结果与实验结果的误差已达到±15%,尤其是压力越低,克努森数越大,计算误差越大。即使在同一压力下,采用无滑移边界条件的计算结果与实验结果的误差也会随着雷诺数增大而增大。采用滑移边界条件的计算结果可将误差控制在±2.5%以内,所以在稀薄气体滑移区的流动换热问题中,本文修正的滑移流区数值模型可保障数值计算的准确性。

(a)6 kPa

(b)3 kPa图7 滑移流区数值计算结果

2.3 过渡流区低压状态下定克努森数结果比较

图8给出了过渡流区状态下无滑移边界数值预测值、滑移边界数值预测值和实验结果的对比。过渡流区低压状态是指气体压力为1 kPa,所对应的克努森数为0.323。从图中可看出,当低压气体的流态处于过渡流区时,采用无滑移边界条件的计算结果与实验结果的相对误差已达到±60%,即使采用滑移边界条件修正,也只能将相对误差缩小到±20%以内。

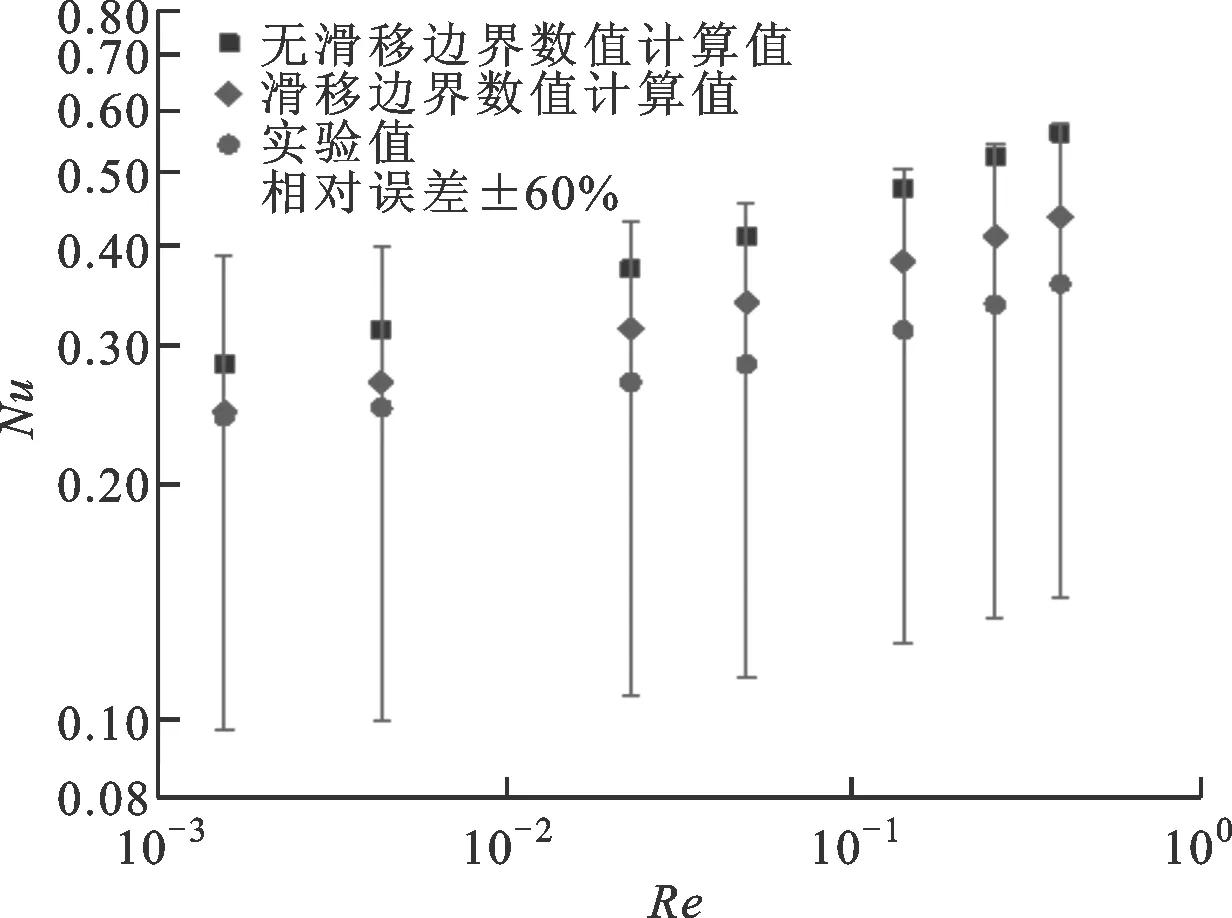
图8 过渡流区数值计算结果

2.4 跨流域变克努森数结果比较

为了进一步验证该数值模型的可靠性和精确度,维持气体速度(3 m/s)不变,通过改变气体压力,使压力在100 Pa～100 kPa之间变化,获得了数值预测值、实验值,并与传统经验关联式(Fand[18],Hilpert[19],McAdams[20],Collis[21])预测值进行了比较,如图9所示。从图中可清楚地看到,在连续流区,数值计算结果与本文实验值、Collis的经验关联式预测值和Fand的经验关联式预测值都吻合良好,说明数值计算过程都是合理的,包括边界条件设置、求解方法选择、物性设置、区域无关性研究和网格无关性研究等。

图9 跨流域变克努森数结果比较

在滑移流区,采用滑移边界条件修正的数值计算结果与本文实验值吻合良好,其最大相对偏差处于±2.5%以内,而采用无滑移边界条件的数值计算结果逐渐偏离实验值,最终达到10%的相对偏差。也就是说,通过滑移边界条件修正,数值计算结果的精度有了显著提升。

在过渡流区,采用滑移边界条件修正的数值计算结果与本文实验结果相比,计算偏差逐渐增加,而采用无滑移边界条件的数值计算结果则完全偏离了本文实验结果,因此在该流态下,数值计算模型需要进一步修正。然而,本文侧重于滑移流区低压空气外掠圆柱体流动与传热特性研究,所以在此不考虑过渡流区。

2.5 滑移效应对低压气体外掠圆柱体的流动影响

图10展现了在滑移流区当雷诺数为1时无量纲滑移速度沿圆柱体壁面的分布规律。从图中可看出,当克努森数保持不变时,无量纲滑移速度在前止滞点处为0,随着角度α的增加,其逐渐增加到某一最大值,然后开始减小,直到在后止滞点处变为0。因为在前止滞点处,空气动压转变为静压,使速度变为0。随后,静压会逐渐再次转变为动压,使壁面的切向速度最终达到一个最大值。由于稀薄效应的影响,最大无量纲滑移速度会随着克努森数的增加而增大,当克努森数达到0.1时,最大无量纲滑移速度可达到自由来流速度的16%。

图10 无量纲滑移速度沿圆柱体壁面的分布

图11描述了在滑移流区雷诺数为1时压力系数沿圆柱体壁面的分布规律。当克努森数保持不变时,压力系数最大值位于圆柱体前止滞点处,且沿着圆柱体壁面逐渐减小。然而,由于滑移效应的影响,圆柱体前止滞点处的压力系数会随着克努森数的增加而逐渐减小,不过克努森数对压力系数的影响其实并不大。

图12 表面摩擦系数沿圆柱体壁面的分布

图12描述了在滑移流区雷诺数为1时表面摩擦系数沿圆柱体壁面的分布规律。从图中可知,当克努森数一定时,由于雷诺数较低,黏性力起主导作用,从而抑制边界层分离,使圆柱体前止滞点与后止滞点速度为0,故表面摩擦系数沿着圆柱体壁面先从0增加至最大值,然后逐渐减小至0。由于稀薄效应影响,最大表面摩擦系数随着克努森数增加而逐渐减小,当克努森数达到0.1时,最大表面摩擦系数比连续流区最大表面摩擦系数减小了38%。

3 结 论

针对滑移流区气体外掠圆柱体问题,构建了一套预测低压气体流动与传热的数值模型,考虑了轴向温度梯度引起的热蠕动影响和壁面曲率的影响,通过与实验数据对比,得出以下结论:

(1)当气体流态处于连续流区时,滑移边界修正模型的计算结果与无滑移边界的计算结果相近;

(2)当气体流态处于滑移流区时,预测外掠圆柱体传热的传统经验关联式已不再适用,此时采用滑移边界修正的数值模型,可实现对稀薄气体滑移流区流动与换热的精确预测,且数值计算结果明显优于传统经验关联式预测结果;

(3)在滑移流区,稀薄效应对低压气体外掠圆柱体的流体动力学特性影响显著,随着克努森数增加,最大无量纲滑移速度呈线性增加,而最大表面摩擦系数呈现线性减小。