低温管路预冷过程两相流动与换热计算研究

王娇娇,陈虹,厉彦忠,,王磊,李翠

(1.西安交通大学能源与动力工程学院,710049,西安;2.航天低温推进剂技术国家重点实验室,100028,北京)

近年来低温流体的应用日益广泛,液化天然气(LNG)、液氧(LOX)、液氮(LN2)、液氢(LH2)和液氦(LHe)等经常作为燃料或冷却剂广泛应用于各行业。液氢、液氧具有高比冲、大推力、无毒无污染等优点,被认为是未来深空探测的首选推进剂,然而由于其饱和温度低、气化潜热小,与外部环境温差较大,在运输及使用过程中极易发生剧烈气化。因此,在低温流体传输、加注之前需进行小流量预冷加注,将管路从室温降至低温区。在此过程中,降低预冷时间和减少低温推进剂消耗量具有重要的意义。因此,为了实现预冷过程的准确控制并最大限度地减少低温液体消耗,需对预冷过程的瞬态热传递机制开展深入研究。

由于管壁与流体温差较大、压力和速度波动剧烈以及复杂的两相流动与换热,使得相关研究面临较大挑战,低温流体预冷管路沸腾换热主要依靠实验研究。近年来,研究人员针对液氮预冷沸腾开展了大量实验研究,为减少复杂性,研究者通常把预冷沸腾的各种影响因素孤立起来进行实验,进而分析各因素对过程发展的影响和作用机制[1]。Velat等指出质量流速是预冷过程重要的影响因素[2-3],Hu等分别进行不同方向预冷实验,发现竖直向上管路预冷速度快于竖直向下[4]。Shaeffer等研究了流动方式的影响,得到间歇流动方式利于减少推进剂消耗量[5]。Hartwig等研究了工质对流动沸腾的影响[6]。在此基础上,Darr等对液氮管路流动沸腾开展大量的实验研究,为理论分析和机理研究提供了大量数据[7-10]。目前,预冷沸腾方面的相关理论研究较少,主要沿用传统两相流动与换热理论。Chung等建立的两流体模型在一定条件下与实验结果比较符合[11-13]。孙恒等采用均相模型[14-15],余红梅等采用气液同速推进分层流动模型[16],对低温流体预冷管路过程进行预测,均取得一定进展。

综上所述,由于低温管路预冷沸腾机理的复杂性、随机性、多样性以及非稳态的发展过程,相关研究还很不充分,不确定因素和未知现象较多。因此,本文构建了有效的低温管路预冷模型,利用多个文献中的实验数据验证了模型的有效性,并对预冷过程中的流型与换热特性及非稳态降温特性开展了预测与分析。

1 控制方程

1.1 低温液体流动与换热方程

本文采用一维均相模型描述预冷过程中管内低温流体,将气液两相处理为混合均匀的、具有平流动特性和平均物性的单一流体,假设管流为一维流动,采取准稳态描述方式,两相之间处于热、力平衡。管路中流体流动与换热的控制方程为

连续性方程

式中:ρ为流体密度;A为管路截面积;u为流体速度;t为时间;x为管路轴向坐标。

动量方程

式中:P为压力;fR为摩擦因数;θ为重力场与管流方向夹角;g为重力加速度。

能量方程

式中:γ为焓值;Sh为单元体管路壁面与低温流体间的换热量。

1.2 管壁一维非稳态导热方程

在预冷过程中,管壁温度从室温降至低温区,一维非稳态导热方程(忽略轴向导热)为

式中:ρs为管路壁面固体密度;cp,s为管路壁面热容;λs为管路壁面导热系数;Tw为壁面温度;r为管路径向坐标。

管路内壁面与管内流体对流换热,管路外壁面与外界环境换热,内外壁面边界方程分别为

式中:hconv为内壁面与流体之间换热系数;qpar为外界环境漏热热流。

1.3 真空绝热管路的漏热计算

真空绝热管路的外界环境漏热包括辐射换热和残余气体导热两部分,其中辐射换热可根据斯蒂芬-玻尔兹曼方程计算,即

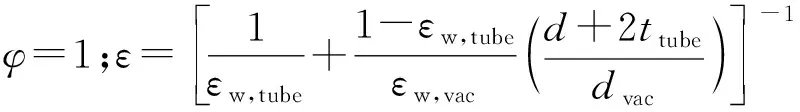
残余气体导热根据下式进行计算

qgc=kβPvam(Tw,vac-Tw)

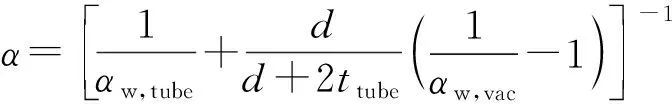
1.4 管壁与流体间的换热计算

图1展示了不同文献中液氮预冷沸腾曲线的实验数据,由图1可知,不同工况的实验结果具有相同趋势,随着壁面过热度的降低,膜态沸腾起始温度TMFB、临界热流CHF、核态沸腾起始温度TONB这3个特征点将流体与管壁间换热依次分为膜态沸腾、过渡沸腾、核态沸腾、单相强制对流4种方式。

由于低温流体物性的特殊性和预冷过程的复杂性,相关研究面临较大挑战。Hartwig等将多个低温预冷实验数据与传统经验关联式进行比较[17],

发

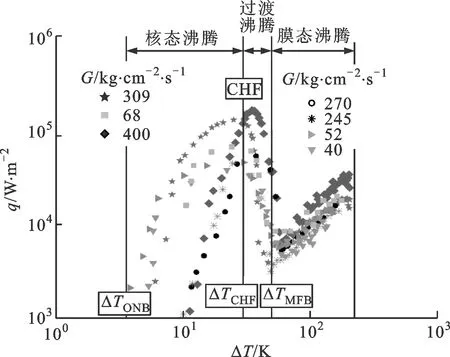
图1 液氮管路预冷过程沸腾曲线

现所有模型与实验数据的误差都非常大,不能预测低温流体预冷管路过程的换热特性。

基于文献中液氮预冷管路的实验数据,本文对3个特征点和4种换热方式的模型分别进行选择,选择结果及与实验数据的对比情况如表1所示。

预冷过程中管内流体依次经历单相气体强制对流、膜态沸腾、过渡沸腾、核态沸腾和单项液体强制对流,不同换热方式分别采用不同公式计算换热系数,如图2所示。若质量含气率大于1或小于0,则流体与壁面间为单相强制对流换热,采用Dittus-Boelter公式或修正的公式。若质量含气率处于0与1之间,则流体与壁面处于两相换热方式。此时根据流量、压力等参数计算膜态沸腾起始点温度TMFB和核态沸腾起始点温度TONB,若壁面温度Tw大于TMFB,则处于膜态沸腾区域,采用Darr膜态沸腾换热公式;若壁面温度Tw小于TONB,则使用Dittus-Boelter公式进行计算;若壁面温度Tw处于TONB与TMFB之间,则流体与壁面之间换热为核态沸腾或过渡沸腾,通过Chen公式计算qNB,修正的Katto公式计算qCHF,若qNB小于qCHF,则处于核态沸腾,采用Chen公式;若qNB大于qCHF,则处于过渡沸腾,采用插值计算。

表1 管壁与低温流体间传热模型

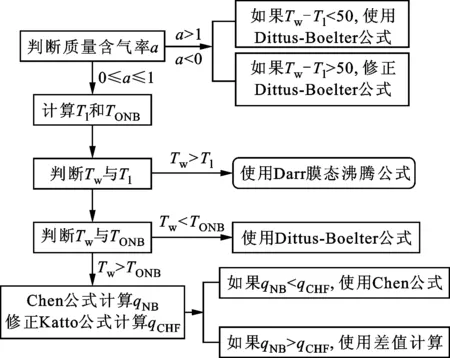
图2 换热模型选择及判定条件

2 计算模型

针对低温流体预冷真空管路过程的管壁瞬态降温特性,采用有限容积法耦合求解管内流体流动与换热方程,有限差分法求解管壁一维非稳态导热方程,流体与壁面的换热通过流型判定及多种换热模型的恰当选用予以考虑,管壁外侧辐射漏热进行线性化离散处理。

2.1 离散化处理

将管路内流体沿长度方向划分节点,管壁沿长度方向和径向均划分节点,离散节点分布如图3所示,其中qcov表示壁面与流体之间换热量。流体流动换热采用有限容积方法进行计算,将含有四次项的辐射热进行泰勒展开,并采用有限差分的方法计算管壁非稳态导热,利用准稳态换热的方法将流固换热以及外界环境漏热进行耦合求解。

热力学含气率x计算式为

式中:γi为节点i处的焓值;γl,sat为饱和液焓;γlv为当前压力下的相变潜热。

每一时刻的流体节点处焓值γi计算式为

γi=γi-1+4qi-1/(πd2G)

式中:γi-1为上一节点焓值;qi-1为上一节点处流体与壁面换热量。

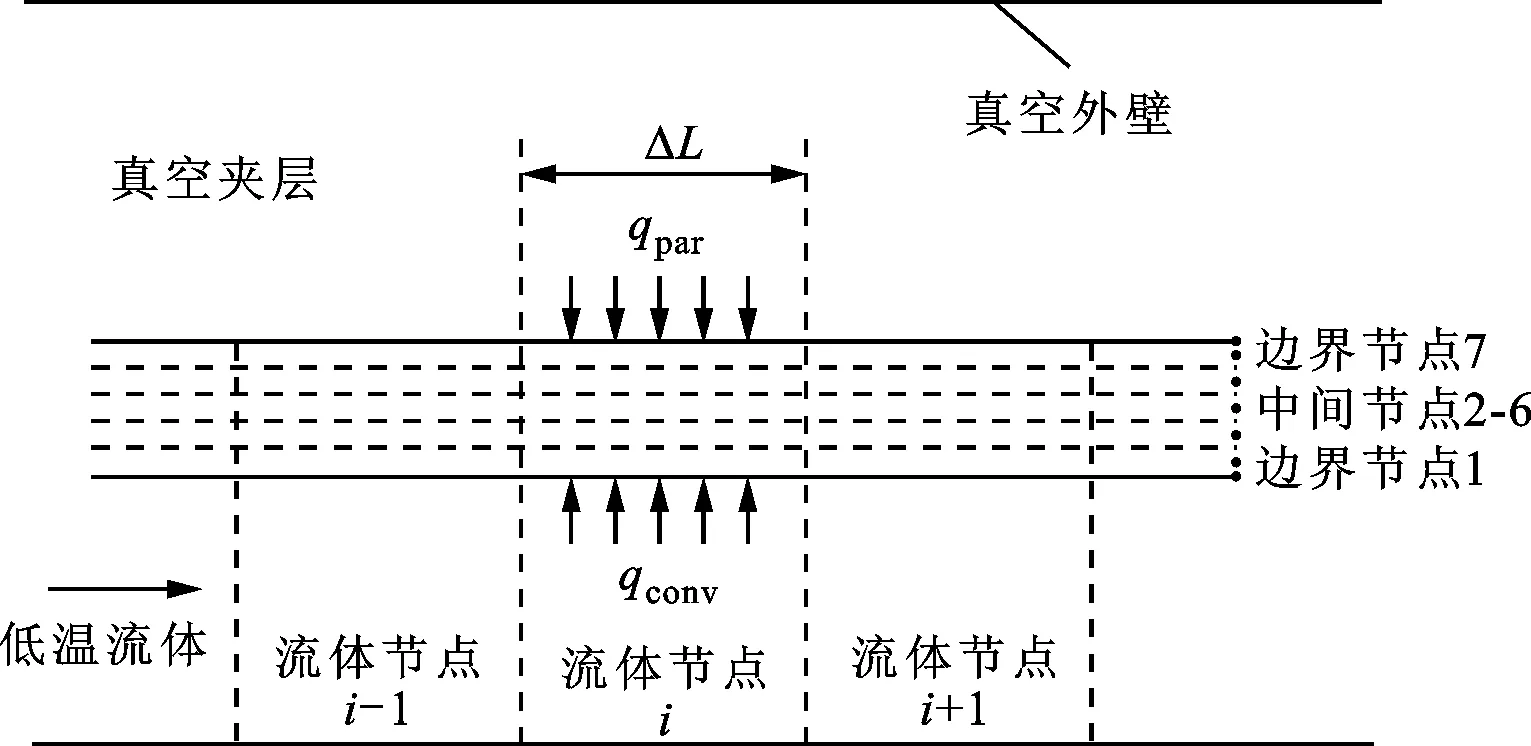
图3 数值模拟离散节点分布

2.2 耦合换热计算

在低温流体预冷真空管路过程中,首先应该判断各节点低温流体与壁面的传热工况,确定流体与壁面间换热量,进而计算出节点处的温度、流速及含气率等流动参数,并计算管壁的温度分布,程序流程如图4所示。

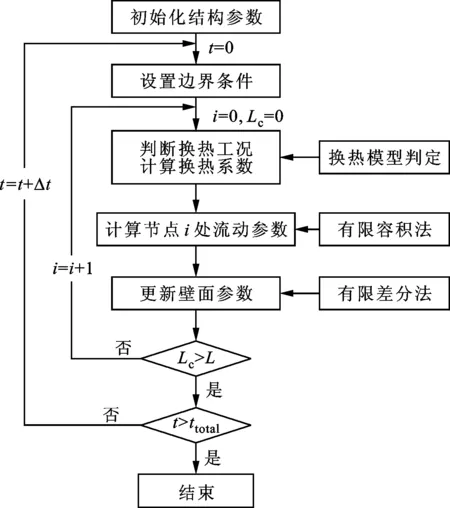
图4 程序流程图

2.3 模型验证

基于上述计算模型,对文献[9]和文献[22]中液氮预冷真空管路的9个实验工况开展计算分析,实验条件如表2所示,其中流动方向包括水平和竖直向下两个方向,9个实验工况的质量流速各不相同。

9个实验工况中预冷时间的实验数据与计算结果的对比情况如图5所示,由图9可知,对预冷时间的预测误差在10%之内,说明本文建立的预冷模型具有较高精度,可用于液氮和液氧(两者物性非常接近)预冷管路的模拟计算中。

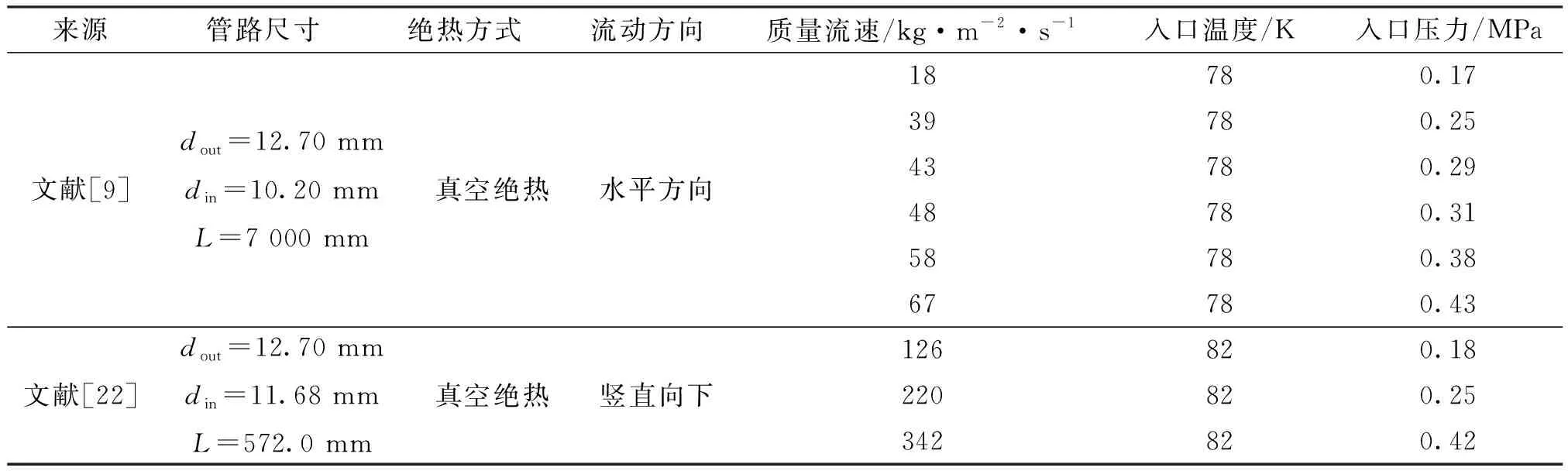
表2 管路预冷实验工况条件

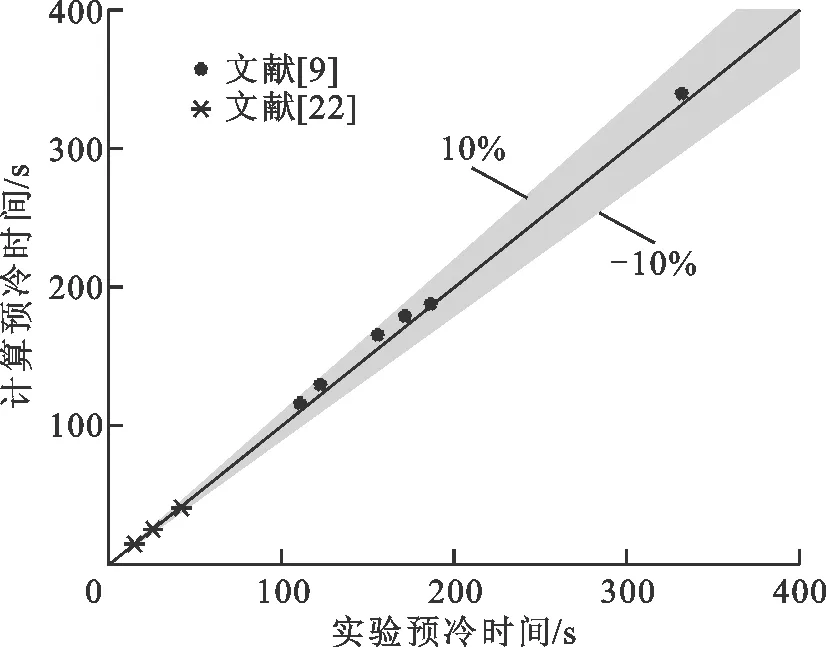
图5 实验数据与计算结果对比

3 管路预冷流型与换热预测及分析

针对文献[9]中G=43 kg/(m2·s)的实验工况,对管路预冷过程中换热特性及流型分布进行预测。

3.1 流型与换热特性分析

70 s时刻管路预冷流型和换热特性情况如图6所示。由图6可知:在70 s时,沿管长方向流型依次为单相液、泡状流、反环状流、单相气,发生的换热方式依次为单相液体强制对流、核态沸腾、过渡沸腾、膜态沸腾及单相气体强制对流;核态沸腾和过渡沸腾换热系数远大于其他换热方式,发生核态和过渡沸腾时,管路中的含气率迅速增大,同时核态、过渡沸腾换热区域远小于膜态沸腾换热区域。

3.2 管壁非稳态温降特性

管路监测点处流体与壁面温度随时间的变化情况如图7所示。由图7可知:首先经历全气相强制对流,壁面温度和流体温度逐渐降低,随后进入膜态沸腾换热,当壁面温度降低为膜态沸腾起始温度时,换热方式变为过渡和核态沸腾,壁面温度大幅降低,随后进入全液相强制对流阶段,直至预冷完成;预冷过程大部分时间为全气相和膜态沸腾阶段,大约占预冷时间的95%以上,核态沸腾和过渡沸腾持续时间很短。

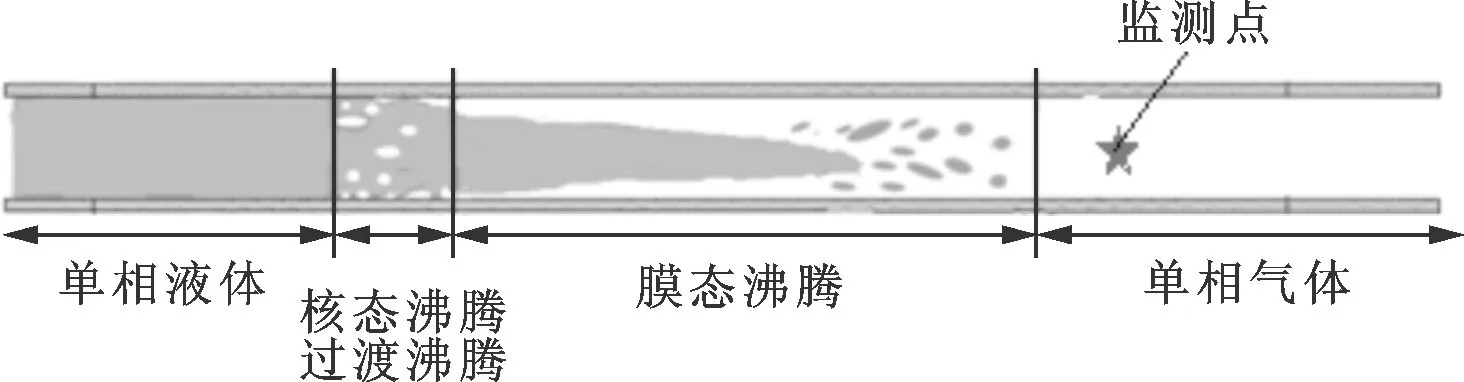
(a)管路预冷流型分布

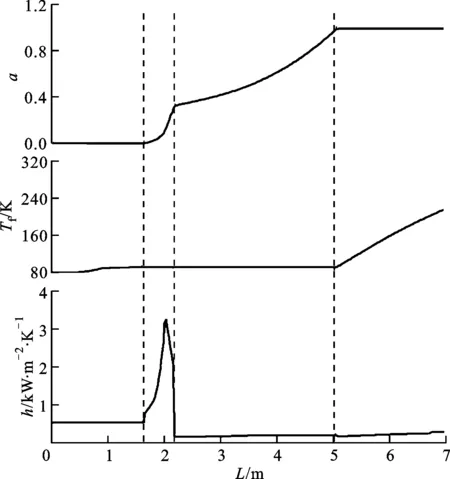
(b)换热特性分布图6 典型时刻管路预冷流型分布及换热特性

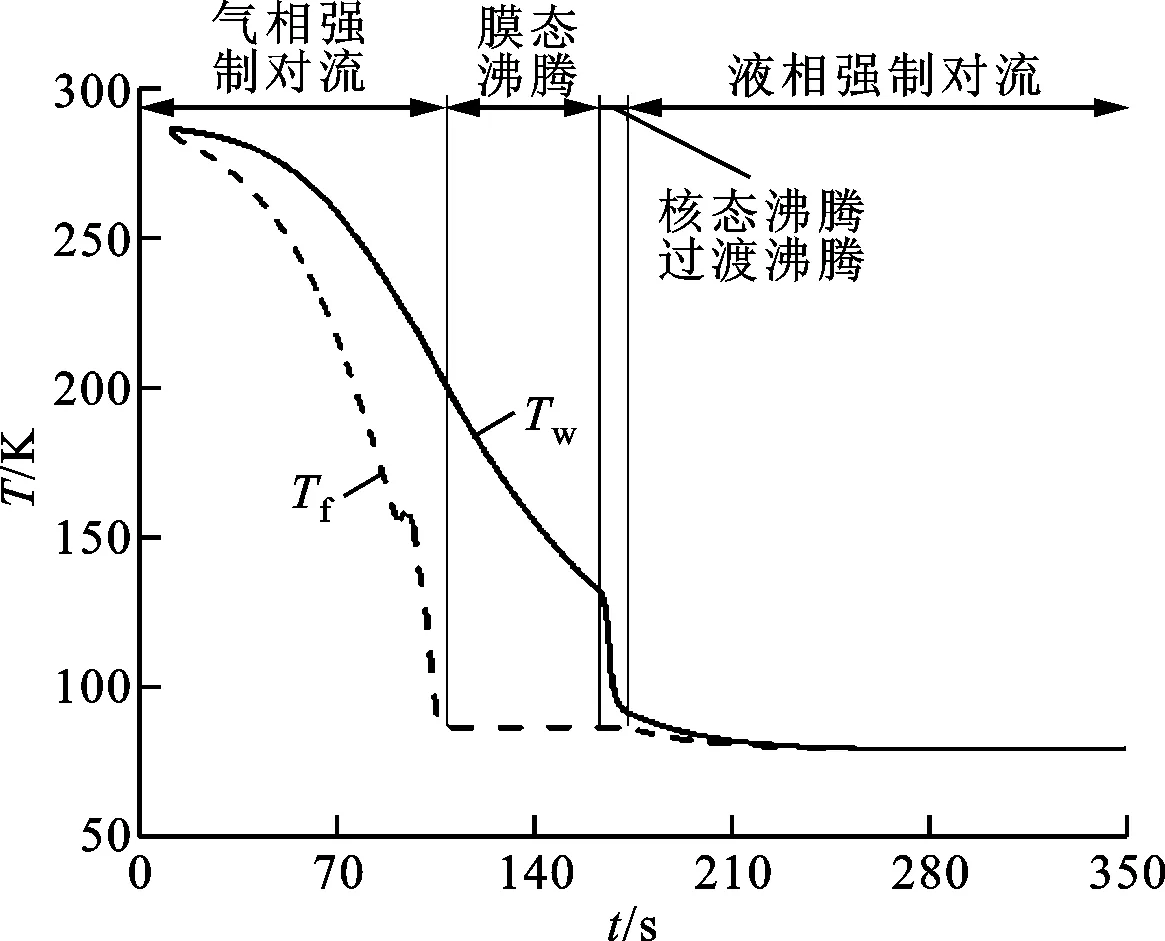
图7 特定位置处流体与壁面温度随时间变化规律

进一步分析整个管路壁面降温特性,沿管路长度方向不同位置处流体温度随时间变化情况和壁面温度随时间变化如图8、图9所示。每个区域中壁面温度随时间及位置以相同规律变化,这是因为相同的换热区域具有相近的换热特性。

此外,距离管路入口2 m内的管路区域,主要发生膜态沸腾,膜态沸腾换热将壁面温度冷却至约130 K,之后核态和过渡沸腾将壁面冷却至流体温度附近。距入口2 m之后的管路区域,先经历气相强制对流,壁面温度降至200 K左右,之后发生膜态沸腾换热,壁面降至130 K附近,最后发生核态、过渡沸腾。由图9可知,壁面温度降低过程的换热量主要通过气相强制对流换热和膜态沸腾,约占总换热量75%。

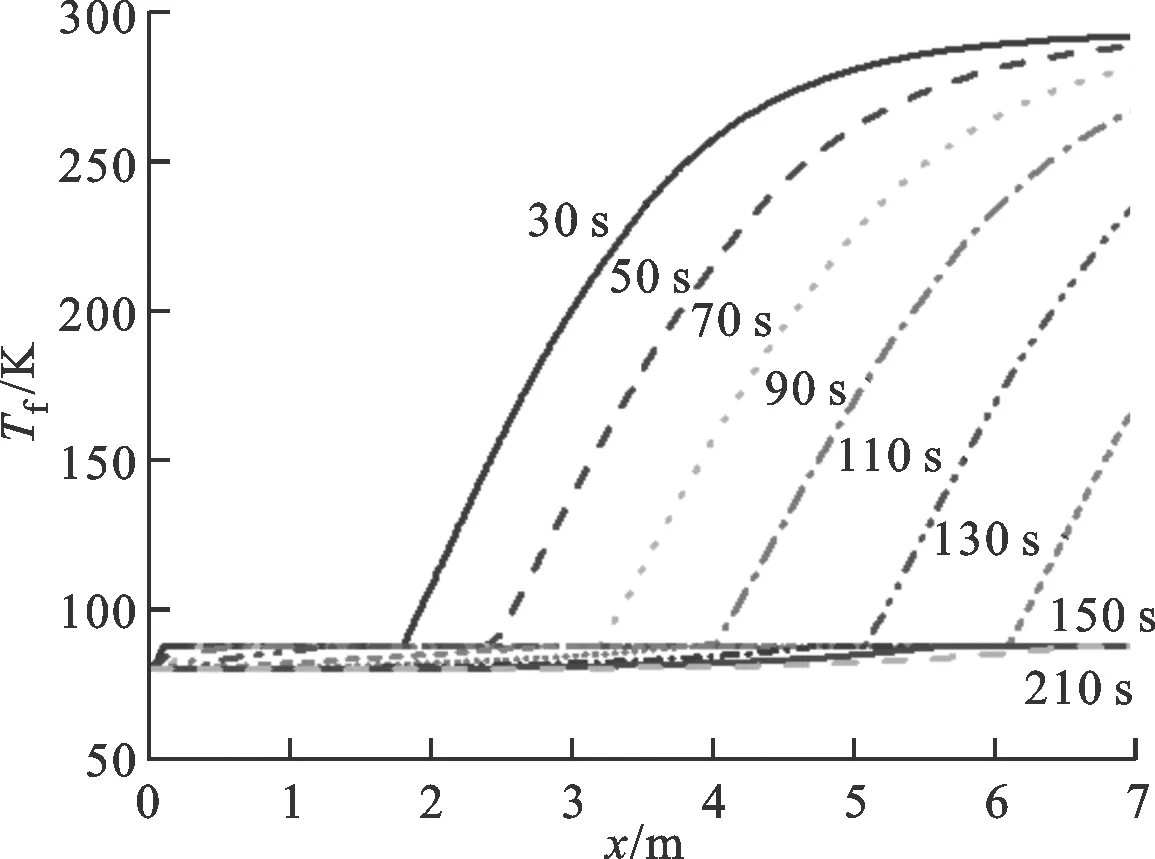
图8 流体温度随时间变化规律

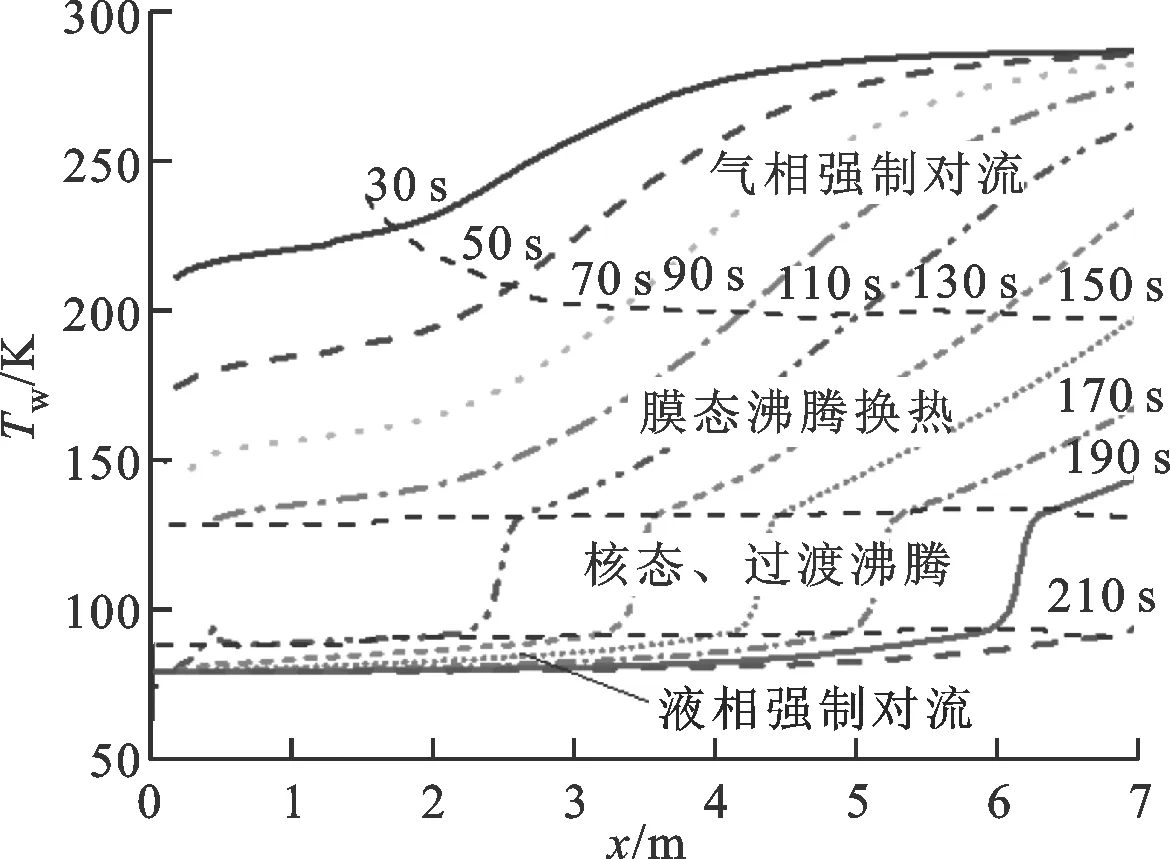
图9 壁面温度随时间变化规律

3.3 质量流速影响分析

为缩短预冷时间同时减少推进剂消耗量,以长度为10 m的管路为模型,将质量流速对预冷过程的影响进行计算分析。质量流速在50 kg/(m2·s-1)和500 kg/(m2·s-1)的范围内,预冷完成时间随质量流速的变化情况如图10所示。由图10可知,质量流速越大,预冷完成时间越短,在低质量流速范围内,预冷完成时间随质量流速的增加而急剧降低,当质量流速增加到一定程度后,预冷完成时间趋于平稳。因此,预冷过程中存在一个最优质量流速,既可以缩短预冷时间,同时也可以减少推进剂的浪费。

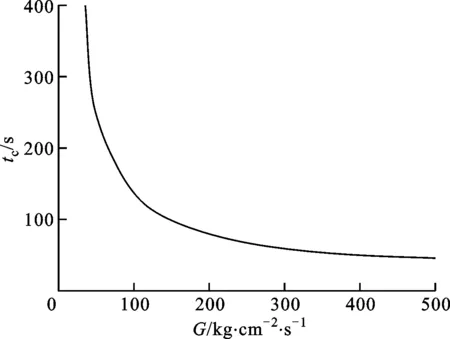
图10 不同质量流速条件下的预冷时间

4 结 论

通过对低温流体预冷管路过程进行计算分析,本文得到如下结论:

(1)本文建立的低温流体预冷真空管路的非稳态计算模型,考虑了预冷过程中多种换热方式,在开展低温流体预冷管路过程预测时具有较高精度,对预冷时间预测的误差在10%之内;

(2)在低温流体预冷管路过程中,不同换热方式的换热情况差异很大,其中核态沸腾与过渡沸腾换热方式的换热系数与其他换热方式相比约大一个数量级;

(3)在低温流体预冷管路过程中,大部分时间的换热方式为单相气强制对流和膜态沸腾,约占总预冷时间的95%,总换热量的75%,核态和过渡沸腾发生时间较短;

(4)质量流速是影响预冷完成时间的重要因素,在低质量流速时,预冷时间随质量流速的增加而迅速降低,当增加到一定程度时,预冷时间趋于平稳。