面向大型航空结构件的混联柔性制造系统概念设计与性能评估

张俊,汤腾飞,方汉良

(福州大学机械工程及自动化学院,350116,福州)

为减轻整机重量,机身、主翼等具有复杂形面的大型航空结构件一般采用铝合金材料,因此该类结构件的加工与装配必须满足严苛的刚度和精度要求。传统的航空制造装配系统一般针对特定工况进行专门设计,容易导致加工柔性差、设计周期长、安装结构繁杂等问题,难以应对产品多样化及市场快速变化的需求[1-2]。因此,研发适用于大型航空结构件的高效、高精度加工的柔性制造系统势在必行[3]。

为提高制造系统的柔性,在航空工业中广泛应用各种工业机器人[4-12]。其中,以Sprint Z3[7]、Tricept[8]、Exechon[9]为代表的并联机器人,因高刚度、高精度、大负载等优点,逐步应用于航空结构件的钻、铣、铆等多种加工与装配场合[10-12]。目前,国外已有公司推出了混联柔性制造系统,如:德国DS Technologies公司的Eco-speed加工中心,采用一个3自由度并联模块串接一个2自由度直线移动导轨,构成5轴混联柔性制造系统,可用于航空结构件的高速铣削[13];西班牙LOXIN集团的Loxin Column Machine,采用Tricept并联机构为核心模块,串接2自由度直线移动导轨,构成多型串并式多轴混联柔性制造系统,可用于航空结构件加工与装配[14]。

然而,由于采用直线式移动导轨,上述制造系统在应对大尺寸弧形结构件时需要多轴运动来合成所需的大尺寸弧形加工轨迹,往往面临工作空间受限、运动控制复杂的局面,难以高效应对机身分段、翼子板等弧形框架式航空结构件的加工与装配。

为解决弧形结构件的制造与装配问题:Oberoi等开发了一款基于弧形导轨的多轴柔性制造系统,并应用于波音777系列的机身钻孔作业[15];浙江大学的Zhu等通过在弧形导轨上串接钻孔机构,构建了一种用于机身钻孔加工的多轴柔性制造系统[16]。

受上述工程问题及相关研究的启发,本文以一类3自由度过约束并联机构为核心功能模块[17],串接弧形导轨,设计了一种5自由度混联柔性制造系统,希望为具有复杂曲面的大型航空结构件的柔性制造与装配提供一种技术解决方案。本文研究从如下方面开展:首先,借助虚拟样机技术进行该类系统的概念设计;其次,开展逆运动学、奇异性建模与分析,以明确该类混联系统的工作空间;再次,通过力能分析,揭示荷载作用下系统各环节的弹性变形;最后,对工作全域内系统力学性能进行全面评估,以揭示位姿参数对力学性能的影响规律。

1 混联柔性制造系统概念设计

1.1 串联模块设计

为适应弧形框架式航空结构件的加工与装配,设计如图1所示的串联模块。

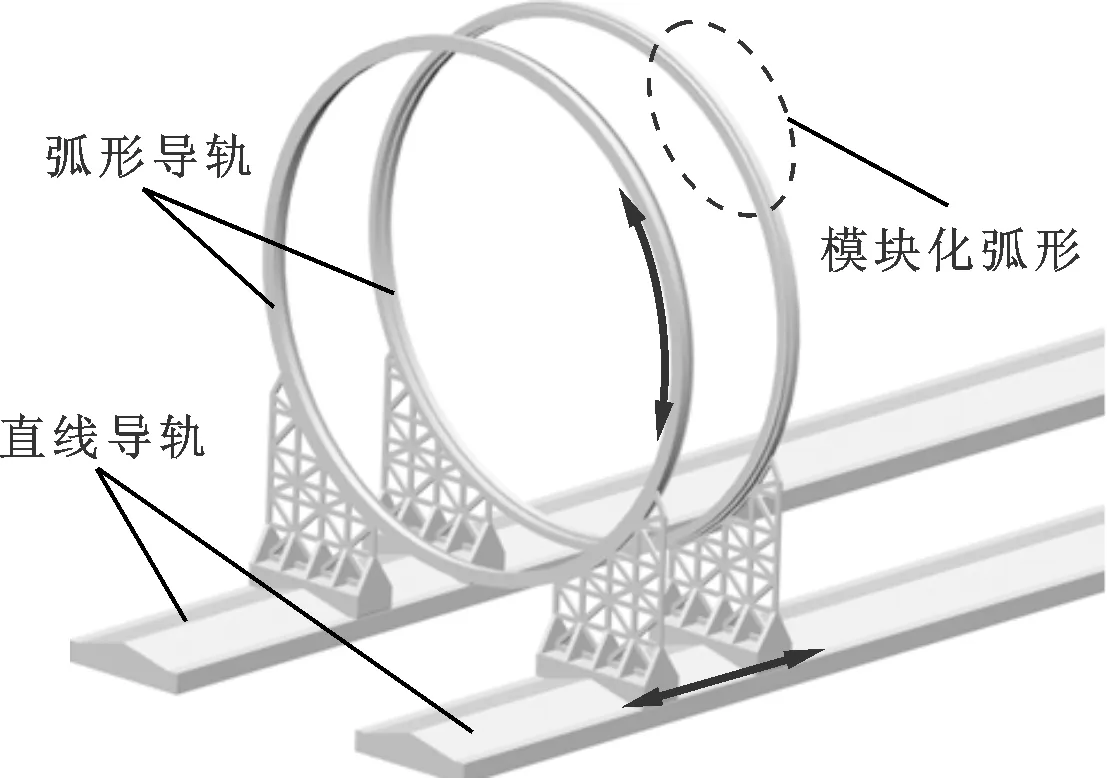
图1 串联模块虚拟样机模型

由图1可知,串联模块主要由一对平行布置的弧形导轨和一对水平安放的直线导轨串联构成。其中,弧形导轨实现绕圆心的转动(1R),直线导轨实现沿导轨方向的移动(1T)。考虑到大尺寸弧形导轨加工困难,可采用多组模块化圆弧段拼装成完整的弧形导轨。

1.2 并联模块设计

为满足航空结构件的加工与装配需求,设计如图2所示的3自由度过约束并联模块,其主要由动平台(含电主轴和操作头)、静平台(含连接结构)和3条驱动支链(含伺服驱动)组成。

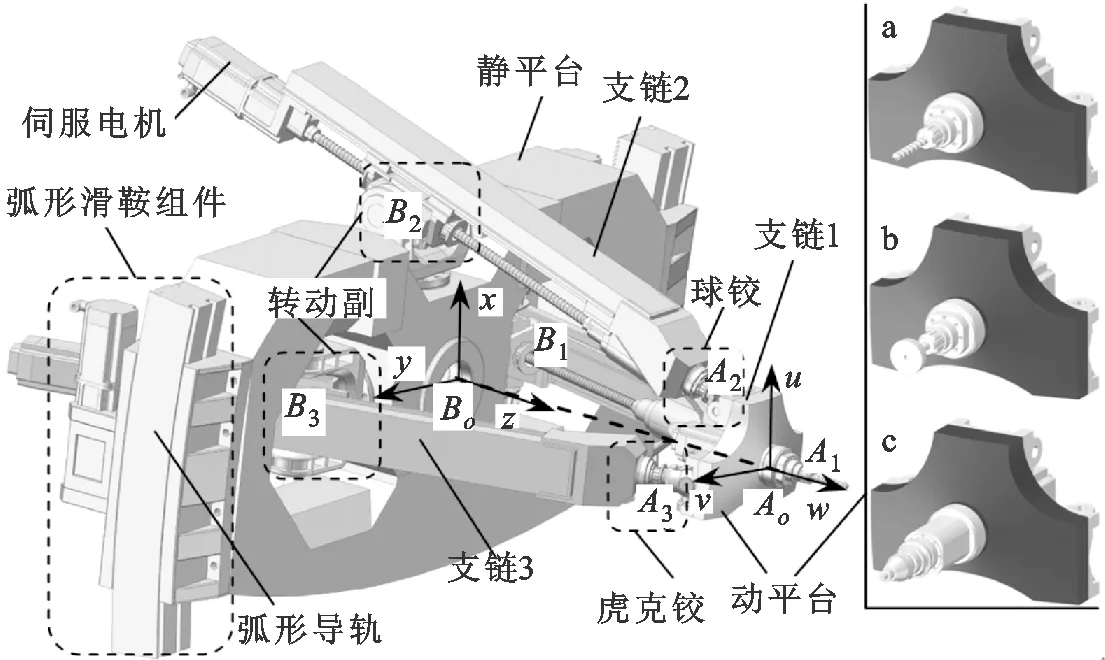
图2 并联模块虚拟样机模型

如图2所示,支链1、3具有相同结构,分别通过虎克铰U(A1、A3)和转动副R(B1、B3)与动、静平台相连,且二者关于支链2对称布置;支链2分别通过球铰S(A2)和转动副R(B2)与动、静平台相连。以机构学的观点分析,该并联模块为2RPU-1RPS过约束并联机构。通过伺服电机驱动3条支链中的主动移动副,可实现动平台绕x、y轴的转动和沿z轴的移动,从而实现两转一平(2R1T)的运动输出[17]。通过在动平台上安装不同的操作机具(如图2中的a、b、c),可实现不同的加工与装配需求,如钻铣、打磨、铆接(配合零件夹持单元)等。

图3为连接结构弧形滑鞍组件的结构设计,其中,主动蜗杆W1驱动从动蜗轮G1转动,进而与G1同轴的齿轮G2驱动与滑鞍固联的从动齿条R2移动。设计蜗杆的导程角小于啮合副的当量摩擦角,以保证并联模块在弧形导轨上运动时自锁。

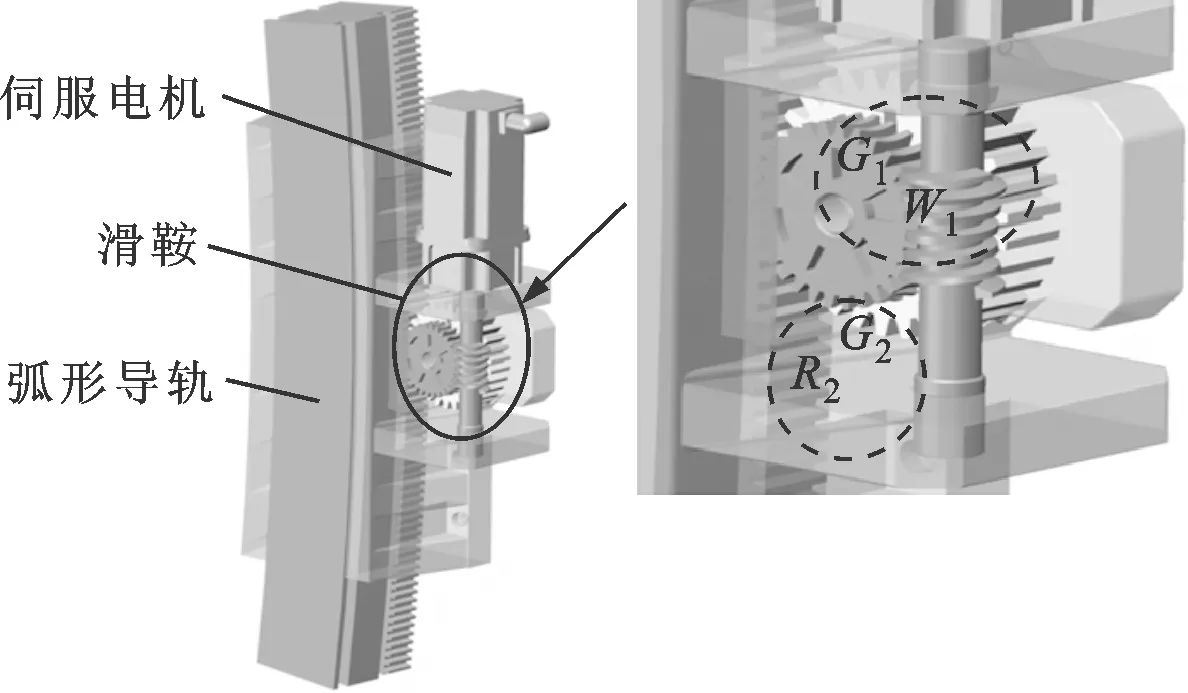
图3 弧形滑鞍组件

1.3 混联柔性制造系统设计

将图1、2所示的串、并联模块结合,可搭建一个类5自由度混联柔性制造系统,如图4所示。

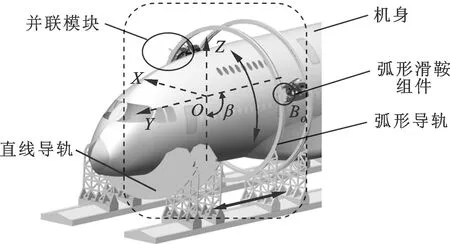
图4 混联柔性制造系统虚拟样机模型

图4中:在双弧形导轨圆心O处建立系统坐标系O-XYZ,并令Y轴指向直线导轨移动方向,Z轴垂直于直线导轨所在平面,X轴由右手定则确定;β表示并联模块在双弧形导轨上绕Y轴的转角,β∈[0,π]。该混联柔性制造系统主要由一转一平(1R1T)2自由度串联模块和2组两转一平(2R1T)3自由度并联模块组成,其中机身由柔性定位工装夹持,2组并联模块通过弧形滑鞍组件安装于串联模块中的双弧形导轨之间,并由滑鞍之上的伺服电动机驱动其沿弧形导轨转动,而直线导轨则由独立的直线驱动模块驱动。

2 运动学分析与工作空间预估

2.1 运动学逆解建模与分析

运动学分析是评估该类混联柔性制造系统工作空间与静力学性能的前提,为此,可建立如图5所示的混联系统运动学模型。

图5 混联系统机构简图

图5中:Ci表示支链i上丝杠后端支承轴承中心;A0表示动平台质心;Ai0表示支链i上的质心;ai和bi分别表示Ai和Bi在Bo-xyz中的位置矢量;ai0表示Ai在Ao-uvw中的位置矢量;a0和li0分别表示A0和Ai0在各自坐标系下的位置矢量;a和li分别表示质心A0和Ai0在Bo-xyz中的位置矢量;r表示动平台坐标中心Ao点的位置矢量;qi和di分别表示支键i的腿长和单位方向矢量;i表示支键编号,i=1,2,3。等腰直角三角形△A1A2A3和△B1B2B3分别表示动、静平台,∠A2=∠B2=90°,外接圆半径分别为rp和rb。

在混联系统的串、并联模块上分别建立以下坐标系:在并联模块动、静平台中心Ao和Bo处分别建立连体坐标系Ao-uvw和Bo-xyz,其中u和x轴分别指向A2、B2,v和y轴分别指向A3、B3,w和z轴由右手定则确定;在支链i的Ai(i=1,2,3)处建立连体坐标系Ai-xiyizi,其中xi平行于x轴,zi沿支链轴线方向,yi由右手定则确定。为清晰计,图5中仅示出支链1的质心A10和支链连体坐标系A1-x1y1z1。

为便于混联系统的运动学分析,可首先分析结构较为复杂的并联模块,并将其运动转换至坐标系Bo-xyz下进行度量,混联系统坐标系O-XYZ相对于并联模块坐标系Bo-xyz的旋转变换矩阵BTO可表示为

(1)

坐标系Ao-uvw和Ai-xiyizi相对于坐标系Bo-xyz的旋转变换矩阵BTA和BTAi可分别表示为

BTA=rot(u,ψ)rot(v,θ)rot(w,φ)

(2)

BTAi=rot(xi,ψi)rot(yi,θi)rot(zi,φi)

(3)

式中:ψ(ψi)、θ(θi)和φ(φi)分别为各自坐标系下的进动角、章动角和自旋角。

在Bo-xyz中,r=(xp,yp,zp)T,其中xp、yp和zp为Ao坐标系分量,且有

r=ai-BTAai0=bi+qidi-BTAai0

i=1,2,3

(4)

类似地,a和li可分别表示为

a=r+BTAa0;li=ai+BTAili0

i=1,2,3

(5)

计入各运动副约束,可得并联模块的连带运动

yp=-rpsinφcosθ;φ=arctan(tanψ/sinθ)

(6)

在并联模块坐标系Bo-xyz下的运动学逆解为

(7)

将式(7)所示的并联模块运动学逆解按照BTO进行相应坐标变换,即得系统坐标系O-XYZ下的混联系统运动学逆解表达。

2.2 奇异性分析

并联模块作为该混联柔性制造系统的核心执行机构,其奇异性是重要的运动学性能参考。

为便于分析,在动平台中心Ao点建立瞬时参考坐标系Ao-u′v′w′,坐标轴u′、v′和w′分别平行于静平台连体坐标系Bo-xyz的坐标轴x、y和z,并根据螺旋理论[18]定义并联模块在瞬时参考坐标系Ao-u′v′w′下的运动螺旋系,如图6所示。

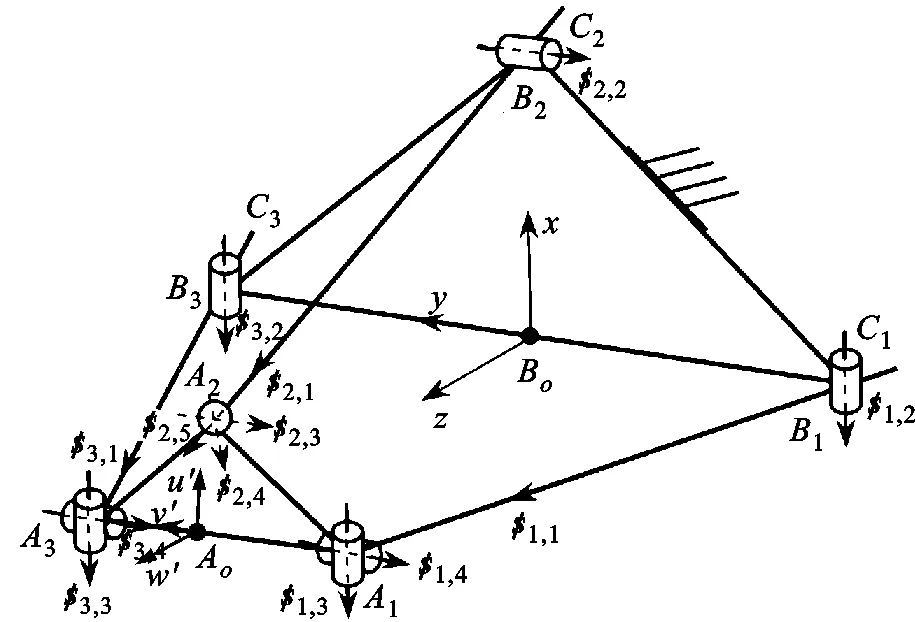
图6 并联模块运动螺旋系

并联模块的动平台由3条支链共同支撑,其在瞬时参考坐标系Ao-u′v′w′下的运动螺旋S/p为

(8)

式中:S/i,p(i=1,2,3)表示瞬时参考系下支链i的瞬时运动螺旋,可分别表示为

(9)

(10)

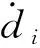
任意位姿下,支链1、3的瞬时运动螺旋系为

(11)

式中:s/i,j表示瞬时参考坐标系Ao-u′v′w′下支链i(i=1,3)上各运动关节中第j(j=1,2,…,5)个转动轴的单位方向向量;rRi和rUi分别表示支链i(i=1,3)上转动副和虎克铰转动中心的位置向量。

对上式求反螺旋,可得支链1、3的约束螺旋系

(12)

式中:s/i(i=1,3)表示平行于s/i,3×s/i,4的单位方向向量。

任意位姿下,支链2的瞬时运动螺旋系为

(13)

式中:s/2,j表示瞬时参考坐标系Ao-u′v′w′下支链2上各运动关节中第j(j=1,2,…,5)个转动轴的单位方向向量;rR2和rS2分别表示支链2上转动副和球铰转动中心的位置向量。

对式(13)求反螺旋,得到支链2的约束螺旋系

(14)

分别将式(12)和式(9)以及式(14)和式(10)做互易积,并结合式(8),改写成矩阵形式为

Jc·S/p=0

(15)

式中:Jc为动平台的约束雅克比矩阵,且有

(16)

(17)

式中:li(i=1,3)表示瞬时参考坐标系Ao-u′v′w′下支链i(i=1,3)上由虎克铰中心指向转动副中心的单位方向向量。

(18)

式中:l2表示瞬时参考坐标系Ao-u′v′w′下支链2上由球铰中心指向转动副中心的单位方向向量。

分别将式(17)和式(9)以及式(18)和式(10)做互易积,并结合式(8),改写成矩阵形式为

(19)

式中:Ja为动平台的驱动雅克比矩阵,且有

(20)

合并式(15)和(19),并改写成矩阵形式为

(21)

式中:J为动平台的全雅克比矩阵,且有

(22)

分析并联模块动平台的全雅克比矩阵J可知:

(1)当单位方向向量l1、l3和l2三者共面时,并联模块处于结构奇异位姿;

(2)由于单位方向向量s/1、s/3,2和s/2,2线性无关,故此类并联模块不存在约束奇异。

2.3 工作空间预估

工作空间是机构设计与分析的关键指标。为明确该混联制造系统的工作空间,在上述机构运动学逆解的基础上,采用“分层切片”思想,提出了系统的工作空间搜索方法,基本流程如图7所示。

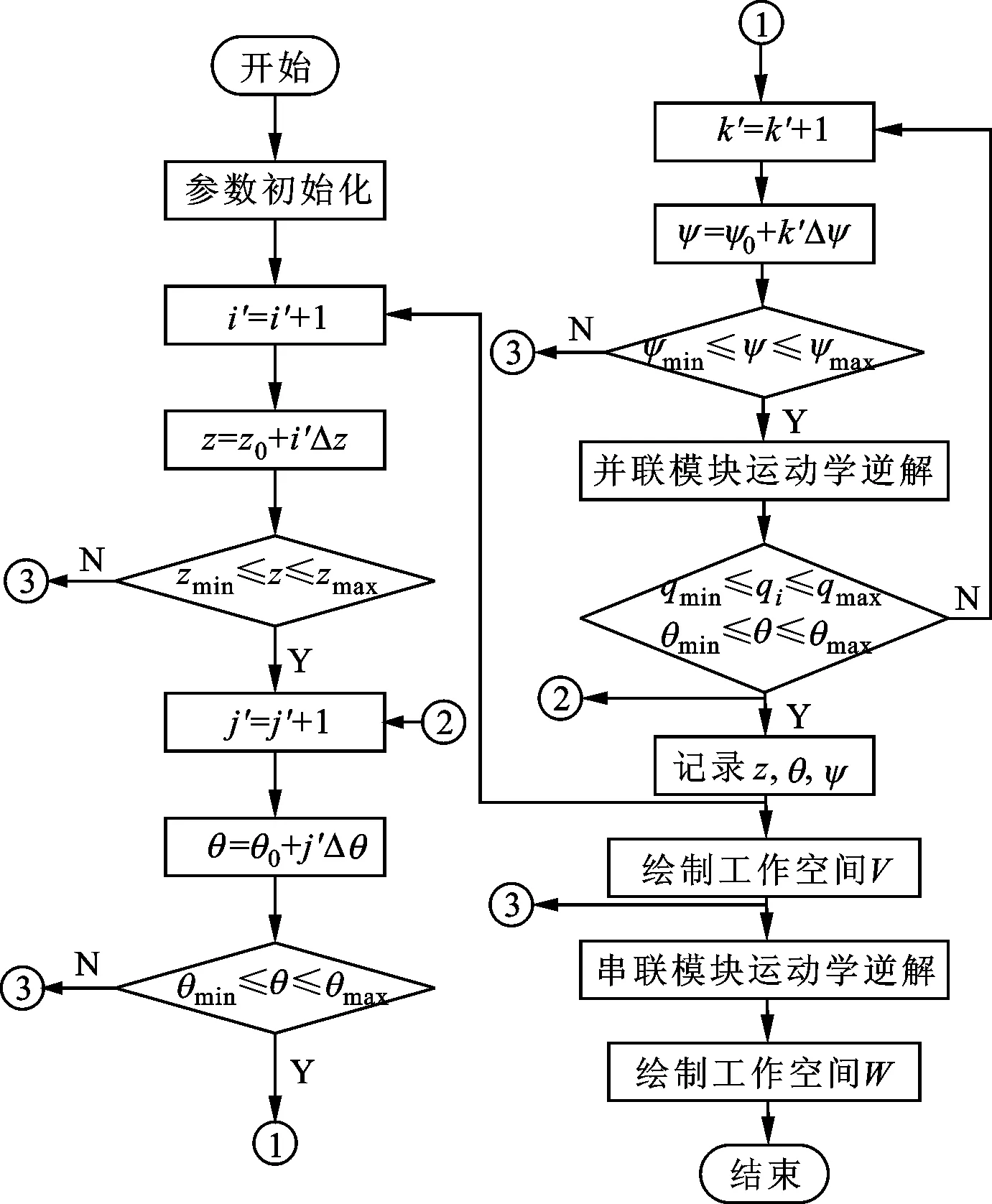
图7 工作空间搜索流程图

参考图7,简述该混联系统的工作空间搜索步骤如下:

(1)在坐标系Bo-xyz下将空间按照z、θ和ψ分别离散成i′、j′和k′份,然后逐个增加i′、j′和k′;

(2)在确定的结构参数下通过并联模块位置逆解求得相关变量,再通过杆长和转角约束条件来判断上述离散点是否为工作空间内的可行点;

(3)将满足约束条件的工作空间可行点一一记录,构成工作空间可行点集,记为并联模块的工作空间V;

(4)类似地,根据坐标系O-XYZ下的运动学逆解,可进一步获得该制造系统的工作空间,记为W。

以图4所示的虚拟样机为例,运用上述方法来预估该类系统的工作空间。该虚拟样机的主要几何参数如表1所示。

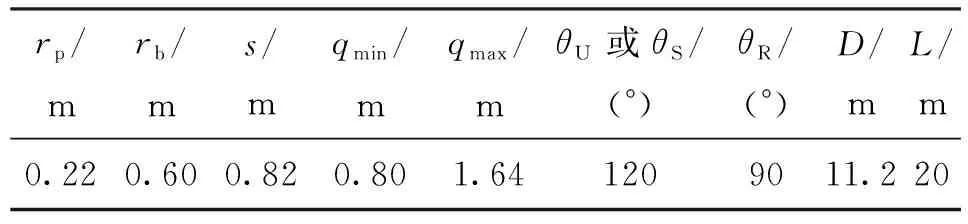
表1 混联柔性制造系统虚拟样机的几何参数

注:s为并联模块行程;qmin和qmax为支链的最小和最大腿长;θS、θU和θR分别表示球铰、虎克铰和转动副的极限转角;D表示弧形导轨的直径;L表示串联模块沿Y轴方向的直线行程。

经计算,上述并联模块和混联制造系统的工作空间V和W分别如图8a和8b所示。

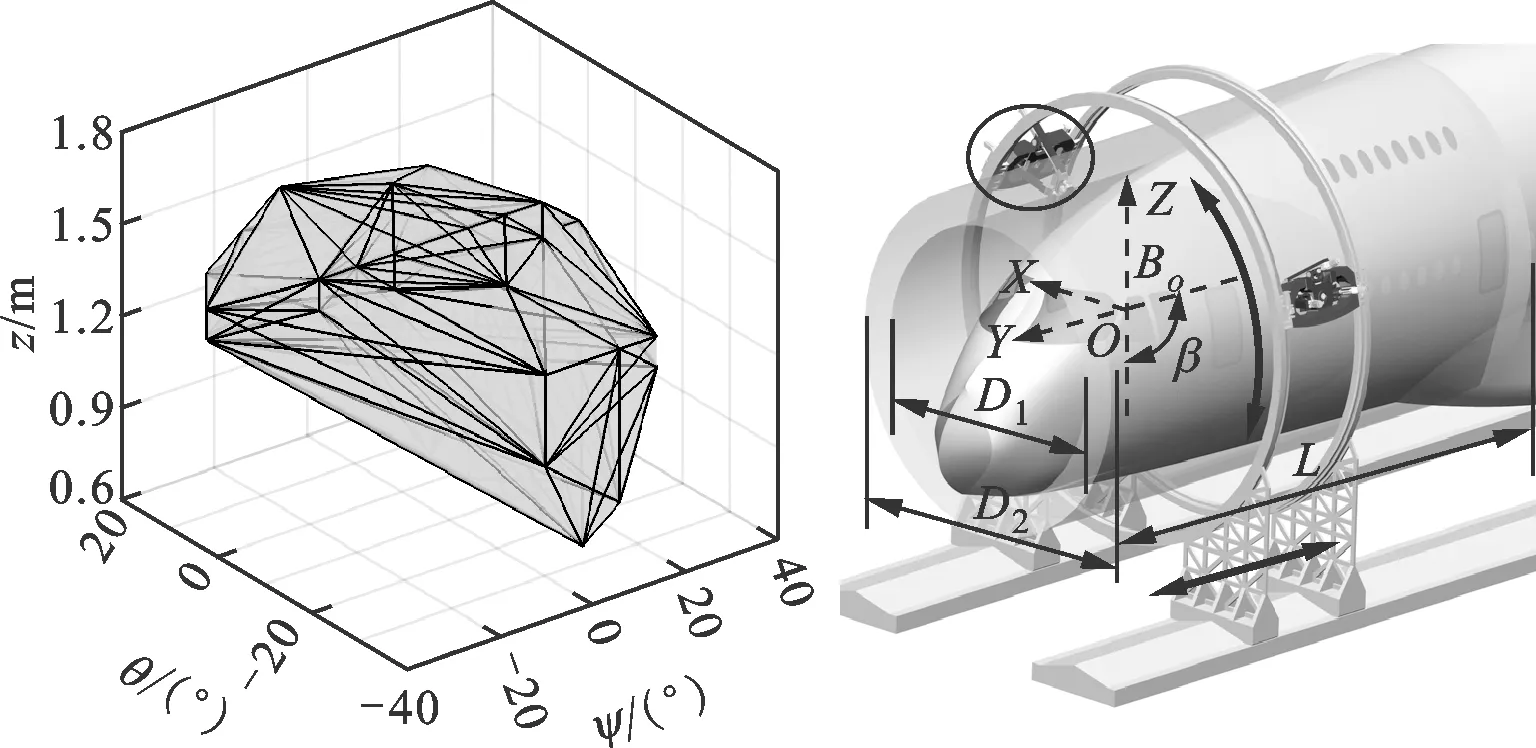
(a)并联模块工作空间V (b)混联制造系统工作空间W图8 工作空间示意图

由图8可知,并联模块动平台的转角范围为θ∈[-40°,20°]和ψ∈[-38°,38°],转角工作空间体积为0.300 m·rad2;混联系统的可达工作空间W呈圆筒形,其内、外直径D1和D2分别为8.00 m和9.66 m,工作空间体积为470.62 m3。

3 弹性静力学建模

根据混联柔性制造系统的结构特点,在进行弹性静力学分析时做如下设定:

(1)因弧形导轨、动平台和静平台的刚度远高于其他构件,故忽略该部分的变形而将其视为刚体;

(2)计入各铰链的柔性,将其简化为具有等效刚度且位于铰链几何中心的集中弹簧;

(3)计入各支链体的柔性,并根据支链结构特点将其等效为规则截面的空间梁;

(4)忽略各运动副处的摩擦、阻尼和间隙等非线性因素以及机构运行时的刚体惯性力。

3.1 受力分析

基于前述建模假设,为便于表述,可在坐标系Bo-xyz下分析机械结构和位置变化更为复杂的并联模块,并将运动支链简化为受2组具有等效刚度的集中弹簧约束的等效空间梁。采用2节点12自由度的空间梁单元对图9a所示的支链体划分网格,并保证Ai、Bi和Ci为其上3个节点。经整理,可得坐标系Ai-xiyizi下支链i的静力平衡方程为

kiξi=wi(i=1,2,3)

(23)

式中:ki表示支链坐标系中支链体的刚度矩阵;ξi和wi分别表示支链坐标系中节点广义坐标列阵和外载荷列阵。

在坐标系Bo-xyz下对支链体和动平台进行受力分析,受力状况分别如图9a和9b所示。

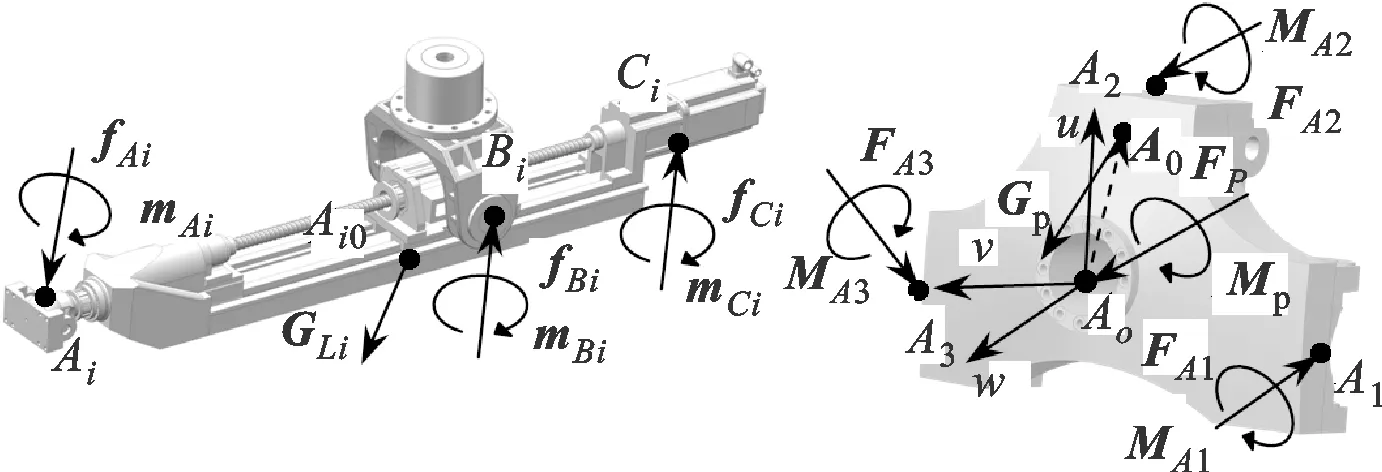
(a)支链体(b)动平台图9 支链体和动平台的受力简图

图9a中,fAi/mAi、fBi/mBi和fCi/mCi(i=1,2,3)分别为支链坐标系Ai-xiyizi下作用于Ai、Bi和Ci点的约束反力/反力矩;GLi为坐标系Bo-xyz下的支链重力矢量,表达式为

GLi=mLig(β)

(24)

式中:mLi表示支链i的质量;g(β)为重力加速度在坐标系Bo-xyz下的表达,可由以下坐标变换获得

g(β)=BTOg=rot(Y,β)g

(25)

其中,g为混联系统坐标系O-XYZ下的标准重力加速度矢量(大小取9.8 m/s2),方向为沿Z轴负方向。

图9b中,Fp和Mp分别表示参考系Bo-xyz下作用于动平台的外力和力矩;FAi和MAi为B-xyz下动平台与支链连接处的关节约束反力和反力矩,且

FAi=BTAifAi;MAi=BTAimAi

(26)

Gp为Bo-xyz下动平台重力矢量,表达式为

Gp=mpg(β)

(27)

式中:mp表示动平台的质量。

动平台和支链i的重力在坐标系Bo-xyz下的等效力矩可表示为

τBp=a×Gp;τBi=li×GLi

(i=1,2,3)

(28)

类似地,动平台和支链i的重力在动平台坐标原点Ao处的等效力矩可表示为

τAp=-r×Gp;τAi=-r×GLi

(i=1,2,3)

(29)

由牛顿第二定律可得动平台静力平衡方程

(30)

式中:rAi为参考系Bo-xyz下由Ao点指向Ai点的方向矢量。

3.2 弹性变形分析

图10所示为支链与动、静平台间的位移关系。

图10 支链体与动、静平台之间的位移关系

图10中:kA1i、kA2i分别为Ai点处运动铰链的等效线刚度和等效角刚度,AiM和AiL分别表示耦合界面上动平台和支链i上的节点,Ai和δAi分别表示支链坐标系Ai-xiyizi下AiM的线位移和角位移;εAi和ξAi分别表示支链坐标系Ai-xiyizi下AiL的线位移和角位移;kB1i、kB2i分别为Bi点处运动铰链的等效线刚度和等效角刚度,BiL和BiB分别表示耦合界面上支链和静平台上的节点,δBi和ρBi分别是支链坐标系Ai-xiyizi下BiL的线位移和角位移。

计入支链体与动、静平台之间的变形协调关系,可得Ai点处铰链的弹性线位移和角位移为

ΔAi=εAi-

(i=1,2,3)

(31a)

(i=1,2,3)

(31b)

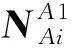
Ti=diag[BTAi,BTAi,…,BTAi,BTAi]

(i=1,2,3)

(32)

同理,可得Bi点处铰链的弹性线位移和角位移

(33)

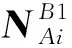
3.3 弹性静力学模型

前述支链坐标系下的静力平衡方程式(23)在参考系Bo-xyz下可表示为

KiUi=Wi(i=1,2,3)

(34)

式中:Ki、Ui和Wi分别表示坐标系Bo-xyz中支链的刚度矩阵、位移列阵(同式(31)中的Ui)和外载列阵,并可表示为

(35)

将式(31)～(33)代入式(30)和(34),整理可得系统的弹性静力学方程

KU=W

(36)

式中:K、U和W分别为坐标系Bo-xyz下系统的刚度矩阵、位移列阵和外载列阵。其中位移列阵U

(37)

大型航空结构件的高速加工与装配过程中,作用于并联模块动平台上的外载荷一般远小于自重,所以可认为并联模块自重是造成混联系统发生弹性变形的主要因素[19-20],此时,系统外载列阵W

(38)

当仅考虑混联系统自重时,执行末端动平台的等效外力和外力矩Fp和Mp分别为

(39)

(40)

此时,系统位移列阵U可进一步写成

U=K-1W

(41)

将式(39)和(40)的等效外力和外力矩带入式(41),通过位移列阵U即可提取动平台弹性位移Up,其沿坐标轴方向的位移分量即为混联系统执行末端动平台在相应方向的弹性位移量。

4 弹性静力学分析

4.1 系统参数

基于上述模型,对混联柔性制造系统进行弹性静力学分析。表2所示为该系统并联模块的部件质量参数和支链坐标系下各关节的刚度系数。

表2 部件质量与各关节的刚度系数

表2中:kAij(i=l,s,c;j=x,y,z)为Ai点处铰链的长轴(l)、短轴(s)和交叉轴(c)沿各相关方向的等效线刚度系数;kAv和kAw表示Ai点处铰链的等效角刚度系数;kBj(j=x,y,z,v,w)为Bi点处铰链沿各相关方向的等效线刚度和角刚度系数。表中,动、静平台质量由虚拟样机模型直接获取;各刚度参数值由有限元仿真确定。

4.2 典型位姿下动平台的弹性位移

取β=45°、90°和135°(z=1 350 mm,θ=0°,ψ=0°)来分析混联柔性系统在3个典型位姿下的静力学特性。由式(41),可求得在系统重力作用下动平台的弹性位移,结果如表3所示。表中,εpj和ξpj(j=x,y,z)分别表示动平台沿x、y和z轴的线位移和绕x、y和z轴的角位移。

表3 动平台弹性位移

由表3可知,该混联系统的静力学性能受并联模块位姿角β的影响。当仅受自重时,混联系统末端的动平台产生沿x、z轴和绕y轴的弹性位移。其中,沿x轴方向的弹性变形量远大于沿z轴方向的弹性变形量,表明该混联系统沿x轴方向的刚度较弱,在设计阶段应予以充分重视。另外,自重使得末端的动平台产生绕y轴方向的扭转变形,表明动平台末端执行绕y轴转动时应予以适当运动补偿,以部分抵消扭转变形带来的误差。

进一步分析发现,在上述3个典型位姿下,系统动平台沿y方向的线位移εpy和绕x、z轴的角位移ξpx、ξpz均为0,表明这3个方向的弹性变形不受自重影响。这是因为当系统处于上述3个典型位姿时,动平台的摆角为θ=0°,ψ=0°,此时支链1和支链3关于x-z平面对称,导致系统自身重力仅作用于x-z平面,故系统不会产生平面外的弹性变形。

为验证上述弹性静力学模型的计算精度,在ANSYS Workbench(Vision:15.0.0)中应用静力学结构分析模块建立3种典型位姿下系统的有限元模型,施加相应的重力加速度g(β),经分析得到相应方向的弹性变形。篇幅所限,仅给出并联模块沿x轴的位移云图,如图11所示。

(a)β=45°(b)β=90°(c)β=135°图11 并联模块沿x轴方向的位移云图

由图11可知,并联机构模块动、静平台自身的变形近似为0,支链体与铰链均产生一定变形,与前文将动、静平台视为刚体而将支链体和铰链视为柔性体的建模假设一致。此外,同时考虑串联导轨自重(加载标准重力加速度9.8 m/s2)和其承载的并联模块重力(加载并联模块总质量1 664 kg),并加载等效合力于典型位置(例如β=166°处),经计算分析,可得圆弧导轨沿主要弹性变形方向的最大弹性变形量为1.35 mm,仅相当于导轨直径的0.012%,这与前文将圆弧导轨视为刚体结构的建模假设一致。

进一步分析可得并联模块动平台沿x方向的弹性变形,如表4所示。

将有限元模型的仿真结果与前述弹性静力学分析结果对比,发现2种模型的计算结果吻合较好,由二者获得的动平台沿x轴方向的弹性位移的计算误差不超过6%,表明前文所建的弹性静力学模型具有较高的计算精度,可用于混联柔性制造系统全局静力学性能的预估。

表4 并联模块动平台沿x方向的弹性变形

4.3 系统全局静力学性能评估

4.2节指出,混联柔性制造系统的静力学性能与并联模块安装的位姿角有关。为评估系统工作全域内的静力学性能,选取动平台弹性位移在其工作空间V内的均值为指标,来考察系统性能与位姿角β的映射关系。

(j=x,y,z)

(42)

由上式可知,平均位移指标表征的是系统在外载荷作用下于相应方向产生的弹性位移,与相应方向的真实位移具有相同的量纲。显然,平均位移指标值愈趋近于0,系统的刚度愈大,有望实现的加工性能愈好,反之愈差。因此,所述平均位移指标可定量地反映系统弹性位移随并联模块安装位姿角的变化关系,指明可能的优秀加工运行区间,相应计算结果如图12所示。

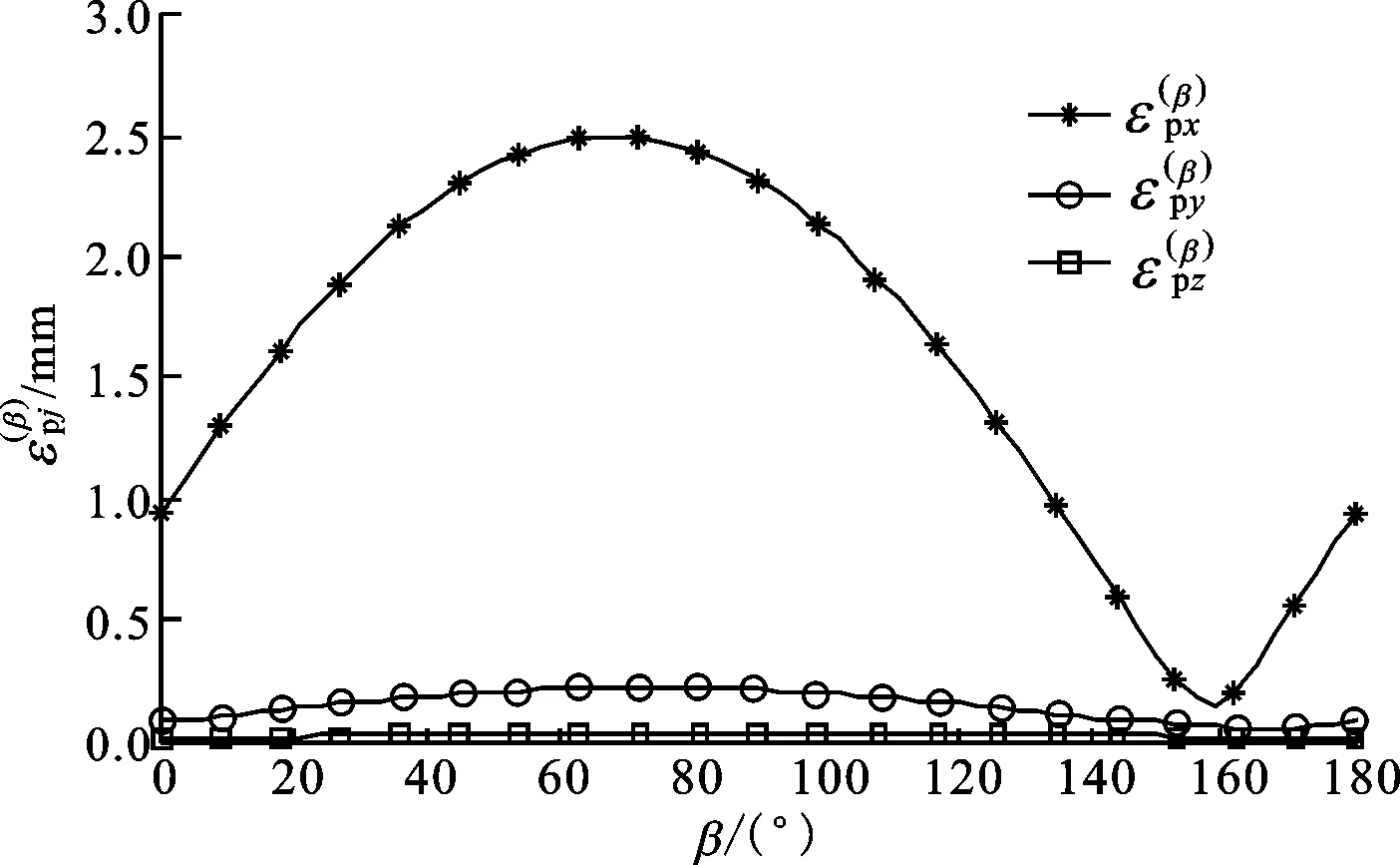
(a)平均线位移指标

(b)平均角位移指标图12 动平台平均位移指标随β的变化

5 结 论

(1)设计了一种用于大型航空结构件加工与装配的5自由度混联柔性制造系统。该柔性制造系统兼具弧形导轨工作空间大和并联模块刚度高的优点,有望为大型航空结构件的柔性制造提供一种技术解决方案。

(2)运用虚拟样机技术完成了5轴混联柔性制造系统的概念设计,并通过运动学分析揭示了该柔性制造系统的工作空间特性,其可达空间呈圆筒状分布,工作空间体积达470.62 m3。

(3)借助子结构综合法建立了该柔性制造系统的弹性静力学模型,揭示了混联系统在典型位姿下的静力学特性,并对其进行了数值仿真验证。分析表明,在进行该混联柔性制造系统设计时,需要着重提高其沿x轴方向的抗弯能力和绕y轴方向的抗扭能力。

(4)提出以并联模块工作空间内的平均位移作为指标来度量系统工作全域内的静力学性能。性能指标分析表明,当并联模块的位姿角位于63°～69°时,系统受机构自重产生的弹性变形最大,应予以特别重视。