等级年龄结构种群模型平衡态研究
夏洪涛,刘 炎
(中国计量大学 理学院,浙江 杭州 310018)
用动力学方法来研究物种的发展规律,最早始于十八世纪。1798年,英国神父T.R.Malthus在他著作里第一次提出Malthus人口模型,得出人口会以指数无穷增长。在现代的种群动力学理论来看这个模型有很多缺陷,因为这个模型考虑的因素比较单一,但是在一定范围内,Malthus模型可以很好的预测种群增长规律,比如18世纪的澳大利亚的由于缺少天敌,食物充足发生的兔灾,可以用Malthus模型得到比较正确的预测结果。
Verhulst(1838-1845)改进了Malthus模型提出了logistic方程,这个模型考虑了环境的最大生物容纳量,种群的增长速率和环境的最大容纳量有关。logistic模型的前期基本符合模型的Malthus模型增长规律,但是到了后期,由于环境中资源是有限的以及自身的密度制约,种群的自然增长率自然放缓直至种群数量进入平衡状态,这样一个种群必然存在最大增长率。由于这个原因,现代,这个模型在研究农业、畜牧业、渔业最大可持续产量有着广泛应用。虽然logistic模型解决了Malthus模型的一些缺陷,但是这两个模型均没有考虑种群中个体对种群的影响。
在1926年,内科医生McKendrick首次将年龄结构引进单种群动力学模型,McKendrick模型是将关于种群总数(或密度)的函数用时间和年龄两个变量来刻画。结构化的模型相对于上述两个模型,可以将种群中的个体与种群结合起来,可以考虑很多上述两个模型不能很好解释的问题,比如在考虑人口增长问题时当人口中男女比例失衡、人口老龄化严重的问题时,采用年龄结构模型可以更好的预测人口数量发展趋势。基于McKendrick研究的年龄结构模型在过去30年中得到了广泛的研究[1?8]。
传统的年龄结构种群模型研究工作对于出生率和死亡率主要取决于年龄和时间,但是在许多生物种群中可以观察到年龄高的个体对同一物种的生存率的影响在自然界中广泛存在[9],虽然分层结构模型可以很好地模拟大多数生物物种,但是由于生物的出生率和死亡率是高阶非线性的,处理分层结构模型是具有挑战性的工作。Cushing研究了一个等级年龄结构的生物种群的长期行为[10]。Henson和Cushing引入了层次化的年龄结构模型研究竞争对人口演变的影响[11]。Gurney和Nisbet建立了捕食者捕食模型,其中捕食者是一个等级年龄结构。他们分析了模型通过随机方法得出结论,等级差异更有利于生物群体的稳定性[12]。Calsina和Saldan通过建立具有分布式出生状态和分层结构的PDE模型,提出了等级年龄结构模型的一类解决方案[13]。最近,何泽荣研究了等级年龄结构模型的解的存在唯一性并进行了近似解的收敛性分析解决方法[14]。本文主要研究等级年龄结构模型的解存在性和唯一性,以及平衡态的存在性、稳定性。本文结构如下:第1部分给出了等级年龄结构模型的基本假设以及解的存在唯一性,第2部分给出了平衡态的存在性以及稳定性的条件,最后对本文的工作做了简要总结。
1 等级非线性结构
如果出生模和死亡模函数不仅与个体年龄和时间有关,而且与同一种群内其他个体有关系,这样的模型可以描述为
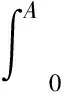
(1)

1)死亡率μ(a,E(p)(a,t))≥0且μ在(0,A)×(0,T]上有界。此外,μE存在且満足lipschitz条件和0≤μE<+∞;

3)p0(a)非负有界。
对于模型(1)的解,如果p(a,t)∈L∞((0,A)×(0,T])且于任意t∈(0,T]以及任意ξ∈C1(Qt)有

(2)
则称p(a,t)为模型(1)的形式解。
为了研究解的性质,先定义模型(1)的上下解。

3)于任意t∈(0,T]以及非负ξ∈C1(Qt),有以下成立

(3)
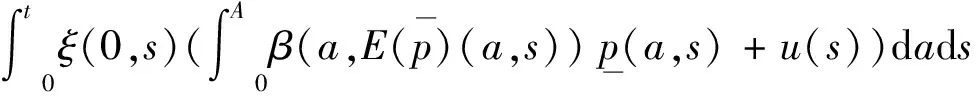
(4)
运用上述定义,我们可以建立以下比较原则。

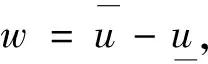
(5)
由(3)(4)式及微分中值定理可得
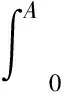
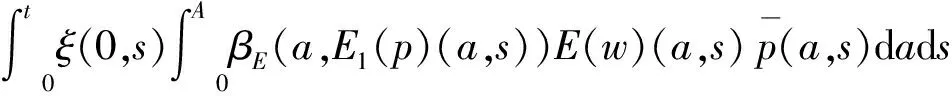
(6)




(7)
考虑如下问题:
ζs+ζa=0, 0 (8) ζτ+ζa=0, 0 ζ(a,τ)=X(a), 0 (9) 由(9)式可知在Qt上恒有0≤ζ(a,t)≤1,此外注意到 (10) 其中w+为w的正则函数。 将上述结果代入(7)式 综上所述,可得 (11) 在a∈(0,A)上,令函数X(a)如下: 利用(11)式可得 再运用Gronwall不等式,对任意t∈(0,T]都有 定理1.1证明完毕。 接下来证明解的唯一性。 定理1.2若假设1)~3)成立,则模型(1)至多有一个解。 证明设p1,p2分别是模型(1)的两个解,令p=p1-p2,由(2)式及微分中值定理可得 (12) 这里ηi介于E(p1)(a,s)和E(p2)(a,s)之间(i=1,2),选取ξ∈C1(Qt)满足 ξs+ξa=0, 0 ξ(A,s)=0, 0 (13) ξ(a,t)=Y(a), 0 可以得到 再运用Gronwall不等式,对任意t都有 定理1.2得证。 考虑如下系统模型的平衡态: (14) 这里的变量以及参数函数的生态意义与系统模型(1)相同,基本假设也与第一节相同。 如果系统达到平衡,则不需要人工干预,即u(t)=0,则模型(14)的平衡解p*(a)满足如下方程: (15) 对此方程组进行求解,得到 (16) (17) 由式(17)可以看出模型存在零平衡态,若模型(14)存在正平衡态,则p*(0)非零,则由(17)第一式可以得到 令E*=E(p*)(a),设 R(E*)定义为基本再生数,接下来证明正平衡态的存在性。 dτ→+∞(E*→+∞),则模型(14)有唯一正平衡态,它形如(16)式。 证明对于一个固定的p*(0),定义如下关于E*的连续函数 容易得到 G(0)<0,G(+∞)>0。 接下来研究平衡态的稳定性,定义扰动u(a,t)=p(a,t)-p*(a),这里p*(a)为平衡点,将此式代入(14)并利用(15)可以得到 ua(a,t)+ut(a,t)=-μ(a,E(p)(a,t))p(a,t)+ μ(a,E(p*)(a))p*(a)。 (18) 容易得到 E(p)(a,t)=E(u)(a,t)+E*。 将(18)线性化去掉u的非线性项,得 ua(a,t)+ut(a,t)=-μ(a,E*)u(a,t)-μE(a,E*)p*(a)E(u)(a,t)。 同样对初始状态进行线性化 u(0,t)=p(0,t)-p*(0)= 这样可以得到模型(14)-(15)在p*(a)处的线性化,如下: ua(a,t)+ut(a,t)=-μ(a,E*)u(a,t)- μE(a,E*)p*(a)E(u)(a,t); (19) (20) 对这个方程求解得到 U(a)=[U(0)- (21) 其中 将U(a)代入(20)第二个式子得 (22) 其中 根据上述条件可以得到方程组 (23) 由上述方程组易得模型(14)-(15)有非平凡解充要条件为方程组(23)的系数行列式为0。 定理2.2方程组(19)存在形如u(a,t)=eλtU(a)的形式解的充要条件是λ是如下特征方程 的根。 证明由线性系统的理论易证。 定理2.3对于线性系统模型(1),若特征方程F(λ)=0存在具有正实部的根,则系统的平衡态p*(a)不稳定;若特征方程所有的根都有负实部,那么平衡态p*(a)是渐近稳定的。 下面考虑线性系统的平凡解,此时p*(a)=0,则 =A21(λ)-1 =F0(λ)。 这样可以得到以下平凡平衡态的判别依据。 推论2.1当特征方程F0(λ)存在具有正实部的根时,系统的零平衡解不稳定,当特征方程所有的根都有负实部,此时零平衡解是渐近稳定的; 对于非平凡平衡态,我们只研究正平衡态,为了更为容易获得具体的判别条件,考虑μ与E*无关的情形。 推论2.2设μ与E*无关,则当K>0时,正平衡态不稳定,则当K<0时,正平衡态渐近稳定,其中 证明因为μ与E*无关,此时 其中 得到 令G(λ)=F(λ)+1,则F(λ)=0等价于G(λ)=1。 接下来考虑K<0的情形,假设G(λ)=1存在一个根为λ=x+yi(x≥0),可以得到 1=Re(G(λ))= K+1<1。 推出矛盾,所以G(λ)=1不存在正实部的根,这样可得当K<0时,特征方程G(λ)=1只有负实部的根,则正平衡态渐近稳定,推论2.2证明完毕。 本文主要研究等级年龄结构模型的两个方面:一是等级年龄模型解的存在唯一性,二是平衡态的存在稳定性。采用微分方程解的比较原理、Gronwall不等式等方法获得了等级年龄结构模型解的存在唯一性。在研究平衡态问题时,首先建立平衡态的系统模型并利用函数介值性定理推得平衡态的充要条件,最后借助研究特征方程解的方法来研究平衡态的稳定性并给出稳定的判别条件。对于可以达到平衡态的生物种群,可以利用平衡态的稳定性判别条件,可以根据实际需要来调节生物个体的参数来控制生物种群数量或种群密度;比如对有害的生物种群可以通过改变个体参数使零解渐近稳定,使非平凡解不稳定,以此达到减少危害的目的;对于有益种群可以通过调节个体参数使零解不稳定,使非平凡解稳定,以此达到有益种群可持续生存的目的。
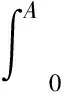


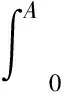




2 平衡态稳定性研究
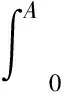

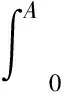
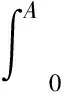
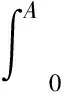
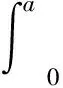


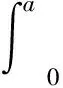








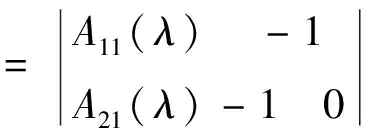



3 结 语

