有限域上稀疏多元多项式插值算法*

唐 敏，邓国强

桂林电子科技大学 数学与计算科学学院 广西密码学与信息安全重点实验室，广西 桂林 541004

1 引言

插值是函数逼近的重要方法，利用它可通过函数在有限个点处的取值情况，估算出函数在其他点处的近似值。在信号处理[1]、不确定性量化[2-4]、压缩感知[5]、图像处理[6-7]等领域需要有效地利用较少的函数值恢复一个函数，而这个函数往往具有稀疏的表示形式，稀疏插值能有效地处理此类问题。稀疏多元多项式插值是一种降低计算机代数算法时间复杂度的有效方法，是稀疏有理函数插值[8]及稀疏隐函数插值[9]的基本步骤，应用在结式计算[9]、多元多项式GCD计算[10-12]、方程求根、数值微分、数值积分、曲面的外形设计和有限元法及上述提及的诸多应用领域。因此提高稀疏多元多项式插值的效率十分有意义。

对于多元多项式，稠密插值所需的插值点个数为(d+1)n，其中d是变元的次数，n是变元的个数。研究工作表明，多元多项式插值算法的计算复杂度与变元个数可以不呈指数关系，而是与目标多项式的稀疏性相关，即是关于n、d、t和lbp的多项式函数，其中t是目标多项式的项数，素数p是有限域的特征。

1979年Zippel提出了第一个具有多项式时间复杂度的稀疏多元多项式插值算法[12]。该算法基于这样的假设：如果在一个随机的赋值点处多项式的取值为零，那么它就是一个零多项式。由于这个结论的成立是高概率的，因此Zippel算法是一个概率性的方法。在执行上，Zippel算法顺序地对每个变元逐一插值，不能并行化，插值点个数为ndt，时间复杂度为O(ndt3)。1990年，Zippel改进了他的方法[13]，使用了形如的插值点，原算法中需要计算的一般线性系统变成了转置的Vandermonde系统，求解时间从O(t3)降到O(t2)。由于Zippel算法是一种较好的具有多项式时间复杂度的方法，大部分计算机代数系统都内置了基于Zippel算法的多元GCD计算的实现，比如Macsyma、Magma和Mathematica。

1988年，Ben-Or和Tiwari提出了一个确定性的算法[14]，可以对以整数、有理数、实数或复数为系数的多元多项式进行稀疏插值。给定项数为t的多项式f的项数界T≥t，算法需要2t个插值点，即前n个素数 的 幂 次，0≤i≤2t-1。该方法与Zippel算法不同，不是逐个变元的插值，而是一次性地对f的各个单项式进行插值，而且可以并行化。主要的不足是插值点的存储空间为tlbn位，当多项式规模较大时，由于中间表达式膨胀而导致计算速度非常慢。

2000年，Kaltofen等设计了一个Zippel和Tiwari方法相结合的混合算法，称之为“racing算法”[15-16]。为了减少插值点个数，在Zippel算法中插值下一个变元的时候，同时执行Newton插值和单变元的Ben-Or/Tiwari插值，取其快者。

2010年，Javadi和Monagan提出了一个有限域上的稀疏多元多项式插值算法[17]，它也是一个概率算法。该方法是Ben-Or/Tiwari算法的一个改进，使用O(t)个插值点独立完成每个变元的插值，共需O(nt)个插值点，并且可以并行化。为了准确计算每个变元在各个单项式中的准确次数，使用了二部图完美匹配进行测试和验证。该算法和Zippel算法及Kaltofen的racing算法进行了比较，在运行时间和插值点个数等方面具有一定的优势。

2011年，Cuyt和Lee给出了稀疏有理函数插值算法[8]，其中涉及到单变元有理函数插值和基于Zippel算法及Tiwari算法的稀疏多元多项式插值。2016年，基于Cuyt的稀疏有理函数插值算法，Tang给出了稀疏隐函数插值算法[9]。在稀疏有理函数插值和隐函数插值算法中，稀疏多元多项式插值作为基本的子函数，对整个算法的效率起到关键作用。

本文提出了一个有限域上的稀疏多元多项式插值算法，它是Javadi/Monagan算法的改进，改进方案主要有两点：一是消除了必须给定项数界T的限制，通过计算预先设计好的特定矩阵的行列式，得到f的准确项数；二是消除了必须给定次数界D的限制，通过构造辅助函数，利用概率法结合提前终止技术的Cauchy插值法，计算出f的准确次数，解决了Javadi和Monagan论文中提到的次数界D过高而导致高计算复杂度的问题。更进一步，改进算法无需给定T和D，对于实际问题在利用插值恢复或近似时更具实用性。

本文后续组织结构如下：第2章介绍了Javadi/Monagan算法的基本思想；第3章给出了改进的Javadi/Monagan算法；第4章分析了改进算法的时间复杂度；第5章中设计了三组数值实验，对改进算法和Javadi/Monagan算法进行了比较，给出了实验结果；第6章给出了一个应用实例。

2 Javadi/Monagan算法

本章给出稀疏多元多项式插值问题的形式化定义及Javadi/Monagan算法的思想。

2.1 稀疏多元多项式插值问题的形式化描述

令p是一个素数，f∈Zp[x1，x2，…，xn]是一个用黑盒表示的多元多项式：

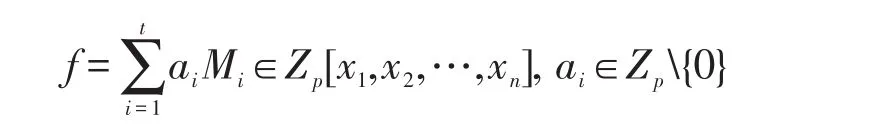
稀疏多元多项式插值的目标是用尽可能少的插值点及较低的多项式时间复杂度算法还原多项式f。

2.2 Javadi/Monagan算法的思想

Javadi/Monagan算法可分成两个步骤，首先确定各个单项式，然后确定系数。在第一个步骤中，逐一计算每个变元在各个单项式中的次数。第二个步骤需要求解一个Vandermonde线性代数系统。同时要求给定f的项数界T≥t及次数界D≥degf。

（1）确定单项式Mi，i=1，2，…，t。

③使用Berlekamp/Massey算法[18]生成n+1个关于z的单变元多项式，使得，其中i=0，1，…，2t-1,j=0，1，…，n。

④确定变元xk，k=1，2，…，n在f中的单项式Mi，i=1，2，…，t中的次数eij。详见2.3节。

⑤由④可确定eij，i=1，2，…，t，j=1，2，…，n，则单项式

（2）计算系数。

通过求解线性方程组计算系数ai，i=1，2，…，t。令r1，r2，…，rt是Λ1(z)的根，且ri=Mi(α1，α2，…，αn)，回顾是输入为时黑盒的输出，因此有：

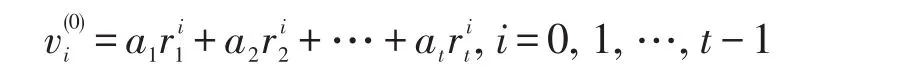
此为Vandermonde系统，有唯一解。

2.3 确定变元xk的次数

令R1={r1，r2，…，rt}和分别是Λ1和Λk+1的全部根构成的集合。令Dj包含单项式Mj中xk的所有可能的次数，即：

二部图Gk定义如下：U和V是二部图Gk中顶点个数为t的互补顶点子集，U和V中的结点表示R1和Rk中的元素，即ui∈U，vj∈V，分别用ri和标记，ui和vj之间有一条权值为dij的边当且仅当

引理1[17]变元xk在所有单项式中的次数可唯一确定当且仅当二部图Gk有唯一的完美匹配。

以下给出为计算xk的次数，构造的二部图Gk没有唯一的完美匹配时的解决方案。

随机选择不同于α1，α2，…，αn+1的元素令，使用 Berlekamp/Massey算法，以v′i=f(β′i)，0≤i≤ 2t-1为输入，生成多项式Λ′k+1(z)。令是Λ′k+1(z)的根构成的集合，G′k是通过Λ1(z)和Λ′k+1(z)构造的二部图。

定义1[17]二部图G′k与Gk的交集定义如下：与G′k具有相同的结点，ri和之间有权值为dij的边当且仅当在二部图Gk中，ri连接且在二部图G′k中，ri连接权值均为dij。

引理2[17]令eij=degxj(Mi)，在二部图中，结点ri和之间有边相连，且权值为eij。

定理1[17]令的交集有唯一的完美匹配。

引理1、引理2和定理1的证明参考文献[17]。由定理1，如果Gk没有唯一的完美匹配，可通过增加2t个插值点，构造二部图来确定变元xk在单项式Mj(1≤j≤t)中的次数。

3 改进的Javadi/Monagan算法

本章给出对Javadi/Monagan算法进行改进的两个主要策略。3.1节和3.2节分别描述了如何只利用黑盒的输入输出（即有限个插值点），计算多项式f的准确项数t和准确次数d，从而消除了原算法必须预先给定这两个指标的上界的限制，同时提高了实用性及降低了计算时间复杂度(分析过程见第4章)。

3.1 f的项数t的计算

除了Javadi/Monagan算法，许多插值算法都要求给定目标多项式f的项数界T，本文给出一个准确计算多项式f的项数t的方法。该方法由定理2保证。

定理2[14]令V是元素为(V)ij=vi+j-2的矩阵。Vl是由V的前l行前l列组成的方阵。如果t是多项式f的准确项数，即f中非零单项式的个数，那么：

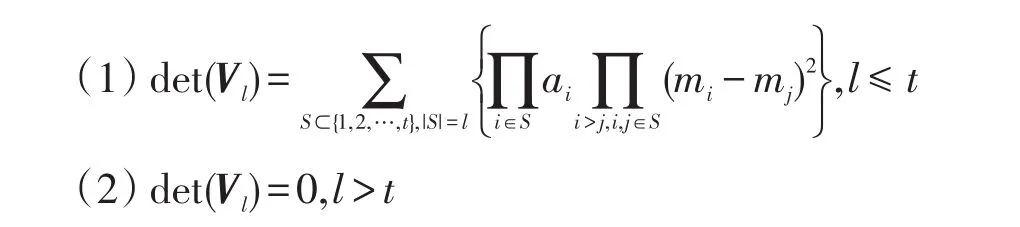
根据定理2，通过下述过程可计算f的准确项数：

例如：黑盒多元多项式f定义为：令p=1 009，随机生成中的3个整数，比如α1=66，α2=12，α3=3。

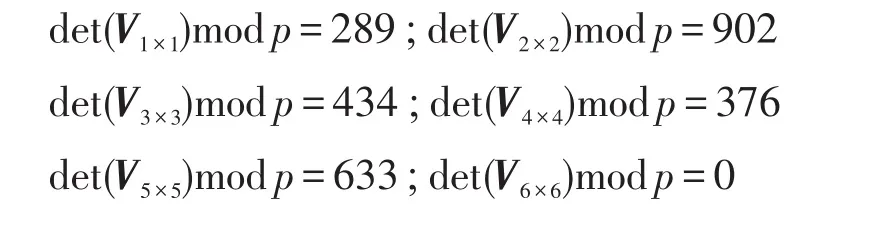
因此多项式f的准确项数为5。

3.2 f的次数d的计算

在2.3节构造二部图的过程中，计算单项式Mj中xk的所有可能的次数Dj时，需要检测的次数为D+1。因此Javadi/Monagan算法在给定的次数界过高时，会导致高计算复杂度。本节利用单变元有理函数插值计算f的准确次数d，使得在确定每个变元的次数时，时间复杂度达到最低。方法描述如下：

（1）构造辅助有理函数H。

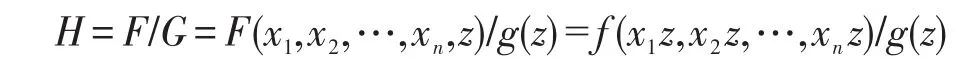
通过在f中引入齐次变元z，构造f为分子，g为分母的辅助有理函数H。其中f(x1，x2，…，xn)为黑盒多项式，g为随机生成的关于变元z的一次多项式。若视F为关于变元z的单变元多项式，则系数为关于x1，x2，…，xn的多元多项式，注意到系数多项式与z是齐次的。

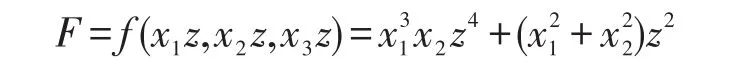
易证f的全次数与F中z的最高次相同。

（2）对H进行单变元有理函数插值。

任取n元组 (α1，α2，…，αn)，对H进行关于变元z的单变元有理函数插值，可得到：

（3）H(α1，α2，…，αn，z)的分子f(α1z，α2z，…，αnz)关于z的最高次即为黑盒多项式f的全次数。

假设f(α1z，α2z，…，αnz)和g(z)有非平凡的公因子，即g(z)|f(α1z，α2z，…，αnz)，也就是说，g(z)的根也是f(α1z，α2z，…，αnz)的根。因为g(z)是随机生成的，而f(α1z，α2z，…，αnz)的根是有穷的，所以f(α1z，α2z，…，αnz)和g(z)高概率互素，从而f(α1z，α2z，…，αnz)关于z的次数即为黑盒多项式f的全次数。

令 (α1，α2)=(1，1)，g=5z+3 ，则：

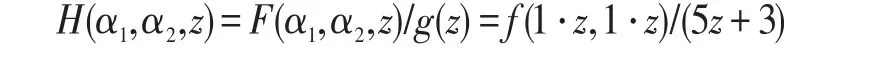
利用单变元有理函数插值可得到H(1，1，z)=(z4+2z2)/(5z+3)，则f的准确次数为H的分子中z的最高次，即为4。

接下来给出单变元有理函数插值的实现过程。对于单变元有理函数f/g∈Κ(Z)，应用文献[19]提出的概率方法，并结合提前终止技术的Cauchy插值来恢复f/g。来源于文献[19-20]的引理给出了单变元有理函数插值的理论基础。

引理3[20]令Κ是任意域，F(Z)，G(Z)，H(Z)∈Κ(Z)且 gcd(F，G)=1。令是非负整数，且1。令ik，f/g∈Κ(Z)不必是Κ中互不相同的元素，满足：

对于l≥ 2 ，令hl(Z)，ql(Z)∈Κ(Z)分别是Euclidean多项式余项序列中的第l次余项和商。

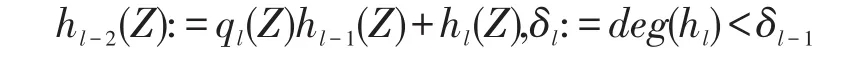
对于l≥ 2 ，令wl(Z)，gl(Z)∈Κ(Z)是扩展Euclidean方法中的乘子wlh0+glh1=hl，即：

那么存在下标j≥ 1满足，并且对下标j有：

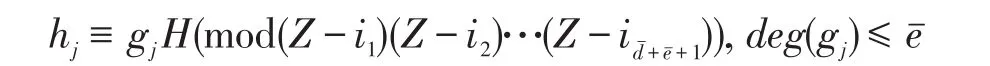
根据引理3，如果给定单变元有理函数的次数上界，使用扩展Euclidean算法可计算有理函数的分子和分母。在文献[19]中，提出了基于引理3的单变元有理函数插值算法。为确定准确的f/g的次数，可对k从1迭代到d+e+1，其中d、e分别是f和g的次数。

基于概率法和提前终止技术的Cauchy插值法恢复单变元有理函数，算法描述如下：

算法1单变元有理函数插值算法

其 中 Interpolate(i1，i2，…，ik;H(i1)，H(i2)，…，H(ik)) 表示给定k个点 (i1，H(i1))，(i2，H(i2))，…，(ik，H(ik))的自变量和函数值，利用Newton插值或Lagrange插值得到次数为k-1的单变元多项式；Rem表示余式，Quo表示商。

黑盒多项式f的次数即为deg(h1)。

3.3 改进算法

本节给出改进的Javadi/Monagan算法的伪代码。

算法2改进的Javadi/Monagan算法(有限域上稀疏多元多项式插值算法)

以下给出改进的稀疏多元多项式插值算法的一个实例。黑盒多元多项式f定义为：

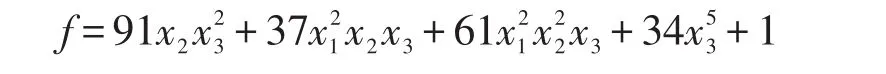
令p=101，变元个数n=3。重构f的过程如下：

（2）计算出多项式f的准确项数t=5。

（4）计算Λk(z)，k=1，2，…，4:

令vi=B(βi)，i=0，1，…，2t-1，当k＞1时，用替换使用Berlekamp/Massey算法生成由序列v0，v1，…，v2t-1得到的Λk∈Zp(z)：

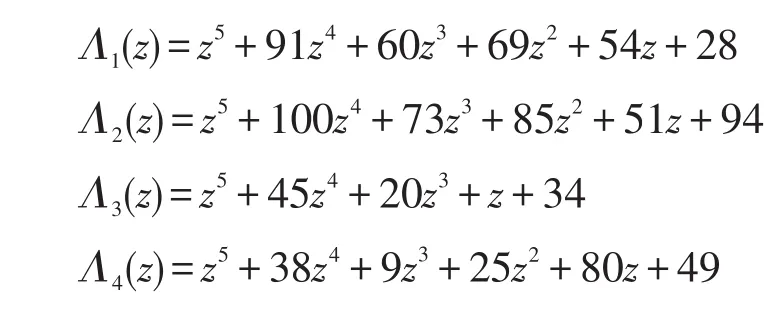
（5）计算出多项式f的次数d=5。

（6）确定degxk(Mi),1≤i≤t,k=1，2，…，n。

以第1个变元x1为例，计算Λ1的根：

计算Λ2的根：

测试rj×(αn+1/α1)i，0≤i≤d，j=1，2，…，t,得到：

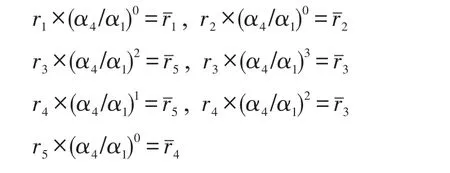
构造二部图G1，如图1所示。

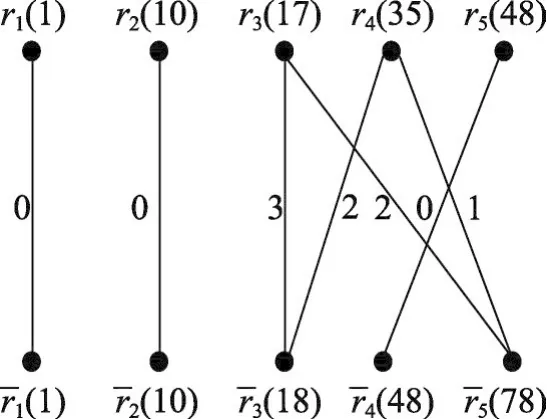
Fig.1 Bipartite graphG1图1 二部图G1

因为二部图G1没有唯一的完美匹配，所以生成α5=54。

计算Λ5(z)=z5+100z4+73z3+85z2+51z+94及Λ5的根。构造二部图G1′，如图2所示。

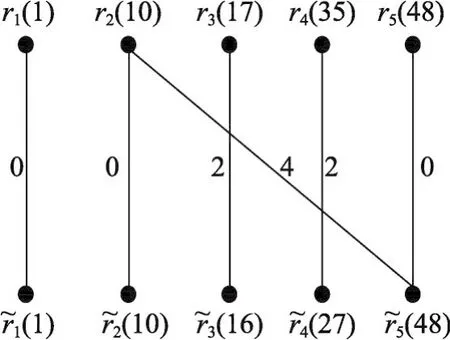
Fig.2 Bipartite graphG1′图2 二部图G1′

构造Gk和Gk′的交集，如图3所示。因此，x1在Mi,1≤i≤t中的次数分别为0,0,2,2,0。同理，计算x2和x3在Mi中的次数，分别为0,0,1,2,1和0,5,1,1,2。则

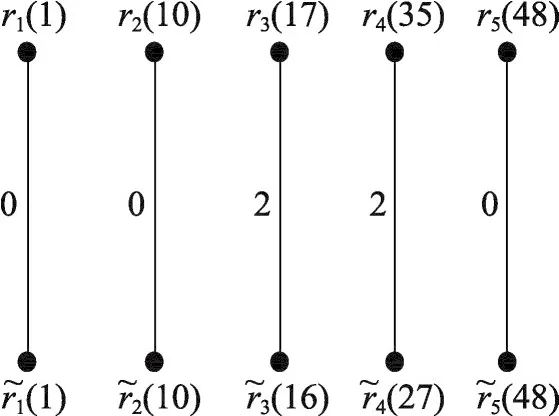
Fig.3 Bipartite graph图3 二部图

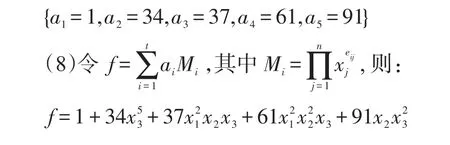
4 时间复杂度分析

本章讨论有限域上改进的稀疏多元多项式插值算法（算法2）的时间复杂度。需要考虑的主要因素有：

（1）计算多项式f的项数t，时间复杂度为O(t2)。

（2）计算多项式f的次数d，时间复杂度为O(d)。

（3）调用Berlekamp/Massey算法计算Λk至多n+2次，每次调用的复杂度为O(t2)。

（4）使用文献[13]中的技术求解Vandermonde系统，时间复杂度为O(t2)。

（5）求解Λk的根，时间复杂度为O(t2lbp)。

（6）计算变元xk的次数，时间复杂度为O(tlbt+dtlbt)。

（7）构造二部图Gk，时间复杂度为O(dt2)，求Gk和G′k的交集，时间复杂度为O(dtlbd)。

综上所述，改进算法的时间复杂度为：

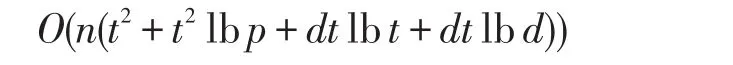
从时间复杂度分析可以看出，如果给定的项数界T和次数界D过高，会导致高计算复杂度，而改进算法花费较少的代价计算出多项式f的准确项数t及次数d，达到了此类型算法在后续操作上的最低时间复杂度。

5 数值实验

本章对改进算法和Javadi/Monagan算法进行性能比较。两种算法的编程环境均为Maple15，程序运行的硬件环境为Intel®CoreTMi7 2.20 GHz处理器和4.00 GB内存，操作系统为Windows 7。注意两个程序都是顺序执行，在确定变元x1，x2，…，xn的次数时未并行化。

本章给出了3组测试集的性能比较结果，使用的多项式都是随机生成的，比较的对象为CPU时间。黑盒中的多元多项式系数取自Zp，其中p=100 003。

测试集1本组测试集为6个包含3个变元的多元多项式。第i个多项式（1≤i≤6）使用如下的Maple命令随机生成：

其中，第i个多项式包含2i个非零项，d=20是多项式的准确次数。该组测试分别执行了改进算法和Javadi/Monagan算法，记录每个多项式在两种算法下的运行时间（单位：s），如表1所示。表头第1列Ex.表示例子的编号；第2列t表示项数；第3列括号中的百分比表示改进算法计算项数和次数的总时间与整个算法的运行时间的比值；改进算法无需给定项数界和次数界，Javadi/Monagan算法执行时，分别给定的次数界为D=20，D=30和D=30，项数界为多项式的准确项数T=2i(1≤i≤6)。表2和表3的设置同表1。

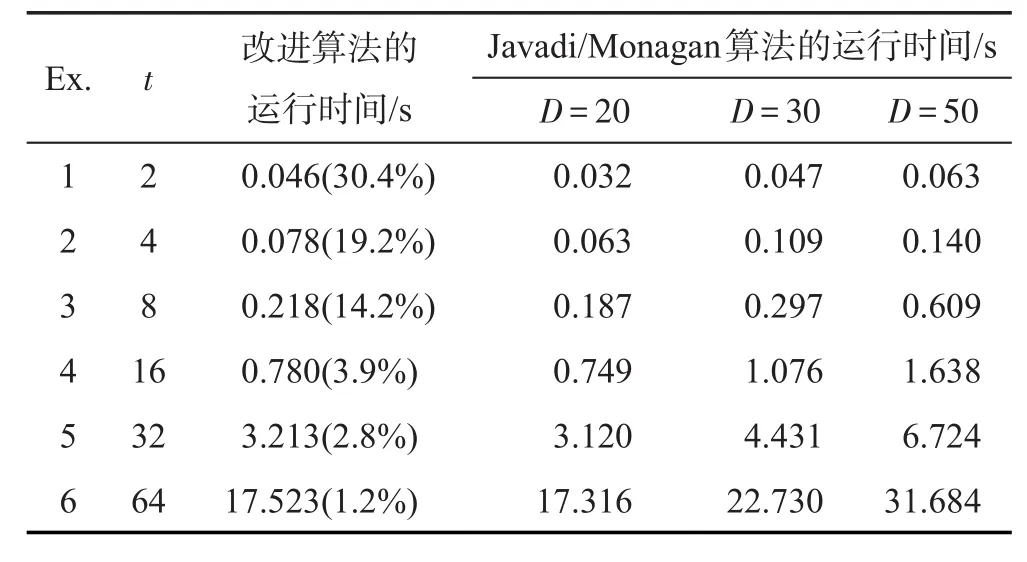
Table 1 Performance comparison of improved algorithm and Javadi/Monagan algorithm(n=3)表1 改进算法与Javadi/Monagan算法的比较(n=3)

从表1可以看出，随着i的增加，两种算法的执行时间也随之增加。在给定准确项数界T=2i和准确次数界D=20的情况下，Javadi/Monagan算法的执行时间优于改进算法，原因是改进算法利用3.1节和3.2节的方法分别计算出准确的项数和次数，不需预先给定这两个数据。显然，这两者的计算需要耗费一定的时间，但从表1中的第3列括号中的百分比可以看出，这两者的计算时间占整体运行时间的比值随着次数的增加越来越小，因而优势越来越明显。另一方面，随着次数界D的增加，Javadi/Monagan算法需要的执行时间也随之增加，当D较大时，算法的时间复杂度较高，这就是Javadi和Monagan在论文中提到的坏次数界问题（bad degree bound）。改进算法则有效地避免了这一问题。

测试集2本组测试集为6个包含6个变元的多元多项式。第i个多项式(1≤i≤6)使用如下的Maple命令随机生成：

表2给出了测试集2下改进算法和Javadi/Monagan算法的执行时间，表格的各项含义与测试集1相同。

测试集3本组测试集为6个包含12个变元的多元多项式。第i个多项式(1≤i≤6)使用如下的Maple命令随机生成：

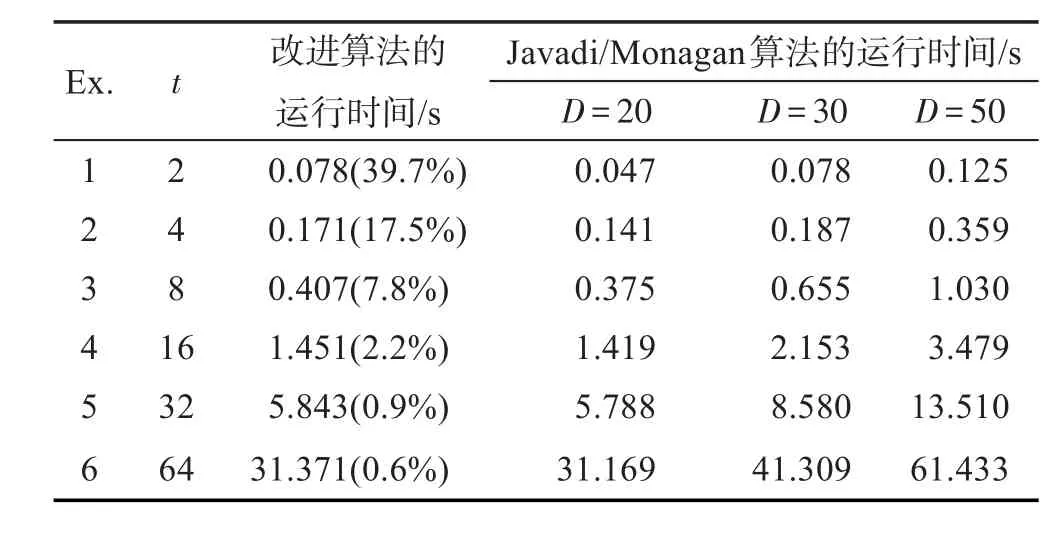
Table 2 Performance comparison of improved algorithm and Javadi/Monagan algorithm(n=6)表2 改进算法与Javadi/Monagan算法的比较(n=6)

表3给出了测试集3下改进算法和Javadi/Monagan算法的执行时间，表格的各项含义与测试集1相同。

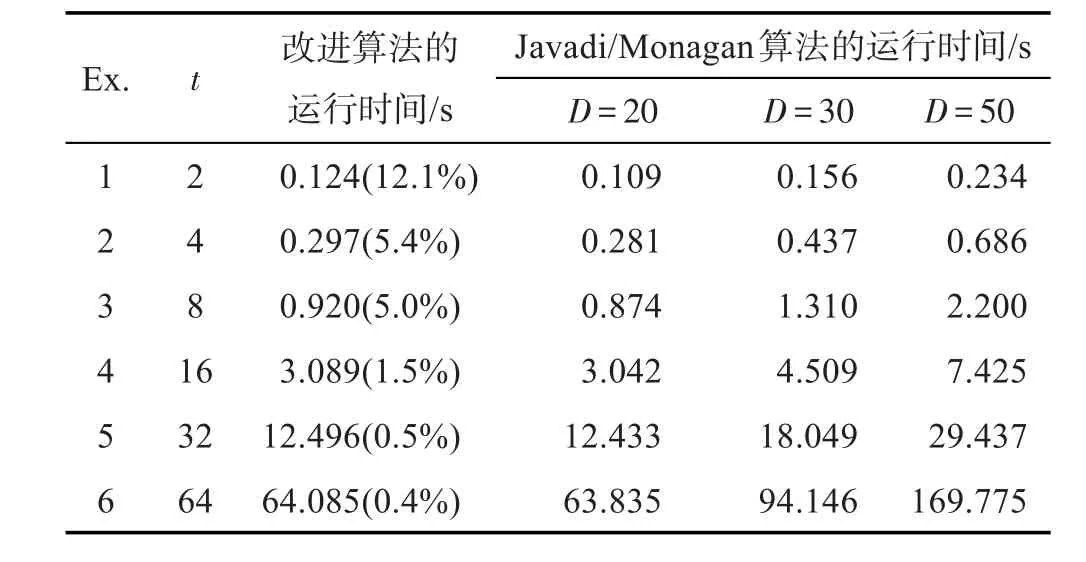
Table 3 Performance comparison of improved algorithm and Javadi/Monagan algorithm(n=12)表3 改进算法与Javadi/Monagan算法的比较(n=12)

从3组测试集可以看出，改进算法在确定插值多项式f的项数和次数上，花费的时间占整个算法运行时间的比例非常小，多项式规模越大，比例越小。如果Javadi/Monagan算法执行时，给定的次数界D越高，运行时间越长，而改进算法不受此影响。

6 应用实例

本章给出改进的Javadi/Monagan稀疏插值算法在几何问题上的一个应用。著名的Morley三等分定理描述如下：在任意三角形ABC中，对3个内角∠CAB、∠ABC和∠ACB分别进行三等分，相邻边交于三点P、Q、R，则三角形PQR必为一个正三角形，如图4所示。令a=BC,b=CA,c=AB,x=PQ=QR=RP,求x和a、b、c之间的关系。

Fig.4 Morley triangle图4 Morley三角形

根据题设中的几何关系和相关定理可知（推导过程略）：

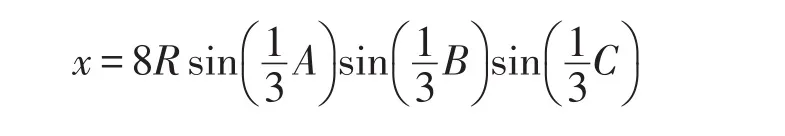
其中，R是三角形ABC的外接圆半径，有如下方程组：

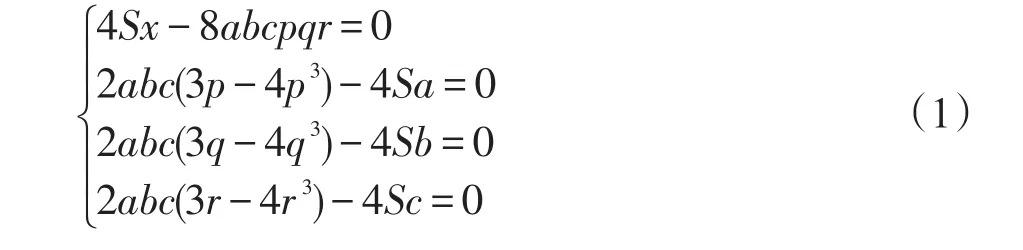
令x和a、b、c之间的关系为f(x，a，b，c)=0 ，如果利用结式等符号消元法，消去方程组（1）中的变元p、q、r，那么可得到x和a、b、c之间的关系f(x，a，b，c)。实际上，如果把a、b、c视为符号参数，消元过程因中间表达式膨胀而无法完成，若将a、b、c用实数α1、α2、α3进行替换，消元过程可顺利进行，结果是实例化的关系式f(x，α1，α2，α3)，例如（假定模p=105）：

如果视f(x，α1，α2，α3)为关于变元x的单变元多项式，则x的各次幂的系数是关于变元a、b、c的多元多项式，使用稀疏多元多项式插值恢复系数多项式，即可得到x和a、b、c之间的关系。在此例中，x的各个幂次的系数多项式的项数和次数都无法估计，如果采用原始的Javadi/Monagan算法，可能因为项数界和次数界设置不正确而导致无法得出结果或计算复杂度过高。若采用改进的Javadi/Monagan算法，可准确计算出各个系数多项式的项数和次数，最终得到的x和a、b、c之间的关系式：

此例中，f(x，a，b，c)共有804项，其中x27的系数多项式的项数为45，次数为32。x25的系数多项式的项数为28，次数为34。其余系数多项式的指标不再赘述。

在结式消元、GCD计算、几何组合优化、信号处理等问题上，很多情况下无法预知目标多项式的次数和项数，故改进算法针对这些问题更具实用性。

7 结束语

稀疏多元多项式插值是很多计算机代数算法的子函数，也广泛应用于信号处理、压缩感知、图像处理等领域。在给定项数界T和次数界D较高的情况下，改进算法可有效降低Javadi/Monagan算法的计算复杂度。进一步，改进算法消除了传统插值算法中必须预先给定插值多项式项数T和次数D的必要条件，更具实用性。

3.3节的算法2给出了有限域上改进的Javadi/Monagan稀疏多元多项式插值算法，其中两个循环体（算法2中步骤4到步骤8及步骤10到步骤19）的计算任务可并行化处理，一是生成关于变元z的单变元多项式Λ1(z)，Λ2(z)，…，Λn+1(z)，可分为相互独立的n+1个子任务，二是确定变元x1，x2，…，xn在各个单项式中的次数，可分为相互独立的n个子任务。假设有q个计算内核的集群系统，每个内核可独立承担上述计算Λj(z)，j=1，2，…，n+1 的 (n+1)/q个子任务，以及计算变元xj，j=1，2，…，n在各个单项式Mi，i=1，2，…，t中的次数eij的n q个子任务，计算结果可保存在一个文件中，最终可确定黑盒多项式f中的各个单项式。在后续工作中，拟将改进算法进行并行化处理，以进一步提高稀疏多元多项式插值算法的效率。