奇妙的圆形空腔内的匀强场

严灿云

(江苏省通州高级中学，江苏 通州 226300)

在高中物理竞赛的学习中,研究了一类重要的问题,就是“场”,其中包括引力场、电场、磁场.这些场的空间分布与场源有着很重要的关系.本文中笔者跟大家分享一类特殊的场:圆形空腔中的匀强场.

1 圆形空腔中的匀强引力场

如图1,行星上有一个以表面A点到球心O作为直径的球形空腔,设行星密度为ρ,半径为R.现从A点处无初速的掉入一物体,试求物体从A点掉到O点所用的时间.

解析:要解答这个问题,需要知道球形空腔内的引力场的重力加速度.如图2,设空腔球心为O′,在空腔内任取一点P,P点的重力加速度可以理解为密度为ρ的实心大球和密度为-ρ的实心小球在P点的重力加速度的合成.

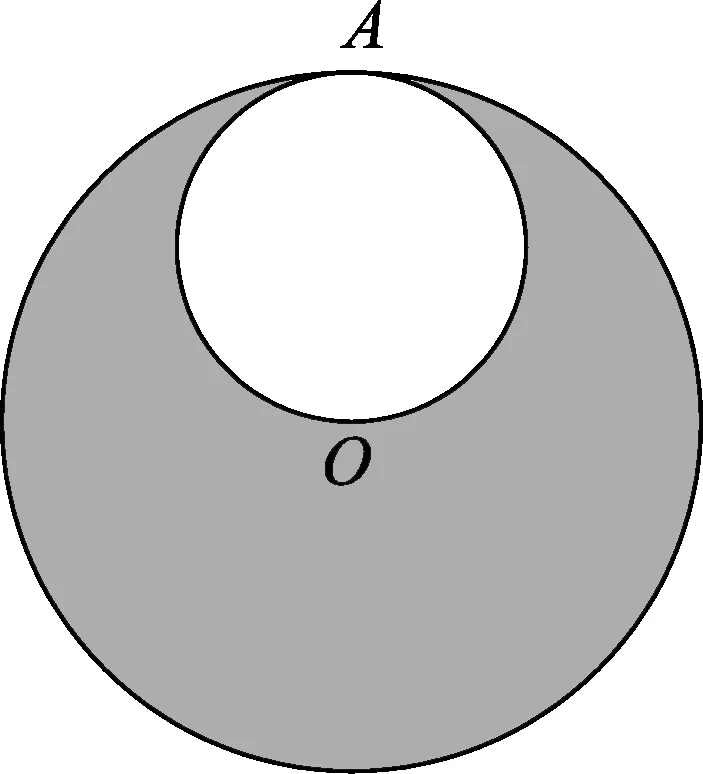
图1

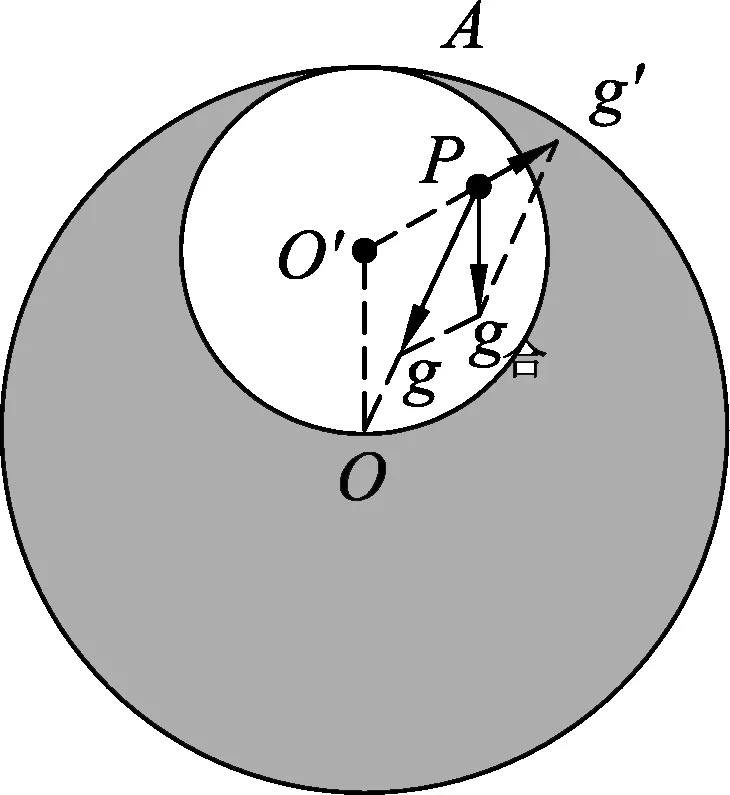
图2

实心大球在P点产生的重力加速度

实心小球在P点产生的重力加速度

故

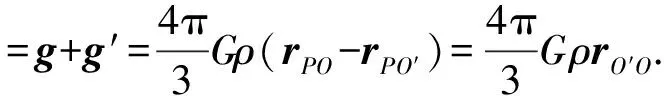
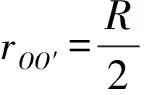
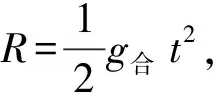
图3

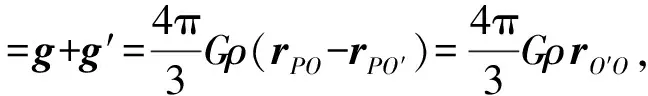
2 圆形空腔中的匀强电场

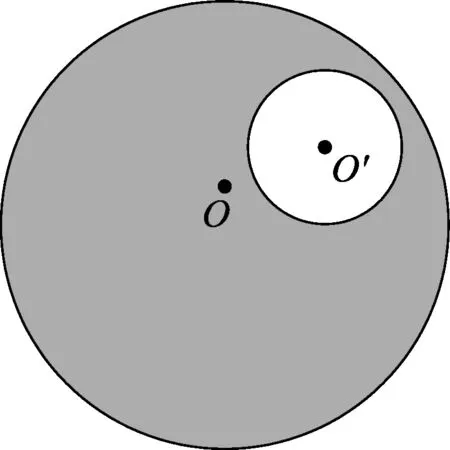
图4

如图4所示,在半径为R,电荷体密度为ρ的均匀带电球体内部挖去半径r的一个小球,小球球心O′与大球球心O相距为a,试求O′点处的电场强度,并证明空腔内电场均匀.

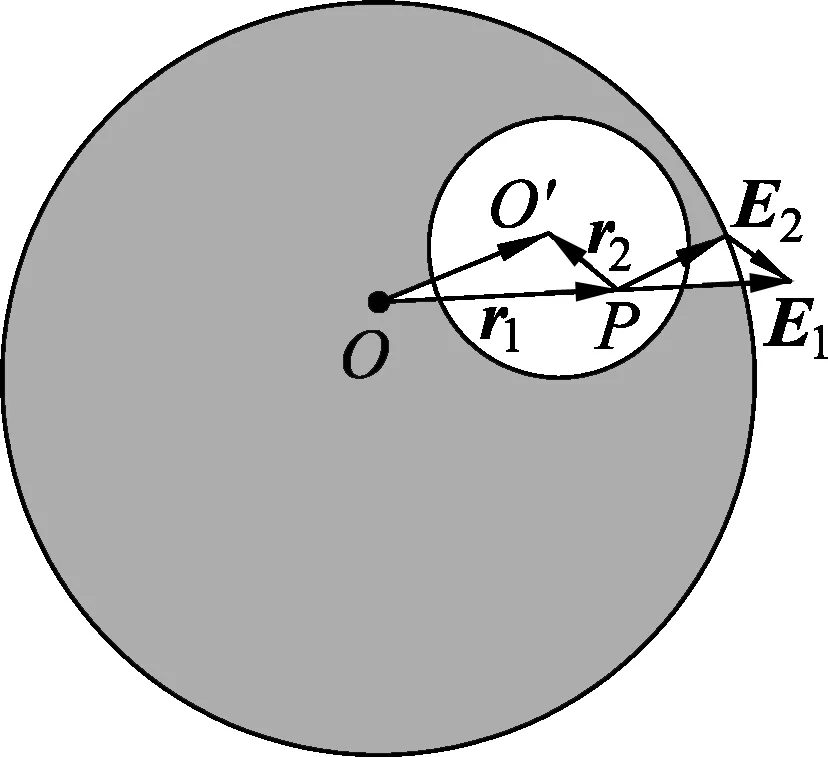
图5

解析:圆形空腔中的电场,亦可以看成是电荷体密度为ρ的大球和电荷体密度为-ρ的小球共同产生的电场的合成.如图5所示,在空腔内任取一点P,大球在P点的场强为

同理,小球在P点的场强为

故

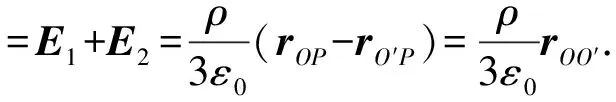
3 圆柱形空腔中的匀强磁场

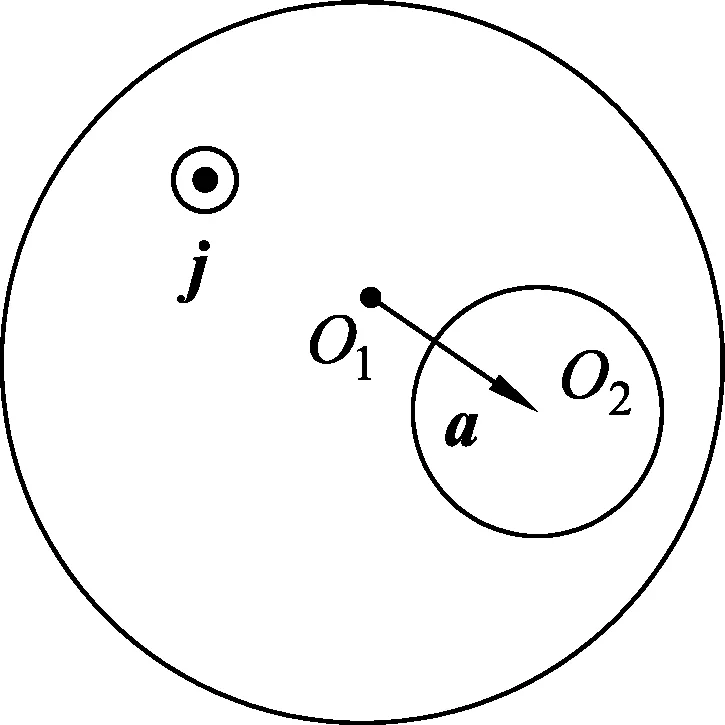
图6

一半径为R1的无限长金属圆柱体内挖去一半径为R2的小圆柱体,两柱体的轴线平行,俯视图如图6,圆心分别O1和O2,rO1O2=a.金属圆柱内有沿轴向流出纸面外的电流,电流密度均匀且为j.求小圆柱面内(空腔内)磁感应强度.

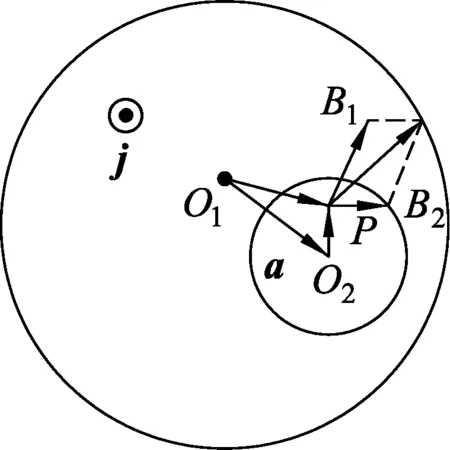
图7

解析:空腔内的磁场可以看成是大圆柱内流出的电流和小圆柱内流入的电流产生的磁场的合成.无限长通电直导线周围的磁场的求解可以用环路定理求解,空腔内任取一点P,如图7,大圆柱内的电流在P点产生的磁场可由环路定理求解,B1·2πrO1P=μ0j·πrO1P2,可得

同理,小圆柱在P点产生的磁场为

P点的合磁场为

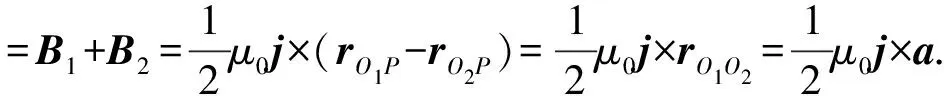
4 圆柱形空腔中的匀强感生电场

一无限长圆柱,偏轴平行的挖出一个圆柱空间,两圆柱轴间距OO′=d,图8所示为垂直于轴的截面.设两圆柱间存在均匀磁场,磁感应强度B随时间t线性增长,即B=B0+kt.现在空腔中放一与OO′成60°角、长为L的金属杆AO′B,求杆中的感生电动势.

图8

解析:先求解空腔内的感生电场.圆柱内的感生电场可以看成是大圆柱内的垂直于纸面向里增加的磁场和小圆柱内垂直于纸面向外增加的磁场共同产生的.在空腔内任取一点P,P点感生电场的矢量图如图9,由法拉第电磁感应定律可求得大圆柱内变化的磁场在P处产生的感生电场,得

同理,小圆柱内变化的磁场在P处产生的感生电场,

P处的合电场为

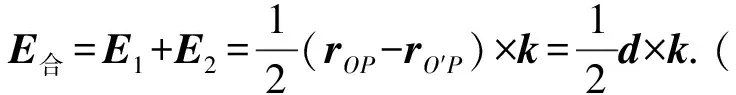
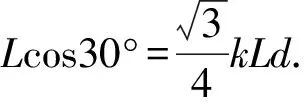
图9

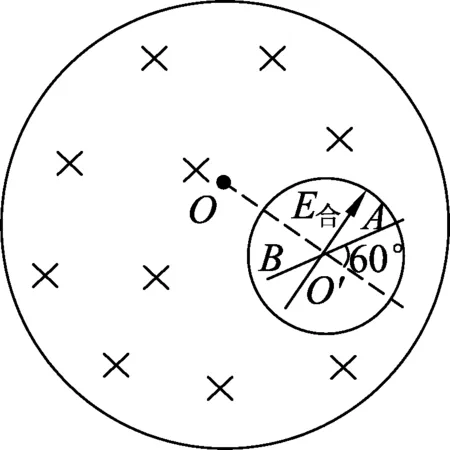
图10

结语:上面讨论的4种情形,其实对应了中学阶段学习的4种场,对应这4种不同的场居然都有圆(柱)形空腔内的匀强场存在,不得不说是件很奇妙的事情,但是,回头看看之所以会有这样的结论,其本质是因为场强和位置矢量之间是一次函数关系;另外,他们的处理方法相似,都是采用 “正负抵消”法来处理空腔内的问题的．