椭圆运动中万有引力定律表达式的推导兼谈卫星椭圆运动的运行参量及应用

赵曰峰

(大连市第八中学,辽宁 大连 116021)

1 椭圆运动轨迹的曲率半径

天体绕太阳椭圆运动轨迹方程表示为

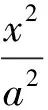
椭圆参数方程表示为

x=asinωt，y=bcosωt.

(1)

(1)式对时间求导有

(2)

(2)式对时间求导有

-bω2cosωt.

(3)

在t时刻,天体运动到某一位置(x,y),如图1(a)所示.该点处切线斜率表示为

(4)

(4)式结合sin2i+cos2i=1得

则在该点处的速度大小

如图1(b)所示,向心加速度大小

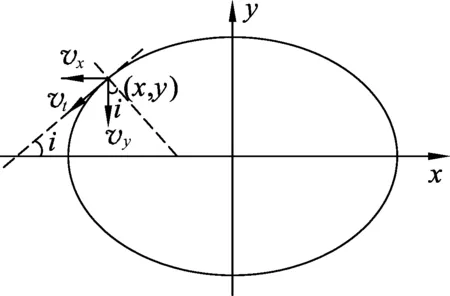
(a) (b)

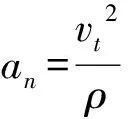
(5)

2 万有引力表达式的确定

天体椭圆运动轨迹上任一点(x,y),如图2所示.该点切线斜率为

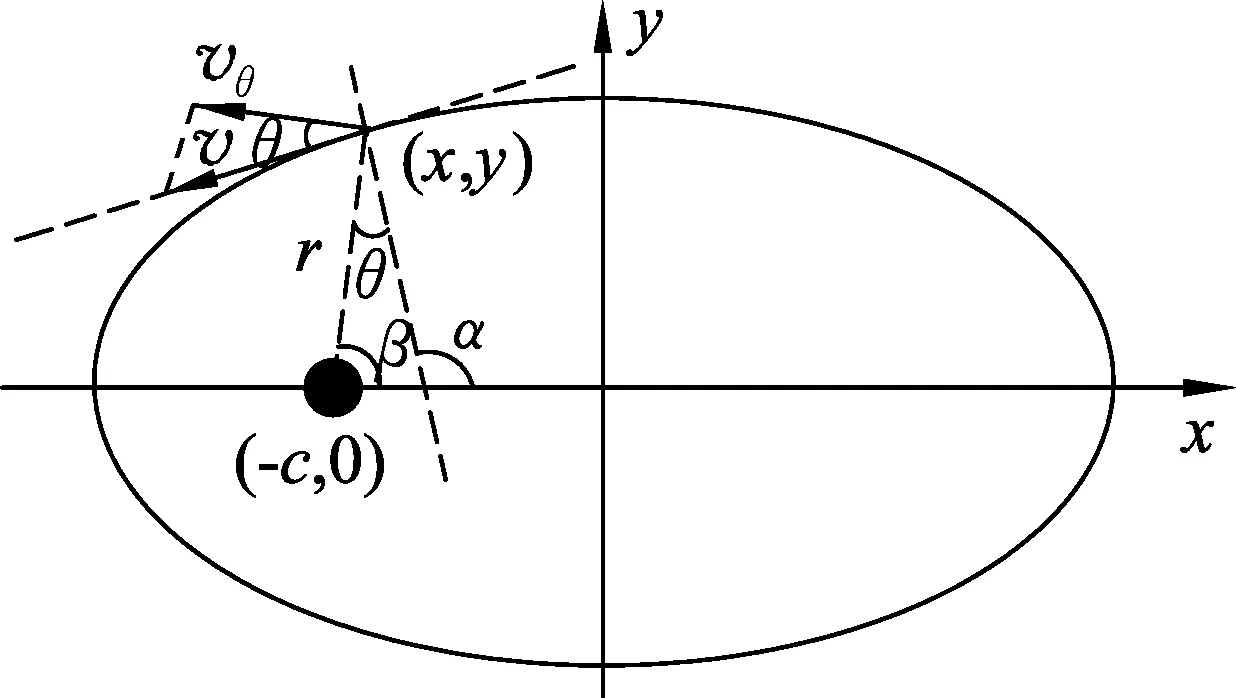
图2

该点法线斜率为

天体在该点引力方向斜率为

该点处法线方向和天体所受引力方向夹角θ满足

(6)

(6)式结合sin2θ+cos2θ=1得

(7)

根据开普勒第二定律知在极短时间Δt内,满足

(8)

由椭圆面积S=πab和开普勒第二定律有

(9)

又知

vθ=vcosθ.

(10)

由牛顿第二定律和向心力公式有

则太阳对行星的引力大小为

(11)

其中

(12)

行星围绕太阳运动过程中,太阳吸引行星,行星同样也吸引太阳,从相互作用的角度而言,二者的地位是相同的.对于行星对太阳的引力F′而言,太阳是受力星体,因此F′应与太阳质量M成正比,与行星、太阳距离的二次方成反比,即

(13)

在一线教学过程中,笔者认为可在第2节“太阳与行星间的引力”后适当讲授椭圆运动中万有引力表达式的推导,帮助学生区分引力半径r和曲率半径r(轨道半径)的不同、明确万有引力和向心力的关系,同时了解椭圆运动,为卫星椭圆运动相关运行参量确定和处理卫星变轨问题奠定基础.

3 卫星椭圆运动的相关参量及应用

图3

关于天体的椭圆运动,以卫星绕地球运转为例,运动轨迹如图3所示.本文主要推导卫星近地点和远地点的速度、角速度、加速度的表达式.

由(5)式可知,卫星近地点和远地点的曲率半径

(14)

卫星在近地点和远地点的引力半径分别为

rQ=a-c;rP=a+c.

(15)

卫星在近地点和远地点处万有引力充当向心力.

近地点:

(16)

远地点:

(17)

由(14)-(16)式联立解得近地点的速度、角速度、加速度分别为

(18)

(19)

(20)

由(14)(15)(17)式联立解得远地点的速度、角速度、加速度分别为

(21)

(22)

(23)

当椭圆变为圆即c=0时,(18)-(23)式变为圆周运动情形下的速度、角速度、加速度表达式.

应用1.导弹弹头发射过程中最高点处的速度及加速度.

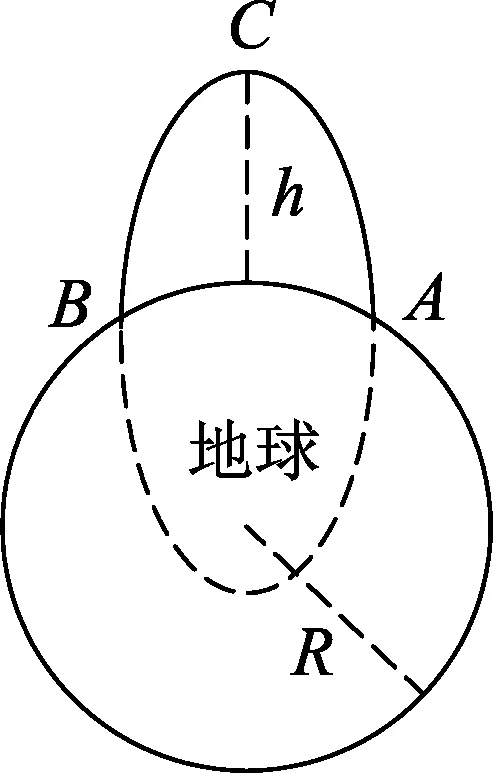
图4

例1.如图4所示,发射远程弹道导弹,弹头脱离运载火箭后,仅在地球引力作用下,沿椭圆轨道飞行,击中地面目标B.C为椭圆轨道的远地点,距地面高度为h.已知地球半径为R,地球质量为M,引力常量为G.关于弹头在C点处的速度v和加速度aC,下列结论正确的是

解析:由于C点位于椭圆轨道的远地点,设椭圆轨道长轴为2a,焦距为2c,由图4知a+c=R+h.

由(21)-(23)式中远地点的速度为

远地点的加速度表达式为

所以(B)选项正确.

应用2:卫星运行速度、加速度大小的比较及卫星发射过程中的变轨问题.

图5

例2.如图5所示,3个质量相同卫星分别在近地轨道1、椭圆轨道2、高圆轨道3轨道运行.近地轨道1上的运行速度、加速度分别为v1、a1,椭圆轨道2近地点Q(轨道1和2的交点)、远地点P(轨道2和3的交点)的速度分别为vQ和vP,加速度分别为aQ和aP;高圆轨道3上的运行速度、加速度分别为v3、a3,请比较: (1)v1、vQ、vP和v3的大小; (2)a1与aQ的大小,a3与aP的大小.

显然卫星速度大小关系为vQ>v1>v3>vP.

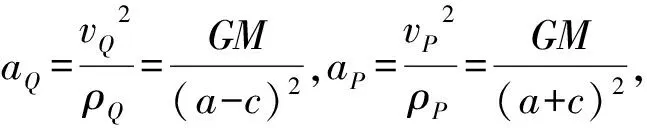
显然Q和P点加速度大小满足aQ=a1,aP=a3.

由例2可知,当发射高轨道卫星时,可先将卫星发射到半径为rQ的近地轨道1上,如图5所示,运行速度为v1;当卫星运动到Q点时,卫星发动机点火加速到vQ,使卫星从轨道1进入椭圆轨道2,此时Q点为卫星椭圆轨道的近地点;卫星运动到椭圆轨道远地点P时(速度大小vP),卫星发动机再次点火加速到v3,使卫星进入轨道为rP的高圆轨道.目前我国发射的高轨道卫星、嫦娥系列探测器都采用上述发射方式,使卫星或探测器进入预定轨道.

4 结束语

本文通过物理规律、结合数学推演的方式严谨推导出了万有引力表达式,同时为后续学习奠定基础.高中物理教学更多的是从实际情景中抽离出的理想模型,然而多数学生内心渴望一种严谨缜密的思维梳理和推导过程,只有亲身经历这样的过程,才能被物理的逻辑美所吸引,从而保持对物理学科的热情,激发深入学习的兴趣,进而培养物理学科核心素养.

另一方面,目前我国“神州、天宫、嫦娥”系列工程正在蓬勃发展,取得了卓越的成就.这使万有引力与航天成为考试热点,特别是卫星发射问题,涉及一些高等数学知识,综合性强,这也是难点.而教材所设计的内容浅显,需要深入挖掘,笔者通过本文希望起到抛砖引玉的作用.