基于陀螺系的速率偏频惯性测量组合标定方法

江一夫，陈 勇

（中国航天科技集团第十六研究所，西安710100）

0 引言

通常情况下，激光陀螺和加速度计敏感轴的方向与捷联惯测组合基准面所确立的坐标轴方向是大致平行或正交的。针对这类直装捷联惯导系统，主要有三类标定方法，包括分立式标定方法［1］、基于误差解耦的迭代式拟合估计方法［2⁃4］及基于零速量测的 Kalman滤波标定方法［5⁃7］。目前，这些方法都趋于成熟，能较好地解决惯性测量组合的定期维护问题。

为了能够基于一个转位机构使得三只激光陀螺同时敏感到旋转角速率，速率偏频惯导系统中的惯性仪表往往采取斜置的安装方式［8］。早在20世纪80年代，国外便开始研制速率偏频激光陀螺系统［9⁃11］，但未见惯性仪表标定方面的相关文献。在国内，文献［12］提出了结合光学测量标定陀螺安装误差角的方法，这种方法利用速率偏频转台自身的旋转角速率对陀螺刻度系数和常值漂移进行了简易标定。文献［1］提出了一种斜装惯性仪表的标定算法，这实际上是一种简单的、基于壳体基准系的分立标定方法。文献［13］提出了速率偏频系统的Kalman滤波标定方法，其原理与直装系统类似。文献［14］提出了一种基于模值不变原理的标定方法，但是其陀螺零偏和加速度计标定流程繁琐而复杂。

对于斜装系统，常规标定方法均是理论可行的。但在工程实际应用中发现，斜装系统存在其独有的、不可忽视的问题，即标定结果存在较大的激光陀螺标度因数误差。本文以分立式标定为例，分析了造成陀螺标度因数标定误差的原因，认为速率偏频系统独有的倾斜安装方式造成了旋转轴与陀螺敏感轴之间的大角度安装偏差，导致常规标定方案无法完全激励出陀螺标度因数误差。

为了解决传统标定方法不适应斜装惯导系统的问题，本文提出了一种新的基于陀螺系的系统级整机标定方法。由于陀螺敏感轴具有较高的稳定性，相对于以加速度计作为参考坐标系的标定方法，该方法确保了导航过程输出空间姿态基准的绝对稳定性，同时有利于提高激光陀螺安装角的标定精度和标定稳定性。

1 速率偏频惯导系统的模型

为了能够基于一个旋转台使三轴陀螺都能敏感到旋转角速率，从而实现速率偏频，系统中的激光陀螺需采用如图1所示的倾斜安装方式。

图1 速率偏频激光陀螺惯导系统的安装方式示意图Fig.1 Mounted scheme of rate-bias laser-gyro inertial navigation system

定义g系为由三轴陀螺敏感轴构成的非正交系，定义 go系（Oxgoygozgo）为陀螺正交参考坐标系，xgo轴与陀螺敏感轴xg重合，ygo轴在xgyg平面内，zgo轴与xgo轴、ygo轴构成正交系。在实际过程中，非正交系g与go系之间存在小角度的安装误差。定义p系为转位机构的台面坐标系，zp轴与转位机构的旋转轴重合，xp轴与xgo轴在转台台面上的投影重合，yp轴与zp轴、xp轴构成正交系。

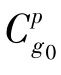
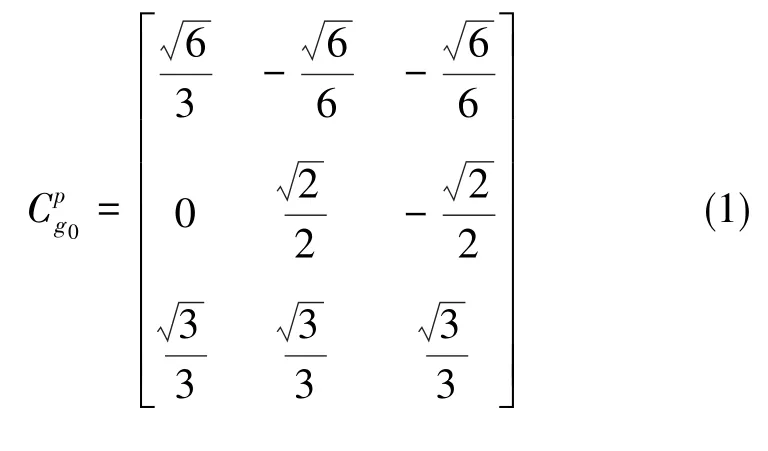
2 常规标定方法存在的问题

针对斜装系统，一些学者提出直接采用分立式标定方法。其中，激光陀螺采用速率标定方式，其标定模型如下

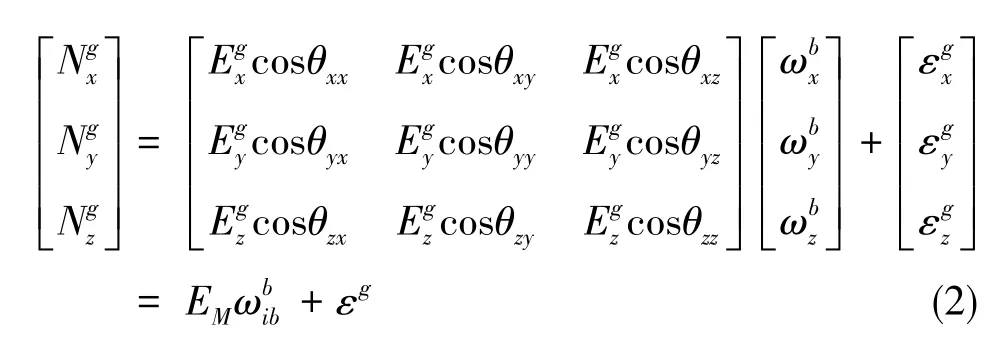
由于b系是正交的，故式（2）标定矩阵每行的模值为对应的标度因数［15］，以x轴为例有

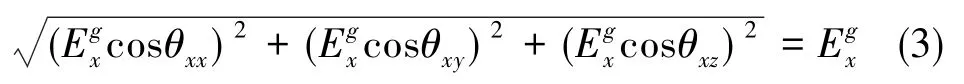
分立标定均以外界物理基准坐标系作为参考坐标系，但是由于加工问题，捷联惯组的标定工装或其本身的定位面存在不正交误差。同时，在速率标定三轴依次朝上的过程中，由于旋转式惯导系统转轴间隙的存在，三轴惯性仪表系相对外部基准坐标系发生了变化，这实际上带来了较大的安装角误差。

假设 θxx不存在误差，而 θ′xy和 θ′xz都存在 10″的误差，三者的理想值为54.7356°，θxy为114.0948°，θxz为 135.0000°。根据式（3），可估算出将存在4.2×10-5的误差。当系统为直装时，θxx的理想值为0°，θxy的理想值为90°，θxz的理想值为90°，上述安装角误差仅引起了2.4×10-9的标度因数误差。因此，这种速率标定方法无法准确标定激光陀螺标度因数的现象是斜装速率偏频系统所独有的。

同样，利用迭代式拟合估计和Kalman滤波标定方法计算斜装系统的标定参数，发现激光陀螺标度因数存在2×10-5左右的误差，这与直装惯导系统的多位置翻滚标定方案无法充分激励斜装系统中的陀螺标度因数误差而导致标度因数误差和安装角误差无法实现准确分离有关。而一般系统级标定方法的安装角标定精度较高，因而相对分立式标定方法，系统级标定中的标度因数误差较小，但是仍然不能满足使用要求。为了解决这个问题，本文提出了一种新的基于陀螺系的系统级标定方法。

3 基于陀螺系的标定方法

3.1 三轴陀螺标定方法

假设陀螺的输出模型如式（4）所示

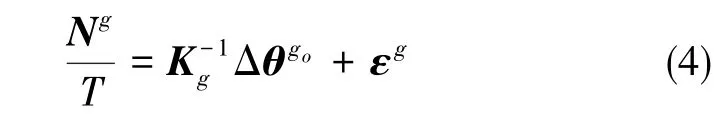
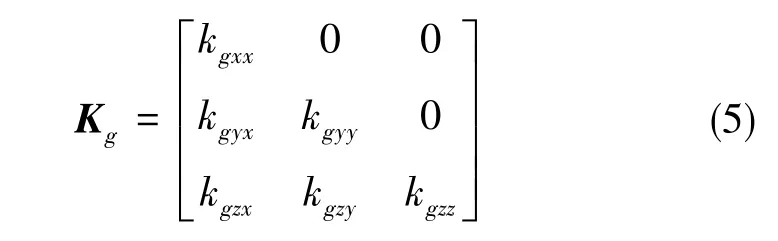
由于正反转消除了陀螺零偏和地球自转的影响，对正反转n圈过程的陀螺输出进行积分并相减，得到的旋转矢量模值大小必然为4nπ，即有

采用解非线性方程组的最优化算法［16］，通过多次迭代运算可求得Kg中的所有参数。为了减少计算量，本文采用文献［17］中的最小二乘算法，令

在Kg已知的条件下，利用最小二乘算法可以计算出εgu。

3.2 三轴加速度计标定方法

以陀螺正交系go建立加速度计标定模型

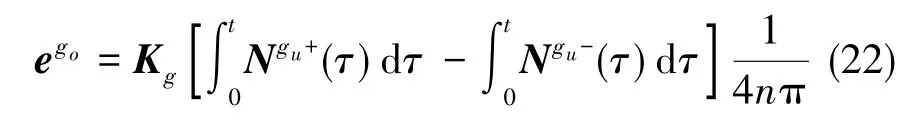
使IMU外箱体三轴分别朝上和朝下，可以得到如式（22）所示的6组18个方程，通过最小二乘算法可以解出三轴加速度计需要标定的所有参数。

4 试验结果及验证分析

采用陀螺零偏稳定性优于 0.003（°）/h、加速度计偏置约为50μg的单轴旋转速率偏频惯导系统进行标定试验。以单陀螺在陀螺测试工装上的标定结果作为参考基准，X、Y、Z 3个90型激光陀螺的标度因数参考值分别为：2.14426163＾/（″）、2.14510797＾/（″）和 2.14456973＾/（″）。其中，＾/（″）表示脉冲每角秒。

4.1 常规标定方法的试验结果

分立标定以壳体定位面确定的坐标系为输出参考系。其中，陀螺采用速率标定方法，通过调整惯组的摆放方向使其沿惯组壳体坐标轴各正反旋转一整周，标定过程的陀螺原始采样脉冲经数字滤波后的变化曲线和标定结果如图2和式（23）所示。

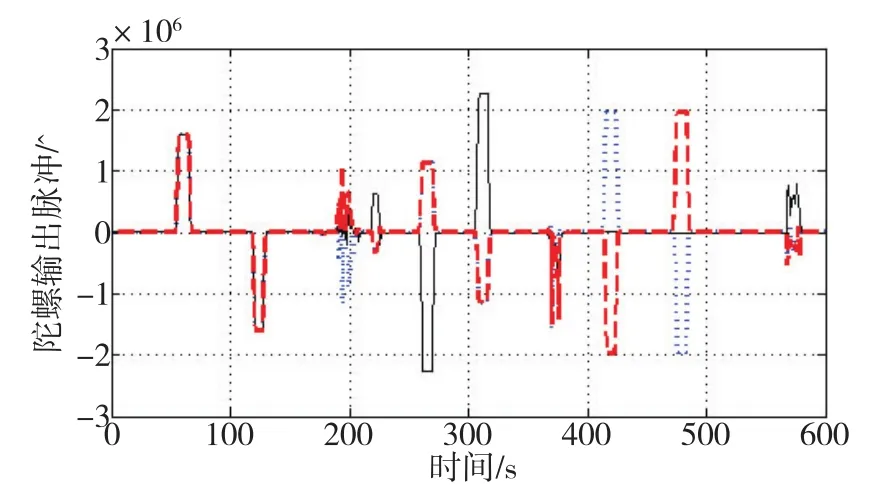
图2 速率标定过程的激光陀螺输出脉冲Fig.2 Output pulse of laser gyros during rate-calibration test

采用文献［1］中的计算方法，对矩阵EM的每行求模值，可得到3个陀螺的标度因数［2］，分别为：2.14398708＾/（″）、2.14510855＾/（″）、2.14482703＾/（″）。

采用系统级多位置Kalman滤波标定方法对斜装速率偏频系统进行标定，加速度计的原始脉冲输出如图3所示，标定结果如式（24）和式（25）所示。

图3 速率偏频系统多位置翻滚标定中的加速度计输出脉冲Fig.3 Output pulse of accelerometers during multi-position systematic calibration test

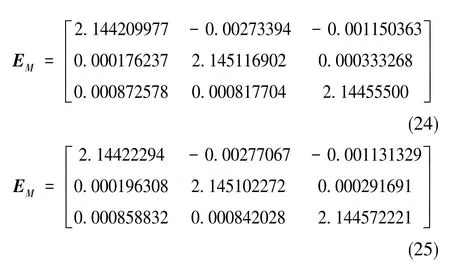
将用常规标定方法进行的三轴陀螺标度因数的标定结果及误差进行整理，可得如表1所示的结论。

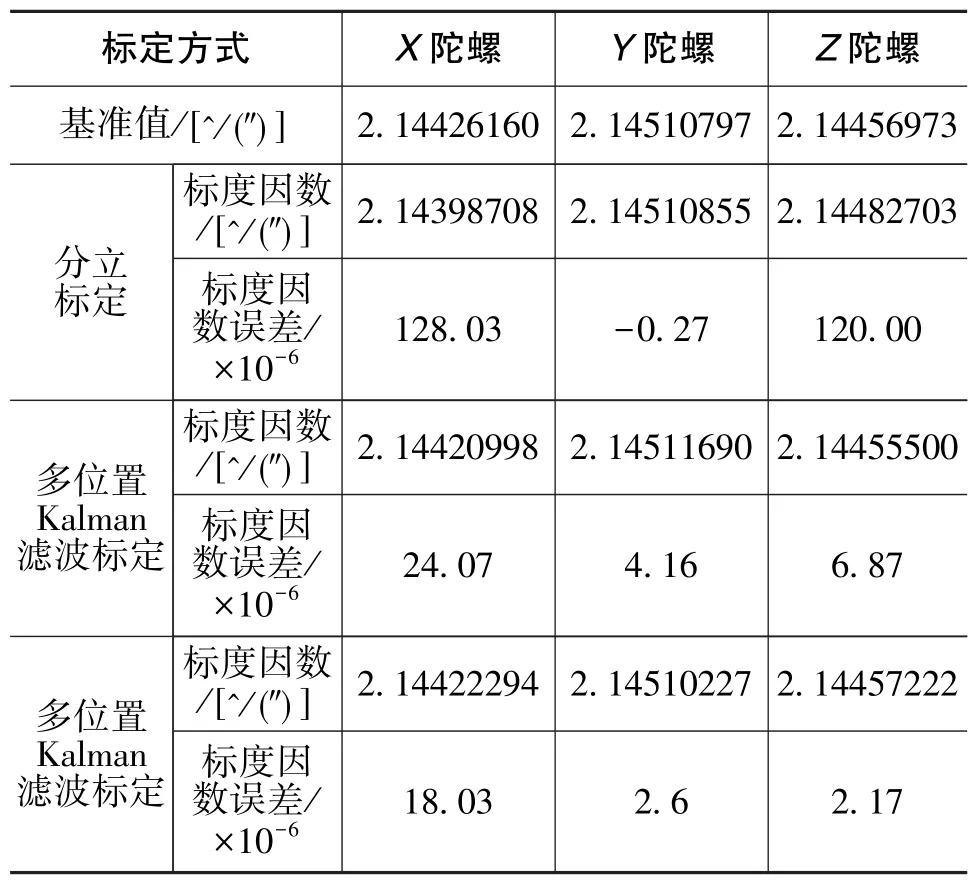
表1 常规标定方法的陀螺标度因数结果及误差Table 1 Calibration result and error of tradition calibration method

4.2 陀螺系标定方法的试验结果

为了验证本文所提出的陀螺系标定方法的有效性和长间隔时间下的标定稳定性，在7个月的时间内进行了4次标定，其标定结果如表2所示。

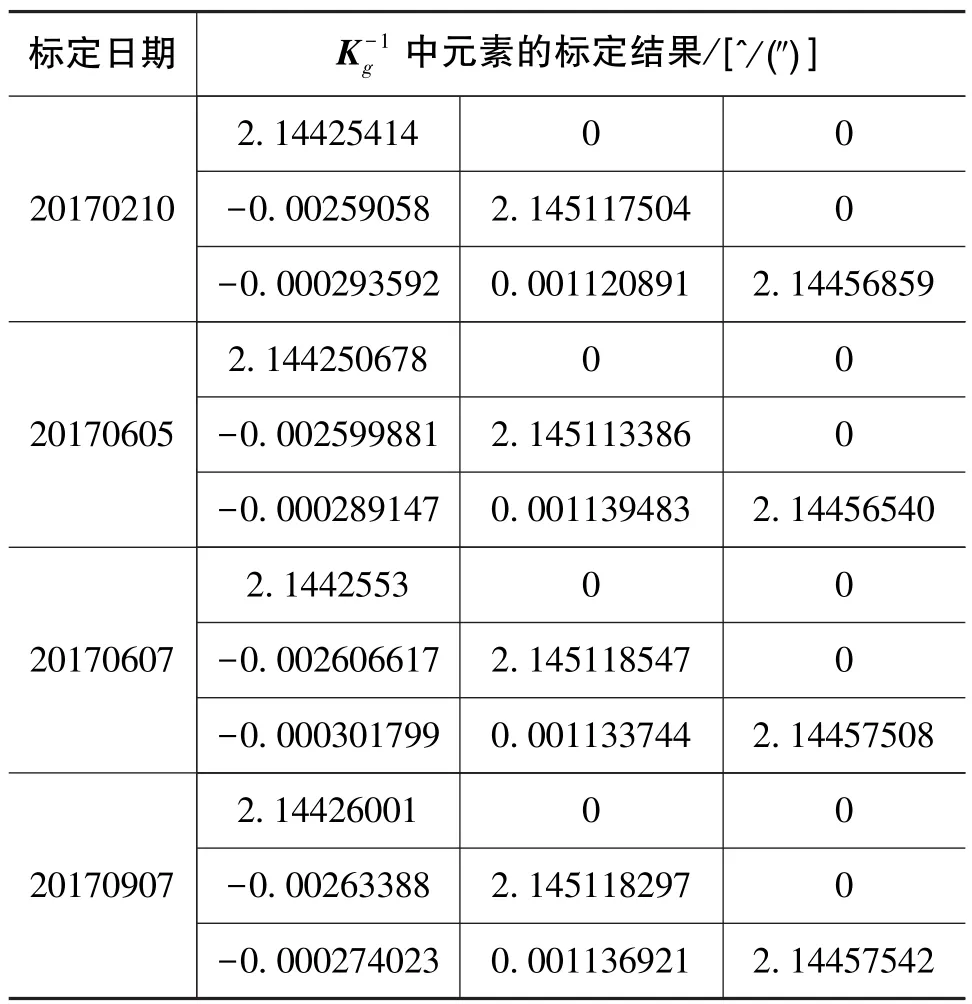
表2 陀螺系标定方法的标定结果Table 2 Calibration results of gyro-axis-based calibration method

4.3 试验分析和结论

从表1中常规标定方法的试验结果可以看出，以单陀螺测试结果为基准，在分立标定中，X陀螺存在约1.28×10-4的标定误差，Z陀螺存在约1.2×10-4的标定误差，远远超出了高精度导航系统的允许范围。同时，试验结果也验证了前文的理论分析结论，即分立标定中安装角误差会引起较大的陀螺标度因数误差。而常规直装惯导采用的多位置翻滚Kalman滤波标定方法在速率偏频系统中仍然不能完全解决陀螺标度因数精确标定的问题。从表1的结果可以看出，X陀螺的标度因数误差并未完全收敛，而是存在约2×10-5的误差，仍然不能满足高精度惯导系统的使用要求。

针对本文提出的基于陀螺系的标定方法，从表2的结果可以看出，以单陀螺测试结果为基准，7个月内的4次标定的陀螺标度因数的最大误差为5.2×10-6，重复性优于4×10-6，陀螺安装角标定重复性优于4.2″，说明了该标定方法的有效性和相对较高的长时间稳定性。

5 结论

本文从理论分析和工程实际出发，说明了常规标定方案无法实现速率偏频系统激光陀螺标度因数精确标定的问题，认为引起该现象的深层原因主要在于速率偏频系统独有的倾斜安装方式，其小量安装角误差仍然会引起较大的标度因数误差。为了解决该问题，本文提出了一种新的基于陀螺系的标定方法，主要利用旋转矢量模值不变原理及旋转矢量与重力矢量之间的关系，来实现三轴陀螺和三轴加速度计参数的估计。试验证明，该方案不但能实现对速率偏频斜装惯导系统的精确标定，而且陀螺标度因数和安装角的标定结果具有相对较高的长时间稳定性，证明了该方案具有较高的工程应用价值。