从算术思维到代数思维的跋涉之旅
刘丽珍
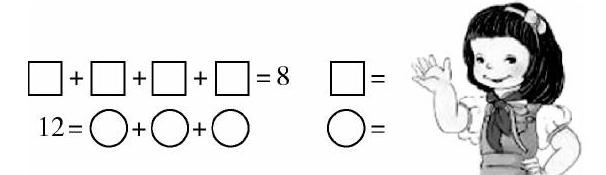
【摘要】代数思维的早期渗透是我国当前小学数学教学改革的一个主要方向,本文主要从低年级计算教学中的三个方面,进行早期代数思维培养的研究.
【关键词】代数思维;早期;渗透
在中小学数学教育中,代数思维是数学的核心思想.代数思维的早期渗透是当前国际数学教育界的一个普遍认识,也是我国当前小学数学教学改革的一个主要方向.
一、什么是代数思维
算术思维和代数思维是数学学科的两种主要思想.算术思维是特殊化思维,研究的对象是数字及其计算与拆合,体现的是“过程性观念”;而代数思维是一般化思维,研究对象是代数式及运算与变换,体现的是“结构性观念”.
二、当前代数思维教学中存在的问题及原因分析
问题:小学重视算术思维的培养,忽略代数思维的培养,后续学习困难.
原因:在早期学习中,没有建立起足够的代数思维基础.
对策:在小学低年级教学中,虽然没有出现正式的代数形式,但要充分挖掘教材里蕴藏的代数思维“雏形”,有序地对学生进行渗透,帮助学生积累代数思维的经验,培养学生对代数结构与关系的理解.
三、代数思维早期渗透的实践研究
笔者站在数与代数领域的整体高度,对人教版小学数学整套教材进行梳理后发现,在低年级计算教学中,代数思维可从以下两个方面进行早期渗透.
(一)在互逆运算中渗透代数思维
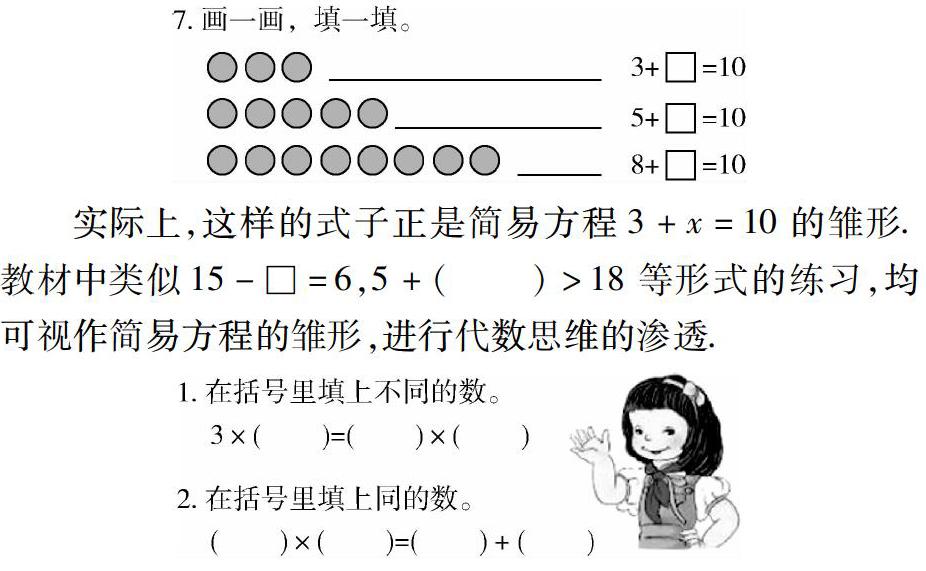
在低年级加减法的逆运算练习中,就蕴含着代数思想,只是它们称作“未知数”,并未称作“方程”而已.如一上P63第7题,学生初步感知到( )可代表一个数,算术法是:10-3=?;代数法是:接着数,3个圆形加上几个等于10个?
实际上,这样的式子正是简易方程3+x=10的雏形.教材中类似15-□=6,5+( )>18等形式的练习,均可视作简易方程的雏形,进行代数思维的渗透.
(二)在等式计算中渗透代数思维
构建数字等式的练习把学生运算能力和代数思维的培养整合在一起.如二上P65的思考题,学生拘泥于具体运算,受等号是“输出结果”的影响,常认为等号后面的数是前面一个算式的得数,不会把“3×2”看成是一个结果,于是就出现这样的错误:3×2=(6)×3.因此,教师要引导学生超越算术思维,识别出算术里蕴含的代数思想,把等号理解成表示平衡关系的符号,实现“=”由“输出结果”向“相等关系”的转变,促使学生不会看到算式之后条件性的写上答案,而会运用关系性思维辨别其中的关系.
由“等号的程序性质”向“等号的关系性质”转化,恰恰是学生由算术思维向代数思维发展的标志之一.
(三)用简单的符号代表未知数
数字符号是对生活中各种物体个数的抽象概括,代数式则是对各种数字符号的抽象概括.低年级教材中的图形等式,就是代数式的“雏形”.如二下P26的思考题,教学时,先让学生弄懂□可以表示一个数;再利用乘法的含义,推算出它所代表的数;最后,让学生体验“代入”思路,构造图形等式,从而体验等式性质.这样,在代数思想的指导下,学生思维有了场景作依托,学习抽象的代数知识时能言之有物,使等量关系的表达更清晰、简洁.
学生从用数字符号,到用图形,最后到用字母符号表示生活中的等量关系,这过程是学生算术思维向代数思维发展的一个飞跃.需注意的是,“符号化”是“代数思维”的主要特征,但并不是它的本质,它的本质是对代数关系与结构的理解.因此,在教学中,教师要鼓励学生多用自己的方式表达,不宜过早教给学生正式的代数形式.
四、结 语
学生代数思维的形成必须经历数与代数的抽象、运算与建模等结构转换,才能实现质变的过程.教师要做到有大观念,充分挖掘,有序渗透,实现数与代数由“操作性观念”向“结构性观念”的转变,为后续学习打下基础.
【参考文献】
[1]章勤琼.小学阶段“早期代数思维”的内涵及教学[J].小学教学数学版,2016(11):10-13.
[2]鄭毓信.数学教学与学会思维——“教数学、想数学、学数学”系列之四[J].小学数学教师,2015(6):4-11.

