展现数学思维 培养创新能力

姬振宁

摘要：新课程标准要求从实践出发，以学生为本，培养学生运用所学知识解决实际问题的能力。在数学教学中，让数学创造进入课堂，激发学生数学创新思维的动机，展现数学思维过程，引导学生探索数学创新的规律，实施开放式数学教学，将有助于培养学生的创新思维。一、创设问题情境，培养思维的探求性古人说："学起于思，思起于疑。""读书无疑者，须教有疑;有疑者却要无疑，到这里是长进。"从无疑到有疑，是提出问题的过程。

关键词：数学教学;创新思维能力;培养途径

前言：

未来社会的数学素养在创造能力方面至少做到：能通过解决日常生活中的实际问题，发展、提炼数学模型，了解数学方法，注意数学应用的创造能力，并形成坚定、自信、坚韧不拔的意志品质，随着科学技术的迅猛发展和培养人才的需要，现代数学教育越来越重视学生思维创造能力的培养。任何一科学创造能力都可以用如下的公式估计：

一、创造能力=知识量×思维能力

并进一步强调指出：“数学上的新思想、新概念和新方法往往来源于各种有趣的思维。”因此，重视展现学生思维，是培养学生创新能力的重要环节。

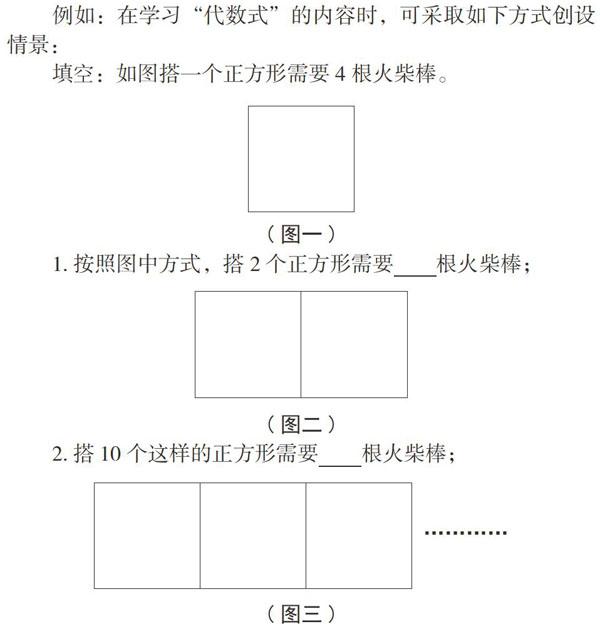
例如：在学习“代数式”的内容时，可采取如下方式创设情景：

填空：如图搭一个正方形需要4根火柴棒。

1.按照图中方式，搭2个正方形需要______根火柴棒;

2.搭10个这样的正方形需要______ 根火柴棒;

…………

3.如果用X表示所搭正方形的个数，那么搭X个正方形需要       根火柴棒，与同伴交流。

显然，在这样的学习情景中，学生是以“做”而非“听”或“看”的方式介入学习活动，而且是实实在在地进行观察、实验猜测、验证推理与交流等学习活动。

二、探究尝试 寻求结论

这一环节最重要的是充分发挥学生的主动性、思维开放性。学生在教师创设的数学情景中获得求知、探索的欲望，很自然地会运用已有的知识经验，用自己的思维方式去探索，去发现。例如在前面提到的问题情景中，搭2个、3个、10个正方形时，学生们可能会数一数火柴棒的根数，但是当搭100个正方形时，学生们就需要探索正方形个数与火柴棒的根数之间的关系，发现火柴棒根数的变化规律，规律是一般性的，需要用字母表示，用x表示正方形的个数来提示规律，在认识上是一次飞跃，学生们完成这次飞跃无疑需要时间思考，不能急于求成，不能怕完不成既定的教学任务而压缩学生们独立思考的时间，也不能用所谓的“规范”或“标准答案”扼杀学生的积极性和创造性。

三、合作交流

教学是一种社会性认识活动，交流对学生有着重要的发展价值。首先，交流活动具有生成性，与别人即时即景的交流，往往会启发自己的思维;学生通过小组讨论交流、班级反馈交流等各种形式的学习交往活动，可以学会理清和表达自己的见解，学会聆听和理解别人的看法，促使他们不断对自己的观点进行反思，从而活跃他们的思维，拓宽他们的思路，激发他们的创新热情。其次，学生们在小组合作交流中，由班级中几十分之一变成几分一次，大大提升了学生的参与度，货到较多的展示自己的机会，学习的积极性空前提高。第三，交流还有利于培养学生的合作意识和合作技能等社会性品质，并且可以使学生回顾、审查自己探究过程和方法，总结经验和教训，改进学习方法，学会学习。

四、运用评价，促进全体学生的共同发展

探究发现教学模式虽然从教学环节上给每个学生的发展提供了平台，但是受学生个性差异及各种因素的影响，学生参与活动的程度不尽相同。教学中应避免将探究活动变成少数学生的舞台，使“弱势群体”得不到应有的发展机会，实践证明，建立健全一整套学生评价制度，通过学生成长记录这一形成性评价机制，可以很好的促进全体学生的共同发展，学生在探究活动中的出色表现、动手制作的作品、获得的各种奖励，教师和小组成员的相互评价等都可以作为整体评价的一部分。

新一轮课程改革强调教学过程是师生交往、共同发展的互动过程，在教学过程中怎样处理好传授知识和培养能力的关系？如何培养学生的独立性和自主性？如何引导学生质疑、调查、探究、在实践中学习？如何关注个体差异，满足不同需要？如何创设能引导学生主动参与的教育环境，激发学生的学习积极性，培养学生掌握和运用知识的态度和能力，是每个学生都得到充分的发展？探究发现教学模式对这一系列的问题进行了有益的探索和尝试。

参考文献：

[1]朱成枫.创设多种教学情境 培养学生创新思维[J].教育艺术，2009 （04）：17-19.

[2]培养数学创新能力 推进素质教育[J].胡惠婵.太原教育学院学报.2001 （01）

[3]试谈培养学生数学创新思维的几种途径[J].郁明.新課程研究（基础教育）.2007 （10）