基于空间效应的弃渣场边坡稳定性方法探讨

孙朝燚 ，陈从新 ，郑 允 ，鲁祖德 ，邓洋洋

（1. 中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，湖北 武汉 430071；2. 中国科学院大学，北京 100049）

随着国家经济的发展，各种电厂、公路等基础设施的建设也不断增加，这些施工建设过程中常常涉及挖方填方工程，扰动原始地貌，并积累大量弃土弃渣. 弃渣场址的选择和堆置高度必须符合水土保持技术规范设计[1]，满足水土流失防治的原则和弃渣场边坡的稳定安全[2-4].

目前针对边坡的稳定分析和安全评估已有较多研究成果，基于空间效应的三维边坡稳定性更是研究的热点. 所谓空间效应是指坡面的凹凸形态、滑体的端部效应以及坡体的走向对边坡稳定性的影响.朱乃龙等[5]通过深凹露天矿岩质边坡的研究，提出了深凹岩质边坡稳定角的理论公式；汪海滨等[6]依据现场工程、理论分析和模型模拟证实了凹形坡面的空间夹持效应和凸形坡面的发散作用，建立了边坡进行二维和三维稳定性分析所应遵循的高度和曲率半径之间的关系；卢坤林等[7]从统计、试验和理论3方面研究了坡面凹凸形态对边坡稳定的影响，并制作了不同坡面形态的边坡安全系数速查曲线以供工程应用；Rassam等[8]通过矿山废石堆坡面形态的研究，表明凹形边坡极限稳定角至少要比直线边坡大 2°，凸形边坡的极限稳定角要比直线边坡小0.5°；卢坤林等[9]针对二维和三维边坡安全系数存在的差异，定性讨论了长高比、坡度和土体参数对稳定性的影响，得出滑体端部效应造成安全系数本质差异的结论.

上述研究成果都是围绕坡面的凹凸形态和滑体的端部效应对边坡稳定性影响的研究，关于坡体的走向对边坡稳定性影响的相关文献很少，更鲜见走向夹角对弃渣场边坡稳定性影响的研究. 因此，本文基于弃渣场走向存在夹角的几何形态特征进行分区研究，通过数值模拟分析弃渣场走向有无夹角对潜在破坏机制的影响，结合走向为折线形的弃渣场潜在破坏机制的理论探讨，提出了考虑走向夹角因素的不平衡推力法，并展开边坡稳定因素的敏感性讨论，为类似折线形走向边坡的稳定性分析和治理设计提供参考意义.

1 工程概况

某核电厂弃渣场场址位于一个冲沟内，如图1，图中，ZX1、ZX2和ZX3表示3个钻孔编号. 冲沟全长约为 350 m，走向约为北东 50°，在截面上呈“V”形. 冲沟起点高程约为100 m，冲沟终点高程约为2 m，高差约为98 m，总体坡度约为16°，较为平缓. 弃渣体的顶端面高程约为70 m，底端高程约为33 m. 弃渣体堆放于冲沟的中部，上部区域走向为62°，下部区域走向为34°，平面呈“折线”形，折线夹角28°. 弃渣体堆置长度约为160 m，堆置高度约为37 m，总体积约为2.94 × 104m3，呈纺锤体形态.

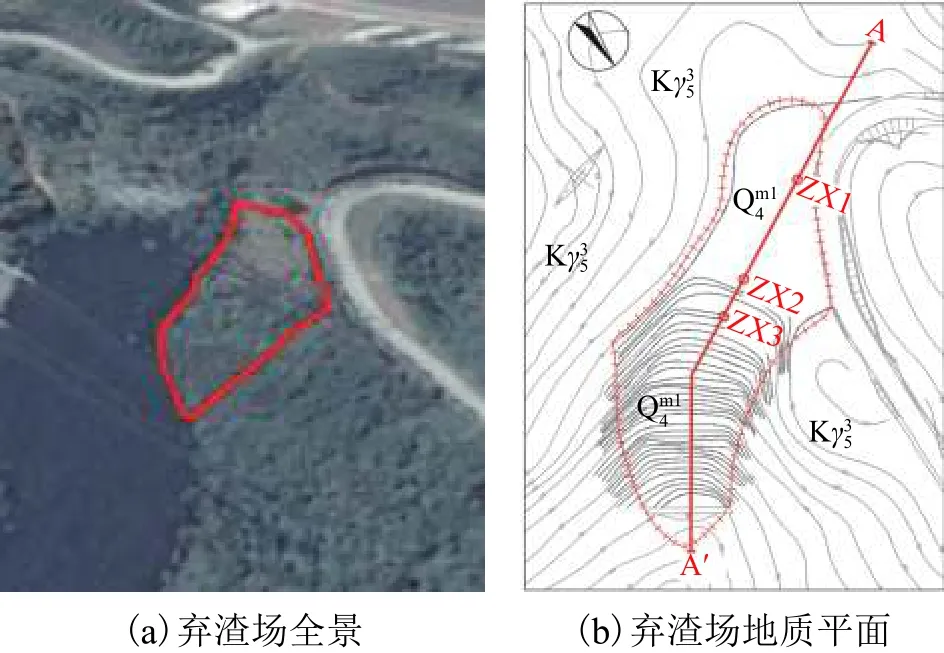
图1 弃渣场概貌Fig.1 General picture of abandoned dreg site

1.1 工程水文地质

弃渣体主要来源于核电厂施工进场道路改造项目的3段路堑边坡，主要由黑云母花岗岩（占总体积的80%）和粉土（占总体积的15%）组成.根据钻探揭露，整个弃渣场的岩土体可以划分为第四系堆填碎石土（弃渣体）、第四系残积层和侏罗系燕山期花岗岩层. 第四系人工堆填土为人工堆填的弃渣体，厚约6.4～13.2 m，呈杂色散体状，主要由块石、碎石、砂、黏性土等组成，其中块石、碎石、中砂等含量约90%，块石粒径约30～40 cm，碎石粒径约2～20 cm；第四系残积层岩性为粉质黏土，厚约1.4～2.3 m，呈浅灰色、灰黄色，饱和、可塑，局部可见残留的花岗岩结构；侏罗系燕山期花岗岩层岩性为中风化黑云母花岗岩，厚2.1～5.8 m，岩石风化较明显，锤击声较脆、不易击碎，节理裂隙较发育，岩芯呈柱状和碎块状.

弃渣体的堆填碎石土层透水性很强，属于强透水层，在正常运行状态下，水位很低，基本上处于下伏第四系残坡积粉质粘土层附近.

1.2 岩土体物理力学参数

为了准确评估弃渣场边坡的稳定性，通过分析勘察和试验结果，同时结合工程类比，并进行弃渣场岩土体粒径分析，综合确定了弃渣场岩土体物理力学参数，如表1所示. 其中：弃渣土和粉质黏土的计算参数主要是通过室内物理、力学试验和室外动力触探、标准贯入试验以及工程类比综合确定；中风化花岗岩参数主要按照《工程岩体分级标准》来确定，根据现场调查结果，中风化花岗岩属于Ⅲ级岩体，然后再通过查表C.0.1（《工程岩体分级标准》附录C）可确定花岗岩的基本参数[10].

表1 计算所采用的材料参数Tab.1 Material parameters used in analysis

2 数值模拟

弃渣场原始地貌属于低山丘陵，地形复杂，而且，弃渣体折线形走向，呈纺锤体形态，空间效应显著. FLAC3D专为岩土工程力学分析而开发，三维空间行为模拟准确可靠，通过内置强度折减法或自编强度折减法都能实现边坡安全系数的求解[11]. 鉴于此，本研究采用FLAC3D自编强度折减FISH语言计算弃渣场的安全系数，分析弃渣场的稳定性.

2.1 三维模型的构建

目前国内外优秀的三维建模及可视化的软件多不胜数，常见的有 GOCAD、ArcGIS、EarthVision、GemCom、Petrel、MineMap、Micromine等，已经广泛应用于岩土、石油和采矿等领域. 这些软件对模型可视化已相当卓越，但是由于各自研发平台的不同，在结合通用计算软件时却非常复杂[12-13]. 国内学者为此做了相应的研究：文献[13]基于AutoCAD平台，借助AutoLisp语言，采用滑动最小二乘法插值拟合的方式构建三维模型；文献[14]提出先以Sufer软件提取地质信息，再经自编FISH语言二次转换生成FLAC3D简单模型的思路.

综合上述三维模型的研究成果，本文通过Sufer软件对空间数据进行Kriging法插值，以及ANSYS软件对各地层进行布尔运算和网格划分，建立三维复杂数值模型，建模精度高且效率快. 具体方法：（1） 采用dxf2xyz软件将各等高线地形图的三维坐标一次性获取；（2） 通过Sufer软件对空间数据进行Kriging法稳定插值，得到有规律高精度排列的网格点坐标；（3） 利用Sufer-ANSYS转换接口，将网格点三维坐标导入ANSYS中，采用蒙皮技术形成各地形层面，通过布尔运算对各地层进行切割组合，然后对地质模型划分网格生成数值模型；（4） 通过ANSYS-FLAC3D转换接口，将数值模型导入FLAC3D软件进行计算.

根据本文三维建模的思路，选取弃渣场原始地形图和弃渣体堆积地形图，结合1.1节弃渣场的工程水文地质详述，得到FLAC3D计算模型（如图2所示）. 数值计算模型长250 m，宽150 m，高110 m，共有67 278个单元，13 645个节点.

图2 弃渣场FLAC3D模型Fig.2 FLAC3D model of abandoned dreg site

2.2 数值计算结果

该弃渣场模拟时主要使用节点速度约束条件，约束模型四周及底部的节点速度值. 模型顶面为自由边界，底面和两个侧面的3个方向位移设置为0.由于弃渣场的稳定性主要涉及到堆土体以及作为弃渣场基础的浅部岩土体的稳定性，因此计算中不考虑构造应力，仅考虑自重产生的初始应力场，首先对弃渣场模型采用弹性本构生成初始应力场，然后将模型的位移场和速度场置0，最后采用Mohr-Coulomb弹塑性本构和强度折减法进行弃渣场三维整体稳定性分析.

对边坡进行有限差分强度折减时，失稳判据对确定安全系数至关重要，目前常有如下3种[11]：（1）数值计算是否收敛；（2） 特征部位位移是否突变；（3） 塑性区是否贯通. 本文综合考虑采用最大位移区域的特征点（图2中坡脚位置所标注的位移特征点）是否位移突变及塑性区是否贯通作为判断标准.

结合该弃渣场的特点及工程水文地质条件，主要考虑自重工况下边坡的安全稳定. 图3分别显示了有无上部区域弃渣场模型的特征点位移曲线图，以及位移突变对应折减倍数下的塑性区变形图. 从图3（a）中可以看出，整体区域弃渣场在折减1.55倍数时，特征点位移曲线发生了突变，相应折减倍数下塑性变形区也贯穿了弃渣场（图3（b）），形成封闭的滑动体，因此弃渣场整体安全系数为1.55；同理根据图3（c）、（d）可判定上部弃渣场不存在时，弃渣场安全系数为1.70. 1.55 ＜ 1.70说明弃渣场的上部区域存在传递到下部区域的剩余下滑力，上部区域对下部区域存在挤压推动作用.

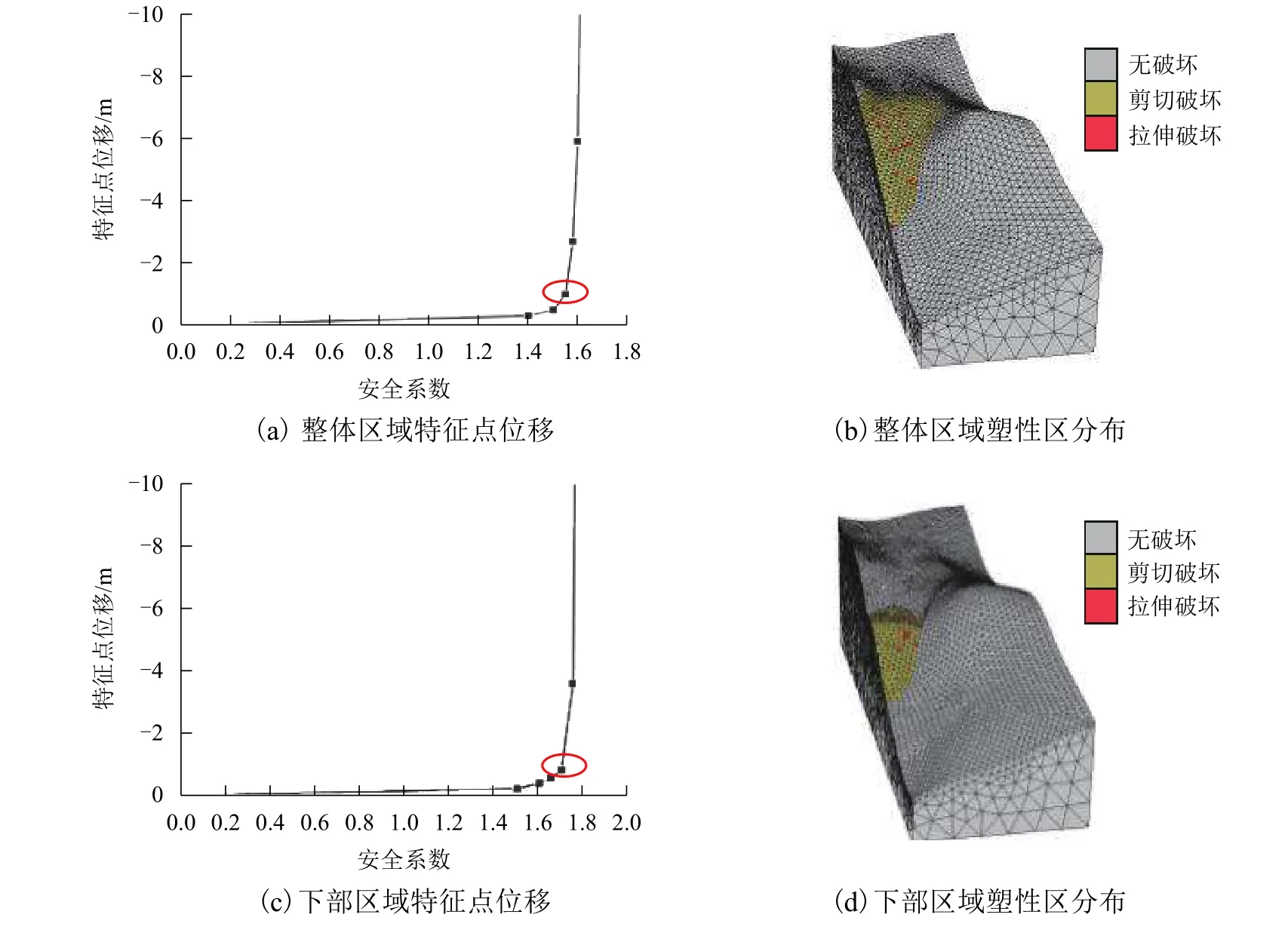
图3 弃渣场强度折减计算结果Fig.3 Calculation results of abandoned dreg site using SRM

2.3 潜在破坏机制分析

2.2 节从边坡稳定性方面已经说明该折线走向的弃渣场边坡上部区域对下部区域存在挤压推动作用，但是具体的传递机制尚不明确，本节将通过大主应力云图讨论弃渣场潜在破坏机制，分析走向夹角对剩余下滑力传递的影响，如图4. 图4（a）为该弃渣体强度折减后的大主应力云图（云图值显示为正值，即受拉状态），从图中大主应力的分布可以看出，下部弃渣场的大主应力沿轴线两侧并非对称分布，外侧区域大主应力值为负（受压状态），内侧区域为正（受拉状态）. 因弃渣场堆积体体积较小，现场调查和三维模型均表明其坡面为平面形态，弃渣体对称分布于轴线两侧，从坡面形态方面来说，弃渣体不易发生垂直于轴线方向滑动，形成不对称应力分布，造成该现象的主要原因是弃渣场走向存在夹角，上部区域的剩余下滑力只能沿轴线斜交作用于下部区域，不能完全传递至下部区域.

为了更好地解释分区作用机制，根据受力特点对弃渣场进行了更细的区域划分，如图4（b）所示（区域A为受拉区域，区域B为过渡区域，区域C为受压区域），图中，区域B上下边界的交点为弃渣场轴线内转折点，上边界垂直于区域A轴线，下边界垂直于区域C轴线. 区域A的拉应力超过抗拉强度时，发生主动土压力破坏，生成垂直于滑坡方向（坡体走向）的张拉裂缝，因走向夹角的原因造成张拉裂缝未垂直区域C轴线，即区域A剩余下滑力未沿区域C的走向作用，说明走向夹角使得区域A的剩余下滑力并未全部向下传递，区域B相当于过渡区域，将区域A的剩余下滑力分解传递至区域C.

图4（c）为直线走向的概化弃渣场模型，从其强度折减后的大主应力云图分析可知，走向夹角为0时，其大主应力云图沿轴线对称分布，则上部区域的剩余下滑力沿轴线方向作用，全部传递给下部区域.因此走向为折线的弃渣场相对走向为直线弃渣场的剩余下滑力传递能力更低，边坡稳定性更高.

图5为该弃渣场强度折减后的各剖面剪应变增量云图，图中，剖面位置沿箭头方向依次为x = 50，60，70，80，90，100，110，结合图 3（a）和图 4（a）中的塑性变形图和大主应力分布图可以深入分析其潜在破坏机制：弃渣土堆积的坡脚位置先发生大变形，而后粘土夹层发生塑性屈服流动，使得坡顶位置处形成拉裂缝，最终贯穿形成滑动带，发生滑移-拉裂破坏. 最可能失稳模式是沿着弃渣体内部和底部粉质粘土层的滑移-拉裂破坏.

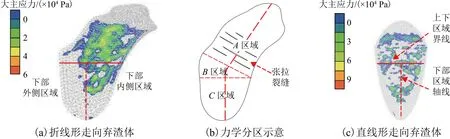
图4 强度折减大主应力云图Fig.4 Contour plot of major principal stress using SRM

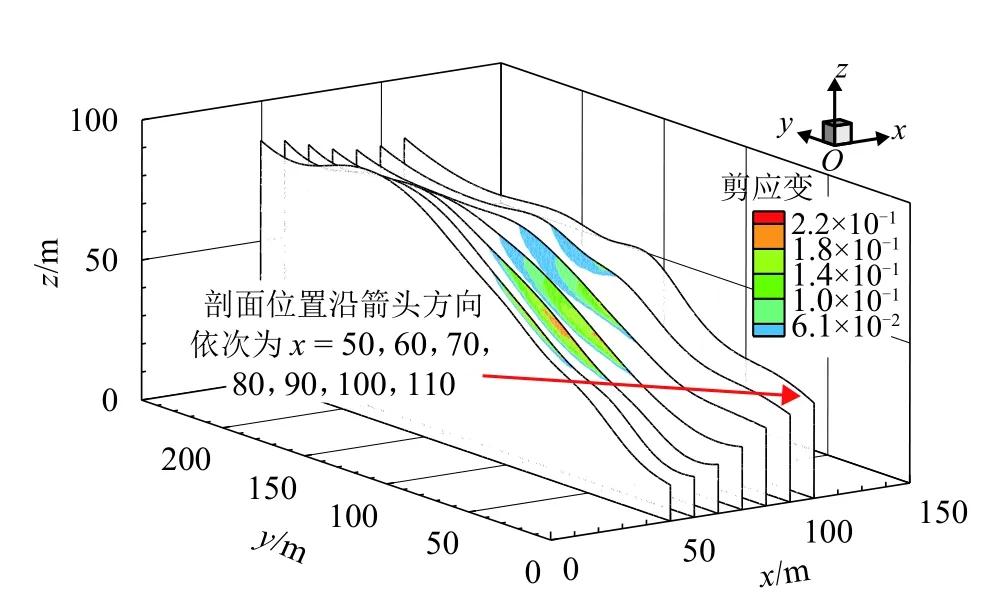
图5 各剖面剪应变增量云图Fig.5 Contour plot of shear strain increment for each section

3 理论探讨

本文针对该弃渣场的走向特点，通过几何形态分区的数值模拟证实了上部区域对下部区域存在剩余下滑力作用，而且上下区域的走向夹角影响着弃渣场的应力分布和力的传递，可是该上下区域弃渣场究竟是如何进行力的传递作用呢？为了从力学角度进一步分析上下区域弃渣场力的传递作用，更快速更准确地应用于类似工程，本节基于不平衡推力理论，提出了考虑走向夹角因素的不平衡推力法，并对其稳定性影响因素展开敏感性分析.

3.1 力学简化模型

根据图4（b）弃渣场的力学分区，采用静力学理论，将区域A、B定为①号条块，区域C定为②号条块. 两侧沟谷对区域A、C的支撑力为平衡力系，不影响条块的力学效应，因此只考虑区域B外侧沟谷支撑力 FR对条块的作用，得到图6所示的弃渣体受力示意图，图中： θ 为走向夹角； E1为①号条块的剩余下滑力； E2为②号条块的剩余下滑力； E12为①号条块传递至②号条块的剩余下滑力； E21为②号条块对①号条块的反作用力.

图6 弃渣体受力示意Fig.6 Force diagram of abandoned dreg body

对分离条块进行受力分析：

当 θ = 0° 时， E12=E1， FR=0 ，表明①号条块的剩余下滑力沿轴线全部传递至②号条块，退化为常见的直线走向弃渣场边坡稳定性分析.

当 θ = 90° 时， E12=0 ， FR=E1，此时①号条块的剩余下滑力全部与 FR相平衡，不能传递至②号条块. 实际中区域B因沟谷边界的阻挡作用，主要发生垂直于区域A走向的鼓丘变形，少量沿区域C走向的变形，因此区域A的剩余下滑力基本不会传递至区域C.

3.2 不平衡推力法

不平衡推力法基于滑裂面已知的情况下，假定条间力与上一条块底面平行，结合弃渣场渗透系数大、地下水位低的特点，笔者不考虑地下水的作用，得到图7所示的条块受力分析图.

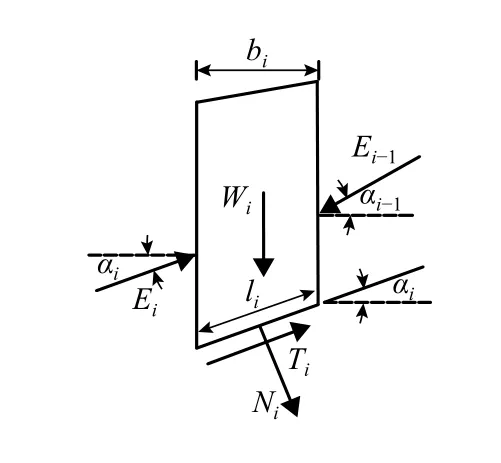
图7 条块受力示意Fig.7 Force diagram of slice

图中：

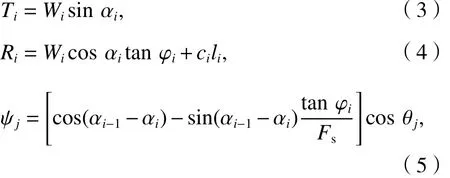
式中： i 为条块编号 i =1,2,··· ； Ei、 Ei-1分别为 i号和i-1号条块剩余下滑力，E0= 0； Ti为i号条块下滑力 ； Ri为 i号 条 块 抗 滑 力 ； ψj为 传 递 系 数 ，j=1,2,···,i-1 ； Wi为 i号条块重力； αi、 αi-1分别为i号和i-1号条块底倾角 , ao=0 ； φi为条块内摩擦角； ci为 i号条块粘聚力； li为i号条块底滑面长度； θj为 条块间走向夹角， θ1表示①号条块与②号条块之间的走向夹角，以此类推.

结合传统不平衡推力公式[15]，依据力的平衡，考虑式（1）的走向夹角影响因素，得到适用范围更广的不平衡推力法，即式（6）. 求解安全系数时，采用强度储备概念定义安全系数（即为弃渣场整体安全系数Fs，与各条块安全系数相等），先假定一个初始安全系数，然后从第1条块逐个向下推求，求出最后1个条块的剩余下滑力 En，直到 Fs满足 En= 0的要求.

3.3 理论分析结果

本文针对弃渣场数值计算结果，将塑性位移明显不连续处作为滑裂面. 首先对FLAC3D强度折减后的位移云图进行切片，寻找不连续位移所处位置，将切片上的位置点坐标导入ANSYS中，采用蒙皮技术生成滑裂面，通过布尔运算切割弃渣体，得出滑体范围，滑体体积和滑面面积可直接通过ANSYS软件获取. 为便于考虑走向夹角因素的不平衡推力法二维分析，笔者沿走向切割滑体生成滑体纵断面，通过ANSYS软件获取滑面面积和滑线长度，计算弃渣场纵断面上下区域的下滑力和抗滑力（表2）.

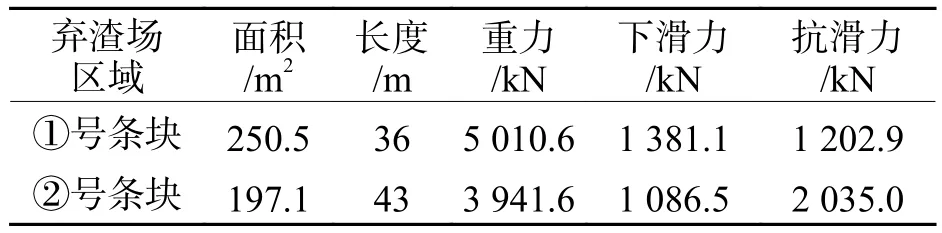
表2 滑体分区及其受力状态Tab.2 Region division and stress states of sliding mass

该弃渣场主滑面近似为一平面，可视为平面滑动，式（6）简化为 ψj=cos θj. 为便于进一步探讨分析弃渣场区域作用机制，简化条块划分，沿纵断面转折点分为上下两条块，即①号条块，②号条块，因此式（3）～（6）简化为

式中： E1=T1-R1/Fs，为①号条块的剩余下滑力.

通过式（1）和式（7）可计算①号条块传递到②号条块的剩余下滑力（ E12）和弃渣场整体安全系数（ Fs），如表3所示(，其中幅)度表示其它走向夹角相对 0° 的差异，即-/表示 E12降低幅度，-)/表示 Fs提升幅度，上标 0 指 θ1=0° 的情况， x 指 θ = x°的情况. 由表3可知： θ1对E12和 Fs影 响很大， E12随 θ1增大而减小， θ1= 90°时， E12降幅达 100%； Fs随 θ1的增大而增大， θ1=90° 时， Fs增幅达 40.8%. 针对该倾角为 16° 走向夹角为 28°的弃渣场， E12= 409.53 kN， E12降低了7.6%，传递能力为92.4%； Fs= 1.36， Fs增大了2.2%，说明 θ1增大有利于弃渣场边坡的稳定性，但是稳定性幅度提升并不明显.

表3 不同走向夹角的剩余下滑力和安全系数Tab.3 Residual sliding force and safety factor of different angle of strike

此外，该弃渣场采用考虑走向夹角因素的不平衡推力法进行理论计算所得的 Fs= 1.36，与数值模拟强度折减结果1.55十分接近，两者相差约12%.

3.4 数值模拟与理论计算的比较

为了进一步展开数值模拟与理论计算的比较，验证数值模拟和理论计算结果的准确性，本节补充了坡体走向夹角为 0°、30° 和 60°3个边坡数值模型，如图8所示. 模型中冲沟坡度为16°，走向夹角为 0°、30° 和 60°，冲沟内堆填了上下两个区域的弃渣，下部区域堆积的弃渣长度均为105 m、体积均为41 365 m3，上部区域堆积的弃渣长度近似为90 m、体积近似为45 000 m3. 冲沟内上下区域的弃渣强度参数不同，上部区域弃渣的强度参数小于下部区域，以突出上部区域对下部区域的传力挤压作用，具体参数见表4. 通过2.2节的数值分析方法和3.3节的理论分析方法对3个边坡模型展开稳定性研究，结果如表5所示.

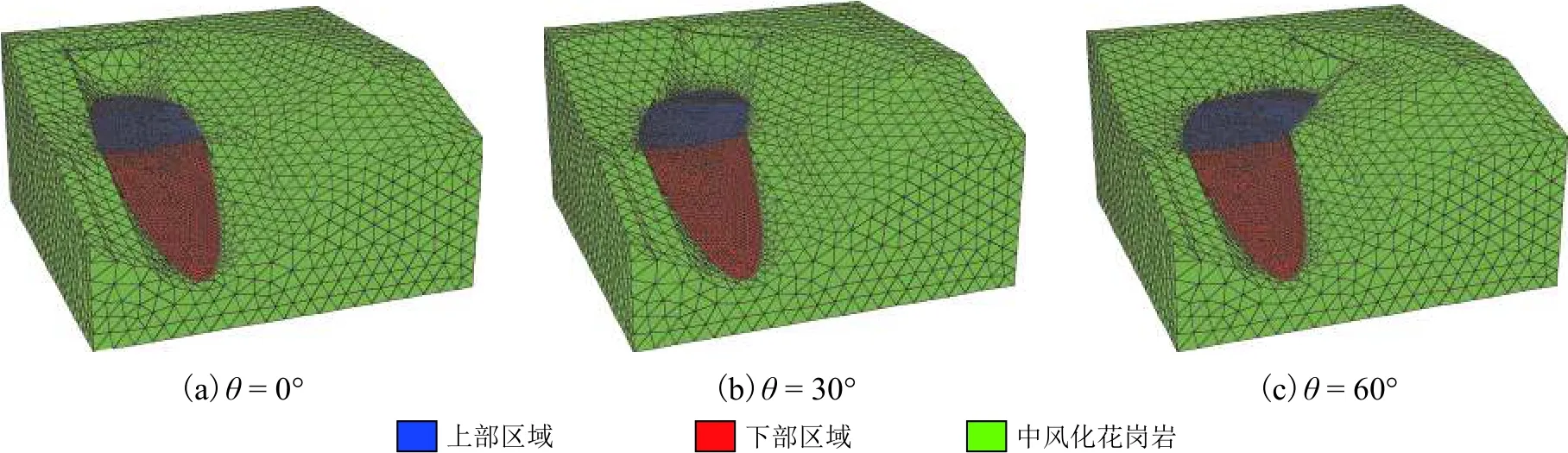
图8 不同走向夹角的边坡数值模型Fig.8 Slope numerical models for different angle of slope strike

表4 数值分析所采用的材料参数Tab.4 Material parameters used in numerical analysis

表5 数值模拟和理论计算的比较Tab.5 Comparison of numerical simulation and theoretical calculation

由表5可知，不同走向夹角边坡的数值模拟和理论计算的结果十分接近. 走向夹角为0° 时，两者计算所得安全系数相差5.80%；走向夹角为30° 时，两者计算所得安全系数相差5.76%；走向夹角为60°时，两者计算所得安全系数相差7.69%. 虽然数值模拟和理论计算所得结果存在一定差异，但总体来讲，两者结果较为一致，能够相互验证. 此外，表中边坡安全系数 Fs随 走向夹角 θ 的增大呈升高趋势，但是从安全系数提升幅度来看并不明显.

3.5 稳定性因素敏感性分析

针对3.3节和3.4节所得边坡安全系数 Fs随走向夹角 θ 增大而升高，但是提升幅度并不明显的结果，本节进一步展开该弃渣场稳定性因素的敏感性讨论. 考虑①、②号条块走向夹角 θ1和倾角 αi（i =1，2）的变化，式（7）变形为式（8），分别取 θ1= 0°，28°，60°，90°， αi= 10°，16°，25°，采用 MATLAB 编程迭代求解 Fs，进行弃渣场稳定的敏感性讨论. 图9给出了 Fs随 θ1的变化曲线，整体上看： Fs随 θ1的增大而提高，当 θ1＜ 60° 时， θ1每增加 10°， Fs平均提高 0.03；当 θ1＞ 60° 时， θ1每增加 10°， Fs平均提高0.23. 故当 θ1＞ 60° 时 Fs提升幅度明显，此时不能忽 略 θ1的空间效应对边坡稳定性的影响.

图9 不同走向夹角的边坡数值模型Fig.9 Slope numerical models for different angle of slope strike

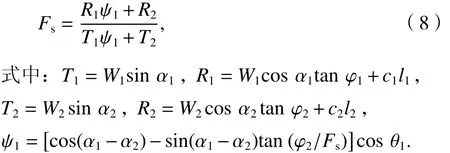
具体来看，图9（a）表明，①、②号条块倾角相同时，随着 αi增 大 Fs减小，但 Fs提升幅度随 αi增大而降低. 该结论可从数学计算方面考虑分析，随 αi增大， Ti增 大 Ri减 小，则 Fs减 小且 E1增 大，但是 E1增值相对 T2增值并不明显， θ1的变化相对式（7）分母变化的影响较小. 即②号条块 T2和 R2变化对 Fs的影响超过了①号条块传递到②号条块的 E12影响，则 α1=α2时，随 αi增 大， θ1对 Fs影 响逐渐减小，Fs提升幅度降低.

图 9（b）表明，②号条块倾角 α2= 16° 时，①号条块倾角越大， Fs提升幅度越高. 这是因为②号条块受力不变的情况下，①号条块越陡， E1越大，传递到②号条块的 E12受 θ1影响更明显，则随 α1增大， θ1对 Fs影 响逐渐增大， Fs提升幅度升高.

图 9（c）表明，①号条块倾角 α1= 16° 时，②号条块倾角越大， Fs提升幅度越低. 这进一步说明α2增大后，②号条块 T2和 R2变化对 Fs的影响超过了①号条块传递到②号条块的 E12影响，即随 α2增大，θ1对 Fs影响逐渐减小， Fs提升幅度降低.

当 α1=10°， α2=25°， θ1=0°时，边坡 Fs= 1.19.单独分析①号条块的 Fs= 1.46，单独分析②号条块的 Fs= 1.19，此时①号条块比②号条块稳定，并没有向下作用的 E1， 即 θ1对边坡的稳定性没有影响.由此说明 θ1对边坡稳定性的影响主要取决于上部区域（①号条块）向下传递的 E1大小，故对于后推式滑坡， θ1的空间效应对边坡稳定性影响更为显著.

4 结 论

（1） 走向夹角对弃渣场边坡力的传递和安全系数有着重要的影响，走向夹角越大 Fs越大. 当走向夹角大于60° 时， Fs提升幅度明显提高，此时不能忽略走向夹角因素对边坡稳定性的影响.

（2） 边坡坡脚区域（②号条块）倾角越小，坡顶区域（①号条块）倾角越大时， θ1对 Fs影响较大. 后推式滑坡， θ1的空间效应对边坡稳定性影响更为显著.

（3） 走向为折线的弃渣场相对走向为直线的弃渣场来说，其下部边坡区域的应力场分布呈非对称形式. 走向夹角影响上部区域剩余下滑力向下传递的能力.

（4） 提出了通过 Kriging法插值空间数据及ANSYS软件连线蒙皮、布尔运算和网格划分的快速准确三维建模方法，实现与FLAC3D岩土计算软件无缝融合.

致谢：中国科学院青年创新促进会（2015271）的资助.