数字单周期电流控制在电磁悬浮系统中的应用

蒋启龙 ，梁 达 ,2，阎 枫

（1. 西南交通大学电气工程学院，四川 成都 611756；2. 磁浮技术与磁浮列车教育部重点实验室，四川 成都611756）

电磁吸力悬浮系统具有非线性、不自稳的特点，为达到稳定悬浮的目的，一般采用气隙-电流双环控制，其中气隙外环根据气隙指令和实际气隙通过一定控制律获得电流指令信号；电流内环依据电流指令信号调节电磁铁线圈中电流，进而改变电磁吸力大小，最终实现系统稳定悬浮[1]. 电磁铁线圈属于大感性负载，会限制电流响应速度和跟随精度，从而影响到系统悬浮效果[2]. 电流环的作用就是让线圈电流快速、准确地跟随指令电流信号.

为满足悬浮系统要求，电流环应具备以下特点：（1） 在噪声限制允许的范围内，电磁铁电流能够快速、精确地跟随指令电流[3]；（2） 有较强的鲁棒特性，以增强系统的抗扰动性能[4]；（3） 电流纹波应尽可能小，以避免悬浮力波动[5]. 在现存的电流控制中，基于bang-bang控制原理的电流环时间最优控制具有跟踪速度快的优点，但误差带较大，系统在受到随机扰动时极易失稳；次速电流控制结合了最速电流控制和PI控制的优势，电流调整速度与最速电流控制相当，且克服了最速电流控制抗干扰性能差的缺点[6]，但存在参数不易整定及控制状态切换点难以选择的不足，且达到稳态时会存在一定的跟随误差.为了改善电流响应性能，程金路等[7]和张东升等[8]分别采用有限拍算法和三步电流控制法来加速电流响应，但都存在计算复杂的缺点.

数字单周期控制理论是20世纪90年代初提出的一种非线性大信号PWM （pulse width modulation）控制理论[9]，其基本控制思想是保证每一个开关周期中开关变量与控制参考量相等或成比例. 该方法被广泛运用在电压型控制AC-DC和DC-DC功率变换器的控制中，且主要通过模拟电路来实现[10-11].由于单周期控制存在实现简单、鲁棒性强的优点，近年来有学者致力于单周期控制方法的数字化实现[12-16]. 文献[17-18]基于对一个开关周期电流波形高速多次采样，构建了数字形式的积分器来实现数字单周期控制（digital one-cycle control，D-OCC）；文献[19]在一个开关周期内对电流采样一次，并假设该开关期间电流为常数，忽略了开关周期内电感电流的变化，对系统瞬态性能的影响. 上述内容中，D-OCC方法都是在AC-DC电路中实现的，对此文献[20]提出将单周期算法应用于悬浮系统DC-DC功放电路控制中，实现了对指令电流的跟踪，但未与其他控制方法的跟随效果进行比较，也未在实际系统中验证是否满足悬浮系统的性能要求. 本文基于TMS320F28335 设计了EMS （electromagnetic suspension system）的D-OCC电流控制器，并将之应用到在实际悬浮系统的电流控制中进行悬浮实验. 实验结果表明，与电流环PID （proportion integration differentiation）控制相比，采用D-OCC具有更加平稳的动态响应性能.

1 悬浮系统及斩波器模型

EMS的反馈线性化模型如式（1）所示[21].

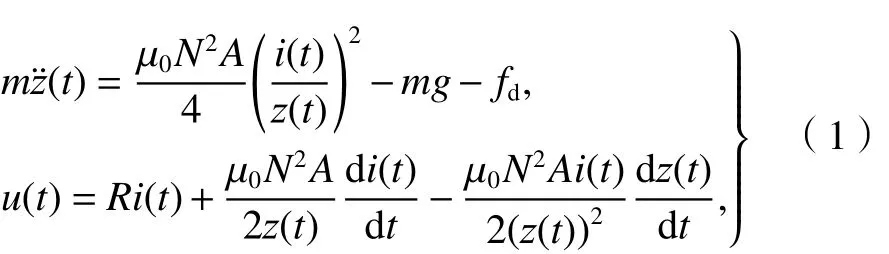
式中：i（t）为电磁铁线圈电流大小；z（t）为悬浮气隙；g为重力加速度；u（t）为电磁铁线圈两端电压；μ0为真空磁导率；m为电磁铁等效荷载；N为电磁铁线圈匝数；A为有效磁极面积；R为线圈内阻；fd为外力扰动.

根据式（1）给出的数学模型，可得EMS的气隙-电流双环控制结构如图1所示[22]，其中：z0为初始悬浮气隙；iref为电流指令.

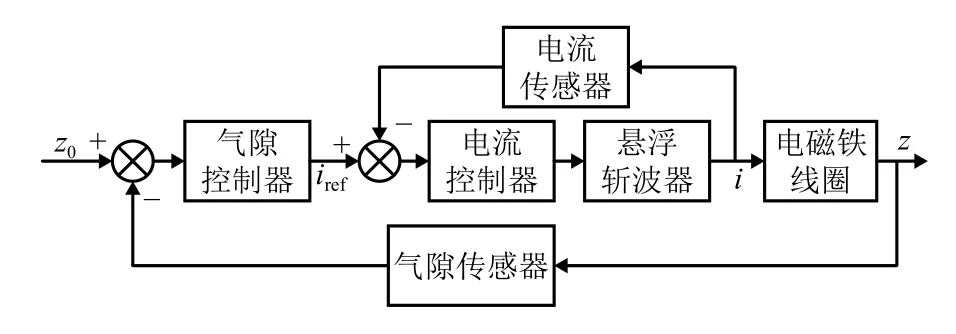
图1 悬浮系统气隙-电流双环控制结构Fig.1 Air gap-current double loop control structure of EMS

图1 所示控制系统结构的电流环部分传统方法采用PID控制，本文则采用D-OCC. 结合斩波器电路，该部分具体结构如图2所示，其中，Vgs1和Vgs2为驱动脉冲.

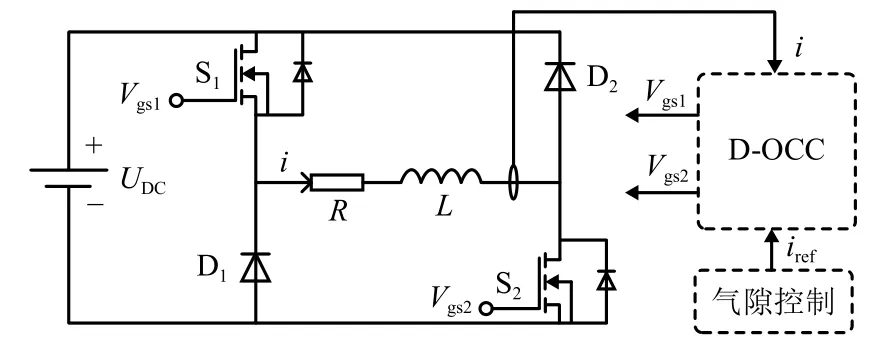
图2 悬浮斩波器电路及D-OCC原理示意Fig.2 Schematic diagram of chopper circuit and D-OCC

为了进一步研究D-OCC算法，首先对斩波器工作原理进行分析. 为达到电流快速调节的目的，斩波器一般采用S1、S2同时通断的控制方式. 由于悬浮系统稳定工作时线圈电流连续，且当S1、S2同时导通时，负载两端承受正向电压，电源给负载提供能量，线圈电流增加；当S1、S2同时关断，负载两端承受反向电压，能量从负载回馈至电源，线圈电流减小. 因此斩波器的数学模型可用式（2）进行描述.

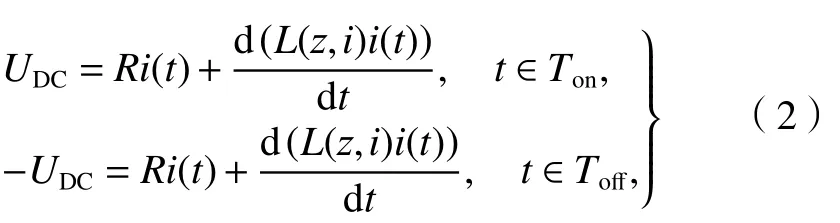
式中：UDC为直流母线电压；L为电磁铁的线圈等效电感.

假设悬浮电磁铁在额定点（z0，i0）邻域工作，悬浮气隙微小的变化对线圈电感、电阻的影响可以忽略；开关频率较快，且电磁铁线圈电感足够大，在一个开关周期内电感电流可以认为是线性变化的，则斩波器的数学模型简化为式（3）.

式中：R0、L0分别为电磁铁线圈在额定工作点的等效电阻和等效电感；iav为被采样开关周期的平均电流；Δi+、Δi-分别为对应周期内开关导通期间和关断期间线圈电流的变化量；Ts为开关周期；d为开关占空比.

悬浮线圈中电阻的存在限制了斩波器输出电流的大小，从而也就决定了系统在额定工作点的电流必须满足式（4）.

当线圈电流达到i0并维持恒定时，要求一个开关周期内开关导通期间电流增加量与断开期间电流减小量相等，则此时占空比如式（5）所示.

式中：d0为系统处于额定工作点时维持电流恒为i0所需的开关占空比.

由式（5）可知，维持恒定电流的占空比与电流大小呈现一次线性关系，斜率大小为 R /(2UDC) ，所需占空比随着电流增加而增大.

2 电流D-OCC原理

D-OCC的基本思想就是通过计算并给定开关占空比，使得采样开关周期内满足 iav=iref.

以一个开关周期为研究阶段，则在悬浮线圈工作过程中存在电流增加、电流平衡和电流减小3种状态. 设电流在第n开关周期变化量为Δi（n），则在电流增加状态 ∆ i(n)＞0 ， 电流平衡状态 ∆ i(n)=0 ，电流减小状态 ∆ i(n)＜0 .

以TMS320F28335为控制器，当采用增-减计数模式PWM波作为开关驱动时，3种电流状态的DOCC 波形分别如图 3（a）～（c）所示.

图3中：TBPRD和TBPHS分别为数字处理器时基周期寄存器和时基相位寄存器的值；ik为时刻tk线圈电流大小；Δik为时间段tk～tk+1内电流增量；ΔI为一个开关周期电流增量.

以电流增加状态为例进行分析. 电流增加状态的控制波形如图3（a）所示，第n开关周期电流变化量 Δi（n） ＞ 0，而每个开关周期又可以根据电流变化方向分为3个不同时间段：

（1） 时间段 t1～t2

在时间段 t1～t2，S1、S2同时导通，D1、D2关断，负载承受正向电压，线圈电流增大，由式（3）得电流增量方程为

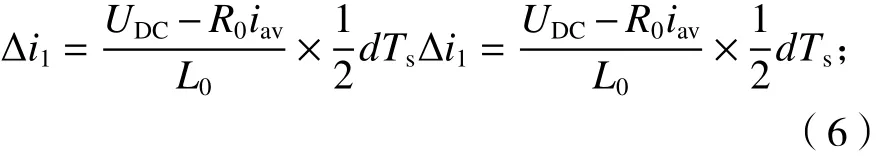
（2） 时间段 t2～t3

在时间段 t2～t3，S1、S2同时关断，D1、D2导通，负载承受反向电压，线圈电流减小，电流增量方程为

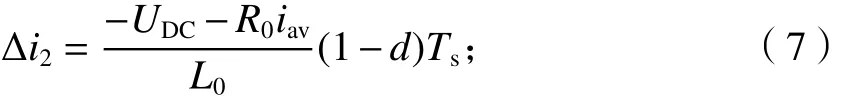
（3） 时间段 t3～t4

时间段t3～t4与时间段t1～t2类似，电流增量方程为

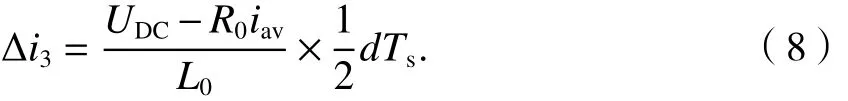
因此可得在增减计数PWM模式下，开关周期内电感电流的增量方程为

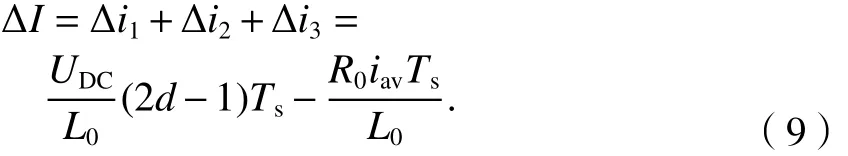
由式（9）可以推导出，该开关周期的开关占空比为

在采用图3给出的PWM控制波形情况下，周期内平均电流iav如式（11）所示.

图3 不同电流状态增-减计数PWM模式D-OCC波形Fig.3 Waveform of D-OCC based on up-down count PWM mode in different current states

根据D-OCC思想 iav=iref，可以得到：

将式（12）代入式（10），可得到最终占空比如式（13）.

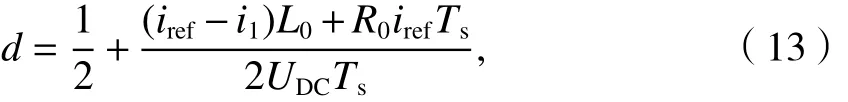
式中：i1为周期初始电流.

由式（13）可知，在恒压供电的方式下，每个周期只需要采样周期电流初值与参考电流大小即可计算出开关占空比大小，而悬浮系统中参考电流由气隙控制器给定.

上述给出D-OCC算法中开关占空比的计算过程. 对比式（6）和式（7）可知，开关导通时线圈电流增加速率小于开关关断时电流减小速率，且两者之间的差值随着平均电流的增加而增大. 因此，对初始电流为0的线圈负载施加满足式（5）所示占空比的PWM驱动波形时，线圈电流将以先快后慢的速率增加，当电流均值达到i0时，每个开关周期的电流增量为0 （单个周期开关开通期间电流增加量与关断期间电流减小量相等）.

3 单周期电流控制仿真及实验

为验证单周期电流控制算法的有效性，利用Simulink软件进行仿真验证，并对电流环D-OCC的悬浮模型与电流环PID控制的悬浮系统进行仿真和实验比较.

3.1 仿真及实验参数

磁浮小车的单电磁铁模型参数如表1所示.

表1 单电磁铁模型参数Tab.1 Single electromagnet model parameters

为使仿真结果与实际系统相对应，D-OCC算法仿真参数依据实际系统设定，具体参数如表2所示.

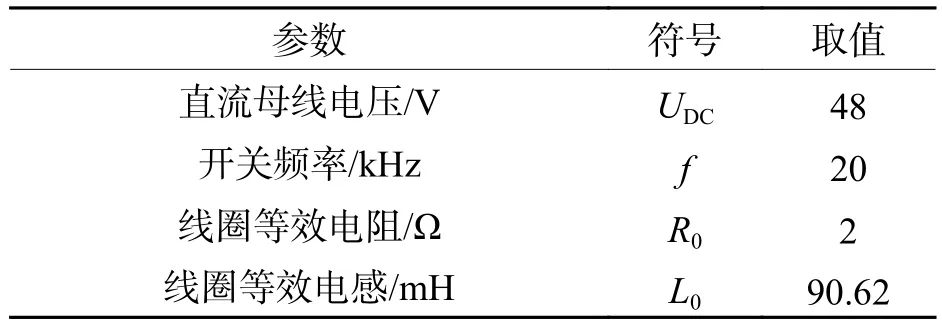
表2 仿真参数Tab.2 Simulation parameters

表2中：线圈等效电阻通过离线测量所得，线圈等效电感则根据公式 L0=µ0N2A/(2z0) 计算得出.

3.2 仿真及实验参数

根据表2给出的参数建立D-OCC的电流环仿真模型，对偏置为3 A，幅值为3 A，频率为5 Hz的方波指令电流进行跟随的仿真波形如图4所示. 由图4可知，D-OCC和PID控制下电流都可以快速跟随指令电流，电流稳定时两种控制方式的纹波幅值均为5 mA，但无论如何调节参数，PID控制始终存在不小于20 mA的稳态误差，且随着指令电流值的增加，稳态误差有增大趋势. 而在相同条件下，D-OCC则可以精确跟随指令值，不存在稳态误差. 仿真结果表明，对指令电流跟随效果的动态性能和稳态性能，D-OCC均满足悬浮系统要求.

图4 D-OCC电流跟随仿真波形Fig.4 Current follow simulation waveform based on D-OCC

将D-OCC算法应用到悬浮系统的电流环控制中进行仿真，系统启动、加减载及气隙扰动工况的仿真结果如图5和图6所示.

图5 数字单周期电流控制悬浮系统起浮及加减载仿真波形Fig.5 Simulation waveforms of levitation system using current D-OCC with conditions of no-load floating，50% loading and load shedding

图5 给出单周期电流控制悬浮系统起浮及加减载时电流和气隙波形. 由图5可知，电磁铁初始气隙为13.0 mm，起浮时最大电流达到12.0 A，经过0.25 s调整系统稳定悬浮在指定气隙6.5 mm的位置，电流稳定在3.0 A. 仿真运行至1.00 s时刻，系统加载3.25 kg，相当于空载质量的50%，电流迅速增加，峰值达5.0 A，悬浮气隙在增大方向上产生1.5 mm波动，经过约0.20 s的调整，电流减小并稳定在3.8 A，悬浮气隙恢复至6.5 mm. 仿真运行至2.00 s时刻，系统减载3.25 kg，电流迅速减小，悬浮气隙在减小方向上产生1.5 mm波动，经过约0.20 s的调整，电流增加并稳定在3.0 A，悬浮气隙恢复至6.5 mm.

图6 数字单周期电流控制悬浮系统气隙扰动仿真波形Fig.6 Simulation waveform of air gap disturbance condition in levitation system using current D-OCC

图6 给出单周期电流控制悬浮系统气隙扰动的仿真波形. 系统初态稳定在6.5 mm处，稳定电流为3.0 A，仿真运行至0.50 s和1.50 s时刻分别施加幅值为1.0 mm，持续15 ms的气隙扰动. 波形显示施加脉冲扰动瞬间电流和气隙都出现明显波动，但经过约0.20 s的调整系统重新恢复稳定状态.

仿真结果表明，采用D-OCC的电流环应用到悬浮系统中，可以实现系统稳定悬浮，并且有良好的抗负载扰动和抗气隙扰动性能.

为了进一步比较电流环分别采用两种控制方式时悬浮系统的控制性能，在气隙外环采用PID控制的前提下，电流内环分别采用PID控制和D-OCC进行仿真.

图7给出了两种控制方式在空载起浮和50%加载、减载情况下悬浮气隙的仿真波形. 由图7可知，无论是空载起浮、50%加载、50%减载工况，电流环采用PID控制的调节速度比采用D-OCC略快，但调节过程中气隙波动较大. 图8给出两种控制方式在稳定悬浮情况下受到1.0 mm气隙扰动时的气隙仿真波形，由图8可知，PID控制对气隙扰动较为灵敏，可以迅速作出响应，大约经过0.20 s可以调整恢复至稳态，但调整过程中出现3次气隙波动. 在相同气隙扰动条件下，D-OCC的响应情况较迟钝，但系统恢复至稳定状态的时间基本与PID控制相同，且调整过程中气隙波动次数较少，只出现1次波动. 当系统调节达到稳定状态后，两种方法对系统的控制效果基本相同.

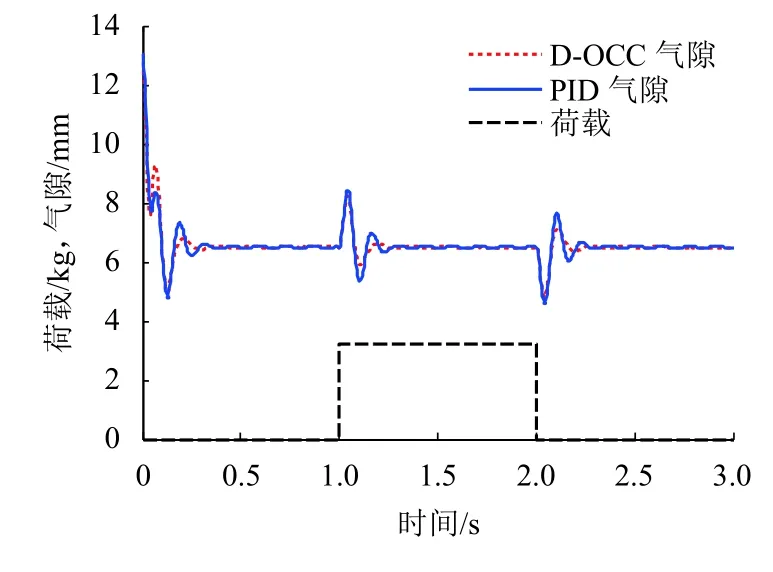
图7 两种控制方式空载起浮及50%加减载气隙波形比较Fig.7 Comparison of air gap waveforms in two control modes with conditions of no-load floating，50% loading and load shedding

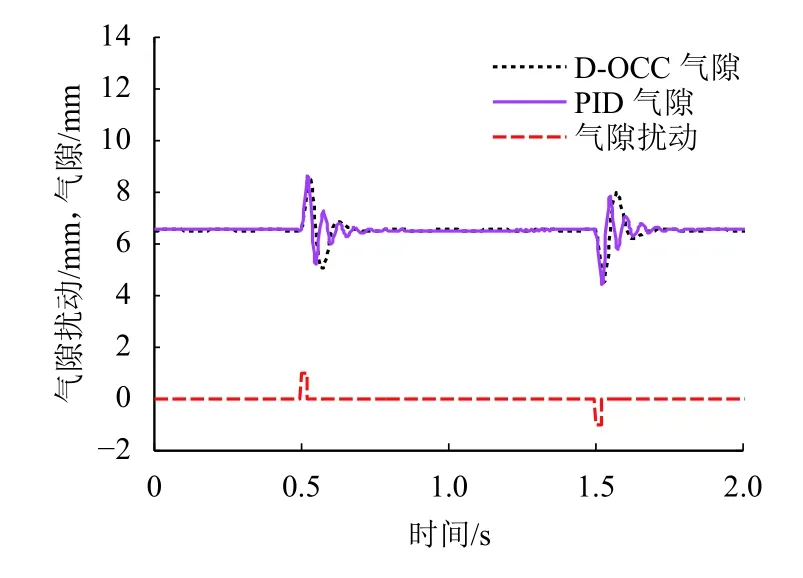
图8 两种控制方式1 mm气隙扰动时气隙波形比较Fig.8 Comparison of air gap waveforms in two control modes with1mm air gap disturbance

3.3 实验结果及分析

为了进一步验证D-OCC算法的有效性，设计基于TMS320F28335的数字单周期电流控制器，并将之投入到实际系统中进行悬浮实验.

悬浮小车单电磁铁模型机械结构如图9所示，图中：①表示电磁铁线圈，由500匝直径为1.62 mm的漆包线绕制而成；②是由铝合金材料加工成的连接板，用于实现悬浮电磁铁与悬浮架之间的刚性连接；③是采用电工纯铁材料加工成的U型电磁铁铁芯；④是T型导轨，采用10 mm厚度的镀锌钢材料；⑤是气隙传感器探头，通过铁夹固定在钢轨上方的悬浮架上；⑥是由铝合金材料加工而成的悬浮架.

图9 单电磁铁模型机械结构Fig.9 Single electromagnet model mechanical structure

在图10～12中：示波器通道1测量电流波形，分辨率为2.5 A/div；通道2测量气隙波形，分辨率为4 mm/div.

图10给出了两种控制方式下系统空载（电磁铁等效质量为6.50 kg）起浮时的电流和气隙波形. 由图10（a）可知，电流环采用PID控制的情况下，系统起浮瞬间电流迅速增加，最大达到15.0 A，于此同时悬浮气隙减小，经过0.50 s的调整达到稳定状态，但在调节过程中电流和气隙均出现多次波动. 由图10（b）可知，电流环采用D-OCC的情况下系统起浮时峰值最大电流约为13.0 A，随着悬浮气隙的减小电流减小，大约需要0.40 s的调整系统可以稳定.两种控制方式下系统稳定在给定气隙6.5 mm时，电流稳定在3.0 A.

图10 单周期电流控制悬浮系统起浮实验波形Fig.10 Experimental waveform of floating condition in EMS using current D-OCC

图11 给出了两种控制方式下系统稳定悬浮时50%（3.25 kg）加减载情况下电流和气隙实验波形.由图11（a）可知，电流环采用PID控制，加载瞬间电流出现较大波动，峰值达到7.0 A，对应的气隙出现约为3.5 mm的波动，经0.50 s调节达到稳态，此时气隙值为 6.5 mm，电流值为 3.8 A. 由图 11（b）可知，电流环采用D-OCC，系统加载瞬间，电流最大值约为5.0 A，同时存在2.0 mm气隙波动，经0.20 s调整气隙恢复至6.5 mm，电流稳态在3.8 A. 系统进行50%减载瞬间，气隙与电流出现相同趋势减小，最终气隙恢复设定值，电流稳态值由3.8 A减小至3.0 A，但在减载过程中电流及气隙调节过程都比较平稳.

图12 给出了两种控制方式下系统稳定悬浮时施加1.0 mm脉冲气隙扰动的实验波形. 由图12（a）可知，在电流环采用PID控制的情况下，遇到1.0 mm气隙扰动时，电流和气隙会产生较大波动，电流波动的最大值为6.0 A，气隙波动约为2.5 mm，经过0.50 s调整恢复至稳定. 由图12（b）可知，在电流环采用D-OCC的情况下，遇到1.0 mm的脉冲气隙扰动时，电流值波动的最大值为5.0 A，气隙波动约为1.0 mm，经过约0.70 s调整系统重新恢复稳定. 实验结果表明，电流环采用PID控制对气隙扰动比较敏感，可以快速调整，但调整过程中电流和气隙波动较大，而电流环采用D-OCC调整过程中波动较小.

综上比较，电流环采用D-OCC的EMS可以实现稳定悬浮，且具有良好的抗负载扰动和抗气隙扰动性能，与电流环采用PID控制相比，在起浮、加减载及气隙扰动情况下，动态调节过程更平稳. 由于实验系统漏磁、轨道气隙不均匀等因素，实验与仿真结果变化趋势相同，但具体数据存在一定差距.

4 结 论

本文对EMS悬浮斩波器的D-OCC算法进行了详细推导，并将采用D-OCC的电流环投入悬浮系统中进行仿真和实验. 可以得出以下结论：

（1） D-OCC算法简单，易于实现，较模拟单周控制具有控制灵活、可移植性强、便于调试等优点；

（2） 仿真及实验结果表明采用D-OCC的电流环能够实现对指令电流快速准确跟随，电流环采用D-OCC满足悬浮系统工作要求，与电流环采用PID控制相比具有较平稳的调节性能，且具有优良的抗干扰性能.

（3） 本文的D-OCC算法是在悬浮电磁铁处于某一额定悬浮点，即将线圈电感理想化为常数的情况下推导得出的. 因此需要控制系统的外环具有良好的调节能力，使电磁铁维持平衡点附近，使该算法趋于准确. 在后续的研究中，可以对线圈电感参数进行在线识别，从而使该算法不受外环控制性能的约束.