地下工程裂隙型涌水超前注浆治理方法

刘人太 ，郑 卓 ，李术才 ，张庆松

（山东大学岩土与结构工程研究中心，山东 济南 250061）

裂隙型涌水是地下工程建设中常见的工程灾害，常采用注浆方法对其进行治理. 近年来，学者们针对裂隙注浆问题开展了大量理论研究及工程实践工作[1-4]：（1） 理论方面，许多学者就裂隙中的浆液扩散规律展开研究. 基于“单一平板裂隙”模型进行了公式推导，依据不同浆液的性质，得到了一系列平板裂隙浆液扩散方程. 但是，在复杂裂隙网络浆液扩散方面的研究较为匮乏. （2） 工程实践方面，伴随着我国众多地下工程建设，在注浆材料选取、注浆工艺选择等方面，取得了一系列的宝贵经验. 但仍需要开展更深入的研究工作，以及更强有力的理论支撑来指导实践.

由于岩体中的裂隙网络十分复杂，存在空间不均一性，同时存在许多尺寸微小的裂隙，可注性差，导致裂隙涌水治理难度较大[5-8]. 而在注浆过程中，裂隙形态及展布情况对浆液扩散具有显著影响. 在对隧道进行超前注浆时，由于掌子面前方围岩中裂隙网络的空间分布难以全部查明，并且对裂隙中浆液流动规律认识不足，导致注浆材料、注浆方法的选择缺乏依据，影响了注浆设计与注浆施工过程中的正确决断[9-10]. 同时，对超前注浆的堵水加固效果缺乏有效预测方法，盲目地开挖可能会诱发工程事故[11].

鉴于以上原因，本文依托于现场试验，尝试运用了裂隙岩体注浆的一系列新理论与新方法；通过钻探获取裂隙频率与渗透系数的信息，并采用统计方法获得其分布规律；借助于涌水量计算理论，结合渗漏水控制标准，建立了注浆材料的选择依据；根据所选注浆材料分析了浆液扩散规律并确定了注浆方法与注浆参数. 采用流动维度理论对注浆过程中PQT曲线进行了分析. 注浆结束后，通过变差函数及克里格法对注浆封堵效果进行了评估，分析并揭示了裂隙岩体注浆封堵机理.

1 工程概况

济南钢城矿业有限公司张马屯铁矿位于济南市东郊张马屯村附近，为接触交代矽卡岩型铁矿床，是济南铁矿区中重要矿床. 山东大学针对其开展了多个注浆堵水工程，取得了良好成效，矿床于2012年2月29日正式投入生产. 其中，Ⅱ矿体及与成矿有关的灰岩大致成俘虏体状态插入闪长岩体内，矿体埋藏浅，上部为第四纪表土及风化闪长岩，下部与大范围灰岩相连，其中第四纪表土层厚度30～40 m，含水丰富，风化闪长岩厚度约10 m. 矿体顶部围岩风化严重，稳固性差，矿体下部灰岩裂隙较发育，矿体开采受地表水及矿体灰岩水威胁. 为保障矿床安全开采，应针对矿床上部及下部围岩开展地下水防治工作，形成矿体上部及下部隔水层，保障围岩稳定性及阻水性，达到对矿体内井巷及采矿工程的有效防护，实现矿床安全开采. 在本文的研究中，针对一掘进过程中渗漏水较大的运输巷道，应用本文中的注浆理论与方法开展现场试验，对地下水实施超前注浆封堵，并根据开挖后封堵效果，对其有效性进行评判.

2 裂隙渗透系数及隙宽数理统计

裂隙岩体注浆是一个浆液与围岩相互作用的过程，裂隙的展布规律对浆液扩散具有重大影响. 因此在注浆施工前，应尽量探明围岩中裂隙频率、渗透系数、隙宽等地质信息，为注浆材料与注浆方法的选择提供依据. 基于此，本次现场试验首先开展了围岩钻孔探查工作，根据所获得的地质信息计算得出了裂隙渗透系数及隙宽统计规律.

2.1 地质信息钻孔探查及现场压水试验

本次现场试验段长为30 m. 试验首先通过地质信息钻孔探查的方法获取了围岩内裂隙分布以及渗透性信息. 采用钻孔取芯以及钻孔电视分析方法，获取了钻孔所揭露的裂隙信息，以1 m为分段间隔，对每个段长内所包含的裂隙数量进行了统计，结果如图1所示.

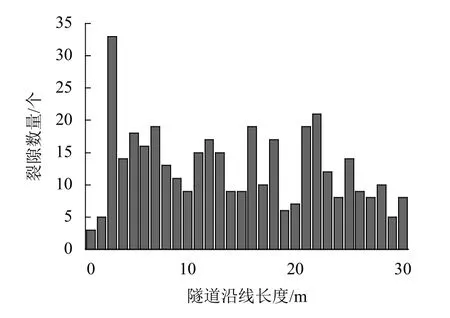
图1 裂隙频率分布Fig.1 Fracture frequency distribution

通过分段压水试验的方法，对围岩的渗透系数进行了测定. 在压水试验过程中，针对裂隙岩体的渗透性采取了各向同性的假设，认为压入岩体裂隙中的水流均沿径向流动. 当压入的水流达到稳定状态后，记录观测孔内的孔隙水压力和压水孔内的水压力，从而计算出岩体的渗透系数. 试验获得了隧道沿线各段长内的渗透系数变化情况，其结果如图2所示.

然而，仅仅获取渗透系数尚不足以对注浆设计形成有效的指导，还需要设法查明裂隙宽度的分布情况. 对于某一特定的隙宽而言，不同类型的浆液其渗透能力有所不同. 对于颗粒型浆液来说，当浆液中颗粒粒径与隙宽相差不大时，会受到滤过作用影响，而当粒径大于隙宽时，浆液将无法注入.

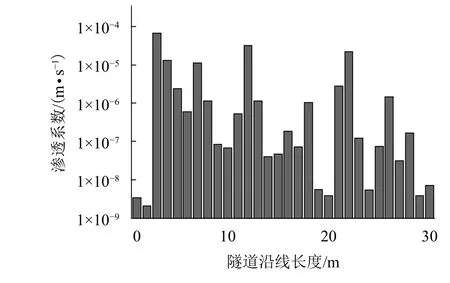
图2 渗透系数分布Fig.2 Permeability distribution

裂隙宽度的获取可采用水力学方法，用岩体渗透系数计算裂隙宽度. 由于渗透系数由裂隙宽度、间距、裂隙组数、裂隙内的填充物、连通状况、裂隙面的粗糙度等众多因素共同决定，是一个多元函数，因此计算得到的裂隙宽度往往具有多解性. 本文中采用立方定律计算等效隙宽作为近似代替，其表达式为

式中：b为计算的等效隙宽；T为渗透系数；μw为水的动力粘度；ρw为水的密度.

2.2 基于现场试验的裂隙渗透性统计分布

本次现场试验通过超前钻探与压水试验的方法获取了试验段内各段长的裂隙数量以及渗透性信息. 由于在压水试验过程中，较小隙宽裂隙的渗透性会被隙宽较大的裂隙所掩盖，导致所测得的渗透性与实际有较大出入. 考虑到以上限制，本文借助统计学方法，根据现场试验中所测得的裂隙样本，分析得到其统计规律，从而获取岩体裂隙网络中隙宽与渗透性的整体信息.

假定钻孔揭露的裂隙组是由相互平行的裂隙构成，裂隙之间相互隔离，此时地下水在裂隙中的流动是二维流动. 因此，裂隙岩体总的渗透系数应为各裂隙的渗透系数之和. 根据Gustafson等学者的研究理论，若裂隙网络中有少数较大的裂隙以及许多微小裂隙时，则裂隙渗透系数近似服从于帕雷托分布，可运用数理统计方法计算其分布规律[12]. 若用P（Tn）来表示所有裂隙中渗透系数小于Tn的概率，则各裂隙渗透系数与其在所有裂隙中所占的比例可以表示为

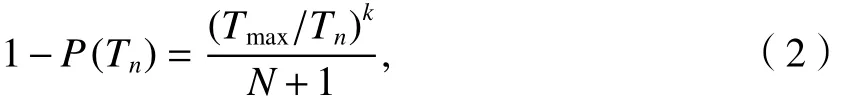
式中：Tn是总数为N的裂隙样本中按大小排序为n的裂隙渗透系数；Tmax为最大裂隙的渗透系数.

将式（2）两边取对数，得到

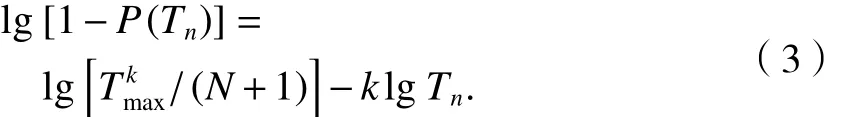
因此，若渗透系数符合帕雷托分布，则在对数坐标中分布曲线将是一条直线，其中k为直线的斜率.获得样本后，可根据最小二乘法拟合出直线方程并得到相应的k值.

通过立方定律，可进一步对隙宽的分布进行计算. 将立方定律做以下变形：

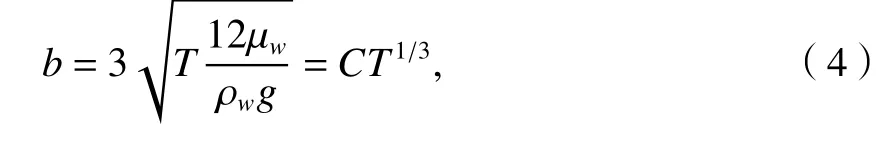
其中，C可近似认为是常数，则

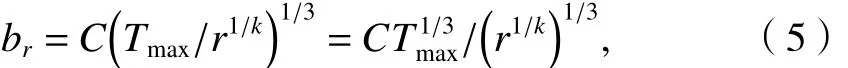
即

式中：br为裂隙样本中按隙宽大小排序为r的裂隙宽度；bmax为裂隙样本中的最大隙宽.

因此，等效隙宽服从参数为3k的帕雷托分布.

基于以上分析，可以通过数理统计的方法，对本次现场试验所获取的裂隙隙宽以及渗透系数等信息进行计算分析，从而获得裂隙等效隙宽的统计分布规律. 首先，依照帕雷托分布函数对本次现场试验中各段长的渗透系数进行拟合，计算结果如图3所示.由图3可见，在10-9～10-4m/s的范围内，渗透系数分布函数在对数坐标中近似呈一条直线，通过最小二乘法进行回归分析，计算得到直线斜率为 - 0.248，即k = 0.248，其相关系数为0.89. 将其代入式（6），可进一步得到等效隙宽的分布函数，计算结果如图4所示，图中，P（br）为 b ＜ br时的概率.

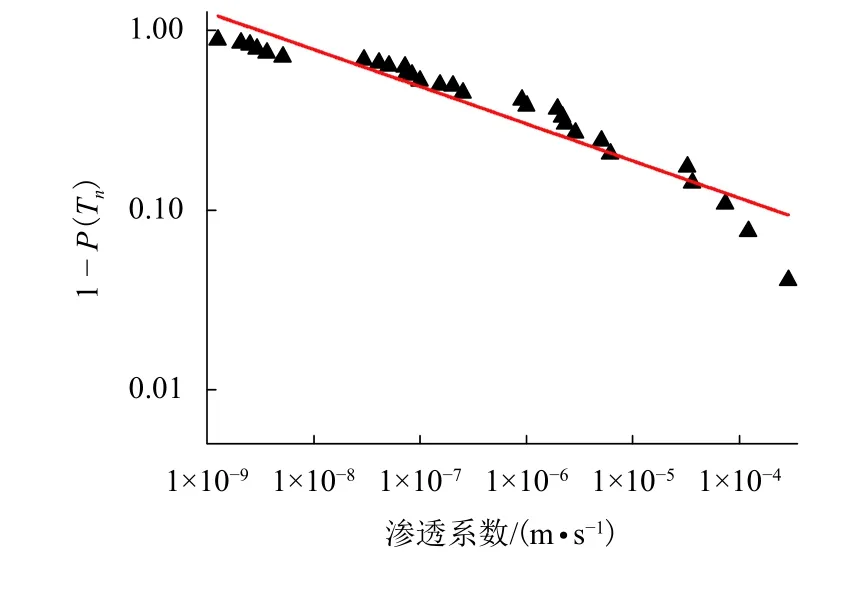
图3 渗透系数拟合曲线Fig.3 Permeability fitted curve

图4 基于现场试验的等效隙宽统计分布Fig.4 Calculated hydraulic aperture based on the results of field test

3 注浆治理前后涌水量预测方法

获得围岩裂隙频率及渗透系数分布之后，即可对涌水量进行预测. 涌水量预测可采用Hawkins[13]提出的公式计算，如式（7）.

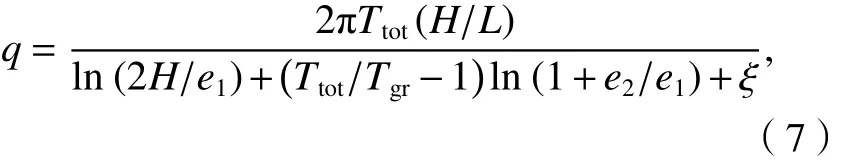
式中：q为注浆治理后单位长度涌水量；Ttot为治理区域内裂隙渗透系数总和，可按式（8）计算；H为地下水头高度；L为治理区域长度；rt为当量半径；Tgr为对隙宽大于最小封堵隙宽bmin的裂隙封堵后裂隙渗透系数总和；e1为隧道的主量半径；e2为注浆加固圈厚度；ξ为经验系数.

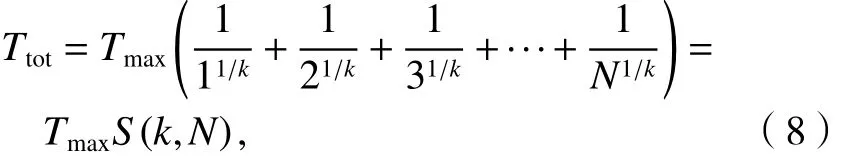
使用式（7）相应的假设：认为岩体裂隙内地下水流动为二维平面流，并且为稳态流动，H不随时间变化. 当对其他各参数赋值后，该式可反映出隧道内涌水量与注浆治理后围岩的渗透系数的定量关系. 该式有两方面的用途：依据设计时确定的涌水量容许值，可以计算出相应的Tgr，再根据立方定律反算需要封堵的裂隙宽度的最小值，为注浆材料的选择提供依据；当选定了注浆材料与注浆方法后，就可以确定出所封堵的最小隙宽，再根据式（7）计算出注浆治理后的涌水量，对治理效果做出预判. 通过式（7）可以看到，治理后的涌水量不仅与最小封堵隙宽有关，同时也与参数ξ有关，然而对于较小的等效隙宽，ξ的变化对涌水量的影响可以忽略.

4 注浆材料优选

由于试验段存在较多的微小裂隙，因此选择超细水泥作为主要注浆材料. 在对浆液性能进行测试时，重考虑浆液可注性，满足设计涌水量对注浆治理的要求. 对于浆液可注性而言，其关键的两个材料参数为临界隙宽bcrit和最小封堵隙宽bmin[14]. 当裂隙宽度大于bcrit时，浆液在裂隙内的流动主要受浆液自身粘度所控制，而不受裂隙的影响. 当裂隙宽度处于bcrit和bmin之间时，浆液在裂隙内流动将受其滤过作用影响，浆液颗粒不断淤积，导致浆液浓度变化，最终扩散距离减小. 当裂隙宽度小于bmin时，浆液无法注入裂隙. 鉴于此，开展室内试验，对浆液理化性质进行测定. 采用比表面积为8 200 cm2/g的超细水泥，共测试了3种具有不同水灰比的浆液，其主要性能如表1所示，表中，t为时间.

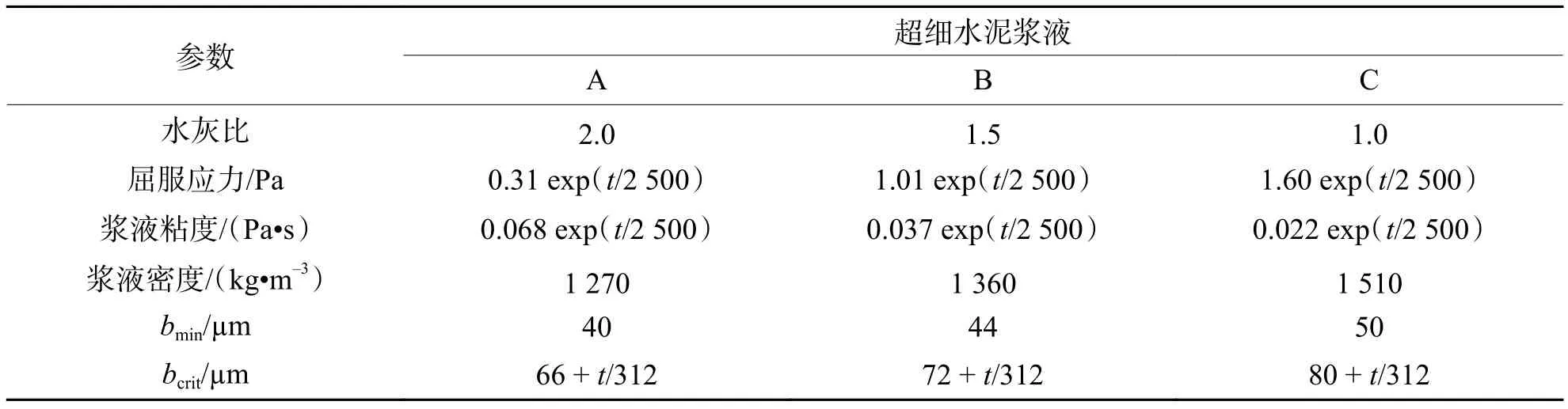
表1 试验测定的不同浆液的物理力学性能Tab.1 Tested physical and mechanical properties of different grout

运用式（8）计算不同bmin对应的注浆后涌水量预测值，其中ξ分别取3、5、10不同的数值，所得曲线如图5所示. 可以发现，当bmin较小时，ξ对涌水量预测值的影响可以忽略. 同时可以看到，若注浆材料选择普通水泥浆液，则封堵后的单位长度涌水量在5 m3以上，因此必须采用超细水泥浆液进行封堵.对于表1中的3种浆液，计算得到的涌水量分别为0.011、0.016、0.020 m3/h. 为保证浆液凝结固化的能力以及凝固后有足够的强度，浆液的水灰比不宜太高，因此选定浆液C作为注浆材料.

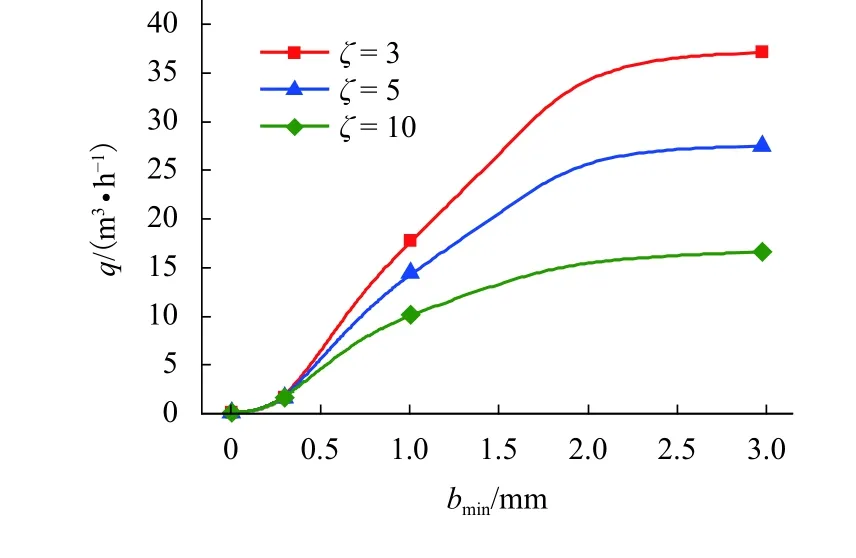
图5 预测涌水量随最小封堵隙宽的变化曲线Fig.5 Variation of predicted inflow according to different smallest sealed fracture

5 浆液扩散距离的确定

注浆过程中浆液运移时空变化规律与极限扩散半径的确定对注浆设计有很大的影响. 许多学者提出了浆液扩散的数学模型，并得到了浆液扩散方程.然而这些结论往往基于不同程度上的简化，在指导注浆设计时与实际有较大出入. 实际工程中，扩散半径的选择往往凭借工程师的经验人为确定. 对于水泥浆液，在土体注浆时，受注介质对浆液扩散具有显著的滤过作用，二者相互作用的力学机制十分复杂.裂隙岩体注浆时，当裂隙宽度大于bcrit时，裂隙对浆液的滤过效应便可忽略不计，浆液扩散距离主要与注浆压力与地下水压力以及浆液的屈服强度有关.Gustafson等[15]给出了水泥浆液在裂隙中的极限扩散距离Imax与裂隙宽度的函数关系为

式中：Δp为注浆孔压力与地下水静压力的差；τ0是浆液的屈服强度.

根据Gustafson等的理论，浆液达到Imax需要经过无限长的时间. 因此定义特征时间

以及相关时间

式中：μg为水泥浆液的粘度.

而相关距离ID仅为tD的函数，具体函数形式则需根据不同的注浆材料性质来确定，而实际扩散距离可表示为

因此，根据ID与tD的关系，可求得任一注浆时间所对应的浆液扩散距离.

6 注浆设计与施工

本次现场试验采用了Butrón等[9]提出的注浆设计流程，如图6所示.

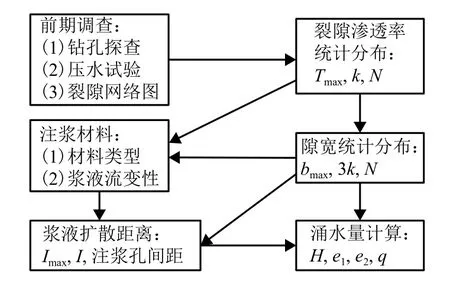
图6 注浆设计流程Fig.6 Grouting design diagram

沿掌子面周线布置注浆孔50个. 依据第5节的浆液扩散距离式（9）～（12），对于大多数裂隙，当注浆压力为2 MPa且注浆时间达到30 min时，浆液扩散距离均在2 m以上. 故第1循环中单孔注浆时间拟定为30 min. 注浆终压控制在4 MPa以内. 设计终孔间距为3 m，保证终孔处浆液扩散具有较大的重合范围，注浆后形成严密的隔水帷幕，注浆加固范围内不存在注浆盲区，钻孔布置平面与剖面如图7所示. 第1循环结束后，对注浆孔进行复钻，通过压水试验测定其渗透性，然后进行第2循环注浆.

注浆过程中，对注浆压力、注浆量进行实时监测，得到其PQT曲线. PQT曲线反映了围岩对浆液的阻力以及对浆液流速的影响. 根据Gustafson等学者的研究[8]，浆液在裂隙中流动维度不同，所受阻力以及浆液流速也不相同，流动维度越大，裂隙的导水能力越强. Gustafson等提出了注浆过程中浆液流动维度为

式中：Q、 V 分别为注浆量和注浆速度.

得到的不同W的计算值代表不同的流动维度，当W ＜ 0.45时为管道裂隙流动； W ∈[0.45,1] 时为平面裂隙流动；W ＞ 1时为裂隙网络流动. 因此注浆过程中，可根据PQT曲线对浆液在裂隙的流动维度进行判别，并及时调整注浆方法. 对于一维流动，只需达到注浆压力与注浆量要求即可完成对裂隙的封堵. 对于二维流动，应相应提高注浆量. 当浆液完成对裂隙的完全封堵之后，与之相连的其他微小裂隙由于没有水源补给，也将失去导水能力. 因此，即便浆液颗粒没有扩散进入微小裂隙，但这并不影响对该区域的注浆堵水效果. 对于三维流动，由于裂隙通道相互交错，往往难以对其全面封堵，以致注浆后涌水通道发生转移，因此需增补注浆孔进行注浆.

图7 注浆钻孔布设Fig.7 Grouted borehole layout

7 注浆效果检查

在对所有钻孔注浆结束后，对注浆封堵效果进行检查. 通过钻孔取芯以及钻孔电视探查结果发现，当裂隙隙宽大于1 mm时，浆液在裂隙内扩散较为充分，涌水通道几乎完全被封堵，岩体的渗透系数明显降低. 对于裂隙频率较高且隙宽较小的区段，其渗透性并没有明显降低. 总体而言，注浆治理完成后，裂隙内的二维和三维流动基本消失，只剩下一维水槽流动. 由于裂隙网络中的主要裂隙均已被封堵，使得剩余的微小含导水构造丧失了补给水源通道，其渗漏水威胁也随之降低. 若进一步增加钻孔继续注浆，往往无法揭露其水流通道，因此这一部分地下水难以进一步封堵.

通过开挖揭露的围岩渗水以及浆液充填情况表明：拱顶与侧壁无明显渗水，仅在局部存在滴水，估测涌水量不足0.01 m3/h，达到了开挖对渗漏水的要求以及注浆封堵的目标. 与本文第4小节中采用式（7）计算得到的涌水量相比较，实际开挖后的涌水量比预测值低50%. 其主要原因：式（7）的适用条件为二维流动，而在本次现场试验中，实际岩体内的裂隙是相互交错的，注浆过程中，当对较大裂隙进行封堵之后，与之相连的微小裂隙丧失了补给水源通道，其导水能力也随之降低；注浆改变了围岩的应力场，裂隙面法向应力不断增大. 在浆液充填作用下，岩体的密实程度增大，导致裂隙开度减小，从而使其渗透性进一步降低.

8 结 论

（1） 本文针对裂隙型涌水超前注浆治理开展了现场试验，获取了试验段内各段长的裂隙数量以及渗透性信息. 分析表明样本近似服从于帕雷托分布，并计算得出了裂隙渗透系数及隙宽统计规律.

（2） 基于所获得的隙宽统计分布，以涌水量与最小封堵隙宽的关系式为理论依据，结合室内试验所测得不同浆液的物理力学性能， 完成了对注浆材料的优选，并对注浆治理后涌水量进行了预测. 在裂隙中地下水近似于二维平面流动时，依据涌水量公式计算值高于开挖完成后涌水量的实测值，但处于同一数量级.

（3） 流动维度对注浆封堵效果具有很大的影响.对于二维平面流动，对较大裂隙进行封堵的同时阻隔了微小裂隙的水源补给，使该区域的渗水量明显降低. 对于一维水槽流动，因注浆钻孔无法直接揭露其水流通道，导致难以对其封堵. 对于三维流动，因裂隙通道相互交错，往往难以对其全面封堵，以致注浆后涌水通道发生转移.

（4） 通过分析PQT曲线，对浆液在扩散运移过程中的流动维度进行判断，实现了注浆施工过程的动态调控. 开挖结果表明，注浆封堵取得了良好的治理效果，验证了所采用注浆治理方法的有效性.