胶轮导轨电车走行部结构强度评定方法研究

孙珉堂， 李梁京， 赵峰强， 粘世昌， 李 芾

(1 中车四方车辆有限公司， 山东青岛 266111；2 西南交通大学 机车车辆工程系， 成都 610031)

随着经济的快速发展，城市人口迅速增加，城市拥堵与大气污染问题变得日益严重。国内很多大城市借鉴世界其他发达国家的经验开始兴建立体化的轨道交通系统，以解决日趋严重的交通问题。目前，城市轨道交通系统主要分为使用钢轮-钢轨的有轨电车、地铁及使用胶轮的自导向电车。但是采用钢轮钢轨走行模式的有轨电车在钢轨上行驶时产生振动和噪声，对周围环境的影响已成为限制城市轨道交通发展的突出问题之一[1]。而自导向胶轮电车，具有比地铁投资小、噪声小、工期短，污染小的优点，且对道路要求较低在国内得到迅速发展[2]。

胶轮导轨电车作为自导向胶轮电车的一种，在国内上海张江、天津滨海新区成功运行[3-4]。但是由于该类车辆在国内为首次研发，其车辆结构又介于铁路车辆和公路车辆两者之间，其走行部结构强度没有相应的评价标准，综合现行铁路车辆，提出了用于胶轮导轨电车走行部的结构强度评价方法，并针对设计的胶轮导轨车辆进行强度校核。

1 胶轮导轨电车介绍

胶轮导轨电车走行部分为动力走行部和非动力走行部两种。动力走行部如图2(a)所示，主要由动力轴桥和导向装置组成。拖动走行部如图2(b)所示，主要由承载轴桥和导向机构组成，结构相对简单。

图1 导轨电车编组图

图2 走行部

2 车辆模型

相比非动力走行部，动力走行部结构更为复杂且承受载荷更大，在分析中以动力走行部为例。动力走行部承载结构采用钢板组焊而成的箱型梁，上端上盖板区安装空气弹簧，为垂向载荷输入位置，同时布置垂向液压减振器，下端与轴桥组焊，将车体垂向载荷传递至轴桥。基于ANSYS软件，对各分析结构进行三维实体建模，采用高精度10节点二阶四面体单元Solid92进行网格离散。动力走行部承载构架及导向连杆系统实体模型及有限元网格离散模型如图3～图6所示。

图3 走行部承载构架实体模型

图4 走行部承载构架有限元模型

图5 导向连杆系统实体模型

3 计算载荷及工况

参考铁道车辆走行部的结构强度评定方法TB/T 2637《铁道客车转向架构架、摇枕及摇动台》标准，该车走行部各承载结构的强度计算可考虑两类载荷：超常载荷和正常运营载荷。其中，前者代表走行部在运用寿命期间极少出现的极值载荷；后者代表走行部在正常运营条件下经常出现的数值中等的载荷。相应地，计算载荷工况也分为两类：超常载荷工况和正常运营载荷工况。由图2可知，走行部结构主要包括两部分：汽车轴桥和导向机构，因此走行部设计计算载荷可参照相关汽车和铁道车辆设计标准进行确定。

图6 导向连杆系统有限元计算模型

3.1 超常载荷

3.1.1轴桥评定载荷

垂向载荷：根据参考文献《汽车设计》[6]，汽车轴桥除承受静态载荷外，还承受附加的冲击载荷，该车轴桥动载荷系数可取2.5，因此最大垂向载荷为满载载荷的2.5倍。

横向载荷：主要考虑车辆通过曲线时离心力导致的侧向力载荷，此时车辆处于侧滑的临界状态，最大侧向力载荷即地面给轮胎的侧向附着力。

第2次手术时间（118.53±42.62）min，出血量（85.61±30.83）ml；后路选择性减压4例，神经根症状消失，术后伤口愈合好，没有出现并发症。

纵向载荷：主要考虑电车最大启动牵引力或紧急制动产生的载荷；轴桥与导向机构连接部位考虑导向机构产生的最大5g加速度冲击载荷；

3.1.2导向机构评定载荷

导向机构载荷主要考虑驱动轮胎转向产生的导向力载荷和导向机构安装部位的冲击载荷。超常载荷分别为车辆运行时最大导向力和最大5g加速度冲击载荷。

根据线路试验可知最大导向力载荷为10 kN。

3.2 运营载荷

3.2.1轴桥评定载荷

轴桥运营载荷主要考虑车辆正常运营工况所产生的载荷。

垂向载荷：车辆运行对轴桥产生的垂向载荷。

纵向载荷：车辆运行所需的持续牵引力。

3.2.2导向机构评定载荷

根据线路试验和动力学计算结果可知，车辆正常运行过程中产生的导向力为6 kN，因此导向机构运行载荷取6 kN。

4 强度评定方法

4.1 静强度评定准则

在超常载荷工况作用下，结构不应发生可测量到的整体结构永久变形，其意味着结构危险截面应力不应超过材料的屈服强度。各类焊缝的疲劳许用应力均保守采用ERRI B12/RP17给出的数值。但对于使用塑性材料制造的承载结构，应力计算没有必要考虑所有应力集中，特别是结构局部应力集中。 由于模型在计算时考虑了应力集中效应，运行部分高应力区域的应力值超过材料屈服强度，但应保证屈服强度足够小从而材料不会产生永久变形。

4.2 疲劳强度评定准则

疲劳载荷的评定参照EN和UIC(国际铁路联盟)等设计标准推荐使用的修正Goodman疲劳极限图进行。结构在各种正常运营载荷工况作用下，按最不利组合方式确定出的动应力，应小于制造材质相应的疲劳许用应力。其中，确定承载钢结构各部位动应力的方法和步骤为：

基于结构有限元应力分析技术，分别计算承载钢结构在各种正常运营载荷工况作用下的应力分布结果；

对结构任意部位，首先确定其在各载荷工况下的主应力值，然后取结果值中最大的主应力值为该部位动应力的最大应力σmax， 其余工况向最大应力方向投影。

使用式(1)将其他载荷工况下的各向应力投影至最大应力σmax作用方向，并取投影值中最小者为该部位动应力的最小应力σmin；

(1)

式中：σch,i为第i载荷工况下各向应力沿最大应力σmax作用方向投影应力值；

σxx,i、σyy,i、σzz,i为第i载荷工况下的三向正应力值；

σxy,i、σxz,i、σyz,i为第i载荷工况下的三向剪应力值。

使用式(2)计算出该部位其他动应力参量：

(2)

式中：σm为平均应力；σa为应力幅；R为应力比。

按上述方法确定出各部位动应力相关参量后，即可将其与疲劳许用应力进行比较验证其疲劳强度。本报告中，疲劳许用应力采用EN和UIC(国际铁路联盟)等设计标准推荐使用的修正Goodman疲劳极限线图：将结构各部位的动应力状态点(σm，σmax)和(σm，σmin)放入对应的修正Goodman疲劳极限线图内评定。如图7所示为母材抗拉强度不小于520 MPa的疲劳极限线图。

5 构架计算结果分析

5.1 静强度计算结果

按上述载荷工况即评定准则对计算结果进行静强度评定。结果表明：动力走行部轴桥在所有载荷工况作用下，应力均小于制造材质的许用应力，满足静强度评定要求。最大载荷工况下动力走行部承载构架及导向连杆系统有限元模型计算结果如图8、图9所示。

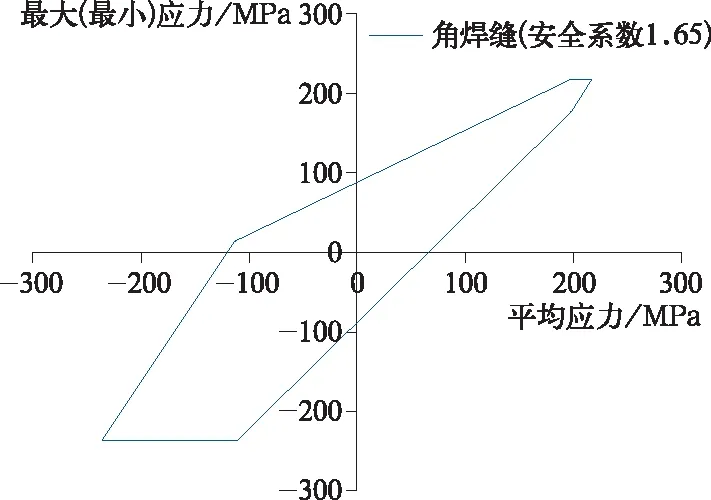
图7 角焊缝修正Goodman疲劳极限线图

图8 动力走行部轴桥静强度计算结果

图9 导向连杆系统静强度计算结果

5.2 疲劳强度计算结果

使用图5所示疲劳极限线图评定动力走行部轴桥及导向连杆系统疲劳强度性能。计算和分析结果表明，动力走行部承载构架组焊梁各焊缝接头部位及导向连杆系统动应力均位于角焊缝修正Goodman疲劳极限线图包络线内，疲劳强度满足评定要求。其动应力校核结果如图10所示。

6 结 论

依据铁道车辆标准TB/T 2637及相关汽车车辆标准，结合胶轮导轨电车走行部的受力特性及运行特性提出，在理论上为胶轮导轨电车走行部的受力计算提供了设计依据，其实用性可通过线路试验进一步进行验证。

图10 动应力校核结果