网格密度对制动盘温度场的计算精度和效率的影响

崔 跃， 高 飞， 符 蓉， 李阳杰

(大连交通大学 连续挤压教育部工程研究中心， 辽宁大连 116028)

对于制动摩擦副在制动过程的温度变化规律，利用有限元计算是一种重要的研究手段。有限元法就是近似求解一个物理现象的偏微分方程，而有限元法又是求解这些偏微分方程的一种手段，即借助离散网格来近似求解每个单元所代表的线性方程，最后通过节点处所代表的平衡方程和边界条件求解整个线性方程组的过程。网格密度代表了求解单元的数量，其数量增加意味着求解方程数量的增加从而提高了计算精度，同时需要的计算时间也增加。因此，网格密度的选择决定了计算过程的计算精度和效率，在这方面，已得到不同领域学者的关注。邓记松[1]在用ANSYS软件对筒体接管进行应力有限元分析时，研究了壳体厚度方向上网格密度(层数NT=2、3、4、5、6)对计算精度的影响，发现网格密度越大，总应力值的精度越高，同时也关注到了在厚度方向划分方法与计算精度的关系。符双学[2]等基于Matlab和APDL软件发现了网格密度(在模型齿宽方向分别划分20、40、80、100、160份)增大，对齿根最大应力和齿面平均变形的精度影响较小，计算出的齿根最大应力差值仅为0.715 MPa，齿面平均变形最大差值仅为0.088 μm。蒋梅荣[3]等发现网格单元数在101 800～403 000范围内，对所计算的溢油传播形态的精度没有明显提高，但电脑计算时间相差了3～6.5倍。在利用有限元法研究制动盘温度场方面，也面临着网格密度选择的问题，杨莺，王刚[4]借助ANSYS有限元软件，在计算制动盘温度时，划分了8 458个网格单元，而吴婧斯[5]借助ABAQUS软件对制动盘划分了4 380个单元，吴波文[6]借助ADINA软件对制动盘划分了5 904个网格单元，可见，不同研究者在计算制动盘温度时，考虑了不同的网格数量和计算软件，但这些不同的计算方法中，采用的网格数量是否合理，计算精度如何保障，都是值得考虑的。因此，针对制动盘温度场的计算，探讨网格单元数对计算精度和效率的影响是有意义的。

文中针对盘面温度场，利用ADINA有限元分析软件，通过设置多种网格数量，研究了网格密度对计算精度和效率的影响。

1 制动摩擦副有限元模型与计算假设条件

考虑到摩擦副结构的对称性，取摩擦副结构的一半建立有限元模型，由于每次制动产生的热量还来不及扩散到轴上，制动就已经完成，所以数值模拟过程中将忽略轴的影响，简化后的三角形摩擦副如图1所示，其中盘做逆时针转动。

假设条件如下：

(1)摩擦系数设为定值，不随制动时间变化；

(2)忽略摩擦过程中磨损的影响，假设制动期间摩擦产生的热量全部被制动盘和闸片所吸收；

(3)制动压力均匀地施加在三角形闸片上；

(4)制动期间，制动盘和闸片的材料参数不随时间变化；

(5)忽略制动过程中的热对流及热辐射的影响。

图1 三角形摩擦副

2 网格划分与边界条件

采用ADINA软件进行有限元模拟，而有限元的核心就是利用离散化的网格进行模拟计算。在ADINA的前处理模块中，一共有3种指定网格密度的方法，即Use End-Point Sizes、Use Length和Use Number of Divisions，采用第3种指定网格细分份数的方法，闸片采用自由网格划分，单元数为2 007个单元；由于制动盘是对称结构，故对其进行了切分，采用映射网格进行计算，通过改变制动盘径向和周向上的细分份数从而探索其网格密度对模拟结果的影响，具体方案如表1所示，此外，闸片与制动盘都采用六面体8节点单元。

表1 网格单元数量方案

三角形摩擦副主要尺寸如表2所示，其中平均摩擦半径是指三角形闸片的外接圆圆心与制动盘圆心的距离，摩擦面积为三角形闸片与制动盘的接触面积。制动盘与闸片的物理参数如表3所示。

表2 制动盘与闸片的几何尺寸

表3 制动盘与闸片的物理参数

模拟条件：制动初速度分别为50 km/h、100 km/h、160 km/h，制动压力为0.5 MPa，制动盘和闸片的初始温度都是20 ℃，热流分配系数方面[7]，制动盘为0.54，闸片为0.46，对流换热系数为100，摩擦系数为0.4。

3 结果分析与讨论

3.1 半径方向网格密度对制动盘温度场的影响

表4是在制动速度50 km/h和制动压力0.5 MPa条件下，针对4种网格密度(A1、A2、A3、A4)模拟的不同时刻盘面最高温度情况，可见，制动时间为1 s时，4种方案模拟的盘面最高温度皆为29 ℃，到3 s时，盘面最高温度皆为34 ℃，到5 s时，盘面最高温度皆为38 ℃，随着制动时间的延长，盘面温度升高，到10 s时，盘面最高温度都达到43 ℃，到15 s时，A1、A3、A4盘面最高温度为44 ℃，A2模拟的盘面最高温度为43 ℃，19 s时，4种方案模拟的盘面最高温度皆为41 ℃。

表5是在制动速度50 km/h和制动压力0.5 MPa条件下，针对4种网格密度(A1、A2、A3、A4)模拟的制动期间盘面最高温度和出现时间情况，可见，网格密度为A1、A2、A3时，盘面最高温度为45 ℃，A4模拟的盘面最高温度为46 ℃；最高温度出现时间方面，A1和A2为14 s，A3和A4为13 s。

表4和表5的结果表明，在制动速度50 km/h，制动压力0.5 MPa条件下，制动盘单元数在3 000～4 500范围内，从盘半径方向改变网格密度对计算结果影响均不明显，4种方案模拟的不同时刻盘面最高温度差值是1 ℃，4种方案模拟的制动期间盘面最高温度差值是1 ℃，4种方案模拟的制动期间盘面最高温度所出现的时间差值是1 s。

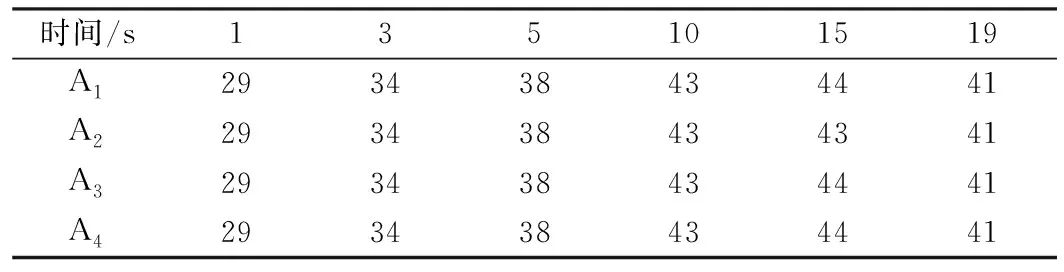
表4 不同时刻模拟的盘面最高温度 ℃

表5 不同方案模拟的制动期间盘面最高温度和出现时间

图2是在制动速度50 km/h和制动压力0.5 MPa条件下，4种网格密度方案(A1、A2、A3、A4)模拟的不同时刻盘面温度分布曲线，可见，4种方案对不同时刻的盘面温度分布曲线影响不大，呈现出相同的变化规律：盘面高温区聚集在91～160 mm范围内，这是因为此摩擦半径范围内是制动盘与闸片的接触区域，制动期间盘的动能转化为热能被制动盘和闸片所吸收，故盘温上升较快；盘面最高温度出现在摩擦半径125 mm处左右，这是由闸片的几何形状决定的，此处摩擦弧长最长，故呈现出此处温度最高，两边温度逐渐放缓的分布趋势；在摩擦半径45～91 mm范围内，盘面热量的主要来源是热传导，制动后期热传导作用增强，故制动前期此范围内盘面温度几乎等于室温，制动后期，盘面温度有所上升。

图2 不同时刻盘面温度分布曲线(50 km/h,0.5 MPa)

3.2 圆周方向网格密度对制动盘温度场的影响

表6是在制动速度50 km/h和制动压力0.5 MPa条件下，针对4种网格密度(B1、B2、B3、B4)模拟的不同时刻盘面最高温度结果，可见，制动时间为1 s时，4种方案模拟的盘面最高温度皆为29 ℃，到3 s时，盘面最高温度皆为34 ℃，到5 s时，盘面最高温度皆为38 ℃，随着制动时间的延长，盘面温度不断升高，到10 s时，盘面最高温度都达到43 ℃，到15 s时，盘面最高温度皆为44 ℃，制动结束时，盘面最高温度皆为41 ℃。

表6 不同时刻模拟的盘面最高温度 ℃

表7是在制动速度50 km/h和制动压力0.5 MPa条件下，针对4种网格密度(B1、B2、B3、B4)模拟的制动期间盘面最高温度和出现时间结果，可见，B1、B2、B3、B4模拟的盘面最高温度皆为45 ℃；在模拟最高温度所出现的时间方面，B1、B3、B4为14 s，B2为13 s。

表7 不同方案模拟的盘面最高温度、出现时间

表6和表7的结果表明，制动速度50 km/h，制动压力0.5 MPa，制动盘单元数在3 000～4 500范围内，从盘圆周方向改变其网格密度对不同时刻盘面最高温度，制动期间盘面最高温度及制动期间盘面最高温度所出现的时间方面影响均不明显，4种方案模拟的不同时刻盘面最高温度相同，4种方案模拟的制动期间盘面最高温度相同，4种方案模拟的制动期间盘面最高温度所出现的时间差值是1 s。

图3是在制动速度50 km/h和制动压力0.5 MPa条件下，4种网格密度方案(B1、B2、B3、B4)模拟的不同时刻盘面温度分布曲线，可见，4种方案对不同时刻的盘面温度分布曲线影响不大，4条曲线几乎重合，不同时刻的曲线变化规律与图2类似。

图3 不同时刻盘面温度分布曲线(50 km/h,0.5 MPa)

3.3 网格密度对计算时间的影响

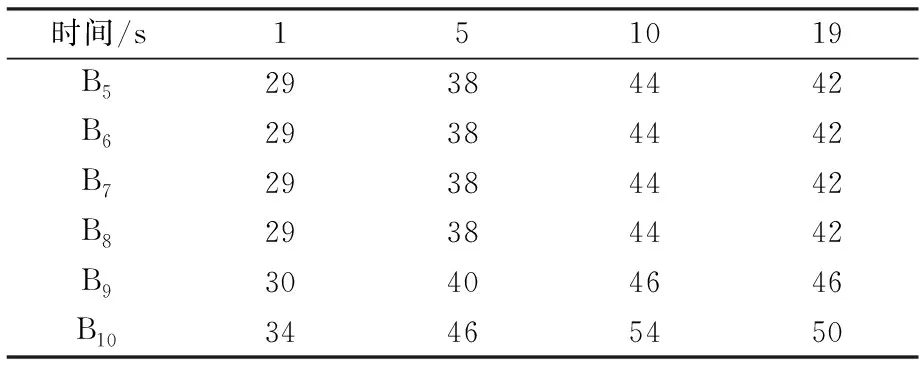
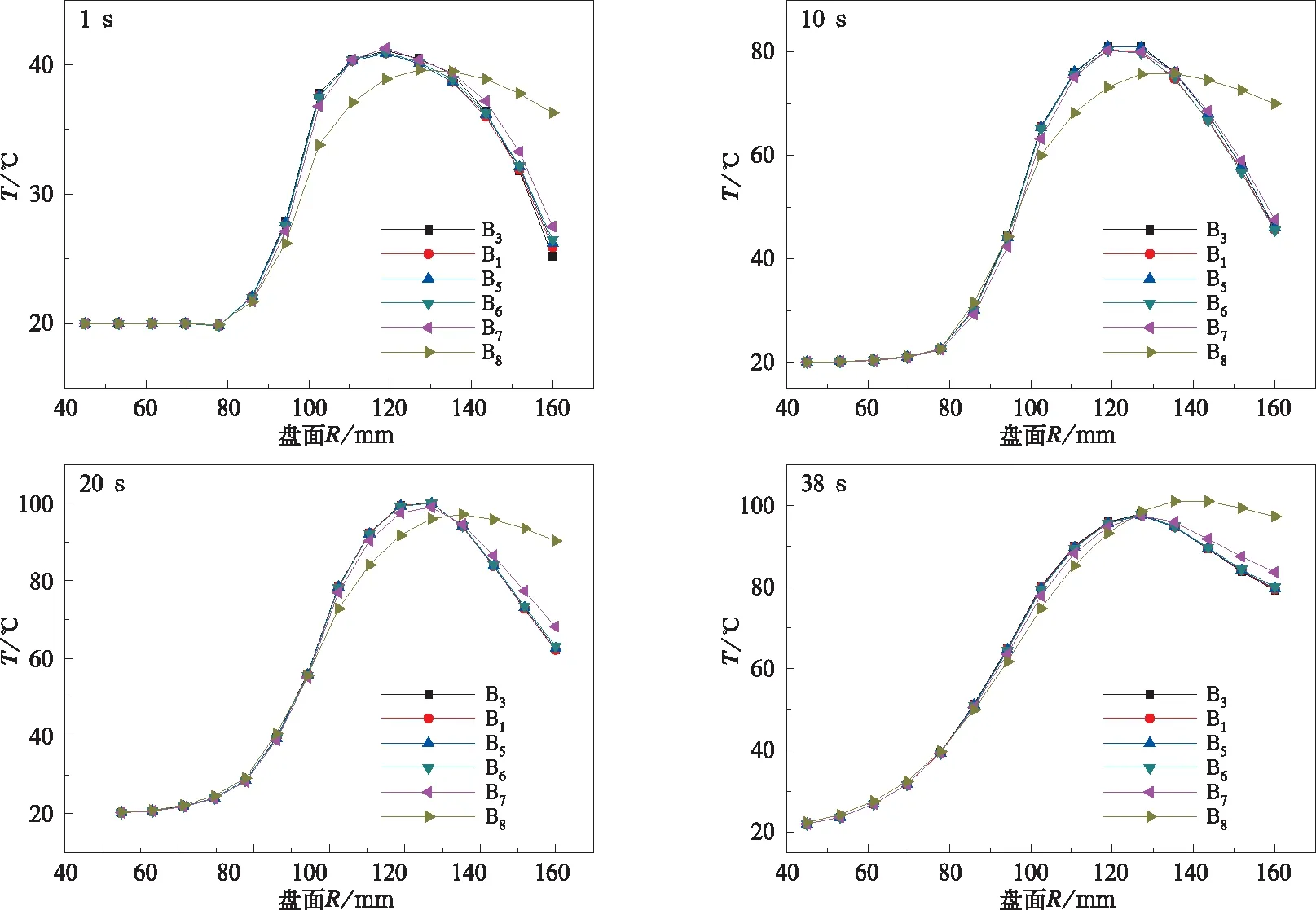
图4是在制动速度50 km/h和制动压力0.5 MPa条件下，半径方向4种不同网格密度(A1，A2,A3,A4)和圆周方向4种不同网格密度(B1，B2,B3,B4)的计算时间对比情况，制动盘单元数相同时，二者差值Δ=(Ai-Bi)/Bi×100%，式中Ai和Bi分别是半径方向和圆周方向的相关物理量(i=1、2、3、4)。可见，A1，A2,A3,A4的计算时间关系为A1

图4 网格密度对计算时间的影响

3.4 最佳网格密度研究

表8是在制动速度50 km/h和制动压力0.5 MPa条件下，不同网格密度方案模拟的不同时刻盘面最高温度，可见，B5至B8方案在不同时刻模拟的盘面最高温度是相同的，B9和B10方案模拟的盘面最高温度出现差别。

表8 不同时刻模拟的盘面最高温度 ℃

表9是在制动速度50 km/h和制动压力0.5 MPa条件下，不同网格密度方案模拟的制动期间盘面最高温度、出现时间及计算时间情况，可见，B5至B8的盘面最高温度相同，数值是45 ℃；B9和B10的盘面最高温度分别是48 ℃和55 ℃，出现了一定的偏差；出现时间几乎相同，计算时间方面，制动盘单元数越少，计算时间越短。

图5是在制动速度50 km/h和制动压力0.5 MPa条件下，6种不同网格密度方案模拟的不同时刻盘面温度分布曲线，可见，B5、B6、B7模拟的盘面温度分布曲线几乎重合，B8、B9、B10模拟的温度曲线与其比较可以发现，在摩擦半径91～160 mm范围内发生了不同程度的偏移，不符合盘面温度分布规律，所以B8、B9、B10方案中制动盘的网格密度是不合理的。制动盘网格密度不同造成盘面温度分布曲线有差异的原因分析如下：有限元是先把要分析的模型做离散化处理分成有限个单元(网格划分)，单元与单元之间用节点相连，一般情况下网格密度越大，划分网格后的模型与实体模型越接近，相应的计算结果越精确，如图6是制动盘网格密度不同时的图案分布，制动盘单元数为200时，制动盘网格图案是一个四边形，制动盘单元数为300时，制动盘网格图案是一个六边形，制动盘单元数为500时，制动盘网格图案是一个十边形，制动盘单元数为1 000时，制动盘网格图案较接近于圆形。此外，4种网格图案在实体制动盘上的覆盖面积分别是63.7%,82.7%,93.5%和98.4%，由此可知，网格单元数越少，划分网格后的图形在实体制动盘上的覆盖面积越小，导致实体模型中不参与计算的部分越多，从而导致计算出的结果与理想结果相差甚远。

表9 不同方案模拟的盘面最高温度、出现时间及计算时间

图5 不同时刻盘面温度分布曲线(50 km/h,0.5 MPa)

图6 制动盘单元数不同时图案分布

图7 不同时刻盘面温度分布曲线(100 km/h,0.5 MPa)

图8 不同时刻盘面温度分布曲线(160 km/h,0.5 MPa)

综合表9中计算时间和图5的结果，可见，在制动速度50 km/h和制动压力0.5 MPa条件下，B7方案在满足精度要求的前提下且用时最少，为了验证B7是最佳方案，对速度为100 km/h和160 km/h时进行了模拟。

由图7和图8可知，制动盘单元数对盘面温度场的影响规律与图5类似，证明了制动盘单元数为1 000(B7方案)时，能达到精度与计算时间的完美结合。

4 结 论

(1)制动盘单元数决定了计算效率，当单元数由300增加到4 500，计算时间从6.4 h延长到20.15 h。此外，划分方法与计算时间也有关，相比于从盘半径方向划分，从盘圆周方向划分更能提高计算效率，二者计算时间最大差值为7.59%。

(2)网格密度决定了计算精度，网格密度越大，划分网格后的计算模型与实体模型越接近，计算精度越高。当网格在实体模型上的覆盖率达到98.4%(制动盘单元数为1 000)时，计算精度已达到100%。