加聚合物型减阻剂环状流摩阻系数新显式方程

李 雷 代晓东,2 郝勇超

1. 中国石油大学胜利学院油气工程学院, 山东 东营 257000;2. 中国石油大学国家大学科技园博士后工作站, 山东 东营 257100

0 前言

专家预计，“十三五”末中国长距离输送油气管道总长度将超过16×104km[1]。在控制成本的前提下,需要满足一定输送量的同时还必须保持一定的输送压力。总之,如何实现管道输送降本增效的目标是一个难题,而向输油管道中加入聚合物型减阻剂是解决该问题的有效途径[2]。摩阻系数的准确预测决定着其他设计参数,比如管路压降。在石油与天然气工业中,普遍存在管内气液两相流,由于气体速度较快,一般情况下均形成环状流[3]。因此,预测加入聚合物型减阻剂环状流摩阻系数具有重要意义。

对于层流,摩阻系数是雷诺数的函数,但是对于湍流,摩阻系数是相对表面粗糙度和雷诺数的复合函数。Blasius H[4]提出了第一个摩阻系数关系式,主要用于光滑管壁数据的曲线拟合,该方程的适用范围为雷诺数小于1×105。普朗特基于光滑管对数速度分布和实验数据推导出了一个更精确的方程[5],该方程的适用范围为雷诺数大于4 000,由于该方程是隐式方程,因此需要进行迭代求解。但最新研究表明，普朗特摩阻系数关系式的常数不适合外推至高雷诺数,因此Mckeon B J等人[6]又提出了一个新式摩阻系数方程。Nikuradse J[7]对湍流管流进行了详细研究,提出了一个计算粗糙管壁摩阻系数的近似方程。许多学者也提出了多种适用于过渡粗糙区的公式[8]。自21世纪以来,针对摩阻系数的计算问题部分学者引入了隐式函数[9-10]。例如,针对计算管流和槽流中光滑/粗糙壁面湍流摩阻系数,Avci A等人[9]提出了一个基于对数速度分布的显式方程,并且利用已发表文章中的实验数据确定了该模型的常量。Shyam SS等人[11]基于人工神经网络方法,建立了一个计算塑性流体在层流/湍流条件下的摩阻系数的显式方法。Taler D[12]提出了最常用的光滑管摩阻系数的显式关系式。

针对单相流中摩阻系数的计算,已经积累了大量的研究经验,但针对环状流摩阻系数的计算研究较少[17-19]。本文将通过对已公布的实验数据进行量纲分析和曲线拟合,基于边界层中对数速度分布和幂律分布推导一种适用于环状流的新显式方程。

1 摩阻系数预测模型

1.1 控制方程

在充满流体的均匀直径圆管中,流体粘滞效应导致的压力损失与管长成比例,压力损失可以通过达西公式来计算[20]:

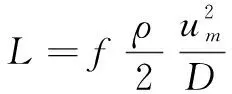
(1)

式中:Δp/L表示单位长度的压力损失,Pa/m;ρ表示流体的密度,kg/m3;um表示平均流速,m/s;f表示摩阻系数;D表示管道直径,m。

摩阻系数由某些参数确定,并且不是一个常量,例如输油管路的表征参数(直径、粗糙高度),流体性质(运动黏度),流体流速。可以将摩阻系数方程应用于不同类型的流动,包括层流,过渡区,光滑/粗糙管完全湍流和自由表面流。圆管层流摩阻系数方程为:

(2)

式中:Re为雷诺数。

加入聚合物型减阻剂，可以减少垂直于壁面方向上气液两相流的雷诺剪应力和速度脉动。对于不加入和加入聚合物型减阻剂的气液混合物摩阻系数fm、 fMD分别见式(3)和式(4):

(3)

(4)

许多学者提出了两相流摩阻系数预测公式。例如,Al-Sarkhi[16]提出式(5)：

(5)

式中：Vsg为气相速度，m/s;Vsl为液相速度，m/s。

本研究的目的是针对加入聚合物型减阻剂的环状流,建立一个预测其摩阻系数准确度更高的新型公式。

1.2 数学模型

边界层中的对数速度分布和幂律分布是摩阻系数方程的基础,管内典型速度剖面见图1。

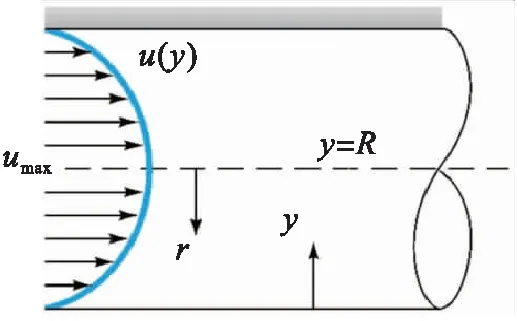
图1 管内典型速度剖面

重叠区中速度呈对数变化,该层称为对数重叠层[11]。

(6)

(7)

式中:y=R-r，K、N为实验确定的常数。

假设式(7)中r=0,最大速度可通过式(8)计算:

(8)

由于计算环状流的摩阻系数前需要确定速度分布,因此为了获得管内平均流速,应对式(7)进行积分。但由于对该方程的积分较困难,因此假设平均流速um是最大速度的一部分,尽管式(8)中针对各种流动的常量取值不同,但是平均速度仍具有相同的格式,因此平均流速可通过式(9)描述:

(9)

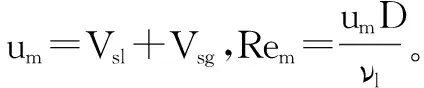
针对加入聚合物型减阻剂的气液混合物,利用量纲分析确定达西公式中的摩阻系数[11]:

(10)

(11)

将式(9)与式(11)联立得:

(12)

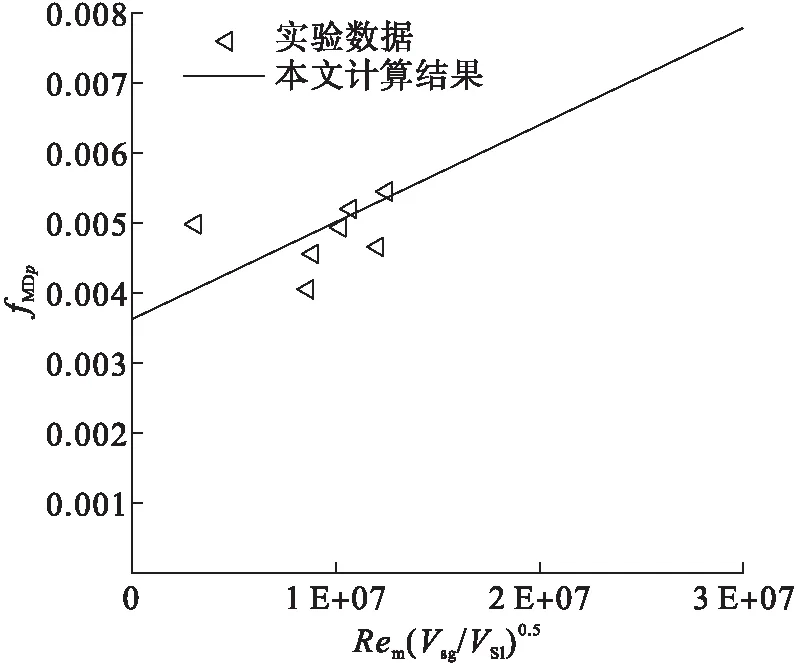
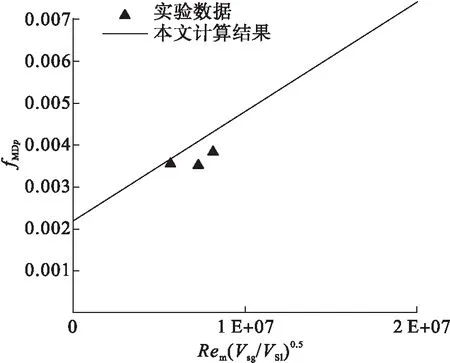
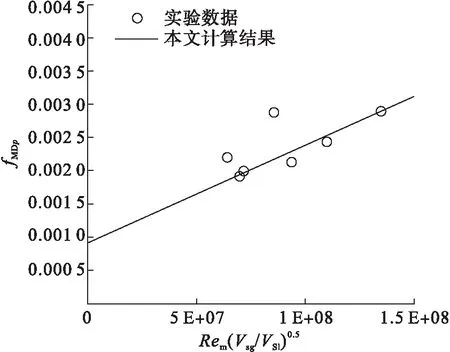
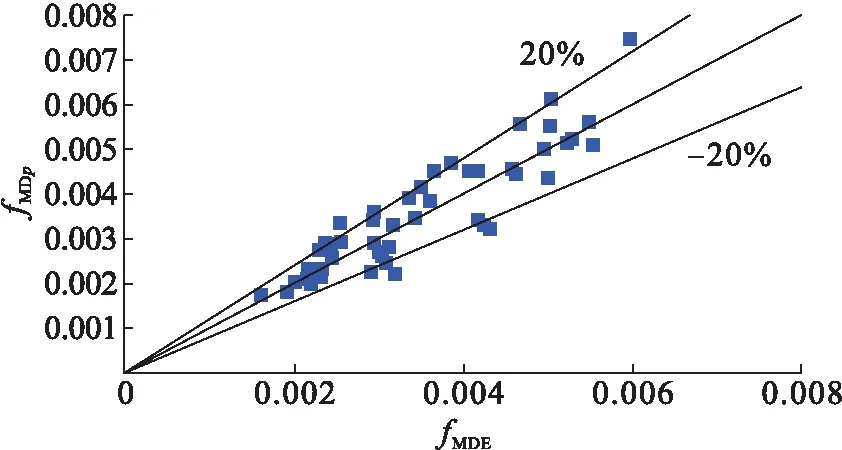
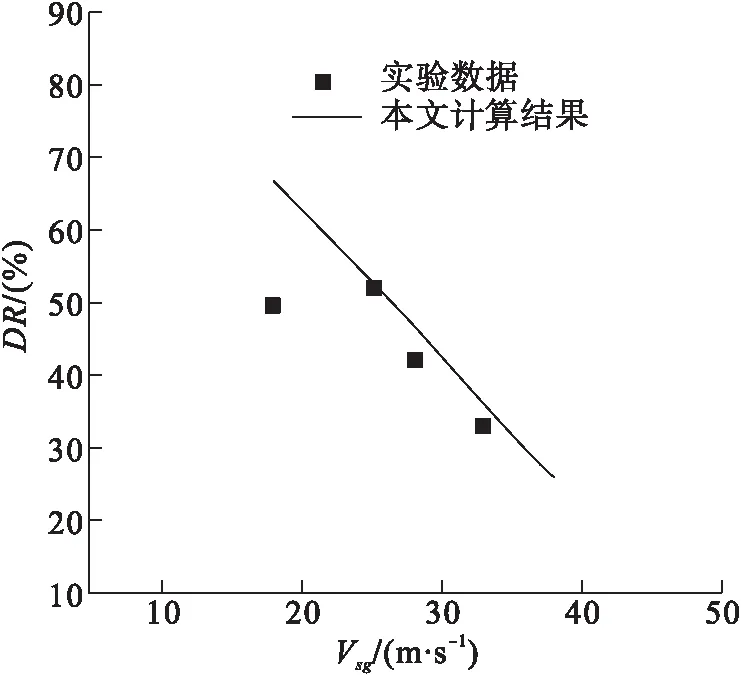
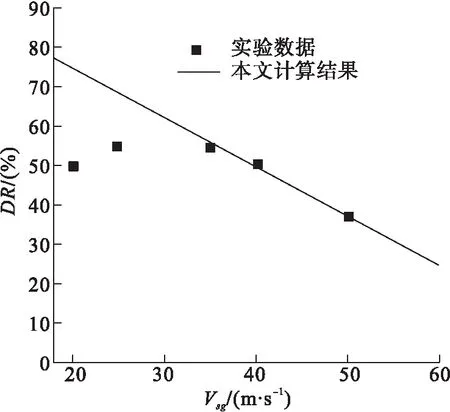
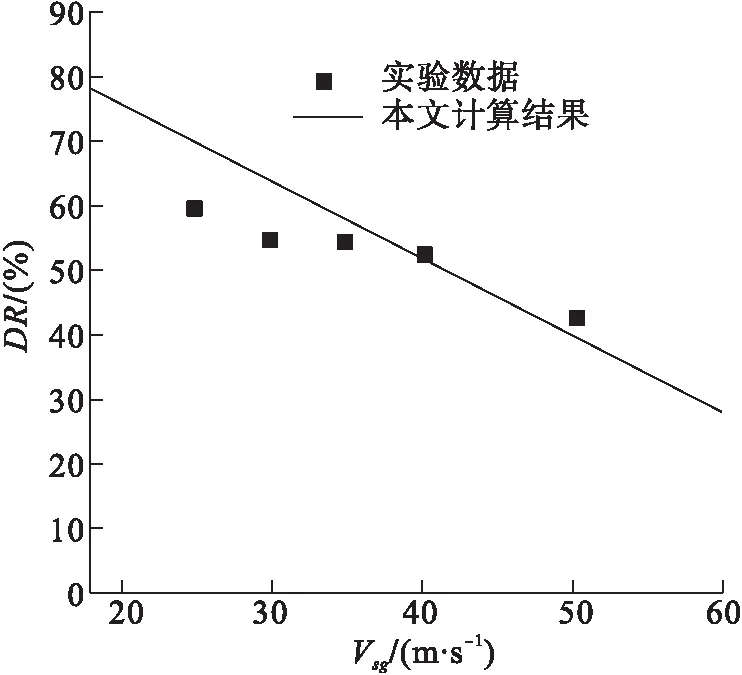
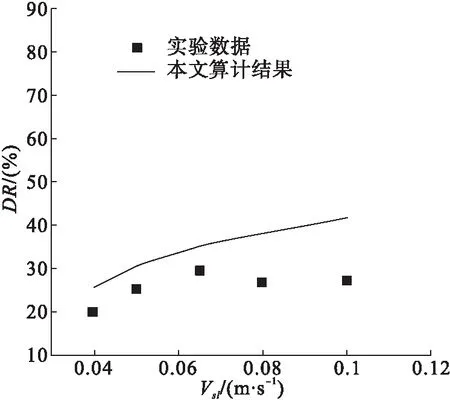
式(12)适用于2.4×105

(13)

式中:系数a1、a2和b由实验数据和最小二乘法得到。在该方法中,参数S由式(14)定义:

(14)

式中:n为实验数据编号;fMDE为加入聚合物型减阻剂的气液混合物的实验摩阻系数。

最小二乘法中,参数S对参数a1、a2和b分别求导如下:

(15)

(16)

(17)

同时联立式(15)～(17)求解,求得a1、a2和b,a1=1.319×1020、a2=158、b=-6.4,将a1、a2和b代入式(13)得，加入聚合物型减阻剂气液混合物的计算摩阻系数fMDP:

(18)

1.3 模型的验证

不同管径对应的fMDp与fMDE见图2。针对不同直径的输油管路,利用式(16)计算加入聚合物型减阻剂的气液混合物混合摩阻系数fMDp,并且基于图2中的实验数据[17]fMDE验证计算结果。此外,引入参数fMD(D0/D)-1与实验数据进行对比,计算结果与实验数据拟合度较好，见图3。

a)D=0.012 5 m

b)D=0.001 9 m

c)D=0.025 0 m

d)D=0.095 3 m

图3 fMD(D0/D)-1预测值与实验数据的对比

2 结果分析

针对加入聚合物型减阻剂的气液混合物,利用Al-Sarkhi(fMDAL)计算fMDp和摩阻系数,并与fMDE[17]相比较,结果见图4。fMDp和fMDE之间的拟合度要好于fMDAL和fMDE。计算结果的平均绝对百分偏差与标准差见表1,同时也表明了利用式(16)计算的精度。减阻率DR定义为使用聚合物型减阻剂DRP(fMDp)的摩阻系数减少值与不使用聚合物型减阻剂DRP(fm)的摩阻系数之比值:

(19)

式中:fm和fMDp分别利用式(3)与式(18)进行计算。

将与气体流速和液体流速对应的减阻率变化量分别与图5～6中的实验数据[16]进行比较。结果表明本研究得出的结果与环状流(高Vsg)中的实验数据拟合度较好。

表1基于平均绝对百分比误差与标准差对比fMDp和fMDAL

项目平均绝对百分比误差标准差fMDAL0.1030.09fMDp0.0620.089

图4随fMDE增大的fMDp与fMDAL的对比

a)Vsl=0.1 m/s,D=0.012 7 m

b)Vsl=0.4 m/s,D=0.012 7 m

c)Vsl=0.104 m/s,D=0.025 4 m

d)Vsl=0.125 m/s,D=0.025 4 m

图6 当Vsg=38 m/s,D=0.012 7 m时,对比不同液体流速(Vsl)下的DR估算值与实验数据

3 结论

1)针对加入聚合物型减阻剂的环状流,通过对已发布的实验数据使用量纲分析和曲线拟合,推导了预测其摩阻系数的新显式方程,该方程基于边界层的对数速度分布和幂律分布,计算结果与实验数据对比表明两者的拟合度较好。

2)比较本文计算结果和Al-Sarkhi的计算结果,可知fMDp和fMDE之间的拟合度要好于fMDAL和fMDE。针对环状流(高流速),将对应于气体表面流速Vsg的减阻率DR变化量与实验数据进行比较,本文计算结果与实验数据之间的拟合度较好,并且减阻率DR随着气体表面流速Vsg的增加而逐渐减小，新显式方程可用于准确预测环状流摩阻系数，有助于加强对管道输送能力的控制。