基于UKF的大失准角船舶行进间对准技术研究

裴新凯 ，张吉先 ，郭玉胜 ，丁海旭 ，庄广琛 ，邓 亮

(1.北京自动化控制设备研究所，北京 100074；2.昆明海威机电技术研究所，昆明 650200)

0 引言

捷联惯导系统(Strapdown inertial navigation system，SINS)具有完全自主性的优点，但误差随时间积累,而全球定位系统(Global Positioning System，GPS)误差不随时间积累,但不具备自主性，二者优势互补。因此，常构造SINS/GPS作为组合导航系统，其中初始对准是保证导航精度的关键技术。目前，误差传播模型和滤波算法是研究捷联惯导系统初始对准的2个重要问题，而描述SINS的误差模型本质上是非线性的，标准卡尔曼滤波(Kalman Filter，KF)只能有效解决小失准角下的初始对准问题，工程上通常先用双矢量定姿原理进行粗对准[1-2]，在小角度下应用标准卡尔曼滤波。本文提出了应用无迹卡尔曼滤波(Unscented Kalman Filter，UKF)的方法，在未知角度的前提下直接进行滤波，估计出满足导航精度的初始姿态信息。

UKF和标准卡尔曼滤波都属于线性最小方差估计，算法都是基于模型的[3-5]；区别在于标准卡尔曼滤波的均值和方差具有线性传递性，可以通过递推直接进行计算，但只适用于系统方程和量测方程均为线性的情况。尽管扩展卡尔曼滤波(Extended Kalman Filter，EKF)可解决系统和量测为非线性时的估计问题，但必须对原系统和量测作泰勒级数展开，并保留线性项，本质上与KF没有区别，因此，EKF只适用于弱非线性对象的估计[6]。对于捷联惯导系统拥有维数较高的状态变量，通过线性化求解雅格比矩阵比较复杂，而UKF通过无损变换(Unscented Transform，UT)，舍弃近似非线性函数转而近似其函数的概率密度分布，可以有效解决大失准角条件下的估计问题。本文通过建立捷联惯导系统的非线性误差方程[4,7-8]，设计UKF滤波器，以GPS的速度信息为观测量，实现大失准角条件下的行进间初始对准。同时由于GPS天线的安装位置与惯导位置间存在杆臂误差，杆臂越长、转弯角速度越大，速度测量误差就越大，进而影响对准精度。本文对载车的杆臂效应作了简要分析后，建立了包含杆臂参数的UKF模型，以实时地对杆臂大小进行估计[9-11],最后通过实验验证了算法的有效性。

1 SINS/GPS组合导航系统非线性误差模型

1.1 SINS姿态误差方程

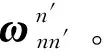
(1)

其中：

(2)

(3)

1.2 SINS速度误差方程

理想情况下：

(4)

实际系统中：

(5)

式中

(6)

式(4)和式(5)作差得：

(7)

1.3 SINS位置误差方程

纬度误差方程为：

(8)

经度误差方程为：

δLvetanLsecL/(RN+h)

(9)

1.4 杆臂误差方程

假设GPS天线相对惯导位置在载体系下可以表示为：

δl=[δlx,δly,δlz]T

(10)

由图1可知，当载体发生角运动时，2个测量点速度的关系为：

(11)

式中，右边第二项就是由杆臂引起的速度误差，其中：

(12)

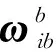
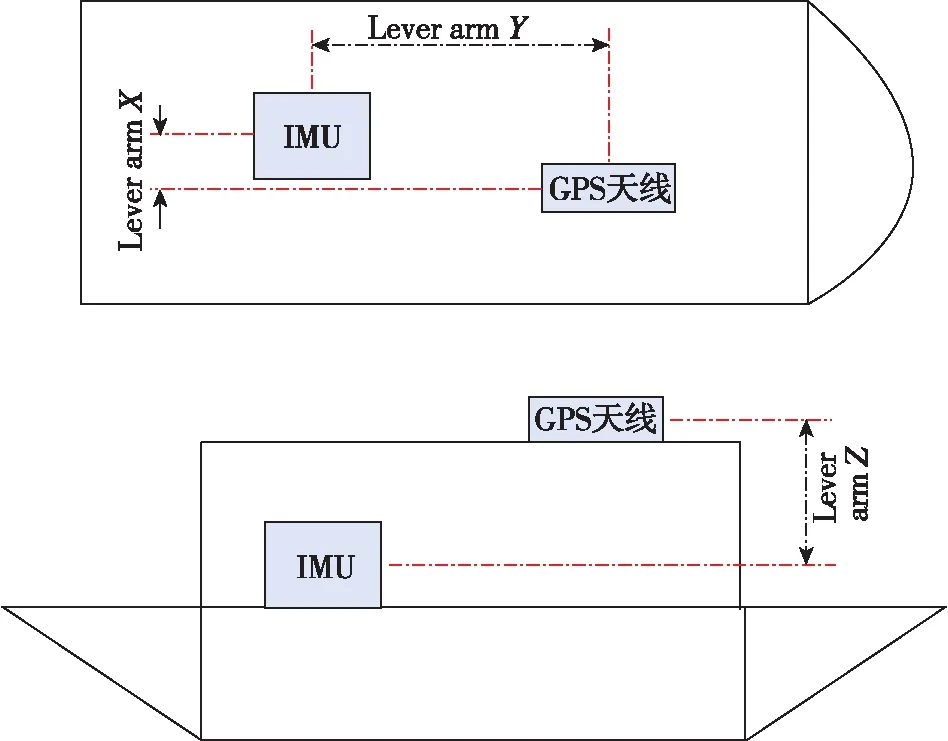
图1 IMU安装位置与天线安装位置关系Fig.1 Relative position of IMU and antenna installation

2 UKF算法

一般滤波模型描述如下

(13)

UKF采用与KF一样的算法结构，所不同的是，在KF中可直接通过线性方程确定状态统计量的转移，而UKF不行，后者必须借助UT计算采样点来演化状态分布特性的转移[13-14]。

2.1 UT

UT以两条准则为基础：1)对单一点执行非线性变换是容易的(相比与整个概率分布函数)；2)在状态空间中不难找到一组点，利用这些点可以近似状态向量的真实概率分布函数。

一般意义下的UT算法框架如下：

2)对采样的输入变量Sigma点集{χi}中的每个Sigma点进行f(·)非线性变换，得到变换后的Sigma点集{yi}。

yi=f(χi)

(14)

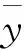
(15)

(16)

2.2 适用于SINS/GPS组合导航系统的UKF算法

为了减少计算量和保证UKF的稳定性，在大失准角的条件下并未将惯性器件误差纳入滤波方程，因此，滤波状态为

x=[φE,φN,φU,δvE,δvN,δvU,δL,δλ,δlx,δly,δlz]

则UKF的状态方程可写为如下的离散形式：

(17)

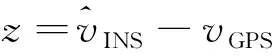
z(k)=Hx(k)

(18)

由此可见，系统的状态方程为非线性的，而观测方程为线性的，所以可以对观测方程的更新进行化简。按对称采样方法选取2n+1个Sigma点近似系统状态的先验统计特性[15-16]。

1)初始化状态变量及其均方差

(19)

2)时间更新

(20)

χi,k+1|k=f(χi,k)

(21)

(22)

(23)

(24)

3)量测更新

Pzz=HPk+1|kHT+R

(25)

Pxz=Pk+1|kHT

(26)

(27)

(28)

(29)

(30)

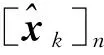
λ=α2(n+κ)-n

(31)

(32)

(33)

(34)

(35)

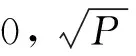
3 试验与分析

3.1 仿真分析

首先设计轨迹发生器，运行轨迹如图2所示，初始速度为2m/s，仿真时间773s。初始失准角为俯仰角10°，滚转角10°，航向角80°。采样周期为10ms，陀螺漂移0.01(°)/h，加表零位50μg。

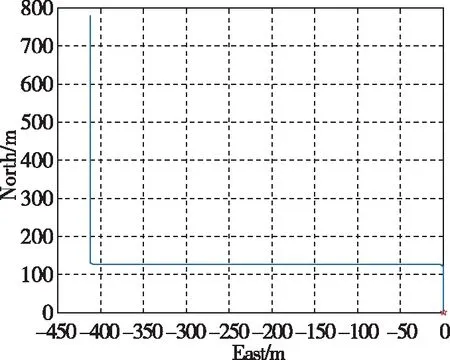
图2 仿真运动轨迹Fig.2 Simulation trajectory

杆臂设置为[2m,3m,5m]，在50s以后船体向左转弯90°，250s后再向右转弯90°，转速均为10(°)/s，在500s之后船体有3次滚转的机动，转速为10(°)/s。

分别进行没有杆臂补偿和有杆臂补偿的UKF对准仿真，对二者进行比较，由图3和图4可以看出，利用UKF进行行进间初始对准，可以有效地估计出误差失准角。通过对杆臂进行建模，在UKF过程中对参考速度误差进行分解，可以有效地解决杆臂误差造成的影响。

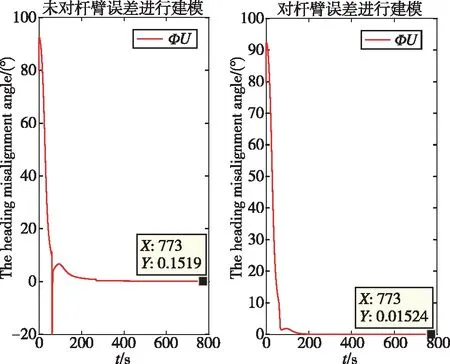
图3 有无杆臂模型的天向失准角对比Fig.3 Comparison of the upside misalignment angles with or without the lever arm model

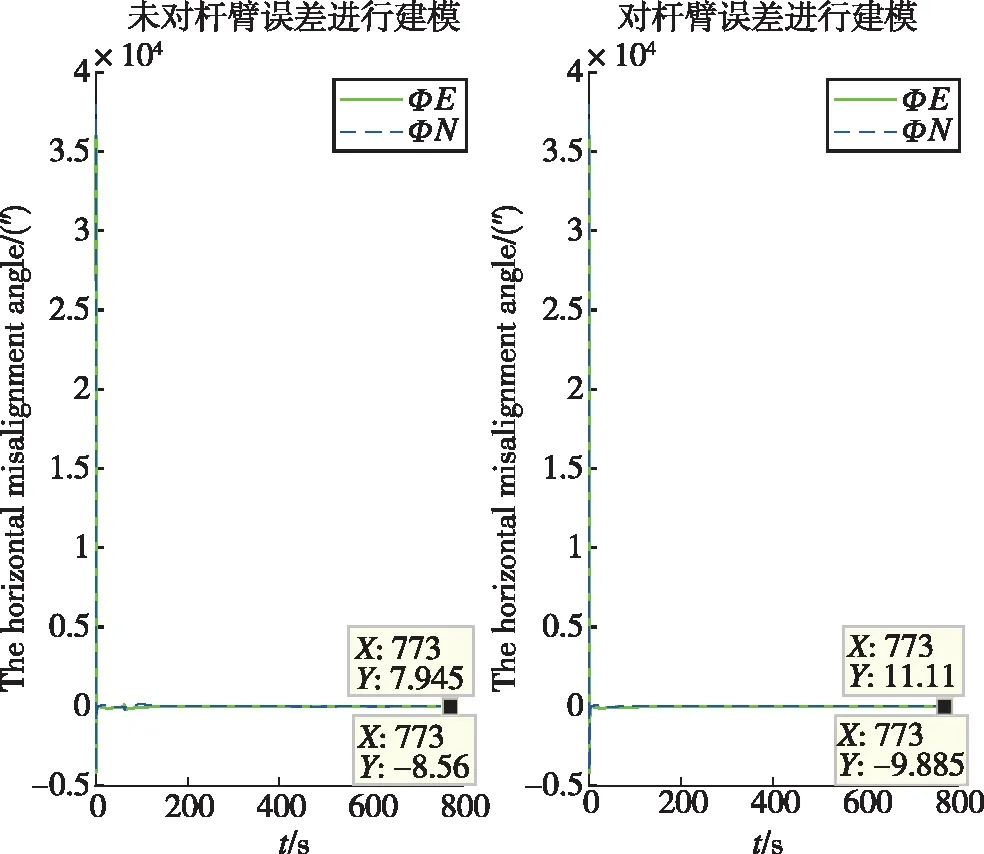
图4 有无杆臂模型的水平失准角对比Fig.4 Comparison of the horizontal misalignment angles with or without the lever arm model

如表1所示，在对准结束时刻，对杆臂误差进行建模后的初始对准航向精度要比没有对杆臂建模的航向精度高出1个数量级。

表1 补偿杆臂前后的失准角对比Tab.1 Comparison of misalignment angle with or without lever arm compensation

从图5可以看出，该方法能够估计出3个方向上的杆臂误差，在2次转弯过程中，水平方向的杆臂误差均有明显修正效果，通过P阵的曲线变化也可以得到同样的结论，如图6所示。该仿真结果表明，利用UKF可以解决导航初始时刻的大失准角问题，同时补偿了杆臂误差导致的对准精度低的问题。

图5 杆臂估计值Fig.5 Estimated value of lever arm

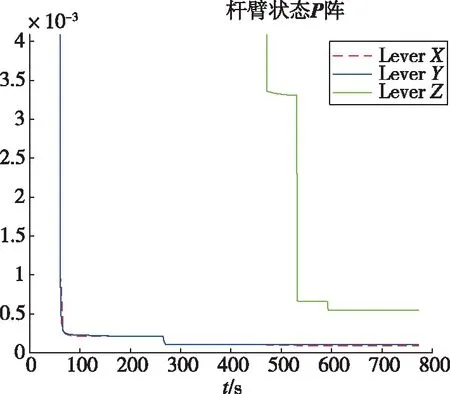
图6 杆臂状态的P阵曲线Fig.6 P-array curve of the lever arm state

3.2 海试试验数据验证

利用在青岛某海域的SINS/GPS组合导航试验数据对算法进行进一步的验证。图7展示了实验用船与调试现场。

图7 船载试验用船及各设备安装图Fig.7 Shipboard test ship and equipment installation

海试过程为粗对准5min，然后船舶进行转弯运动精对准30min，最后转组合导航。为了便于进行基于惯性系的粗对准和UKF对准算法的比较，截取精对准之后时刻的IMU和GPS数据，分别用UKF和基于惯性系算法进行动基座初始对准。因为此时弹上数据已经经过滤波修正，因此可以当作基准。从图8、图9可以看出，二者的水平姿态角对准结果基本相同，根据表2可以看出，补偿了杆臂的UKF算法航向角收敛速度较快，航向精度也较高，200s时的航向对准精度优于传统对准算法，可达到0.03°。图10展示了当粗对准结束后转KF经过几次航向机动后的滤波效果，UKF的主要目的是降低失准角误差，可以看出当失准角比较小以后，采用经典卡尔曼滤波更加有效。

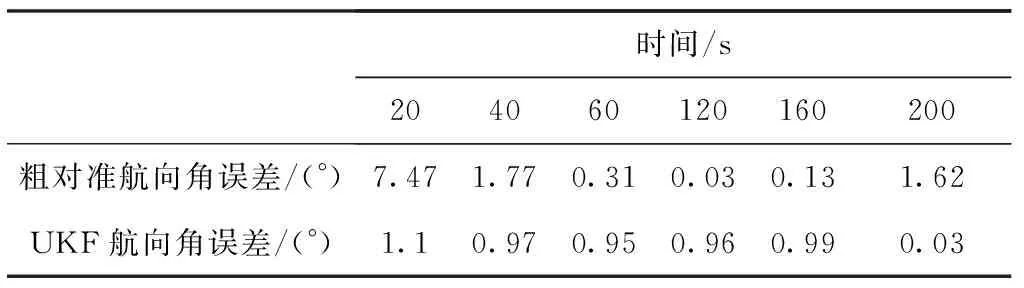
表2 航向角误差值对比Tab.2 Comparison of heading angle error

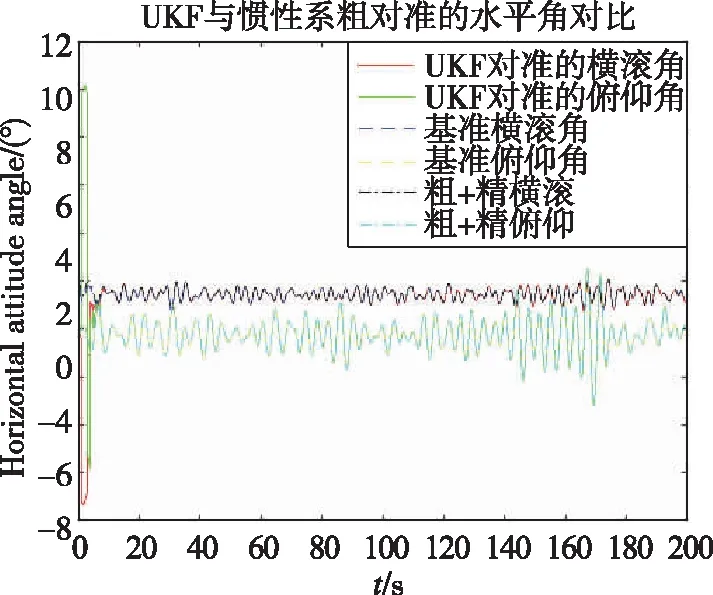
图8 UKF与粗对准+KF精对准水平姿态角对比Fig.8 Horizontal attitude comparison of UKF and KF with coarse alignment

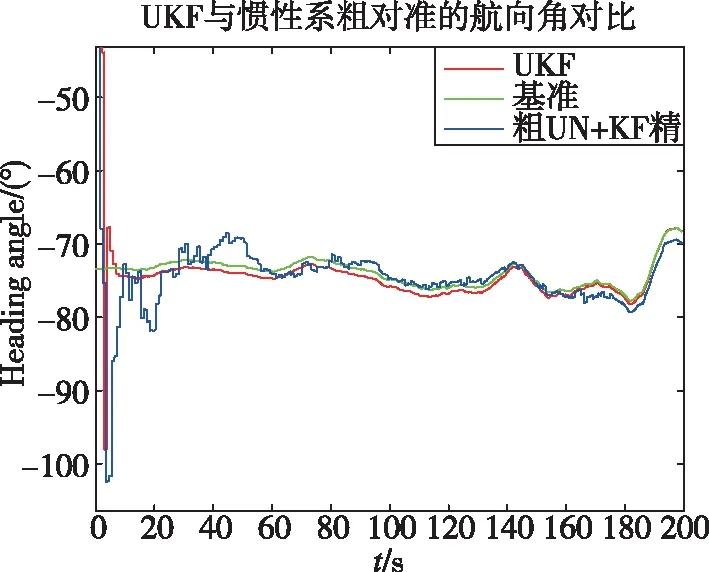
图9 UKF与粗对准+KF精对准航向角对比Fig.9 Heading angle comparison of UKF and KF with coarse alignment

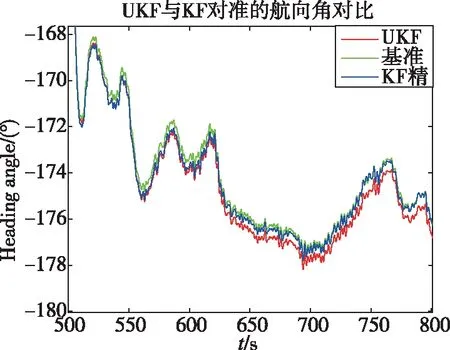
图10 UKF与KF精对准航向角对比Fig.10 Heading angle comparison of UKF and KF alignment

4 结论

针对船舶动基座过程中的大失准角初始对准问题，提出了一种简化的UKF算法，通过对GPS杆臂进行建模，相当于对不准确的参考速度信息进行补偿。通过仿真分析和海试试验结果表明，基于UKF的行进间对准算法可以有效地解决组合导航过程中初始大失准角的问题，并且精度优于传统粗对准方法。后续将对UT作进一步分析，简化状态方程中线性部分的计算方法，提高计算效率，进而对状态方程进行扩展，提高计算精度。