一种基于无线信号辅助的室内无死角定位算法

刘 宇，李俊林，路永乐，张 旭，方 针

(1.重庆邮电大学光电信息感测与传输技术重庆市重点实验室,重庆 400065；2.中国电子科技集团公司第二十六研究所,重庆 400065)

0 引言

室内定位技术发展已久，但常用的WIFI、蓝牙、射频等基于信标的室内定位技术均需预先部署大量的基础设施且定位精度受环境所限[1]，而惯性导航定位技术不受外界环境所限制，在室内定位中有着天然的优势，但存在累计误差大的缺点[2]。因此，目前还没有某种单一的室内定位技术能够提供精确、稳健和一致的定位与跟踪服务[3]。所以采用各种辅助方式增强惯导系统的实用性，实现室内无死角定位是当前的研究热点。

国内外许多研究人员对该技术已经开展了大量的研究工作。刘春燕等[4]提出了一种自适应模型噪声的扩展卡尔曼滤波(Extended Kalman Filter,EKF)算法，实现行人航位推算(Pedestrian Dead Reckoning，PDR)与WIFI定位源的滤波融合，有效抑制了惯性定位误差的累积，将整体误差控制在5m左右。Chen P等[5]使用卡尔曼滤波对惯性定位和超带宽(Ultra Wideband，UWB)定位数据进行融合，得到的融合定位系统精度高，实时性能好；Zou Han等[6]基于手机传感器将WIFI与PDR融合，并采用新兴的iBeacon技术矫正WIFI覆盖盲区的PDR漂移误差，采用粒子滤波(Particle Filter，PF)融合得到的定位精度可以达到亚米级，但两者均局限于二维定位。周宝定等[7]通过智能手机内置的传感器获取用户行为感知来辅助进行室内行人定位，以消除PDR的累积误差；Liu Mengyun等[7]在智能手机上利用视觉、WIFI和惯导来实现多源室内无缝定位，95%的几率可以达到1.32m的定位精度。王敬贤等[8]采用手机自身光、磁、惯性传感器模块和卫星模块进行组合，实现行人室内外无缝导航，避免了导航过程中路径中断现象的产生。中国矿业大学等高校的学者们在相关课题的支持下，进行了基于智能终端平台的以WIFI和惯性导航系统(Inertial Navigation System，INS)为主的室内无缝定位技术研究[9-14]，如Li Xin等[15]融合了蓝牙和PDR技术，在不增加基础设施的情况下提供米级室内定位精度，但同样地，该机构的研究结果都是基于二维空间实验得出的。

上述国内外研究机构及研究学者的努力都有很大收获，提高了系统定位精度或稳定性，极大地促进了无缝定位技术的发展,但无须昂贵的基础设施定位系统，如智能手机终端受传感器精度限制总体定位精度不高，而能实现高精度定位的定位系统硬件开销较大，系统的普及性差，且大部分处于二维空间定位的研究。本文提出了一种基于WIFI信号辅助的室内定位算法，以惯性定位为主导，采用WIFI信号进行位置和航向的修正，能够利用现有的无线路由器，减少部署开销，提高惯性定位的精度，便携高效地实现室内无死角定位。

1 系统架构

本文实验采用实验室自主研发的微惯性测量单元(Micro Inertial Measurement Unit，MIMU)，内部集成了陀螺仪等传感器和ESP8266。在数据采集过程中将其佩戴在测试人员腰部脊椎位置，载体坐标系即微惯性测量单元坐标的定义如图1所示，X轴正向向右，Y轴正向指向前进方向，Z轴正向垂直地面向上。实验中数据采集频率设定为50Hz，输出数据保存在笔记本电脑上。

图1 微惯性测量单元坐标定义Fig.1 Definition of MIMU coordinate

本文算法首先利用了微惯性测量单元中的陀螺仪、加速度计、磁力计和气压计四种传感器实现三维的惯导定位。然后利用无线信号对行人的位置和航向进行纠正，实现室内无死角定位。算法框图如图2所示。

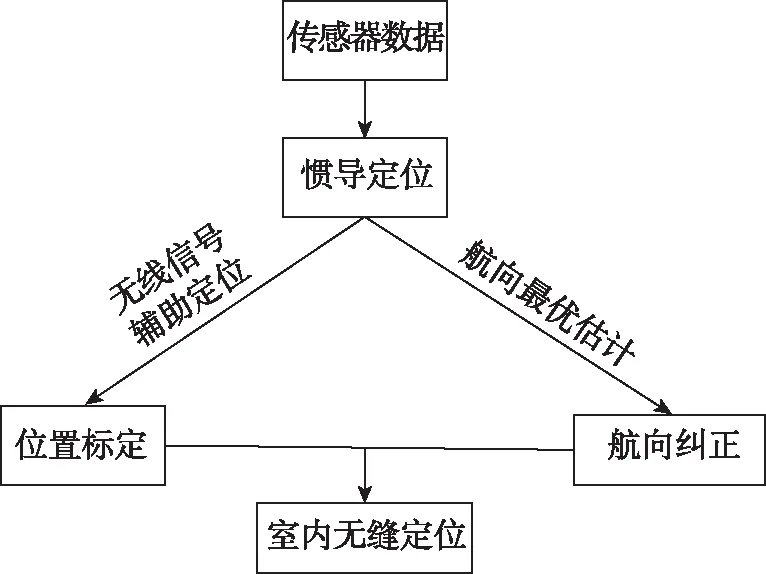
图2 算法框图Fig.2 Algorithm block diagram

2 无线信号辅助定位算法

目前，大量室内建筑都广泛布设了WIFI无线路由器，众所周知无线信号的强弱与距离信号发射端的远近有关。若提前知道无线访问接入点(Access Point,AP)的物理位置，则完全可以利用这些信息进行无线信号辅助惯导定位，实时纠正INS定位的位置，消除位置上的累计误差，增强INS的适用性。

为了实际应用操作简单，本文不考虑根据计算传播损耗模型公式进行接收功率与距离之间的转化，而是直接进行实验测试来得出接收信号强度指示(Received Signal Strength Indicator，RSSI)与距离的对应关系。在室内活动过程中，行人佩戴的定位终端会检测到附近的无线AP发射出的信号，信号强度通常处于-110～-20dBm区间。实际中，一般把-90dBm看成临界值，若检测到比-90dBm还低的信号强度值，则判定此时无信号；上限以-20dBm为临界值，凡是高于-20dBm则认为信号极好，判定其所处位置应该在AP附近。设置AP的RSSI功率辐射值为10dBm，分别在距离AP1m、2m、3m、4m、5m、6m、7m、8m、9m、10m的位置处采集无线信号30次，统计每个位置上的RSSI的最大值、最小值和平均值。最后得到RSSI与距离的变化特性如图3所示。

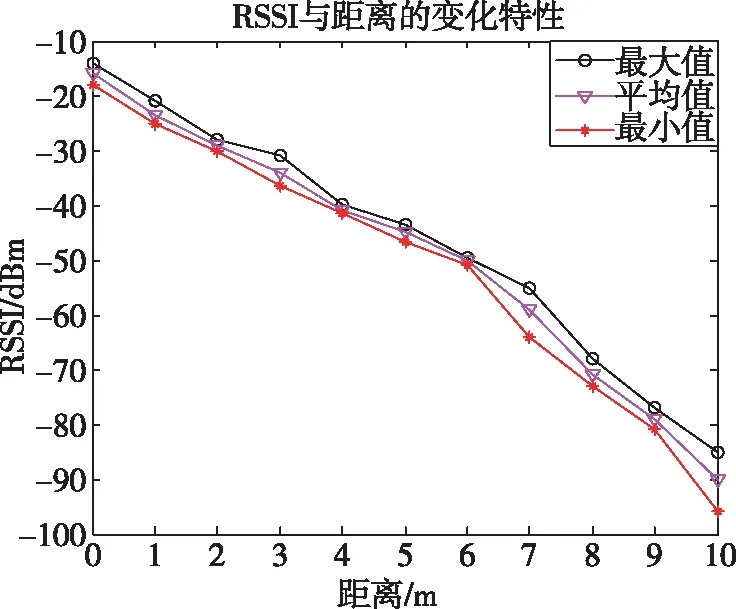
图3 RSSI与距离的变化特性Fig.3 Characteristics of RSSI-distance variation

从图3可以明显地看出，RSSI的平均值随着定位终端与AP间的距离的增加而递减。具体地，当RSSI在-10～-20dBm范围内时，定位终端与AP的距离不超过1m；当RSSI在-20～-25dBm的范围内时，定位终端与AP的距离在1～2m之间。随着2个端点之间距离的增大，会出现RSSI数值大幅度变化的情况，说明RSSI与位置之间只在距离较短时才存在较好的对应关系，当距离逐渐增大后，这种对应关系将变得不再可靠，此时采集的RSSI无法用于辅助定位。

根据上述特性，设置定位终端接收到的信号强度阈值RTh为-6dBm，当定位终端接收到的某个AP的RSSI超过设定阈值RTh，就可推算出行人处于距离该AP半径为1m的单位圆内，就将行人当前位置更新为已知的该AP的物理位置。无线信号辅助矫正实时位置方法如图4所示，INS由于长时间误差累计，对行人的实时定位出现明显偏差，当行人佩戴定位终端经过某AP时，就通过阈值法将实时位置更新为已知的该AP的物理位置，而且由所设的阈值和距离之间的对应关系可知，真实位置与校正位置之间的误差小于1m，满足室内定位精度的需求。

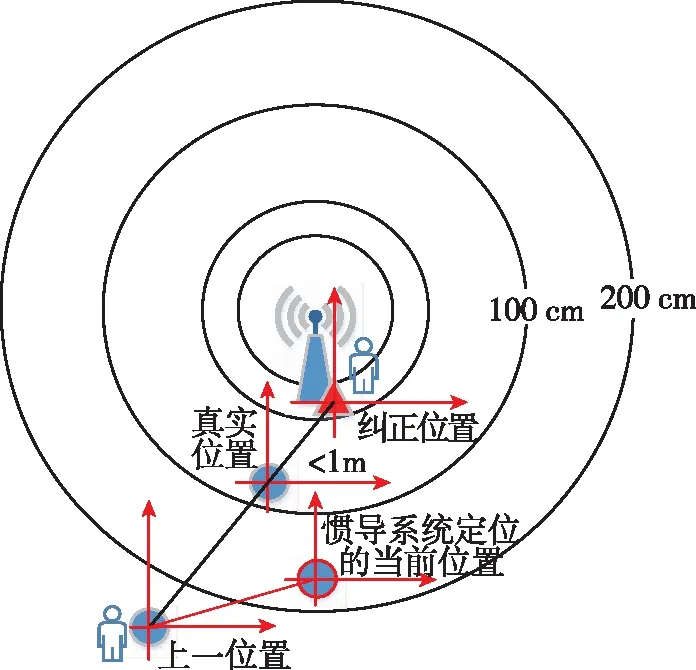
图4 无线信号辅助矫正实时位置示意图Fig.4 Schematic diagram of wireless signal assisted correction for real-time location

3 航向最优估计算法

3.1 基于陀螺增量的航向优化算法

定位终端佩戴在行人腰部，并不是完全固定不动的，因此，正常行走过程中终端随人体运动带来的抖动误差都会在航向上有所表现。根据多次的仿真分析，这种航向误差在一般在5°～10°，随着本来的误差累积，将会对最终的定位精度造成极大的影响。为了抑制这种航向误差带来的不良影响，本文提出了利用角速率变化量进行航向误差的修正。

受限于目前建筑物的规则矩形结构，整个室内无死角定位过程中，将行人的正常行走分为两种情况：1)直线行走，航向基本保持一致；2)转向行走，航向发生剧烈变化，所以对航向误差的修正也是从这两方面进行考虑。刚好在INS中，使用陀螺仪进行姿态解算，动态响应良好，短期内精度高，但漂移会因长时间工作而逐渐变大，使用加速度计和磁力计组合进行解算，静态解算时精度高，而动态解算时由于加速度计的动态误差而导致精度降低，即可利用这两种不同的姿态解算组合的优点来对两种行走情况的航向误差做补偿。

若是行人航向发生剧烈改变，仍旧利用EKF融合算法进行解算，将载体坐标转换中的四元数Q作为状态矢量，将测量的三轴加速度计值和三轴磁力计值分别进行归一化，得到ak和mk，作为观测量，构建卡尔曼滤波方程，如式(1)：

(1)

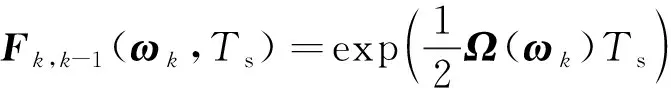
最后，通过更新后的四元数(q0,q1,q2,q3)，得到目标航向角：

(2)

若是行人航向未发生变化，即基本保持直线行走，但存在抖动误差，则需要对航向进行优化处理。其中关键是要对行人是否发生剧烈的航向变化进行判别，本文以陀螺短时积分为依据，通过阈值法进行判断。若是陀螺积分大于设定阈值，则认为此时航向发生剧烈变化，不需要进行航向误差补偿；若是陀螺积分小于设定阈值，则对误差进行修正。

一般当行人直线行走时，定位终端会随人体运动发生轻微的移位。陀螺仪良好的动态性能对这种极小幅度的摆动也会作出响应，直接体现在EKF求解的航向角上会有10°左右的误差波动。本文选择滑动均值滤波进行误差处理，具体措施为，在用陀螺积分作阈值判断航向变化时，若判定行人航向未发生剧烈变化或变化较小，且持续一段时间Δh，则判定行人处于平稳行走状态，使用该平稳时间区间内的航向均值代替当前航向作为行人运动的前进方向；若是行人航向发生了剧烈变化，则不做滤波处理，等待下一个平稳状态的出现。综上，整个航向优化的具体流程如图5所示。

图5 航向优化流程Fig.5 Heading optimization process

图6所示为航向优化算法修正前后的航向对比图。从图中可以看出，航向改变时，EKF准确地解算出航向角，符合实际情况；而当航向未发生改变，即保持平稳运动状态时，优化后的航向更为平滑，减小了腰部抖动误差对航向的影响。

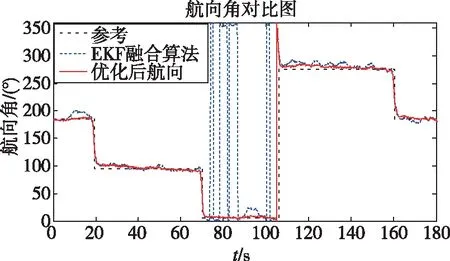
图6 航向优化前后对比图Fig.6 Comparison of heading angle before and after optimization

3.2 在线实时航向纠正

航向误差产生的根本原因在于陀螺仪长时间工作会产生较大的漂移，这也是惯导系统最根本的误差所在。当通过INS定位得到的位置出现了偏差时，一般是距离和方向两方面的误差累积所导致的。

同样地，可以利用已知物理位置的无线路由器及其所处位置的建筑物几何结构信息进行实时的航向纠正。目前，室内建筑大部分是规则的矩形结构，所以一般AP的安装位置不外乎直线走廊和拐角两处。凡是路过AP进行了位置矫正，那么一定是从走廊的左右两边或者拐角的两边朝AP靠近，所以就算解算的航向角出现误差，却可以根据无线信号辅助定位的位置纠正点确定行人行走过程中的真实航向，完成航向误差的实时纠正。

以无线节点被装置在狭长的走廊上为例，行人经过该AP被纠正了定位位置，行走方向受走廊地理条件限制，只能是沿走廊从AP的右边或者左边走过来，如图7所示。用Hright表示从AP右边走过来的方向，用Hleft表示从AP左边走过来的方向。AP在导航坐标系下的物理位置已知，那么方向Hright和Hleft在导航坐标系中的具体角度也是确定的。接下来只需判断行人是从左边还是右边路过的该AP，即可确定行人的实际航向。虽然惯导长时间工作航向会有偏差，但该偏差是一步一步发散的，所以可以根据短时间内的平均航向和该已知AP的左右2个方向做差值，比较判断行人行走方向，表示如下：

(3)

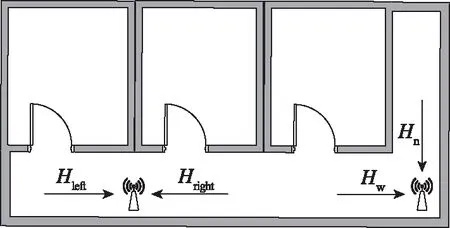
图7 行人经过AP行走方向示意图Fig.7 Schematic diagram of pedestrians walking through the AP

当无线路由器被装置在走廊的拐角处，判别方法仍沿用上述的阈值法。

将矫正后的航向信息输入到EKF中进行下一步迭代，即可有效地消除惯导累计误差。

在已知无线路由器位置的前提下，利用无线信号辅助矫正位置和航向进行在线调整后，不仅提高了定位精度，更清空了惯导的累计误差，相当于对传感器件进行了初始化，提高了定位系统的定位时间，增强了惯导系统的实用性。

4 实验验证

为验证本文提出的室内无死角定位算法的可行性与可靠性，本文采用实验室自主研发的微惯性测量单元进行实验验证，该测量单元内部集成1个三轴加速度计、1个三轴磁力计、3个单轴陀螺及1个微处理器。其输出的横滚角和俯仰角的动态精度为0.5°，航向角的动态精度为3.0°，加速度量程为50m/s2。

选择重庆邮电大学第一教学楼作为实验测试环境，图8所示为第一教学楼的楼层结构图及无线路由器的布点方案。蓝色的无线路由器代表实际的无线信号发射端，AP2表示布置在2楼左边走廊的无线路由，AP3表示布置在3楼中间走廊的无线路由，AP4表示布置在4楼右边走廊拐角的无线路由。中间的走廊行走距离为50m，图示右边走廊行走距离为18m，左边走廊行走距离为22m，楼梯长度10m左右。

图8 第一教学楼平面图及测试路线Fig.8 Floor plan of the 1st teaching building and test route

测试人员腰部佩戴定位终端从1楼起点出发，沿路线每层楼上下重复行走，如此循环至少行走30min回到1楼起点，分别在没有无线信号和有无线信号两种情况下行走，即对纯惯导定位算法和本文提出的室内无死角定位算法进行测试。纯惯导航迹推算得到的定位结果和本文提出的室内无死角定位算法得到的定位结果分别如图9和10所示。从图中可以看出，随着时间的推移，纯惯导定位出现明显的航向漂移，而本文提出的室内无死角定位算法仍然一直提供着精准定位，航向漂移极小。可见本文提出的室内无死角定位算法可在室内提供长期有效的三维定位信息。

图9 纯惯导定位结果Fig.9 Results of the inertial navigation

图10 本文提出的室内无死角定位结果Fig.10 Results of the proposed indoor no-dead-space positioning

根据实验统计，测试人员沿着一教行走至少30min后回到起点，能达到楼内(2楼走到4楼又回到2楼)重复行走5次，整个行走距离大约2100m。记录纯惯导定位和本文提出的室内无死角定位两种算法的定位参数，统计结果如表1所示。由表1可知，纯惯导技术定位过程中航向出现漂移，航向误差达到35.61°，水平距离误差高达36.01m，定位误差为1.73%；而使用无线信号辅助的室内无死角定位整个测试过程无轨迹发散迹象，最终航向误差为9.97°，水平距离误差为12.57m，定位误差为0.61%，明显小于纯惯导定位误差，证明了本文研究的室内无死角定位技术与纯惯性传感器定位技术相比，能够提供更持久和准确的位置信息。

表1 纯惯导和本文提出的室内无死角定位实验结果对比表Tab.1 Comparison of pure inertial navigation and the proposed indoor no-dead-space positioning based on wireless signal aided location experimental results

为了测试室内无缝定位算法的稳定性，首先对多次实验下的系统定位精度进行了评估，选择10位测试人员仍然按照上述路线行走，同样要求至少行走30min后，回到出发点，行走距离大约2100m。一般地，惯导的定位效果主要是看闭环行走起点和终点的距离偏差与实际行走距离的误差比。统计测试人员回到原点后的观测结果，计算出垂直误差、水平误差、航向误差、闭环误差等，结果如表2所示。

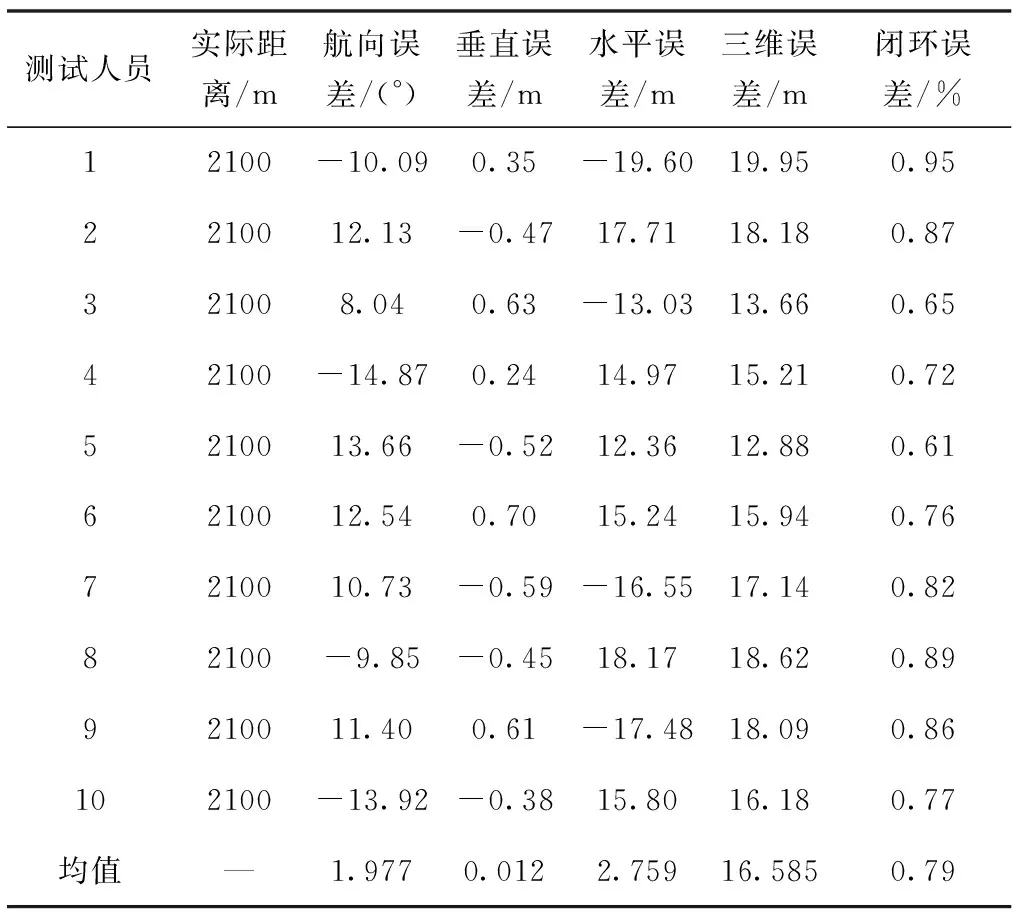
表2 三维定位测试结果Tab.2 3D positioning test results

从表2中可以看出，实验目标距离为2100m，起点与终点的最大三维距离误差为19.95m，最大闭环误差为0.95%，平均闭环误差为0.79%。所以本文所研究的室内无死角定位算法的闭环误差小于1%，满足室内的定位精度需求。而且10位测试人员通过上位机得到的定位结果均与实际行走轨迹相似，航向角漂移较小，保持在15°以内，并未出现传统惯导普遍存在的明显航向漂移与轨迹发散的情况，以上多次实验测试证明了该算法的稳定性。

然后选择图书馆、信息科技大厦和第四教学楼三种不同于第一教学楼的室内环境进行实验测试。每种测试场景中都规定起始点，并根据不同室内建筑物的几何构造，进行不一样的AP布点方案，每种环境下测试20次，每次测试依旧不少于30min，统计每个环境下的定位闭环误差，结果如表3所示。测试结果表明，不同室内环境下的平均误差与0.79%相比，偏移均在±5%以内，多次测试的数据标准差较小，证明了该算法具有较高的稳定性，可以稳健地实现室内无死角定位。

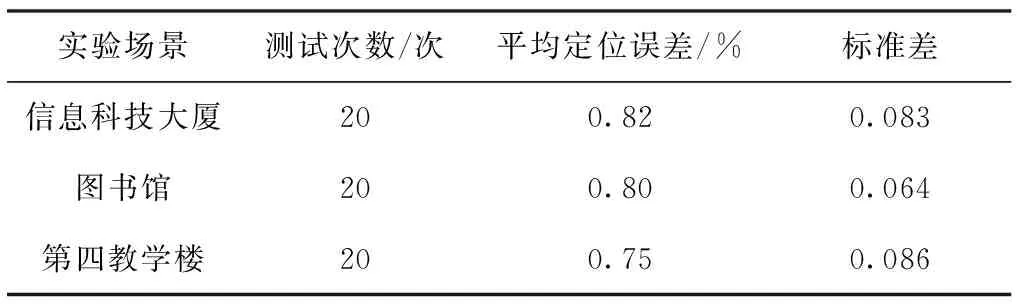
表3 不同应用场景测试结果Tab.3 Different application scenarios test results

通过同一室内定位场景的多次重复性三维定位实验测试，本文提出的室内无死角定位算法定位误差小于1%，再通过不同室内定位场景的多次重复性实验测试，平均定位误差偏移不超过±5%，证明了本文算法的可靠性。因此，验证了本文提出的使用无线信号辅助的室内无死角定位算法的可行性与可靠性。

5 结论

针对纯惯性导航系统累计误差大、无法长时间工作的问题，本文提出了一种利用无线信号辅助定位的室内无死角定位算法。该算法利用无线信号对惯导定位的位置进行实时的标定，然后针对不同的运动状态，对无信号时的航向做平滑处理，再利用无线信号对航向进行实时地纠正，从位置和航向两方面消除惯导的累积误差，提高定位精度。通过实验证明，与纯惯导定位技术相比，本文提出的室内无死角定位算法定位精度更高，可靠性更好，进一步提高了惯性导航定位技术的实用价值。