3.2均值不等式（一）教学设计

辽宁省抚顺德才高级中学 郭志衡

教学目标：

1.探索并了解均值定理的证明过程.

2.会用均值定理解决简单的最大值，最小值问题.

学习重点：

了解均值定理的证明过程并会用其解决简单的求最值问题.

学习难点：

均值定理证明过程和等号成立的条件.

教材分析：

均值不等式又称基本不等式，选自普通高中课程标准实验教科书（人教B版）必修五第三章第2节内容，是不等式这一章的核心，也在高中数学中有着比较重要的地位。对于不等式的证明及利用均值定理求最值等实际问题中起到工具作用。通过本节的学习有利于学生对后面选修内容不等式的证明和前面函数内容的一些最值值域进一步研究，起到承上启下的作用。

学情分析：

均值定理作为高中最基本的不等式要求学生必须掌握，难度不大。学生的逻辑思维能力稍弱，讲解证明时可能存在问题，要注意引导。但学生的模仿能力很强，对于直接用公式解决的问题掌握起来很快，做题时要注意特殊地方的强调。

课型：

新授课

教学准备：

PPT，学案

教学方法：

启发讲授法，问题教学法，小组讨论法。

教学过程：

一、复习引入思考：x、y是任意两个实数，请用合适的符号填空。1、______0 2、()2 x−y Q1：请回答出三个式子所填符号并回答出什么情况下等号成立。（2分钟）_______0 3、x y xy 2 2 2+ −x+y2 2______xy二、新知探究均值定理如果2 a b R+∈,，那么a b ab+ ≥2，当且仅当a=b时等号成立。证明：方法（1）作差法+a b ab a a b b a b 1()2 0 2 2 2−= −·+ = − ≥■2 2()1■2■■()通过思考提问，推导出均值定理内容（1.5分钟）Q2：我们怎么证明这个不等式成立那？（同桌讨论3分钟）展示小组讨论结果，由于孩子们提前进行了预习，所以大概思路应该会有。（3分钟）当且仅当 ，即a=b时，等号成立.证明：方法（2）几何法如下图，以长为a+b的线段为直径作圆O，在直径AB上a= bQ3：请在图中找出能够代表a+b 和ab 的取点C，使AC=a,CB=b，过点C作垂直于直径AB的弦DD'.能否借助该几何图形解释均值不等式的几何意义？线段长度？2解: 由题意，ΔABD是直角三角形，则由射影定理得CD2=CA·CB，即CD=ab ，连接OD，则OD +=ab，当且仅当点C与圆心O重合，即a=b时，不等式中的等号成立.所以均值不等式的几何意义为：圆的半径不小于半弦.三、典例解析例1.已知ab＞0，求证：，显然，圆O的半径OD不小于半弦CD，a b ab+ ≥2即2，并推导出式中等号成立的条件.证明：∵ab＞0∴+ ≥2 b a a b b a a b＞ ＞0, 0 b a b a a b a b，根据均值不等式，得+≥ ·=2 2.当且仅当 ，即a=b时式中等号成立.例2.求函数的值域.解：（1）当x＞0，则b a a b=，当且仅当x=1是等号成立，此时值域为1 0 x＞ ，原式y x x x x=+≥ ·=1 1 2 2[ )2,+∞（5分钟）师生齐读均值定理的内容，老师引导学生概括均值定理应用条件。Q4：为了方便记忆深化理解，请同学们尝试用几个字概括均值定理？（3分钟）Q5：思考一分钟，结合均值定理找一名同学阐述你的解题思路？（4分钟）教师强调均值定理取等条件的求法。Q6：:请大家思考两分钟时间，然后举手回答你对本题的见解？（3分钟）（4分钟）（2）当x＜0，则− ＞ − ＞x x 0, 0 1■，则 − +− ≥ − ·− =■■■1 1■x ()()2()()2 x ■x x

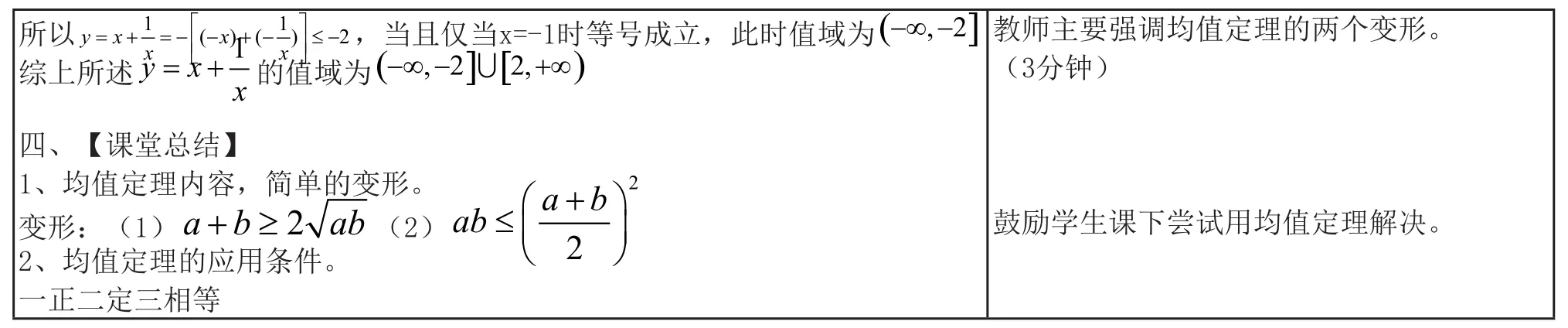
所以= + =− − +− ≤−■y x x x 1■1■ ，当且仅当x=-1时等号成立，此时值域为()()2 1■(]−∞−,2综上所述y x x=+■的值域为x ■(][ )−∞ − ∪ +∞,2 2,教师主要强调均值定理的两个变形。（3分钟）四、【课堂总结】1、均值定理内容，简单的变形。变形：（1）2 a b ab+ ≥2（2）ab +■ ■≤■ ■■ ■a b 鼓励学生课下尝试用均值定理解决。2、均值定理的应用条件。一正二定三相等2