一类指数超线性抛物方程的无穷时间爆破问题
罗森月,邓芳芳
(1 广东开放大学 广东理工职业学院 基础教学部, 广东 广州, 510091;2 广东开放大学 广东理工职业学院 信息与工程学院, 广东 广州, 510091)
1 概述和主要结果
本文中,笔者研究以下非局部抛物问题:


文献[1-2]研究了一类一般项的问题及其高维情形(带拉普拉斯算子)和有限时间爆破解的渐近性态. 特别地,对于式(1),若足够大,可得1);并且若足够小,可得2).关于半线性系统或具有此类反应项的退化方程的有限时间爆破的结果,可参考文献[3-4].在文献[5]中证明了,

则3)不可能发生.(2)的必要性在全局无界解中的作用尚不清楚.本文的目标是通过构造一类破坏条件(2)的广义函数解此问题,并且在该情形下的初始值使得3)可能发生.
本文的得到的定理如下:
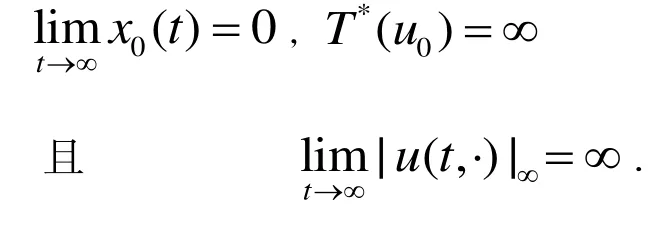
2 相关引理和定理1的证明
为研究方便起见,将(1)标记为

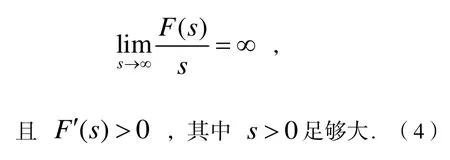
下面给出2个引理.


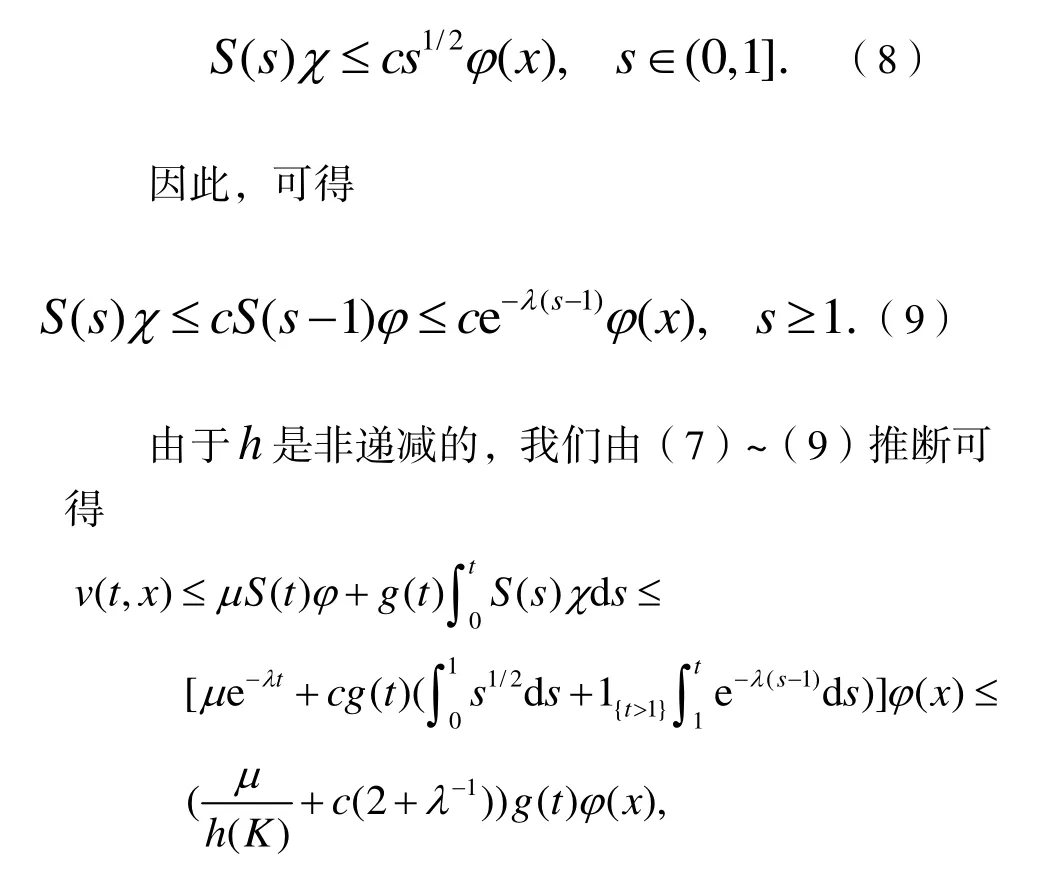
其中指标函数

由此得出上界的估计.
下面证明较低的估计.显然有

因此,较低的估计可得出.
经历了1 9 7 9年那个冬天,殷燕才知道真的战场远比《英雄儿女》里更糟糕。2月2 7日晨,东线最关键的谅山战役开始。有一个河南开封的兵李民,高个,白净,爱说爱笑,会拉手风琴,医院的女孩儿们都喜欢和他搭腔聊天,与殷燕相熟。“2月2 8日那天,从6 5 0高地上抬下来许多尸体。大家都在忙着工作,一个女兵突然惊呼:这不是李民吗!头的一半已被炮弹炸飞,军装被血浸透,担架里都是血水。要不是拿出他左上兜能够证明身份的生死牌,谁也不知道他就是李民。”殷燕回忆。
引理2设



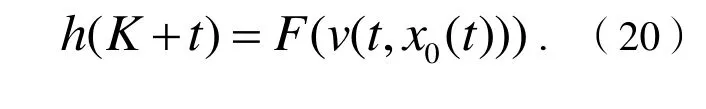
由引理1中的下界估计,

由引理1,有

从而得到(16).
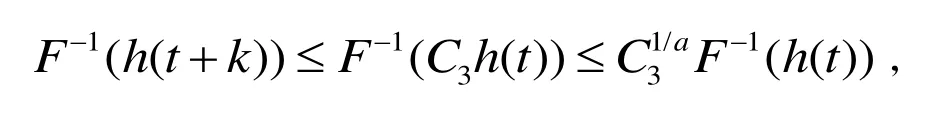
因此可得(17).

由引理2和注1可直接得出结论.
3 结论
本文中,笔者考虑了一类具有任意增长性的一般非线性抛物问题, 在合理的假设下, 得出了无穷时间爆破仍然发生的结论(见引理2或定理1).笔者采用间接的方法证明:首先求解一个线性热方程,其具有规定的空间常数,且右端函数在时增长到无穷大,并且对这个问题的解做了一些精确的估计.
对更一般的局部反应项的相关问题

在狄利克雷边界条件下,全局解的有界性问题一直是研究的热点课题. 特别地, 与 (1)不同的是,在空间维度 1 (或2)中(21)的无穷时间爆破从未发生(参考文献[9]), 但它可能在3或更高的维度中发生.在证明中得出了一类特殊的 1维的无穷时间爆破解的存在性. 这对进一步了解(21)的性质有一定助益.

