变系数G展开法与广义浅水波方程的精确解

王 鑫，岳晓蕊

(海南大学信息科学技术学院, 海南 海口 570228)

0 引言

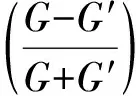
考虑由Boussinesq逼近法在经典浅水波理论中得到的广义浅水波方程[6-7]

uxxxt+αuxuxt+βutuxx-uxt-uxx=0

(1)

其中:α,β为任意非零常数且α+β≠0． 该方程一般用于描述浅水波在(1+1)维空间中的运动规律． 文献[7]证明了当参数α=β或α=2β时方程完全可积，并且通过反散射法验证了在此处的方程解的存在性；在文献[7]的基础上，文献[8]得到了方程的Hirota’s双线性形式； 通过运用Backlund变换的变量分离法，文献[9]求出了该方程变量分离并且含有低维任意函数的解； 文献[10]利用了新的G展开法得到了该方程的多种形式的行波解．

1 变系数G展开法

将非线性偏微分方程

P(u,ux;ut,uxx;uxt,utt; …)=0

(2)

作行波变换． 令u(x,t)=u(ξ)，ξ=x-ct，其中c表示波速，是一常数，则方程(2)化为

P(u,u′,u″, …)=0

(3)

设方程(2)的解为

(4)

这里的ai(ξ)(i=0, 1, 2, …,l)为待定的函数，参数l可通过齐次平衡法确定，G=G(ξ)满足一类二阶变系数非线性常微分方程

GG″+p(ξ)(G′)2+q(ξ)GG′=0

(5)

其中:p(ξ),q(ξ)均为ξ的任意函数． 借助Mathematica符号计算软件，可以得到方程(5)的解

其中:C1,C2为积分常数，同时可得：

(6)

2 广义浅水波方程的新精确解

设方程(1)有行波解u=u(ξ)=u(x-ct)，其中c是一非零常数，从而方程化为

cu(4)+c(α+β)u′u″+(1-c)u″=0

将上式关于ξ进行积分，并令积分常数为零，可得

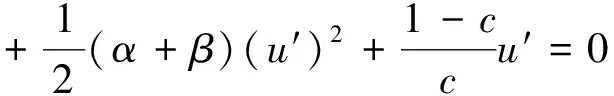
(7)

GG″+p(ξ)(G′)2+q(ξ)GG′=0

其中:p(ξ),q(ξ)为ξ的任意函数． 利用齐次平衡法，有2(l+1)=l+3，得l=1． 则方程(1)的解表示为

(8)

由方程(5)和式(8)可得

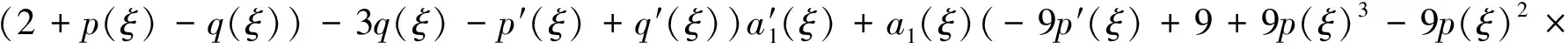
(q(ξ)-3)+q(ξ)(2(-1+q(ξ))q(ξ)-9+4p′(ξ))+5q′(ξ)+p(ξ)(27-2q(ξ)(9+q(ξ))-

3q′(ξ)+p′(ξ))+q′(ξ)+p(ξ)(-4q(ξ)2-9p′(ξ)+q′(ξ)+18)+2p″(ξ))-6(1+p(ξ))×

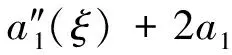
(q(ξ)-3+q(ξ)2+4p′(ξ))-2q′(ξ)-p(ξ)((q(ξ)-6)q(ξ)-9+6p′(ξ)+2q′(ξ))+

6(1+p(ξ) +q(ξ))a1″(ξ)+4a0‴(ξ))

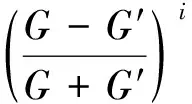
(9)

由式(9)～(11)，并借助Mathematica符号计算软件，可求得：

(14)

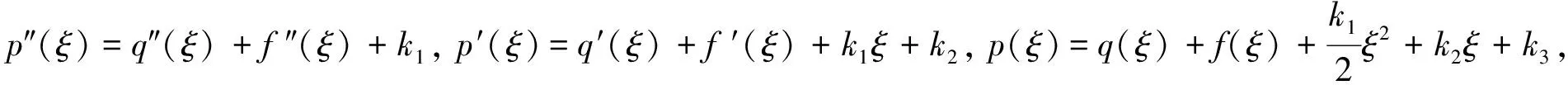
这里的C1>0，C2为任意常数． 将p(ξ)和q(ξ)代入式(6)，则有

其中:C3为任意常数． 再将p(ξ)和q(ξ)代入式(14)～ (15)，并进行积分求解可得：

(16)

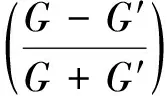
其中:C1<0.将p(ξ)和q(ξ)代入式(6)，则有

其中:C3为任意常数． 再将p(ξ)和q(ξ)代入式(14)～ (15)，并进行积分求解可得：

(19)

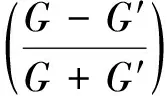
3 分析

文献[6]中的三角函数解是其中的一类情况，且较其含有更多的自由参数．

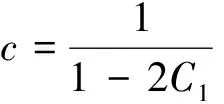
解中含有ξ的一次项，此类解是其他文献中没有出现过的新形式．

对于式(21)，其中C1≠0时，方程的解存在，且

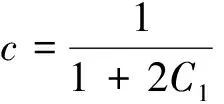
文献[6]中的双曲函数解是其中的一类情况，且含有更多的自由参数．

解中含有ξ的一次项，此类解是其他文献中没有出现过的新形式．

此变系数G展开法，主要是将G满足的方程改为了变系数方程，尝试用变系数方程作为辅助方程来求解常系数偏微分方程． 由于变系数的任意性从而扩大了函数G的范围，相应地，所求偏微分方程精确解的范围随之扩大，而且还囊括了辅助方程为相应的常系数方程的各类解的形式． 通过以广义浅水波方程为例进行求解，发现虽然辅助方程的系数扩展为函数，但中间的计算由于函数和其各阶导数的关系反而使得运算更加简单．

4 结语

本研究通过构造的一类变系数G展开法，对广义浅水波方程进行了研究，求得了该方程三角函数和双曲函数形式的显式行波解.由此可见，此类展开法不仅可以求得非线性偏微分方程的精确解，同时还可以得到方程解的多种形式.