三维空间瞬时声源的纯方位角估计性能分析

汪 海,崔逊学

(陆军炮兵防空兵学院,合肥 230000)

1 引 言

近年来目标定位技术越来越受到人们的重视,定位技术分为有源和无源两种[1].相对于雷达等有源定位而言,无源定位具有很强的隐蔽性和抗干扰性[2].到达时间差(Time Difference of Arrival,TDOA)作为无源定位的一种关键技术成为了一个新的研究方向[3,4].最近国内外研制出一些基于TDOA 技术的枪声定位系统,类似的声测系统在反恐安全、战场探测和其他领域具有重要应用背景[5].

无源定位包括无源测向和无源测距两类[6].当枪声、炮声和炸点等脉冲声波抵达传声器径向距离很远时,人们难以直接通过TDOA 双曲线交叉方法精确估计声源坐标[7,8].但如果在不同位置分散部署多个阵列,利用各阵列的TDOA 测量值可估计出瞬时声源的波达方向(Direction of Arrival,DOA)[9],这种技术方案也是本文研究的立足之点.

随着传感器、通信以及电子信息技术的发展,基于TDOA的声阵列定位算法得到了较充分的研究,到达时差方法常用于长基线声阵列对目标的定位.随着硬件设备性能的提升和数据采集器时间同步精度的提高,短基线声阵列采集的TDOA测量精度也越来越高.短基线时差测向相对于长基线来说,更具有应用优势,其优点在于维护方便,时间同步精度容易控制,接收的目标信号不易受气温和风向等影响[10].这些优点恰恰是战场应用所必需的.

为了满足低空目标和地面目标的被动声定位需求,提高战场瞬时声信号方位角的测向精度[11].本文对方位角/俯仰角联合估计加以改进,提出一种纯方位角估计方案,将三维空间阵列映射到平面上,利用平面阵列关系对三维空间瞬时声源的方位角进行估计.通过对其克拉姆-拉奥下界(Cramer-Rao Lower Bound,CRLB)进行分析,给出了纯方位角估计的可使用时机.仿真结果验证了纯方位角估计的可行性与有效性.

本文在现有硬件基础支撑下,从关键科学问题入手,最大限度地优化定位精度,所研究内容有望显著提高低空中远距离瞬时性脉冲声源的定位效果,为高精度被动声测定位系统的研制提供技术支撑.

2 联合估计及纯方位角估计

2.1 联合估计

图1为短基线传感器TDOA定向示意图,假设阵列由N个传感器构成,si为第i号传感器,坐标为(xi,yi,zi),接收到的时间为ti,各传感器之间的距离大约30m,高差大约为5m.取距离声源最近的传感器为基准传感器,即x0=y0=z0=0;M为瞬时声源的波达方向上的一点,M到基准传感器距离为2～3km,M在XOY平面上投影记为M′.

以基准传感器为坐标原点,令S=[x1,y1,z1;x2,y2,z2;…;xN-1,yN-1,zN-1],S为所有传感器和基准传感器之间的距离向量构成的矢量矩阵;时间差向量τ=[τ1,τ2,…,τN-1]T,其中τi=ti-t0;s0M与s0M′夹角为俯仰角θ,s0M′与X轴正向的夹角为方位角φ,令γ=[φ,θ]T.

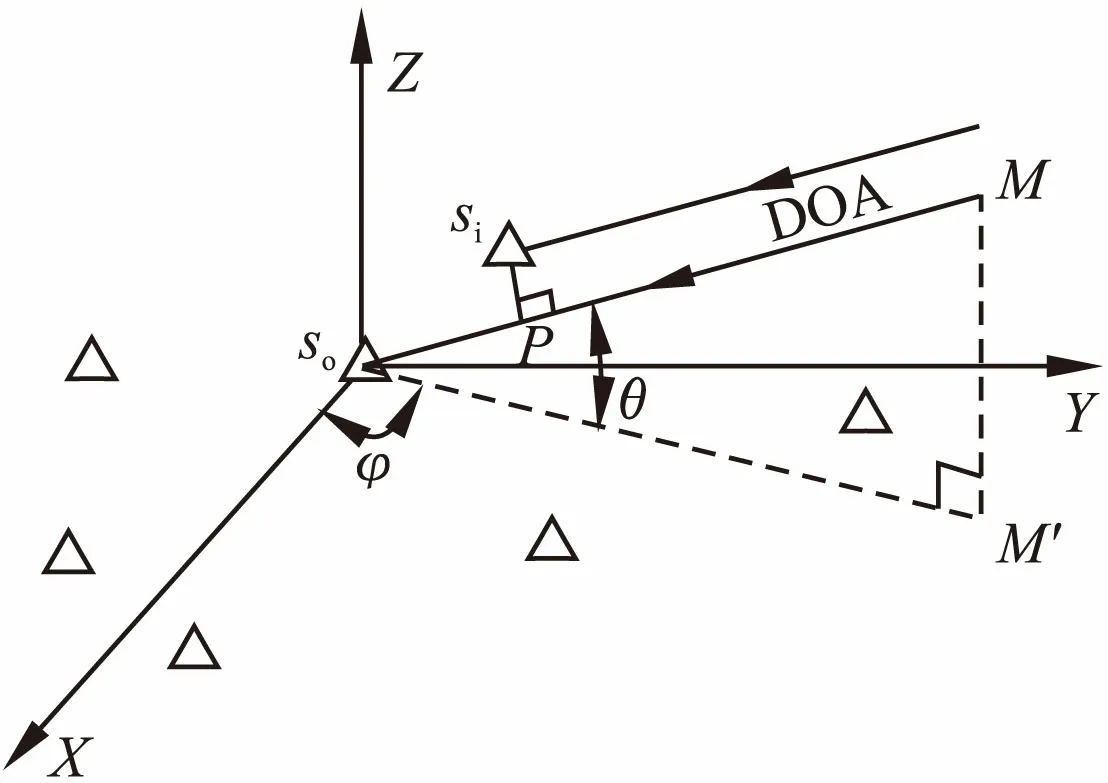
图1 基于TDOA的传感器阵列定向示意图Fig.1 Diagram illustrating TDOA-based direction finding with sensor array

由图1可知,s0P长度cτi等于si在s0M上的投影,即有下列TDOA方程:

cτi=sik

(1)

其中k为声源信号的单位方向向量

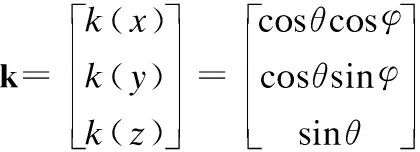
(2)

整理可得

cτi=xicosθcosφ+yicosθsinφ+zisinθ

(3)

2.2 纯方位角估计

针对平面波信号源和任意结构阵列的TDOA测向问题,本文提出一种纯方位角估计方案,根据TDOA测量值,将三维空间阵列映射为平面阵列,利用平面关系只对三维空间瞬时声源的方位角进行估计.图2为立体阵列与平面阵列到达时间的关系示意图,s0为基准传感器,si为第i个传感器(i=1,2,…,N-1),θ为基准传感器所估计的方位角,θi为第i个传感器所估计的方位角.设传感器M到s0传感器的时间为t0,到si传感器的时间为ti,则有:

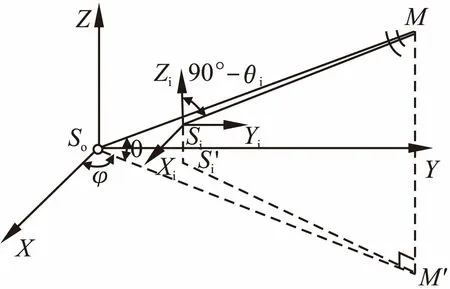
图2 立体阵列与平面阵列之间到达时间的关系Fig.2 Relationship of the arrival time between cubic array and planar array

τi=ti-t0

(4)

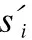
(5)

由于传感器阵列到声源距离远远大于传感器之间的距离,可以把θi≈θ,则:

(6)

将(3)式转化到平面上可得:

(7)

将(6)式代入(7)式可得纯方位角估计的测向模型:

cτicosθ=xicosφ+yisinφ

(8)

本文以近地面声源目标为研究对象,即θ通常小于10°,不妨令(8)式中cosθ≈1,则纯方位角估计的测向模型可简化为:

cτi=xicosφ+yisinφ

(9)

3 纯方位估计的理论分析

3.1 CRLB的比较

在参数估计领域中,CRLB是无偏估计的重要度量方法,是所有无偏估计算法的精度下界[12,13].针对文中两个模型的CRLB,这里提出以下命题.

命题1.纯方位角估计模型的CRLB小于联合估计模型的CRLB.

证明:如果存在噪声,则(1)式应改写为:

(10)

其中ni是相互独立测量噪声变量,其均值为0,方差为σni2,定义n=[n1,n2,…,nN-1]T

将(10)式整理成矩阵形式为:

(11)

如果误差是相互独立的高斯随机变量,则条件概率密度函数

(12)

令F(γ)为费歇尔信息矩阵(Fisher Information Matrix,FIM),其矩阵元素定义为:

(13)

则方向估计向量γ的费歇尔信息矩阵各元素如下:

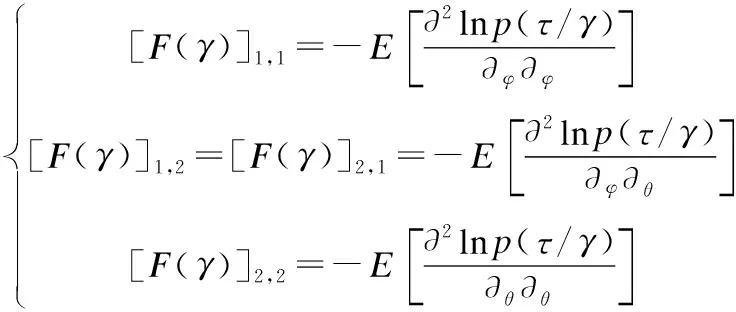
经过推导,可得到γ的费歇尔信息矩阵如下:

(14)

[F(γ)]1,2=[F(γ)]2,1

(15)

(16)

方向估计向量γ的第i个参数的克拉姆-拉奥下界定义为:

CRLB(γ)=[F-1(γ)]i,ii=1,2

(17)

根据克拉姆-拉奥下界定义可得方位角φ和俯仰角θ的CRLB为:

(18)

(19)

令Ai=xisinφ-yicosφ,Bi=xisinθcosφ+yisinθsinφ-zicosθ,则(18)式和(19)式可简化为:

(20)

(21)

纯方位角估计模型的CRLB与联合估计模型的CRLB推导原理类似,且比联合估计模型简单,在此直接给出推导结果：

(22)

(23)

(24)

很显然(23)式比(24)式小,即使用纯方位角估计方法测向精度更好.

根据CRLB推导结果,我们可以直接给出以下推论:

推论1.如果一个估计器的精度可以接近CRLB,那么,此估计器利用纯方位角估计进行测向,效果将更优.

3.2 高差对测向的影响

对于任意传感器阵列来说,推导传感器高差对测向精度影响的数学表达式是很困难的,不能得出相应的关系模型.本文将对一类特殊的传感器阵列进行理论分析.由于均匀分布的锥形传感器阵列,既有传感器高差,又有很高的测向精度,符合本文讨论需求,因此本文将对这一典型阵列进行理论分析.在本文第4节将用MATLAB仿真实验模拟任意传感器阵列的高差对测向精度的影响.

考虑高差对测向精度的影响,本文提出下述命题:

命题2.传感器间高差对方位角精度不产生影响,只影响俯仰角的精度,传感器间高差越大,俯仰角的精度越高.

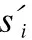
图3 均匀分布的锥形传感器阵列示意图Fig.3 Diagram of uniformly distributed cone array of sensors

由图3可得:

(25)

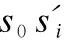
ai=cosφii+sinφij,i=1,2,…,N-1

(26)

由于各传感器均匀分布在圆周上,有

(27)

即

(28)

(29)

此时CRLB中的

Ui=xisinφ-yicosφ=ρcosφisinφ-ρsinφicosφ=ρsin(φ-φi)

(30)

Vi=xisinθcosφ+yisinθsinφ-zicosθ

=ρcosφisinθcosφ+ρsinφisinθsinφ-Hcosθ

=ρsinθcos(φi-φ)-Hcosθ

(31)

(32)

(33)

(34)

代入(20)式和(21)式可得:

(35)

(36)

从(35)式可以看出方位角的CRLB不受高差影响,从(36)式可以看出高差H越大,俯仰角的CRLB越小,即传感器间高差越大,俯仰角的精度越高.

4 仿真分析

仿真场景设置如下:设置8个传感器,假设传感器位置的X轴和Y轴坐标在30米半径的圆形内随机选取,Z轴坐标在较小的范围[-5,5]米内随机确定,这与通常的声探测野外部署条件是相似的;声源方向也是随机产生,方位角设置在[0°,90°]之间,俯仰角设置在[-5°,5°]之间;TDOA测量误差服从高斯分布,不考虑测量的系统偏差问题.本文仿真实验中,方位角/俯仰角联合估计简称为2-D,纯方位角估计简称为1-D.

4.1 仿真1

图4用仿真实验模拟了传感器间高差对俯仰角CRLB的影响,从图中可以看出,俯仰角的CRLB随着传感器间高差的增大而减小,当高差小时,俯仰角的CRLB很大,尤其在高差小于10m时,影响最为强烈,即短基线传感器阵列在估计低空目标方向时,得到的俯仰角精度受传感器高差影响很大.

图5模拟了传感器间高差对方位角CRLB的影响,从图中可以看出,高差对两个模型的方位角CRLB均不影响,本实验也验证了命题2的正确性.

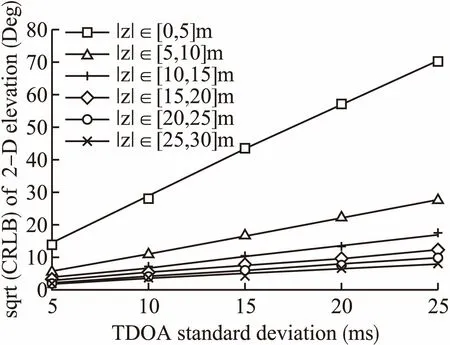
图4 高差对俯仰角CRLB的影响Fig.4 Height difference influence on CRLB of elevation

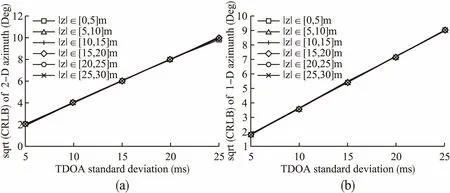
图5 高差对方位角CRLB的影响.(a)2-D.(b)1-DFig.5 Height difference influence on CRLB of azimuth.(a)2-D.(b)1-D

4.2 仿真2

图6绘制了1000次随机测试下定向结果累计分布函数(CDF)图像.用1-D TS表示使用纯方位角估计方法的泰勒展开算法;1-D LLS
表示使用纯方位角估计方法的最小二乘算法;2-D TS和2-D LLS表示联合估计模型的泰勒展开算法以及最小二乘算法.显然使用纯方位角估计方法能有效地提高测向精度.

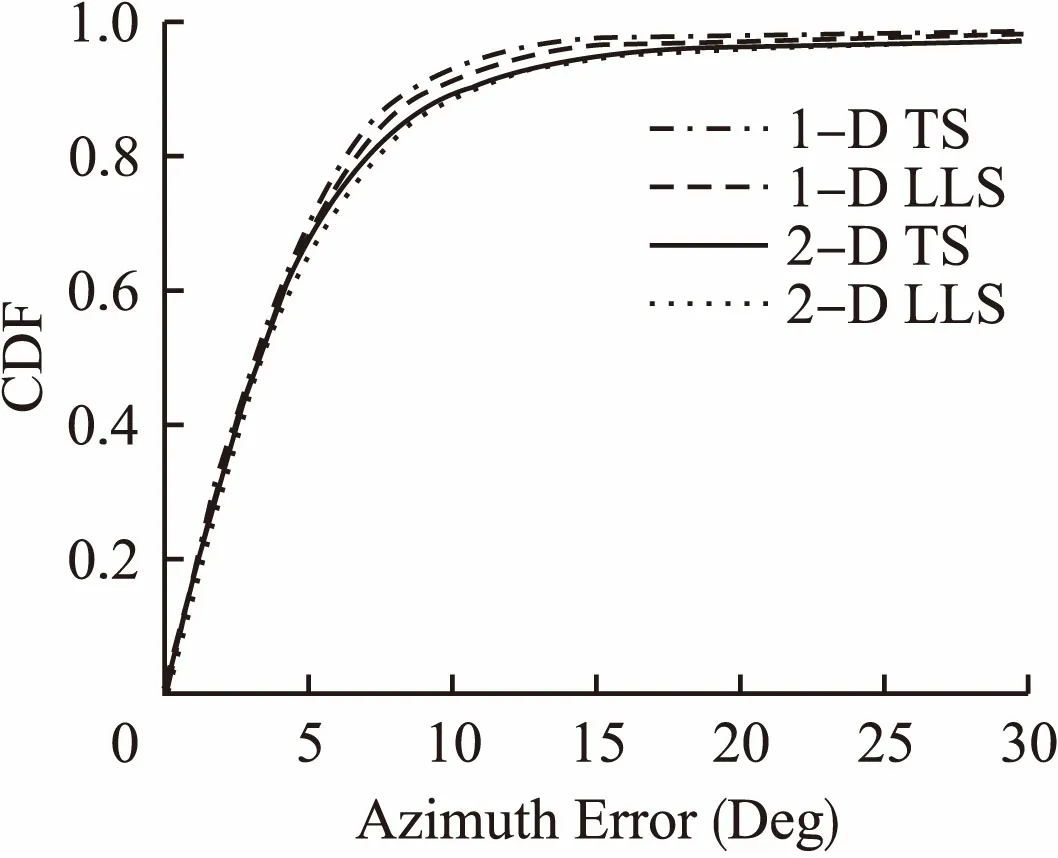
图6 测向结果累计分布函数曲线Fig.6 Cumulative distribution function curve of direction finding

4.3 仿真3

通过MATLAB实验对推论1加以验证,由附录A可知联合估计与纯方位角估计的泰勒展开算法的精度均可以接近CRLB,满足推论1中的条件.

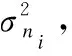
图7绘出了1-D TS与2-D TS两种泰勒展开算法、TS算法的CRLB、以及TS算法的协方差的RMSE定向误差随噪声误差变化关系.从图7可知,TS算法的协方差与CRLB重合为一条曲线,验证了泰勒展开算法的精度可以接近CRLB.随着信号噪声的增加,RMSE也随之增大,相比于2-D TS算法,1-D TS的定位误差更小,更接近CRLB下界,本实验也验证了推论1的正确性,即当一个估计器的精度可以接近CRLB时,将此估计器利用纯方位角估计进行测向,效果将更优.

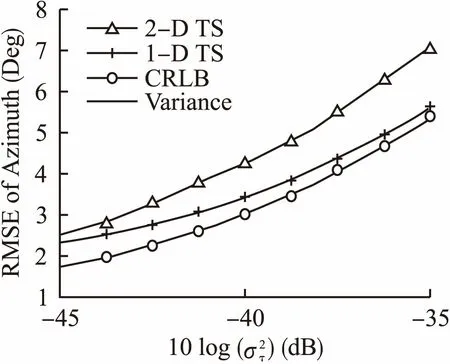
图7 泰勒展开算法的RMSE性能结果Fig.7 RMSE of Taylor expansion algorithm

5 结 论

针对平面波信号源和任意结构阵列的TDOA测向问题,本文推导了空间立体阵列根据TDOA测量值简化为平面阵列进行纯方位角估计的可行性.本文的推导过程是基于CRLB理论,并利用经典的测向方法进行了性能验证.理论分析和模拟实验表明,采用简化的平面阵列进行纯方位角估计的精度,要优于空间立体阵列对信号源进行方位角/俯仰角联合估计中的方位角精度.本文的研究结论特别适用于各种地形部署的传感器阵列对地面目标进行纯方位角估计的需求.

另外,本文研究还表明,阵列内部传感器之间的高度差只影响俯仰角估计精度,对方位角估计没有影响.因此,对于地面目标的纯方位角测向应用而言,在部署阵列时人们无需考虑有意增大传感器之间的高度差.