搏动式血泵的电磁驱动装置设计及可行性研究*

张磊，葛斌△，方旭晨，张少伟，魏凌轩，伍进平

(1.上海理工大学 医疗器械与食品学院，上海 200093；2.上海市杨浦区市东医院，上海 200438)

1 引 言

血泵作为一种动力源装置，被广泛应用在体外膜肺氧合(ECMO)、体外循环(CPB)、机械灌注(MP)[1-2]等领域。对于搏动泵而言，其优点在于可以降低血清中缩血管物质的浓度，抑制肾脏血管过度收缩[3-4]。同时，其驱动形式在很大程度上决定了整个系统的设计[5]，常见的驱动有电机驱动、气动、液压驱动等。由于气、液类驱动需外置气源装置，造成装置的便携性差，故较少使用。对于电机类驱动，实现搏动流输出的主要方式是借助机械转换机构，也因此降低了驱动装置的效率[6]。此外，由于全程输出刚性驱动力，在驱动血泵过程中容易使血液产生挤压，造成溶血，以及组织损伤。因此，为了达到理想的血泵搏动驱动，要求驱动装置能够[5,7]：具有满足每搏输出量需求的行程及外形大小；产生满足灌注压力需求的驱动力；产生与自然心率相近的往复运动频率。

因此，本研究基于电磁力学原理设计了一种新型搏动式血泵驱动装置，该装置能够输出往复直线运动，避免了复杂的机械转换。该装置在驱动过程中存在的“柔性驱动”能够避免因过载造成的血液破坏。此外，通过驱动电流的调节能够输出不同的灌注压力，满足实际的临床需求。

2 新型驱动装置结构

2.1 驱动装置结构

搏动泵主要由驱动装置和柱塞式泵头构成，其结构见图1。工作时柱塞左右滑动并配合单向阀实现血液的定向搏动输出。本研究的重点是驱动装置设计，故对泵头结构不予赘述。

图1 泵头剖视图Fig 1 Cutaway view of pump head

驱动装置结构见图2，包括驱动线圈和永磁动子，及其他辅助结构。其中，端盖和直线轴承均采用非磁性材料，推杆两端连接永磁动子与泵腔内柱塞。

图2 驱动装置整体剖视图Fig 2 Cutaway view of driving unit

2.2 新型驱动线圈结构设计

2.2.1电磁学原理 取永磁体边界上一段微元dx，并将该微元模型等效为的环形圆电流[8]，于是该微元圆电流在磁场中受到的安培力为[9]：

F圆=By2πRJmsdl=4(πR)2JmsBy

(1)

其中，Jms为面电流密度，Bx为轴向磁场分量，By为径向磁场分量，R为端面半径。

根据磁场中的高斯定理得：

(2)

将式(2)带入式(1)得：

(3)

则永磁体所受电磁力模型为：

2.2.2驱动线圈结构设计 基于上述模型提出新型结构驱动线圈见图3，该线圈由三个驱动绕组构成，各绕组结构见图3(a)、(b)、(c)。

图3 驱动线圈结构 (a).绕组3；(b).绕组1；(c).绕组2Fig 3 Cutaway view of driving coil (a). Winding 3; (b). Winding 1; (c). Winding 2

2.3 工作方案

设永磁动子的初始位置见图4(a)，且永磁体与通电线圈的极性方向相同，此时给绕组1、3通电，线圈内产生自右向左逐渐增强的磁场，并驱动永磁动子向左运动，当动子到达图4(b)所示位置时，控制绕组2、3通电，线圈内磁场的梯度方向改变，于是电磁力驱动动子重新运动到右端，如此交替供电可以实现动子往复运动，往复频率由单片机控制。

3 新型搏动驱动装置的解析模型

3.1 电磁驱动力模型

建立线圈驱动永磁体力学模型见图5。为了方便样机的制作以7层结构作为研究对象推导受力模型。将永磁铁等效成为厚度忽略不计的表面螺线管[10]，并通过互感计算电磁驱动力。

根据文献[10-12]可以通过线圈互感M计算得到线圈之间的相互作用力F，其中I1为永磁体等效电流，I2为驱动电流：

图4 驱动线圈原理示意图 (a).绕组1、3通电；(b).绕组2、3通电Fig 4 Working principle diagram of driving coil (a). Drive winding 1 and 3 to work； (b). Drive winding 2 and 3 to work

图5 磁力模型原理图Fig 5 Schematic diagram of magnetic force model

(4)

分别对单段螺线管进行分析，并将所得到的结果进行累加，于是得到沿着z轴的互感为：

(5)

其中，r0=(z1-z2)2+R2+r2-2Rrcosθ，i为螺线管层数，μ0为真空磁导率，N1为永磁体等效线圈匝数，N2为驱动线圈匝数，Z1为线圈长度，Z2为端面距离，H为磁体厚度，R为磁体半径，R1为线圈内径，R2为线圈外径，d为线径。根据文献[13-14]可知，永磁体等效成螺线管满足：

(6)

其中，Br为永磁体剩磁，结合式(4)、(5)、(6)可以得到电磁轴驱动力模型：

(7)

3.2 新型驱动线圈结构参数

由式(7)可以看出驱动力与线圈的直径、长度、导线直径以及磁体厚度相关。本研究通过设计正交试验选出最优参数组合。利用SPSS将各因素水平的顺序进行随机处理见表1，选用正交试验表L16(45) 进行正交实验，驱动电流设置为1 A。

表1 因素水平表

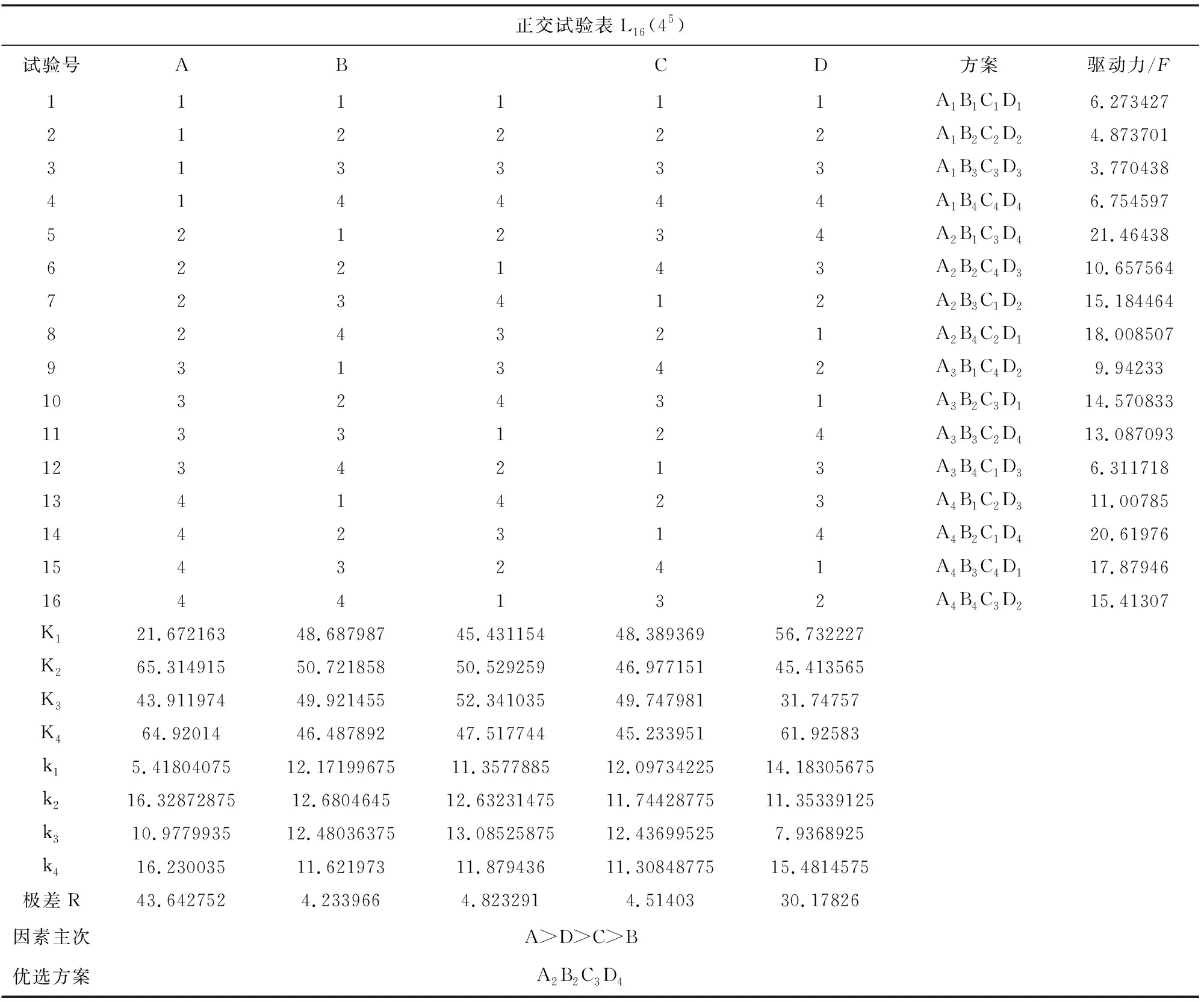
通过对比分析表2中数据可知，线圈内径对磁力影响最大，其次是磁体厚度、导线直径、线圈长度。比较试验指标选用最优组合为线圈内径0.025 m、线圈长度0.09 m、导线直径0.0005 m、磁体厚度0.05 m。

3.3 装置驱动效率分析

该装置将电能转换为动子的动能，以推动血液实现搏动输出。其转换效率可以计算为电能与动子输出的动能之比：

(8)

其中，I—驱动电流，U—驱动电压，F—动子推力，v—动子运动速度。

4 实验

按照正交实验结果设计实验样机结构见图6，主要参数有：装置总长为250 mm，主体长150 mm，内径为50 mm，外径54 mm，壳体材料为PMMA;线圈长度为90 mm，线径为0.5 mm漆包线;柱形永磁动子直径为50 mm，高度为50 mm，材料为N35H型钕铁硼，质量为0.442 Kg;直线轴承和推杆均采用非磁性304不锈钢，推杆直径为5 mm。

图6 驱动装置图Fig 6 Drive device size diagram 表2 正交试验方案 Table 2 Orthogonal test table

正交试验表L16(45)试验号ABCD方案驱动力/F111111A1B1C1D16.273427212222A1B2C2D24.873701313333A1B3C3D33.770438414444A1B4C4D46.754597521234A2B1C3D421.46438622143A2B2C4D310.657564723412A2B3C1D215.184464824321A2B4C2D118.008507931342A3B1C4D29.942331032431A3B2C3D114.5708331133124A3B3C2D413.0870931234213A3B4C1D36.3117181341423A4B1C2D311.007851442314A4B2C1D420.619761543241A4B3C4D117.879461644132A4B4C3D215.41307K121.67216348.68798745.43115448.38936956.732227K265.31491550.72185850.52925946.97715145.413565K343.91197449.92145552.34103549.74798131.74757K464.9201446.48789247.51774445.23395161.92583k15.4180407512.1719967511.357788512.0973422514.18305675k216.3287287512.680464512.6323147511.7442877511.35339125k310.977993512.4803637513.0852587512.436995257.9368925k416.23003511.62197311.87943611.3084877515.4814575极差R43.6427524.2339664.8232914.5140330.17826因素主次A>D>C>B优选方案A2B2C3D4

4.1 驱动装置测试

为了测试对比理论值与实验值，设计图7所示静力测试系统，其中直流电源型号为GPS-4303C，弹簧测力计型号NK-30。实验选用1.5 A驱动电流，在线圈轴向均布10个位置点，并对每个位置点进行20次拉力测量，最后将测得的实验值与理论值绘制成图8。

图8驱动力曲线图

Fig8Staticcurvediagramofpermanentmagnet

从图8中可以看出实验曲线和理论曲线表现出相同的规律，且当驱动力为正时，理论值偏大，而驱动力为负时，理论值偏小。这主要是由于摩擦力与驱动力反向和同向导致的。其中“0～5”为“刚性驱动”阶段，该阶段驱动力平稳在10～14 N之间，保证了血泵的正常工作；5点之后受力逐渐减小，7点为受力平衡点，这一阶段为“柔性驱动”阶段，该阶段设计避免了因过载造成的血液破坏，保护了血细胞及灌注组织；当动子越过平衡位置7时，反向驱动力逐渐增大，这使得动子在短时间内实现减速直至停止，避免了因机械惯性造成的撞击和振动，使装置保持平稳运行。

4.2 模拟体外实验研究

为了进一步研究该装置在驱动泵头工作时的流量和压力性能，进行了模拟体外循环实验。见图9，驱动装置与泵头连接，构成搏动泵系统，并将该系统连接到模拟体外循环管路中，测量平均灌注压和每搏输出量。泵腔内柱塞直径30 mm，厚度20 mm，泵腔长度为70 mm。系统中的循环介质为动物灌注液，其粘度与血液类似。

图9搏动泵实物图

Fig9Pulsatingpumpsystemphysicaldiagram

4.2.1灌注压力与电流的关系研究 基于模拟体

外循环实验平台，对该装置平均灌注压输出特性作出研究。实验采用的压力传感器型号为YW-131，结果见图10。结果显示平均灌注压与驱动电流呈正相关，其拟合方程为y=33.074x+6.6563，R2=0.9784。由于该装置的输出压力只与驱动力相关，因此该拟合方程在满足驱动时的所有电流下均适用，在临床中能够根据目标灌注压调节驱动电流以满足临床要求。

图10 驱动电流与压力关系图Fig 10 Diagram of relation between driving current and pressure

4.2.2每搏输出量研究 每搏输出量由泵腔的工作容积以及输出压力决定。参考压力实验，设置输出压力分别为40、50、60、70、80 mmHg，驱动电流分别为1.1、1.4、1.7、2、2.3、2.6 A，研究驱动电流、流量和压力的关系，实验采用称重的方式测流量，已知泵头容积为49.5 mL，结果表3。

表3 每搏输出量与容积效率

从表3中可以看出每搏输出量与驱动电流呈正比，与输出压力呈反比。不同的输出压力对应完全灌注(容积效率达到90%以上)时的驱动电流也不同，这是由螺线管驱动力特性决定的。驱动电流、流量和压力三者的变化规律见表3，在临床中可以参考表3选出相应的电流，以获得相应的流量满足临床需求。

4.2.3搏动灌注压测试及效率分析 基于实验台对装置搏动特性及加速度特性进行研究，实验以人在安静状态下的平均动脉压100 mmHg为灌注目标[15]，按照灌注压拟合方程计算得到驱动电流为2.82 A。由于设备原因实际选用的驱动电流为2.8 A，驱动电压为31.3 V，搏动频率周期为0.8 s，管路负荷为80 mmHg。

压力波形见图11，压力范围为80～120 mmHg，平均灌注压为100 mmHg且搏动特性明显。由于循环管路的弹性作用，使压力波形在下降至接近最低压时出现减缓。这说明本研究设计的驱动装置能按照设定的压力值输出，且能够很好地满足临床需求。

图12为动子的加速度波形，图中横轴表示时间(单位格表示40 ms)，纵轴表示电压 (单位格表示100 mV)，从波形中可以看出，动子的加速时间即做功时间大约为60 ms，故动子的平均速度为0.67 m/s。根据式(7)计算得出在驱动电流为2.8 A时动子的平均电磁力为28.7 N，再结合式(8)计算可得，该驱动装置的驱动效率近似为21.83%。

图11 压力波形图Fig 11 Pulsating pressure waveform diagram

图12 动子加速度波形Fig 12 The waveform of acceleration of permanent magnet

5 结论

本研究基于电磁学原理设计出一种新型搏动式血泵驱动装置，该装置能够输出搏动流。所运用的堆叠螺线管驱动线圈结构系首次提出，通过实验和理论分析得出，该结构驱动线圈在设计过程中所依据的理论基础及数学模型是正确的，且设计过程科学合理。该结构在满足驱动的同时能够避免因系统过载对血液造成的机械压迫。此外，该驱动装置能够根据设定的压力值选择驱动电流特性很好地满足了在实际临床中的需要。

通过理论分析与实验研究，验证了该装置作为搏动式血泵驱动的可行性，但就其作为一整套驱动系统而言尚缺乏对实时数据的采集与反馈，且该驱动装置的驱动效率仍有待改进，在后续的研究中会逐一进行完善。