考虑连杆惯性参数的三缸发动机激励建模与分析

左曙光，王 珺，周大为，阎 礁，安一领，吴旭东

(1. 同济大学 汽车学院，上海 201804； 2. 泛亚汽车技术中心有限公司，上海 201201)

往复式内燃机是现代汽车的主要动力源，为汽车提供动力的同时也是一个主要的振动激励源。为了满足国家排放法规的限制以及节能减排的目标，目前越来越多的汽车上使用了小型化的三缸发动机。三缸发动机无法抵消曲柄连杆机构运动产生的不平衡惯性力矩，存在怠速抖动等振动问题，其NVH(Noise Vibration and Harshness)检查性能较差[1]。在动力总成悬置系统的设计、优化过程中，准确计算振动激励是进行系统设计的重要前提。随着人们对于乘坐舒适性的重视，对悬置系统的设计提出了更高要求，需要准确地对发动机振动激励进行建模解析。目前关于发动机动力学建模和激励计算的研究大多针对偶数缸发动机，而三缸发动机的激励阶次成分复杂，这些方法无法准确反映三缸发动机实际运行状态下的振动激励特性，因此考虑需要对三缸发动机曲柄连杆机构进行动力学建模，求解其振动激励。

发动机的振动激励主要包含两种成分：气缸内气体燃烧压力而引起的绕曲轴轴线方向并向外传递的负载力矩以及活塞、连杆等零部件运动产生的惯性力、惯性力矩。对于三缸发动机而言，曲轴负载力矩为1.5阶及其倍数，而惯性力及惯性力矩为1阶及其倍数，二者振动能量相当，均需要准确建模计算。

目前，发动机振动激励的理论计算中大多使用一种简化的方法[2-5]，先研究单缸发动机的曲柄连杆机构，将连杆等效成位于活塞销及曲柄销处的两个质量块，与曲轴、活塞一起构成双质量系统，根据运动学关系推导单缸发动机的激励，然后根据多缸发动机各缸相位差推广到多缸发动机，得到多缸发动机的振动激励，这种方法进行了大量简化，没有充分考虑曲柄连杆机构部件的惯性参数，尤其是连杆，也没有考虑各气缸之间的气体压力、相位差等参数的差异，导致对于三缸发动机的激励计算精度不足。密歇根大学的Hoffman等[6]基于多体动力学中的凯恩方法进行了发动机振动激励的理论计算，建立了发动机缸体与曲柄连杆机构相互耦合的7自由度模型进而计算振动激励，算法过于复杂，实际工程中不需要考虑发动机缸体对于曲柄连杆机构运动的影响，采用单向耦合的模型即可达到较高精度。伊朗的Fakhari等[7]基于拉格朗日法及牛顿欧拉方程详细推导了曲柄连杆机构中活塞侧向力、主轴承受力等，但对于动力总成来说，这些都是系统内力，不应计入振动激励。何智成等[8]通过实验对动力总成悬置系统的激励进行了识别，建立了等效激励参数模型，利用遗传算法，以仿真与实验结果的差异为目标函数，对加速度曲线进行拟合，识别出了等效激励参数。刘晓昂[9]采用悬置变形法，在动力总成振动特性实验的基础上，结合动力总成刚体模型，识别了等效激励。总的来说，现有激励计算或识别方法存在精度不高、过于复杂等不足，并且大多针对偶数缸发动机，对于三缸发动机振动激励的建模计算研究较少。

本文采用了一种基于多体动力学中拉格朗日乘子法的曲柄连杆机构建模方法，推导了三缸发动机振动激励的理论表达式。以某三缸发动机动力总成系统为例，计算了其振动激励，在考虑液压悬置频变特性的动力总成位移模型中仿真了各个悬置点的振动加速度响应，与实车测量结果以及通过简化方法计算激励进行仿真得到的结果进行了对比验证。

1 基于多体动力学的发动机激励计算

1.1 计算假设及坐标系规定

(1)计算假设

在悬置系统开发阶段发动机往往设计锁定，发动机各气缸内气体压力以及曲轴转角随时间变化的关系可根据实验或有限元仿真得到，因此认为这两个参数的变化规律已知并将其作为计算激励的输入。

由于发动机缸体的振动相对于曲柄连杆机构的运动而言较小，模型中忽略了其对于曲柄连杆机构运动特性的影响，计算激励时假设发动机缸体处于静止状态，仅考虑曲柄连杆机构的运动，计算出激励后再附加到缸体上计算振动响应，属于单向耦合。

假设动机内部润滑良好，计算中不考虑主轴承、活塞等处的摩擦损失，也不考虑重力势能的影响。

(2)坐标系规定

计算激励时使用的发动机坐标系(Engine Coordinate System, ECS)如图1所示，坐标系原点O位于远离飞轮的第一缸轴线与曲轴轴线交点处，x轴沿曲轴轴线方向指向飞轮、变速器一侧，z轴沿第一缸轴线方向指向上方，y轴根据右手定则确定。

图1 发动机坐标系示意图Fig.1 Schematic diagram of engine coordinate system

1.2 曲轴负载力矩计算

将曲柄连杆机构从发动机中分离出来，包括曲轴、连杆、活塞、飞轮、皮带轮等。本质上，这是一个单自由度系统，但为简化推导过程，选取第i缸活塞z向位移zpi、第i缸连杆转角βi及曲轴转角α共7个广义坐标(i=1,2,3)，如图2所示，图中Cpi表示第i缸活塞质心位置，近似看作位于活塞销中心处；Ccri表示第i缸连杆质心位置，用ycri及zcri表示其位置；文中i均表示第i缸，i=1,2,3。

图2 曲柄连杆机构示意图Fig.2 Schematic diagram of crank mechanism

由于自动度数小于广义坐标数，需使用带乘子的拉格朗日方程[10]

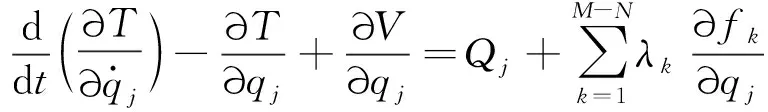
(1)

式中:qj为第j个广义坐标；T为系统动能；V为系统势能；Qj为第j个广义坐标上的作用力；M为广义坐标数目；N为自由度数；λk为第k个拉格朗日乘子；fk为第k个约束方程；k为约束方程编号。

根据各个气缸的几何约束关系，引入6个约束方程

(2)

式中:f1i为第i缸的第1个约束方程；f2i为第i缸的第2个约束方程；r为曲柄半径；lcr为连杆长度；φi为第i缸与第1缸的曲柄转角相位差。

系统动能分为三部分：曲轴的转动动能、活塞直线运动动能以及连杆平面运动动能，可以表示为

(3)

式中:Ics为包含飞轮、皮带轮的曲轴转动惯量；mp为活塞质量；mcr为连杆质量；Icr为连杆绕其质心的转动惯量；l为连杆质心到连杆小头的距离；vcri为第i缸连杆的质心速度，可表示为

(4)

式中:n1，n2分别为沿y，z轴的单位向量。

由于不考虑重力影响，系统势能不变，即

V=const

(5)

曲柄连杆机构在各个广义坐标上受到的外力为

(6)

式中:Tload为曲轴受到的负载力矩；Fgi为第i缸活塞受到的气体力；pgi为第i缸内的气体相对压力；D为活塞直径。

将式(2)～式(6)代入式(1)中，得到系统的振动微分方程组，包含7个方程

(7)

式中:λ1i为第i缸的第1个拉格朗日乘子；λ2i为第i缸的第2个拉格朗日乘子。

为简化计算结果，引入一些变量

《说文》中说：“把，握也。从手，巴声。”可见“把”的本义为“握”“持”，即将物拿在手里，为动词。后来由“握持”义引申为“把持”“控制”“掌管”义。此时“把”的结构形式为把+NP

(8)

将式(8)代入式(7)并求解方程组，消去拉格朗日乘子，得到曲轴负载力矩表达式为

(9)

式中:I1，I2为曲轴转角的函数，其表达式为

(10)

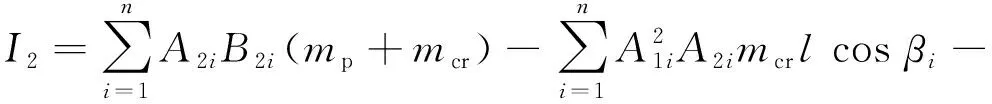
(11)

1.3 惯性力及惯性力矩计算

惯性力及惯性力矩包含两部分，往复运动部件产生的惯性力及旋转部件产的惯性力矩。

(1)往复惯性力

由于曲轴往往经过动平衡，其质心位于旋转轴线上，不会产生往复惯性力，因此，仅考虑活塞以及连杆的往复惯性力。

对于第i缸活塞，仅存在z向惯性力

(12)

对于第i缸连杆，同时存在y向以及z向的惯性力

(13)

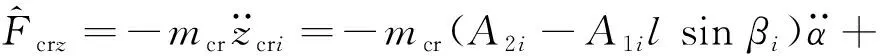
(14)

(2)旋转惯性力矩

旋转部件为曲轴和连杆，产生绕x轴的惯性力矩。

对于曲轴

(15)

对于第i缸连杆

(16)

(3)合力及合力矩

将各缸惯性力及惯性力矩平移至坐标系原点，得到总的惯性力及惯性力矩

(17)

(18)

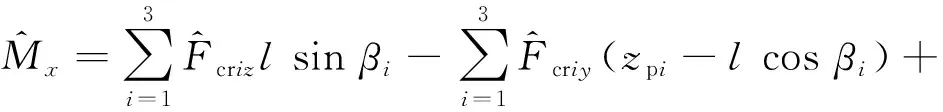
(19)

(20)

(21)

式中:si为第i缸轴线到原点的距离。

1.4 激励计算结果

将负载力矩与惯性力(矩)按发动机坐标系中的x，y，z平动及转动方向合成，得到总的激励，共6个分量

(22)

2 激励力分析及实验验证

为验证发动机激励计算的准确性，通常采用的方法有两种：一是直接法，采用传递路径分析等方法反推激励；二是间接法，通过对比动力总成悬置点振动响应实测值与仿真值来验证激励计算的准确性。直接法复杂繁琐，而间接法简单直接，精度能满足工程需求，故选择间接法。实验及仿真对象是带有变速器的动力总成，在怠速条件下，激励只来源于发动机，变速器的影响较小，其负载已包含在发动机曲轴负载中。

某三缸发动机、双离合变速器组成的动力总成系统，采用三点悬置，发动机悬置为液压悬置，变速器悬置为橡胶悬置，第三点为防扭拉杆。以该系统为例，计算分析了振动激励，用于动力总成悬置系统的振动特性仿真计算，与实验测试结果进行了对比。

2.1 三缸发动机振动激励分析

根据前文的计算方法，编写MATLAB计算程序计算曲轴负载力矩以及惯性力，图3列出了主要的计算结果。可以发现，由于考虑了连杆的惯性参数，三缸发动机不仅包含绕y轴的惯性力矩，还包含绕z轴的惯性力矩，二者处于同样的数量级，而由文献中的简化方法计算出的激励往往不包含绕z轴的不平衡惯性力矩。由于绕x轴的不平衡惯性力矩与负载力矩相比很小，这里不再分析。此外，对于不平衡惯性力，两种算法的计算结果都很接近0，可以忽略。

(a) 曲轴负载力矩 (b) 绕y轴的惯性力矩 (c) 绕z轴的惯性力矩图3 主要激励计算结果Fig.3 Calculation result of typical excitations

2.2 动力总成悬置系统振动仿真

怠速状态下，动力总成系统的振动激励只来源于发动机，此时计算出的激励可以用于动力总成悬置系统的振动仿真。仿真计算时把变速器当作一个刚体附加到了发动机缸体上，共同计算惯性参数后再用于仿真，这是很多文献中的常见做法，变速器的结构形式和零部件参数对于仿真结果的影响很小，带上变速器后，气缸压力及转速增加，带来的负载已包含在曲轴的负载Tload中。

由于本例中悬置安装方向与整车坐标系(Vehicle Coordinate System, VCS)相同，为方便动力总成悬置系统的建模、描述悬置点的振动情况以及与整车振动评价指标进行比对，建模时采用整车坐标系，原点位于动力总成质心位置，x轴向后，y轴向上，z轴向上。需将根据ECS计算出的激励转换为VCS中的激励再施加，得到的仿真结果也是基于VCS方向。

本文采用的动力总成位移计算模型为6自由度刚体模型，如图4所示，悬置简化为无质量的线性三向弹簧阻尼元件，不考虑车身及悬架的影响。该模型应用十分广泛，根据参考文献[11]可推导其振动微分方程，这里不再赘述。

本例中第三点悬置为防扭拉杆，可将其视为一个位于防扭拉杆与动力总成连接处的橡胶悬置，采用其衬套的刚度及阻尼[12]。

对于系统中的液压悬置，其动刚度具有强烈的频变及幅变特性，为仿真其频变特性，可以近似将液压悬置看作一个橡胶悬置附加了液压系统，橡胶悬置的刚度、阻尼由液压悬置的橡胶主簧决定，液压系统将产生一个随液压悬置变形量及其频率变化的液压力附加在振动激励中[13]。

考虑了液压悬置后的仿真系统框图如图5所示，在MATLAB/Simulink中搭建相应模型，分别代入本文算法以及根据参考文献[1-5]中的简化方法算出的振动激励，仿真了动力总成悬置系统的振动响应，得到各个悬置点主动端的振动加速度。

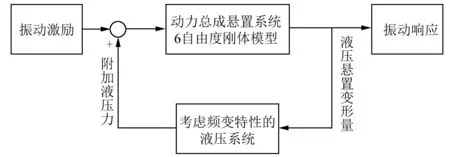
图5 考虑液压悬置后的仿真系统框图Fig.5 Block diagram of simulation program considering hydraulic engine mount

2.3 动力总成悬置系统振动实验

算例中车型存在怠速抖动问题，对其怠速振动特性进行了实车实验测量。

实验采用的数采是德国ZODIAC AEROSPACE公司生产的，型号为DIC24 plus，如图6所示，采样频率设为32 000 Hz。实验中将3个三向加速度传感器分别布置在发动机悬置、变速器悬置、防扭拉杆主动端，如图7所示。

图6 数据采集仪Fig.6 Data acquisition instrument

(a) 发动机悬置主动端 (b) 变速器悬置主动端

(c) 防扭拉杆主动端图7 加速度传感器布置图Fig.7 Accelerometers’ layout

实验中，将变速器置于D挡，此时怠速抖动情况最为剧烈，记录各个悬置上支点即主动端的振动加速度。

图8列出了发动机悬置及变速器悬置点主动端的振动加速度频谱，防扭拉杆处仿真中过于简化，数据参考价值不大，不再考虑。从图中可以看出，不论使用何种方法，峰值频率都可以对应。此外，在0～5 Hz内，实测值在有些方向上出现了峰值，是由传感器测量到的背景噪声引起的，与系统特性无关。

(a) 发动机悬置主动端x向振动加速度 (b) 发动机悬置主动端y向振动加速度 (c) 发动机悬置主动端z向振动加速度

(d) 变速器悬置主动端x向振动加速度 (e) 变速器悬置主动端y向振动加速度 (f) 变速器悬置主动端z向振动加速度图8 悬置主动端振动加速度频域曲线Fig.8 Acceleration results at mount locations of different methods and experiment in frequency domain

D挡怠速时转速为950 r/min，频率为15.83 Hz，三缸发动机的主要振动激励及响应为1阶及1.5阶，这两阶频率下的振动加速度相对误差见表1。

由表1可以看出，在1.5阶，两种算法的准确程度相当，这是由于1.5阶激励主要为气体燃烧引起的，受到惯性参数的影响很小，两种算法都是由气体压力直接计算激励，在稳态情况下二者的计算结果很接近。而在1阶，考虑了曲柄连杆机构惯性参数后进行仿真得到的结果相比于简化方法在大多数方向上与实验结果更加吻合。此外，各个悬置点的z向振动都存在不够准确的情况，这是由于仿真时仅考虑了液压悬置的频变特性，没有考虑其幅变因素的影响，导致仿真结果出现偏差。在高频段，两种方法的计算结果接近，峰值频率可以对应，但幅值均出现了较大误差，很可能是液压悬置的高频硬化现象引起的，而与激励计算的准确性无关，从工程应用角度来说，低频段对于振动加速度均方根值的贡献更大，高频段的误差是可以接受的，若要减小这种误差，需要考虑液压悬置硬化现象对仿真进行修正。

表1 主要阶次的振动加速度相对误差Tab.1 Relative error of accelerationon the main order %

3 结 论

本文采用了一种新的三缸发动机振动激励建模计算方法，考虑了曲柄连杆机构中连杆等各部件的惯性参数，基于拉格朗日乘子法推导了振动激励的理论表达式。

以怠速工况下包含某三缸发动机的动力总成系统为例，使用本文方法以及文献中的简化方法分别计算了振动激励，发现相比于简化方法，考虑了连杆的惯性参数后，多出了绕z轴的不平衡惯性力矩，与绕y轴的惯性力矩数量级相当。绕x轴的惯性力矩与负载力矩相比很小，可以忽略。此外，两种算法算出的不平衡惯性力合力都近似为0，也可忽略。

将激励施加到动力总成悬置系统模型中，仿真了各悬置点的振动加速度响应，在怠速工况对该样车悬置点的振动加速度进行了测量，将仿真结果与实测结果进行了对比，结果表明，考虑连杆等部件的惯性参数后计算出的激励相比于简化方法具有更好的准确性，主要体现在各悬置点x,y方向的1阶振动加速度上，这主要由于考虑了连杆惯性参数后绕z轴的不平衡惯性力矩未被忽略。

本文的建模计算方法可以推广到含有任意结构形式的发动机，并且可以用于非稳态工况，如加速过程的仿真，算法中允许各个气缸的参数存在差异，如各缸气体压力差异、点火提前角引起的相位差波动等，更适合应用于要求较高计算准确性的场合，如动力总成悬置系统的优化设计、主动悬置的设计及其控制策略的研究、传动系统的扭转减振等。