基于叠加法消除CMUT测量拖尾的研究

郑冠儒，张 慧，李 志，曾周末

(天津大学 精密测试技术与仪器国家重点实验室,天津 300072)

空气耦合式超声检测作为一种非接触式的检测技术有着广泛的应用前景，包括木材[1]、电子封装材料[2]、以及复合材料的缺陷检测。最新的研究成果将此项技术应用于人机交互[3]和医学成像[4]等前沿领域。在这些研究当中，空气耦合的超声传感器是最核心的部分。目前，针对空气耦合式超声传感器的众多研究中，利用硅材料加工的硅微声学器件是其中的热门方向。硅结构微加工超声传感器可分为两类，分别是电容式微加工超声换能器(Capacitive Micromachined Ultrasonic Transducer，CMUT)和压电式微加工超声换能器(Piezoelectric Micromachined Ultrasonic Transducer，PMUT)。CMUT的结构主要可以分为以下几部分，分别是顶层电极、振动薄膜、空腔、绝缘层和基底。相对于PMUT来说，CMUT的振动膜结构使得其机电耦合效率更高，并且在接收灵敏度、带宽范围等各项指标上均优于PMUT。虽然CMUT本身相较于传统换能器的性能更佳，但是在空气的应用场景当中，依然存在着较大的声阻抗不匹配的问题，这一问题很大程度上体现在拖尾信号的产生当中。

对于CMUT传感器，在激励信号结束后，传感器的振膜将在电气阻尼和机械阻尼的作用下，产生自由阻尼振动。由于空气的密度较低，系统的阻尼系数很小，因此系统的调节时间会变的很长。这会使得CMUT传感器在激励结束进入接收状态之后，系统将会输出一段很长的拖尾信号，在此期间接收到的回波信号将会被拖尾信号所湮没，难以提取出来。由于拖尾信号的覆盖而导致回波信号无法被识别的区域称为测量盲区。对于近距离障碍物的测距，由于目标和传感器距离很近，盲区过大将会导致传感器的测距性能变差甚至无法提取到障碍物的距离信息，从而影响其适用范围。拖尾信号的持续时间和激励信号的能量有关，能量越大，换能器所激发出的拖尾信号持续时间也就越久。实验表明，对于圆形的CMUT振膜，在小功率激励信号下，拖尾的长度会在200 μs以上，对应的盲区范围在6.8 cm以上，小于此距离的目标障碍物的回波信号将无法被提取到。

消除拖尾信号的办法一般有三种，第一种是根据被测量障碍物到传感器距离的远近而改变发射信号的发射功率，对于较近的障碍物发射小功率信号来减小拖尾信号[5]；第二种是在信号提取环节，设计拖尾消除电路[6]，将传感器看作是电容电阻模型，通过添加负载来起到将能量快速衰减的作用；第三种是利用叠加法[7]，在传感器激励信号结束之后再激发出一个和原信号相位相差半个周期的反相信号，利用叠加原理来消除多余的拖尾部分。针对CMUT器件，为获得较高的灵敏度往往需要加载较大的直流偏置电压，在此条件下减小发射信号的功率并不能显著减小拖尾信号；另外，CMUT器件的输出电流很小，在信号提取电路前添加负载会导致提取信号的能力降低，因此前两种方法对于此器件来说适用性较低。综合来看，可以采用叠加法来消除CMUT的拖尾信号。

本文首先介绍了CMUT传感器的工作原理，计算了CMUT传感器的集中等效参数，建立了CMUT的集中参数等效模型，利用该模型分析了CMUT的振动情况，确定了最佳的叠加策略，通过理论仿真与声学实验的对比，验证了本方法的有效性。

1 CMUT的工作原理[8]

CMUT的结构如图1所示，单个敏感单元的结构从上至下分别为上电极、单晶硅振膜、空腔、绝缘层和基底。其中，附着在单晶硅振膜上的金电极和底层的高掺杂硅基底构成了一个平行平板电容。工作时，需要预先在CMUT的平行平板电容两端外加一个直流偏置电压。在两端电场力的作用下，振膜发生形变，并且在单晶硅振膜弹性恢复的作用下，使振膜中形成一定的预紧力。CMUT有两种工作模式，分别是发射模式和接收模式。当工作在发射模式时，外加一个脉冲激励，CMUT振膜的平衡状态将会被打破，敏感单元的上极板会做自由阻尼振动，从而向外界发射超声波；当工作在接收模式时，空气中的超声波作用在振膜表面引起空腔内外压强差，使振膜在外界声波的作用下振动，导致电容的电荷量发生改变，从而在回路当中形成电流，通过提取这个电流信号就可以计算出空气中的声波信号。

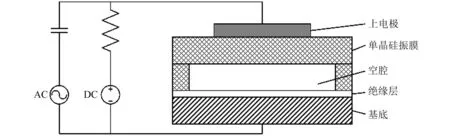
图1 CMUT结构图Fig.1 Structure schematic diagram of a CMUT

CMUT敏感单元的结构参数主要有振膜的半径、振膜厚度和空腔厚度，通过振膜结构参数的设置可以获得所需的工作频率。为获得更佳的性能，通常会将数量众多的CMUT敏感单元组成一组阵列，从而使发射信号的强度和接收灵敏度更强。在CMUT实际的使用中，一般是使用自发自收的工作模式，在CMUT激发出超声波之后立刻进入到接收模式，接收从空气中传回的反射信号。

2 CMUT的弹簧-质量-阻尼等效模型

弹簧-质量-阻尼模型是分析振动系统的有效的简化模型，通过对该模型的分析可以得到系统的振动函数等结果[9]。本文将会从CMUT的振动方程入手，通过计算CMUT敏感单元的等效集中参数来建立CMUT的弹簧-质量-阻尼等效模型。为建立这样的等效模型，需要求出CMUT的等效质量m，等效弹性系数k和等效阻尼系数ξ。为计算这些等效参数，将CMUT的一个敏感单元看成是周边固支的圆形薄板[10]，计算圆形薄板的平均位移。假设作用在薄板的载荷是均匀分布的，那么在考虑标准大气压和振膜上的直流静电力的条件下，作用在薄板上的载荷为

(1)

式中：a为振膜的半径；FeDC为极板间的直流静电力;Patm为标准大气压强。

图2 弹簧-质量-阻尼模型示意图Fig.2 Schematic diagram of the spring-mass-damper model

忽略振膜最上层的金电极，将整个振膜看作是半径为R，等效刚度为D的圆形薄板，则在均匀载荷下，薄板的挠度方程为[11]

(2)

式中：等效刚度D由式(3)给出

(3)

式中：E为薄板材料的杨氏模量；σ为材料的泊松比。

对式(2)积分求得圆形薄板的平均形变。

(4)

从式(4)中可以看到，圆形薄板的平均形变量是圆形薄板上形变最大值的1/3。薄板的形变是由于作用在薄板平面上的均匀载荷和薄板上的弹性恢复力共同造成的，因此通过薄板的平均形变可以得到薄板的等效弹性系数为

(5)

根据文献[12]得知，周边固支圆形薄板的振动频率为

(6)

式中：μ为0阶柱贝塞尔函数的根植，可以通过查表得知；h为薄板厚度；ρ为薄板的体密度；σ为薄板材料的泊松比。

根据等效弹性系数和等效振动频率可以计算出周边固支的圆形薄板的等效质量为

(7)

弹簧-质量-阻尼模型中还需要的一个参数是阻尼系数。阻尼是一个和质量块振动速度有关的参数，在弹簧-质量-阻尼系统中的弹性势能和动能最终都被阻尼损耗掉。在本模型中，我们可以把等效阻尼近似看成圆形平板的辐射声阻抗。这是由于，在激励信号结束之后，振膜的能量转化过程主要是弹性势能转化为声能，因此等效阻尼系数即为

ξ0=Zairπa2

(8)

式中：Zair为空气介质的辐射声阻抗。

3 模型仿真

上一节建立了CMUT的弹簧-质量-阻尼集中参数模型，从而可以写出模型的动力学微分方程

(9)

式中：u为振元薄板相对于初始位置的弹性形变；Fe为极板间的电场力。由于极板间所加的电压信号由直流部分和交流部分组成，因此极板间的而电场力可以表示为

(10)

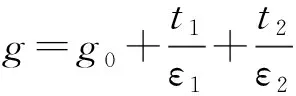
(11)

其中，

g′=g-uatm-uDC

(12)

在标准大气压和直流偏置的条件下有

kuatm=APatm

(13)

kuDC=FeDC

(14)

将式(11)、式(13)、式(14)代入式(9)中整理得

(15)

由于VAC是一个矩形脉冲信号，而矩形脉冲又可以看成是两个阶跃信号的叠加，因此计算时可以先把等号右边可以看成是一个阶跃信号，uAC可以看成是一个二阶系统的阶跃响应。

其中，ξ为二阶标准式的阻尼系数，其值等于

(16)

二阶系统的自然频率为

(17)

由于声介质的密度很小，因此等效集中参数模型实际上是一个欠阻尼(ξ<<1)的二阶系统。可以写出系统的阶跃响应函数为

(18)

其中,

(19)

(20)

利用MATLAB对CMUT的振动模型进行模拟，在实际使用的过程中，CMUT的激励信号一般是使用一个短脉宽的矩形脉冲激励，因此CMUT的激励信号实际上可以视作是两个阶跃信号的叠加。矩形脉冲信号的脉冲宽度长短会影响到拖尾信号的拖尾长度以及发射能量的强度。如图3所示，当脉冲宽度增加时，拖尾长度和能量会周期性的增大与减小，这是由于矩形脉冲信号可以看作是两个阶跃信号的叠加，两个叠加信号的相位差会影响到总信号呈现出周期的增强和减弱。

图3 激励脉冲宽度和盲区范围与信号能量的关系Fig.3 The relationship diagram of the excitation pulse width and the blind distance and the magnitude of the signal

图4(a)是脉冲宽度为2 μs的矩形脉冲所激励出的振动信号，此时脉冲信号的能量是最强的，同时拖尾长度也是最长的。CMUT在0时刻激励结束，需要240 μs振动的幅值才降至最大振幅的十分之一，声速在空气中是340 m/s，因此得到此情况下传感器的测量盲区为8.1 cm。图4(b)是将与原激励信号相位相差半周期(2 μs)的等幅叠加信号相叠加的效果。叠加信号的脉冲宽度和原激励脉冲相同。叠加等幅信号之后，信号的震荡情况极大的被改善，盲区范围减小至0.2 cm。因此，从理论上证明了，叠加法可以有效的抑制拖尾信号的产生。

图4 CMUT传感器的拖尾信号和叠加法处理后的信号对比Fig.4 Comparison of the ultrasonic tailing before and after dealing with the superposition method

4 实验结果

4.1 实验连接图

为验证理论的结果，本文设计了实验对比叠加法前后的拖尾信号的情况。实验中使用的CMUT传感器采用硅键合工艺加工而成，传感器的实物图如图5所示。

图5 CMUT传感器实物图Fig.5 Photograph of the CMUT

传感器上一共有256个敏感单元，每个敏感单元的振膜半径为400 μm，敏感单元之间的间隔200 μm，理论计算得到的敏感单元的自然频率为256 kHz，但是由于加工的工艺因素会导致敏感单元的实际自然频率和理论频率不相同。敏感单元的实际自然频率可以通过阻抗分析仪测得，实际值为230 kHz。

实验的连接框图如图6所示，不同于传统的压电晶片做的超声传感器，CMUT工作时需要外加一个高电压的直流偏置，使薄板出于张紧的状态。激励信号由FPGA产生，经驱动电路产生一个低电平脉冲，然后通过一个直交流耦合模块耦合至CMUT传感器。在激励信号结束后，CMUT传感器进入接收模式，通过信号提取电路来提取CMUT中的电流信号。信号提取电路由限伏电路、跨阻放大电路和滤波电路组成，通过信号采集卡将接收到的信号保存至上位机中。

图6 实验连接图Fig.6 Experiment connection diagram

4.2 激励信号

实验中FPGA输出的激励信号是一个2 μs的短脉宽矩形波信号，经驱动电路放大后幅值增大为12 V。当不加反向叠加信号时，示波器显示的信号如图7(a)所示。可以看出，在激励结束后，电路中的拖尾信号长度为205 μs，最大幅值超过20 mv，盲区范围为7.0 cm。在发射一个周期后施加一个反相叠加信号，从图7(b)中可以看出拖尾部分被极大的削弱，削弱后的拖尾信号最大幅值不超过2 mv，盲区范围减小至0.8 cm。盲区范围被缩小了88.6%。

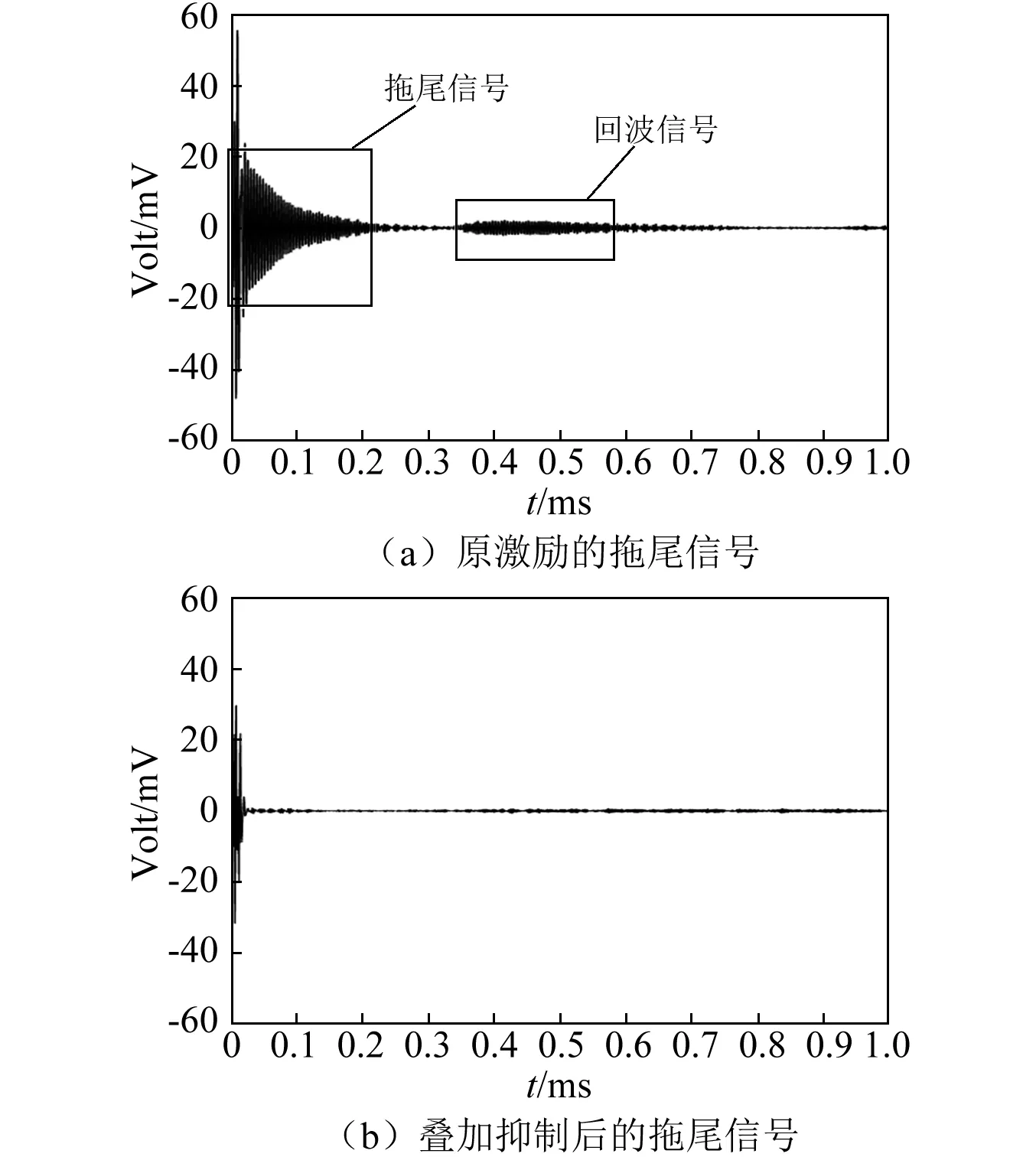
图7 CMUT传感器拖尾信号前后对比Fig.7 Comparison of the ultrasonic tailing before and after dealing with superposition method

由于空气密度很小导致其声阻抗和CMUT传感器有较大的不匹配，因此超声波从空气中传导至CMUT表面引起振膜振动时，会有很大一部分能量通过反射而损失掉。如果CMUT在发射模式下发射的超声波能量过小，那么在接收模式下就无法正常检测到回波信号。事实上，拖尾信号的本质是振膜的自由阻尼振动，消除拖尾信号会导致CMUT传感器发射出去的声波能量降低，回波信号无法被检测到。为使得信号能量足以被检测，需要保证一定时间长度的自由阻尼振动，也就是脉冲激励信号与反相叠加信号之间应该留下一定长度的时间间隔。图8表示了传感器发射的脉冲时间间隔和回波信号能量的关系。振膜自由阻尼振动的一个振动周期是4 μs，反相叠加信号和激励信号的时间间隔需要是半周期的奇数倍。从图中可以看出，时间间隔越长，CMUT在接收模式下检测到的回波信号也就越强，同时测量的盲区范围越大。这两个关系是彼此相矛盾的，因此需要根据实际测量情况动态的设置时间间隔长度。在时间间隔42 μs时，回波能量强度小于-1 dB，此时间间隔对应的振动的周期数为10个半周期，实验中选择的时间间隔为42 μs，可以在保证回波能量的前提下，使盲区较小，此时理论盲区长度为1.4 cm。

图8 发射时间间隔和信号能量与盲区范围的关系曲线Fig.8 The relationship diagram of the internal time and the signal energy and the blind distance

拖尾信号是呈指数衰减的，在振动十个周期后拖尾信号的幅值会大幅度降低，如果此时施加的反相激励脉冲宽度和原始激励的脉冲宽度相同，则会由于过度消除而产生同反相信号同相的拖尾信号。图9表示了理论计算的拖尾信号的幅值衰减曲线，图10表示了矩形脉冲的脉冲宽度和振膜振动最大幅值的关系曲线。从图9中可以看出被2 μs脉宽的矩形脉冲所激励的振动信号，在十个半周期之后的振动幅值是1.27 nm，此时如果反相叠加信号的激励脉冲宽度同样是2 μs，理论计算得到的叠加信号将会如图11(a)，从图中可以看出，由于过度消除而导致拖尾信号依然存在。所以应当通过减小反相叠加信号的激励脉冲宽度来使该信号所激励出的最大振动幅值和1.27 nm相匹配，才能达到最佳的消除效果。通过图10可以看出将叠加信号的脉宽减小至0.9 μs时，最大振幅为1.27 nm。此时FPGA在0时刻发射2 μs的激励脉冲信号，然后在42 μs的时刻发射0.9 μs的反相叠加脉冲信号，理论计算的叠加信号如图11(b)显示，可以看出拖尾信号完全被消除。在此期间CMUT传感器做自由阻尼振动，从而保证发射声波的能量。

图9 信号幅值随时间的衰减Fig.9 Attenuation of the signal over time

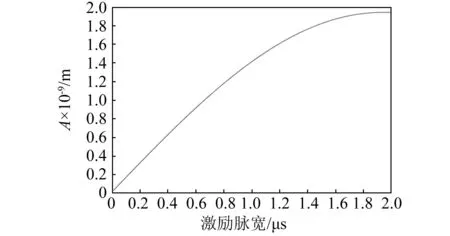
图10 信号最大幅值和激励脉宽关系Fig.10 The relationship of the maximum amplitude of the signal and the pulse width

图11 2 μs，0.9 μs脉宽的拖尾信号对比Fig.11 Comparison of the tailing signal under 2 μs and 0.9 μs of pulse width

4.3 CMUT直流电压和盲区范围的关系

CMUT工作时需要在振膜的两侧施加一个直流电压，通过这个直流电压来给CMUT器件提供预紧力，以提高其检测的灵敏度。下图表示了直流偏置电压和测量盲区的关系，从图12中可以看出，偏置电压越小CMUT的盲区范围越小。但是，偏置电压也会影响到CMUT发射信号的能量和接收灵敏度，张慧等的研究显示，偏置电压越大CMUT的发射信号的能量和接收灵敏度都会提高。理论上来讲，在满足信号能量要求的前提下可以通过减小直流偏置电压来减小盲区范围，但是实际使用当中，为获得更佳的信号，应在CMUT能承受的电压范围内尽可能高的增加CMUT的偏置电压。出于安全和保护器件的考虑，实验中加载的直流偏置电压为90 V。

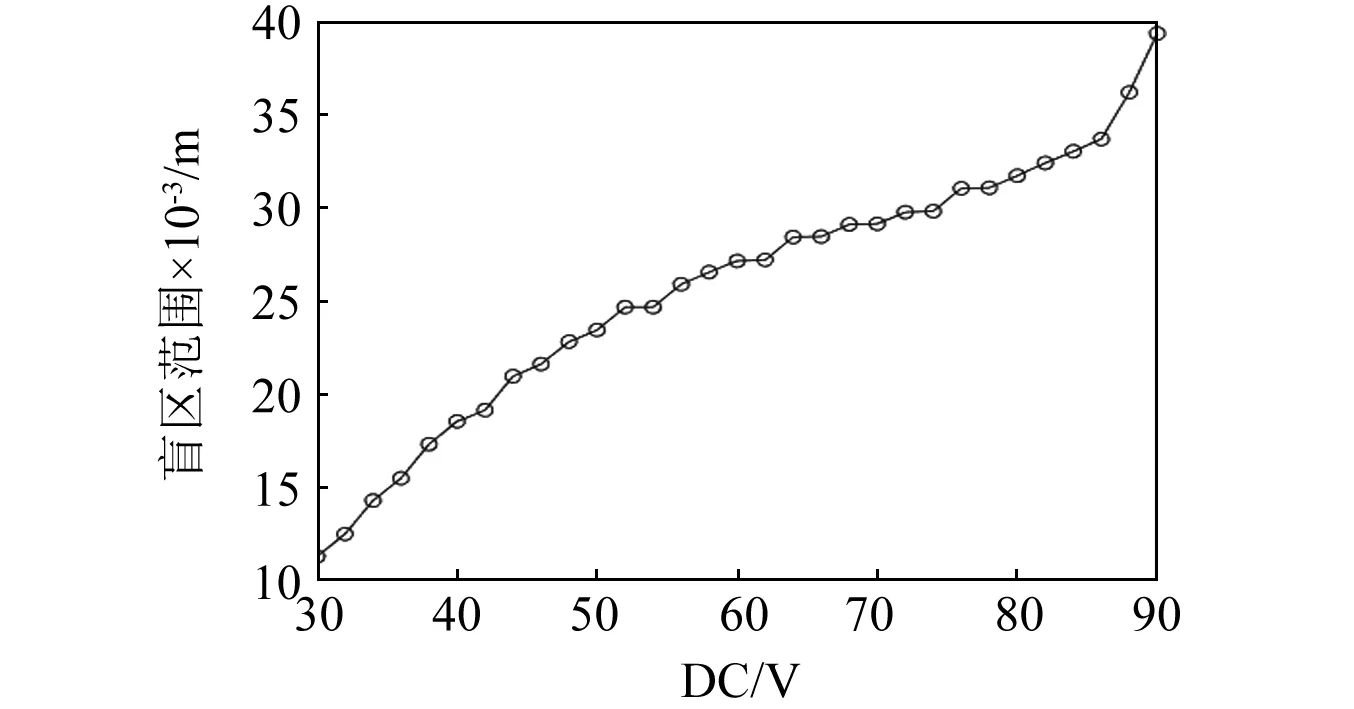
图12 CMUT直流电压和盲区范围的关系Fig.12 The relationship of the blind distance and the DC voltage

4.4 近距离障碍物检测

在CMUT传感器前5 cm处摆放了一块3.2 cm的铁质立方体障碍物，通过发射pulse-echo超声波来完成对障碍物的测距。CMUT传感器加载的直流偏置电压大小为90 V，矩形脉冲激励电压幅值为12 V，脉冲宽度为2 μs，反相叠加脉冲的电压为12 V，脉冲宽度为0.9 μs。

图13(a)表示了被淹没在拖尾信号中的回波信号，可以看到图中很难从拖尾信号中提取出回波信号；图13(b)表示采用了叠加法消除拖尾后的回波信号的情况，可以清晰地识别出回波信号，从图13(b)中得到在42 μs的时间间隔的条件下，实际盲区范围为2.9 cm，

图13 近距离障碍物回波信号对比Fig.13 Comparison of the echo signal before and after dealing with the superposition method

相比理论盲区范围存在1.5 cm的误差，相对于未采用叠加法所造成的7.0 cm的盲区范围，该方法减小了58.6%；在0.147 ms处接收到回波信号，计算出障碍物和CMUT传感器表面的距离为5.0 cm，和实际距离相符。从而可以得到结论，反相信号叠加激励法可以有效的缩短盲区范围，提高系统的检测能力，对于空气中近距离的障碍物检测有着重要意义。

5 结 论

本文针对CMUT传感器在近距离障碍物测距中盲区的问题，提出了一种有效抑制拖尾信号的方法。结合CMUT器件本身的特性，分析了不同脉冲宽度的矩形脉冲激励信号下CMUT传感器的响应以及相应的回波信号的能量，并以此为根据设计了激励信号的激励策略来实现对盲区控制和回波信号能量的兼顾。通过仿真可以看出，该方法对消除拖尾信号具有可行性，并且通过设计实验验证了方法的有效性。实验虽然已经实现针对拖尾信号的消除以及近距离障碍物的识别，但是对于盲区范围的消除只有64.2%，最终的方案依然存在2.9 cm的盲区。这是由两方面限制所造成，其一是空气中应用的CMUT传感器需要保证回波信号的能量，其二是实验条件的限制对叠加信号的精度控制不佳。后期可以通过设计驱动模块，增强CMUT传感器发射功率以及优化信号产生模块来完成对此问题的优化。