风速对水线及斜拉索振动的影响
王 剑,毕继红,何旭辉,关 健,乔浩玥
(1. 天津城建大学 天津市土木建筑结构防护与加固重点实验室,天津 300384;2.天津大学 建筑工程学院, 天津 300072;3.中南大学 土木工程学院桥梁工程系,长沙 410000)
随着现代斜拉桥跨径的不断增大,斜拉索越来越长、刚度和阻尼越来越小,导致其在特定风速及降雨条件下产生风雨激振现象。自1988年Hikami等[1]首次观测到风雨激振现象以来,研究人员对风雨激振的机理进行了大量的研究,并认识到拉索表面水线的形成和振荡是风雨激振的主要原因。对此Lemaitre等[2-3]等将滑移理论应用到风雨激振研究中,用风压力和风摩擦力来表示气流对水膜的作用,模拟水平静止拉索表面上的水线形成。许林汕等[4]考虑拉索运动对水膜形态变化的影响,根据已有研究成果假设拉索的运动规律,建立液固耦合模型研究水线的运动规律。Taylor等[5]则运用Lemaitre模型,通过数值求解得到随时间变化的风压力系数和风摩擦力因数,建立气液耦合模型分析水平静止的拉索表面上的水线运动规律。毕继红等[6-7]等将滑移理论和单质点运动理论结合,建立了气液固三相耦合的风雨激振模型。
国内外研究人员通过一系列的现场观测和风洞试验研究,发现在降雨强度为小到中雨的条件下,斜拉索仅在一定的风速范围内发生风雨激振现象,而风速过大或过小均不会出现,即风雨激振有“限速”的特点。现阶段关于风雨激振的起振风速区间的研究大多以风洞试验为主[8-9],理论分析方面的研究较少,特别是从水线运动角度的研究就更少。对此,本文对气液固三相耦合模型的数值计算过程进行改进,采用有限差分法求解水膜运动方程,并且应用有限元软件COMSOL求解随时间变化的风压力系数和风摩擦力因数,在保证计算精度的同时大幅度提高计算效率;在此基础上,研究风速变化对水线运动及斜拉索振动的影响,分析风雨激振的产生机理。
1 模 型
图1所示的半径为R、倾角为α(0°≤α≤90°的斜拉索,受重力和水平方向风的共同作用,风速大小为U0,风偏角为β(0°≤β≤90°)。
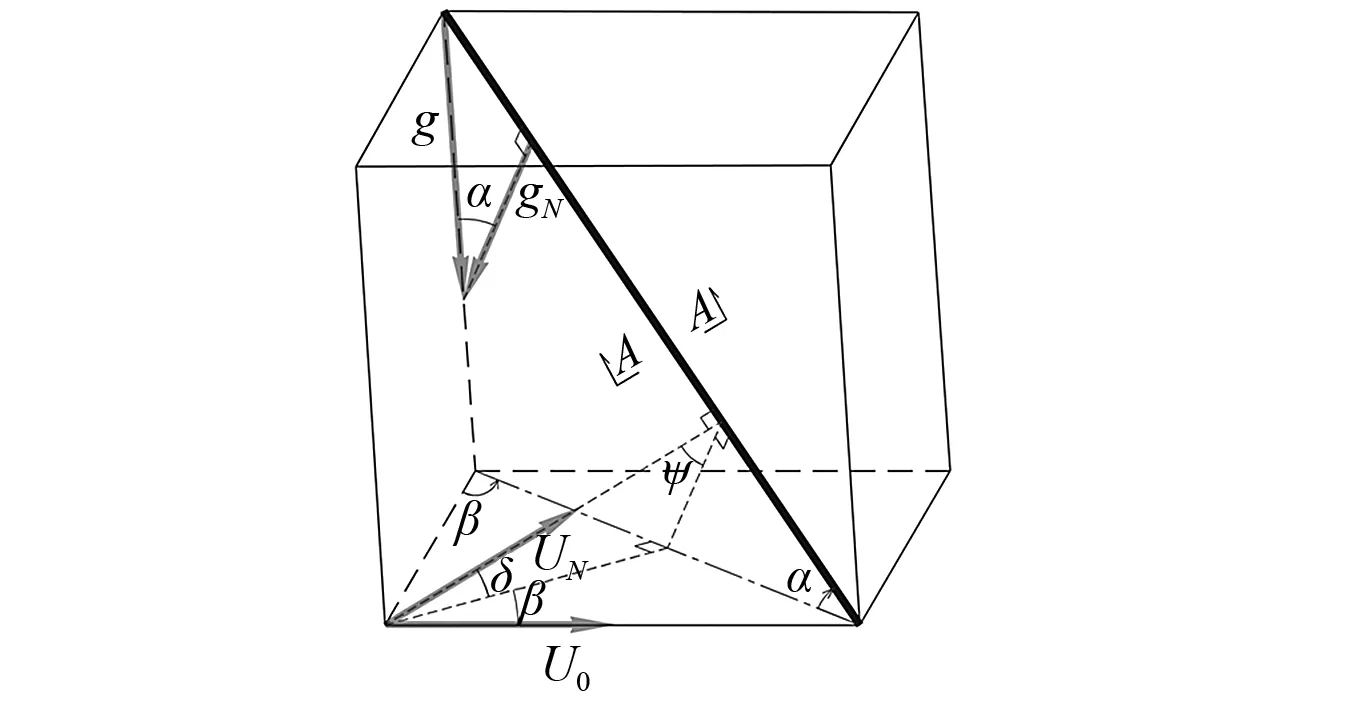
图1 斜拉索空间位置Fig.1 Spatial position of stay cable
取斜拉索任一横截面A-A为研究对象,如图2所示。对拉索的二维模型进行研究,忽略重力在拉索轴向方向的影响。
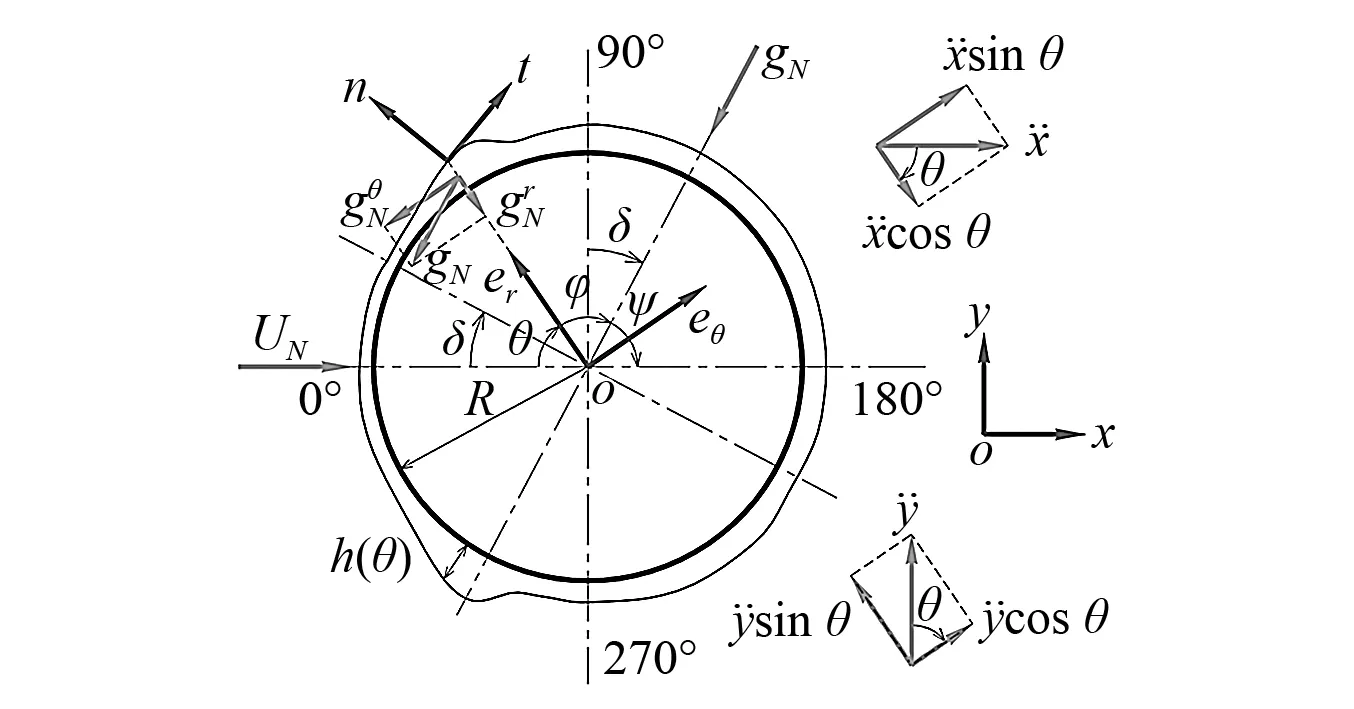
图2 斜拉索表面水膜受力Fig. 2 Force of water film around cable
根据滑移理论,假设拉索表面存在一层连续的水膜,两自由度无量纲化的水膜运动方程可表示为
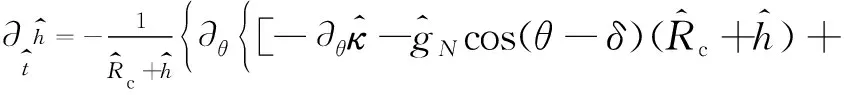
(1)
其中,
(2)
式中:t为时间;μ为水的动力黏度系数;γ为水在空气中的表面张力系数;h为水膜厚度;Rc为拉索半径;M为单位长度拉索的质量;ρg和ρ分别为空气和水的密度;κ为水膜表面的曲率;n和t分别为水膜与空气交界处的法向向量和切向向量;σg分别为空气的应力张量;pg为水膜表面所受的空气压力。
斜拉索在横风向和顺风向的振动方程为
(3a)
(3b)
其中,
(4a)
(4b)
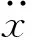
2 数值求解
2.1 有限差分格式
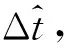
(5)
其中,
(6a)
(6b)
(6c)
2.2 风压力系数Cp与风摩擦力因数Cf
水膜运动方程中的风压力系数Cp和风摩擦力因数Cf是影响水膜运动的关键参数。在已有的研究中,毕继红等人采用Fluent软件获取表面带有不同形状水膜的斜拉索的Cp和Cf,计算时间很长,效率极低,仅能获得前20 s的运动状态;而Gu等[10]的试验数据表明,从试验开始到风雨激振真正形成,需要数十秒甚至上百秒的时间。对此,本文采用有限元软件COMSOL计算随时间变化的风压力系数和风摩擦力因数,大幅提高了计算效率和计算稳定性。
本文应用COMSOL软件计算时仍采用与原先相同的假设,即假设水膜所受的气流作用与干燥拉索表面所受的气流作用相同。每一时间步内均根据上一步计算得到的水膜形状,将水膜考虑为固态,建立流场中的绕流障碍物,应用Spalart-Allmaras湍流模型,采用稳态计算此时刻的Cp和Cf。
设干燥拉索直径为d,计算区域及网格划分如图3所示。边界条件设置如下:
左侧进口处采用速度边界条件(u=UN,v=0);右侧出口处采用压强边界条件(p=0);上下边界处采用完全滑移边界条件;圆柱表面处采用无滑移边界条件(u=0,v=0)。
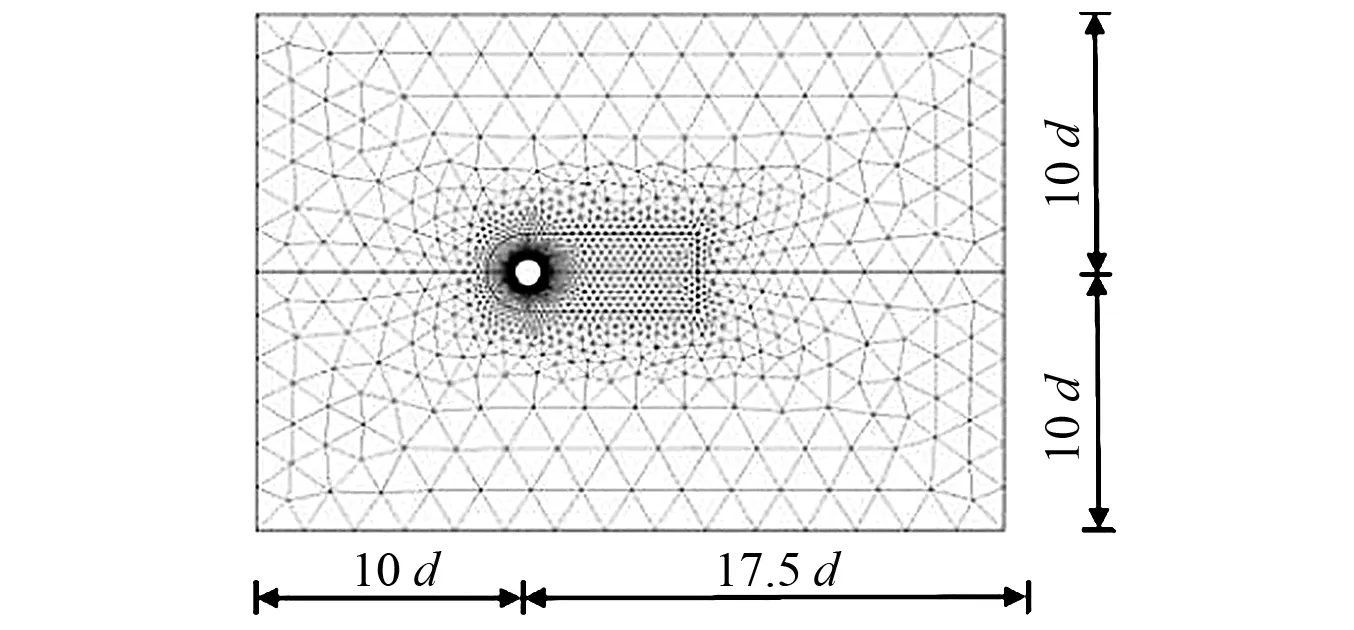
图3 流场网格划分Fig.3 Numerical grids of the flow field
将数值求解得到的风压力系数Cp和风摩擦力因数Cf与Fage等[11]的试验数据、Celika等[12]及Bi等的数值计算结果进行对比,考虑圆柱直径为0.16 m,风速为10 m/s的试验工况,如图4所示,应用COMSOL软件求解得出的结果与前人的研究结果非常接近,验证了数值方法的准确性。
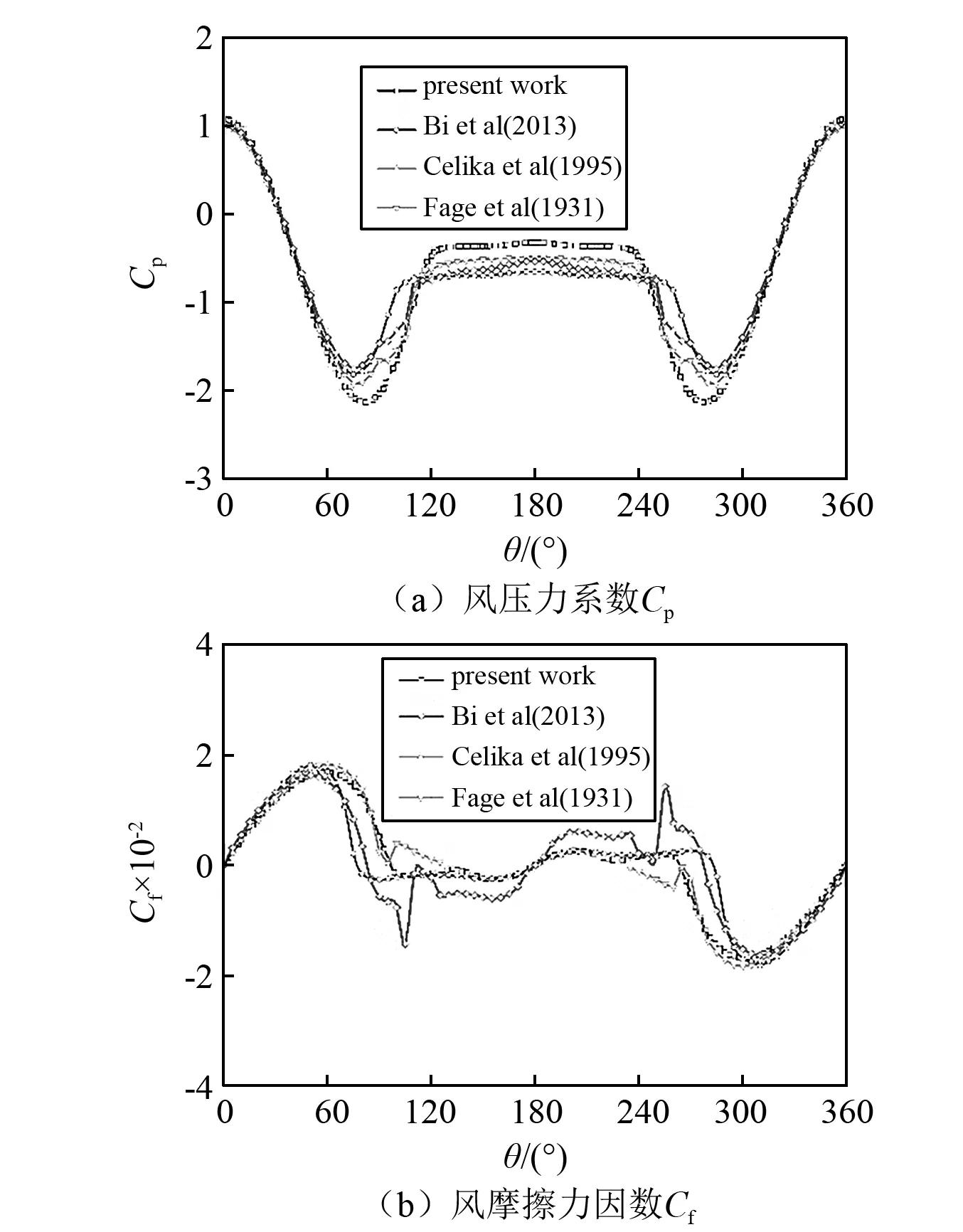
图4 圆柱表面风压力系数Cp和风摩擦力因数Cf的分布图Fig.4 Distribution of wind pressure coefficient Cp and friction coefficient Cf around cylinder
2.3 基本参数及数值计算工况基本
借鉴文献[13-14]中的风洞试验数据,基本参数选取如下:斜拉索半径0.05 m、倾角30°、自振频率0.952 Hz、线密度8.57 kg/m、阻尼比0.17%;拉索的初始位移、速度和加速度均为零;水膜的初始厚度为0.2 mm;水密度1.0×103kg/m3、水的运动黏性系数1.0×10-6m2/s、水在空气中的表面张力系数7.2×10-2N/m、空气密度1.225 kg/m3、空气的运动黏性系数1.51×10-5m2/s;风偏角22.5°,风速6.0 m/s,6.76 m/s,7.4 m/s,7.5 m/s,7.6 m/s,7.72 m/s,8.2 m/s,8.5 m/s,9.0 m/s,9.5 m/s,10.5 m/s,12.0 m/s,13.5 m/s。
参照已有的研究成果,在采用有限差分法求解水膜运动方程时,时间步长dt=1×10-5s,为保证拉索表面水膜的质量守恒,根据试验观测数据,假设水膜的最大厚度为1 mm;为使水膜在拉索表面连续分布,假设水膜的最小厚度为0.02 mm。
2.4 数值求解流程
水膜运动方程(见式(1))为四阶偏微分方程,拉索振动方程(见式(3))为二阶微分方程,采用差分法求解方程组,应用MATLAB软件进行数值计算并利用有限元软件COMSOL求解各个时间步不同水膜形态下的风压力系数Cp和风摩擦力因数Cf,基本流程如图5所示。
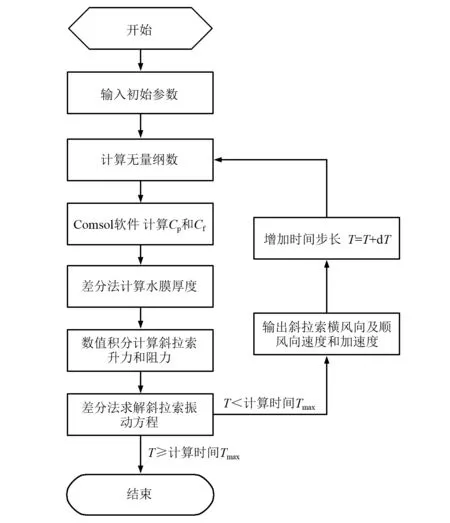
图5 数值计算流程图Fig.5 Flowchart of numerical calculation
3 数值计算结果
3.1 拉索振动响应
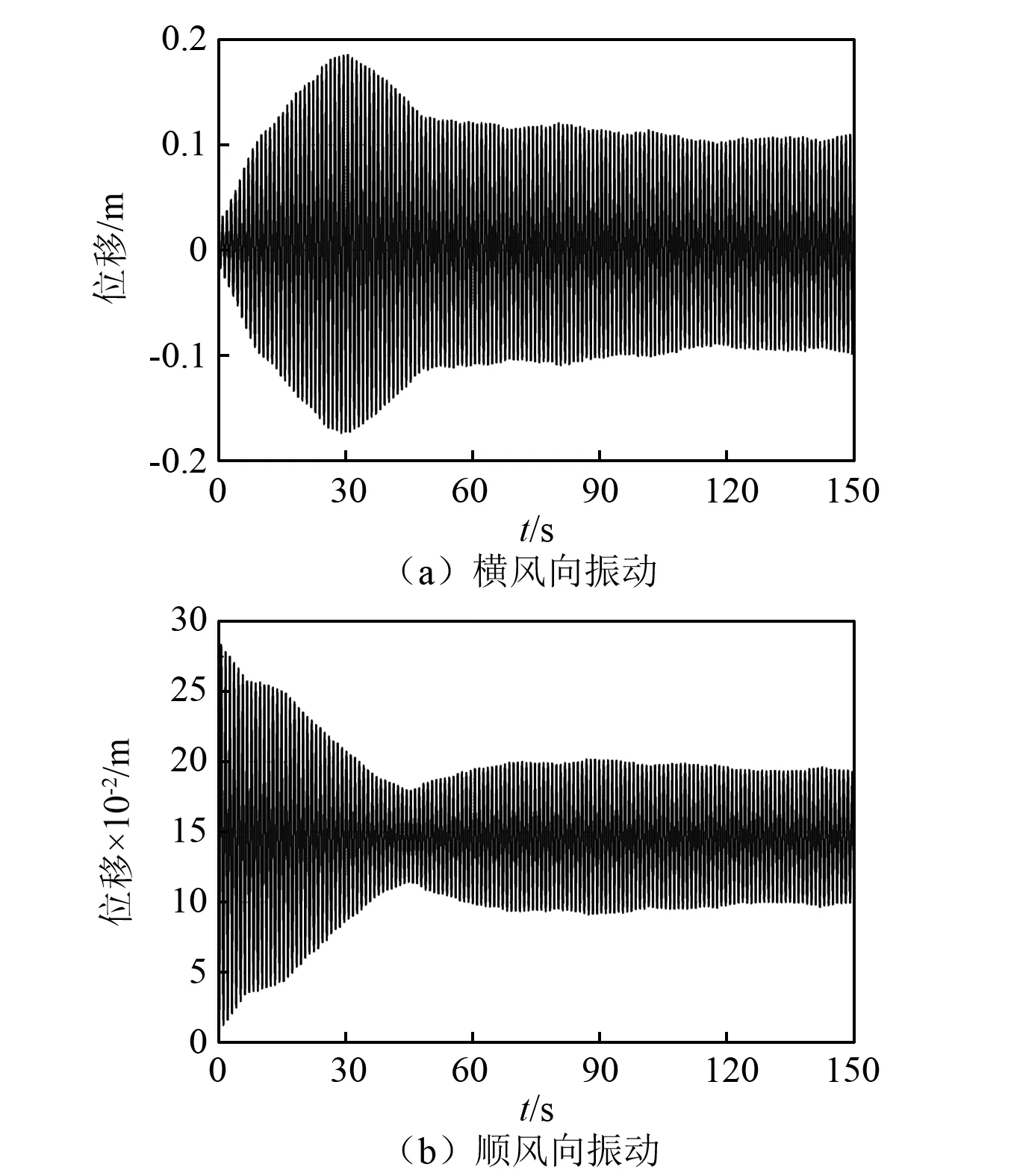
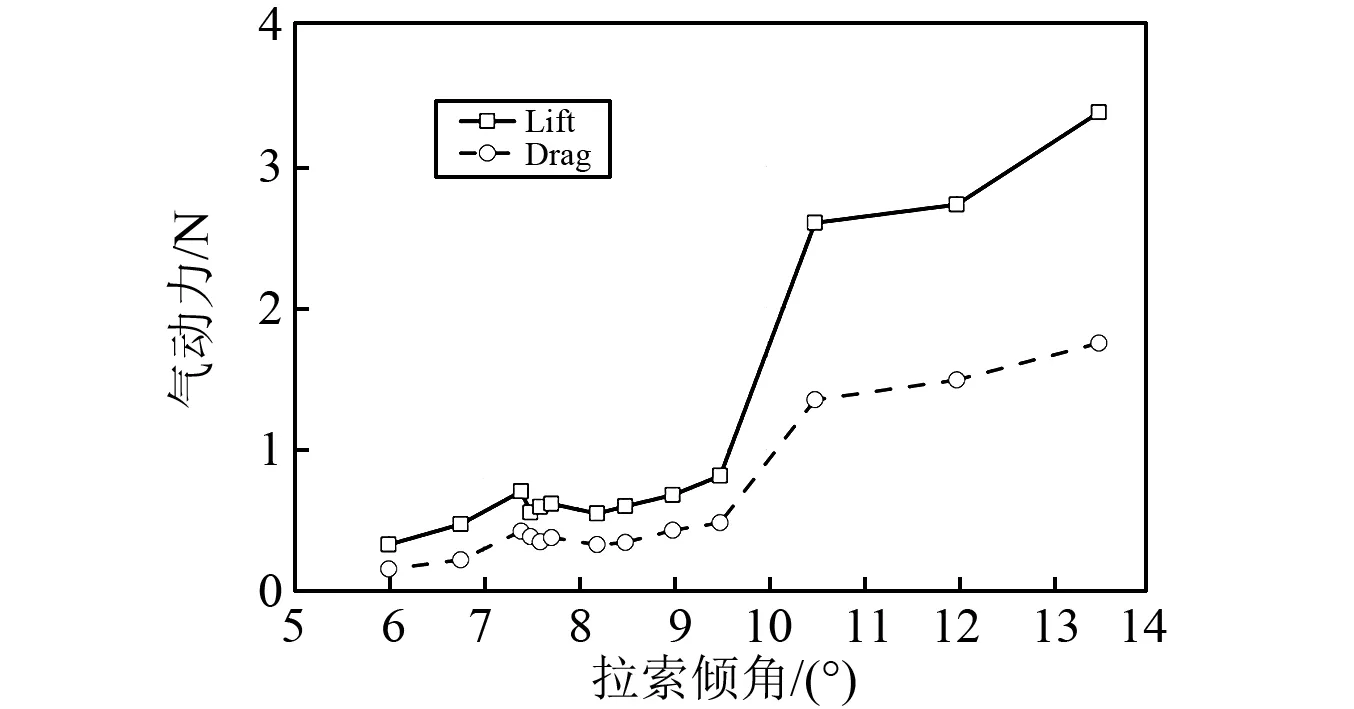
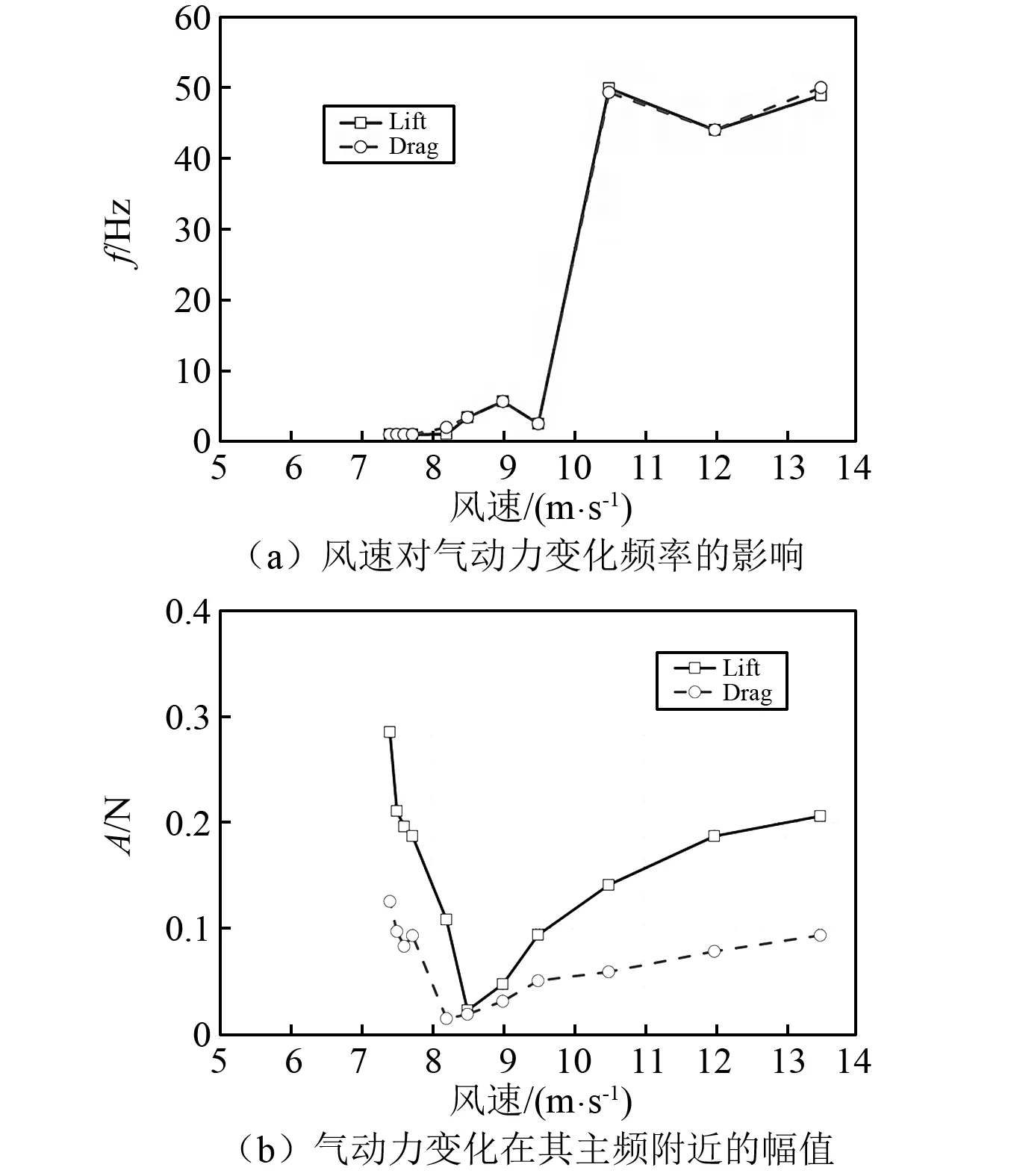
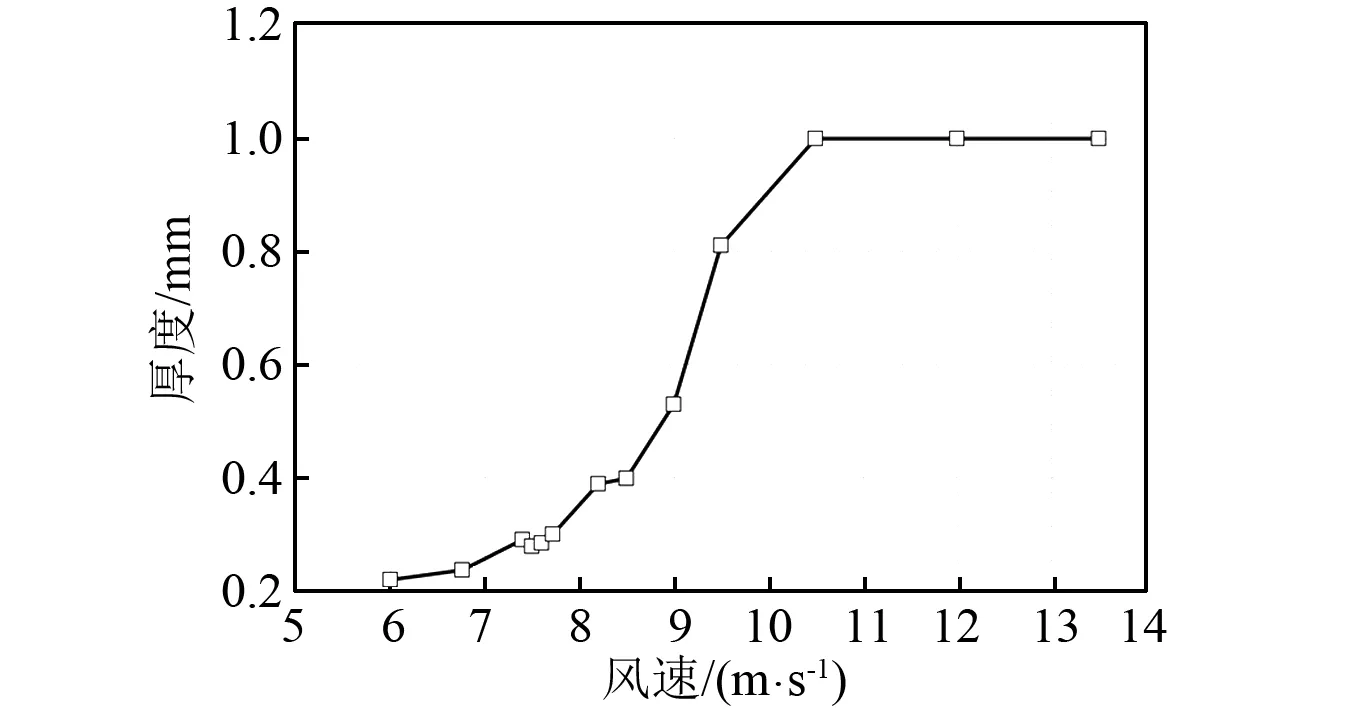
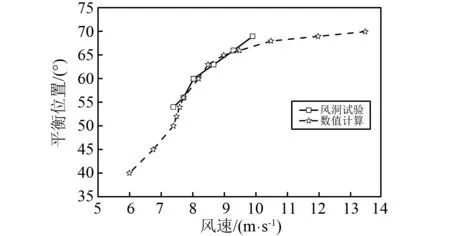
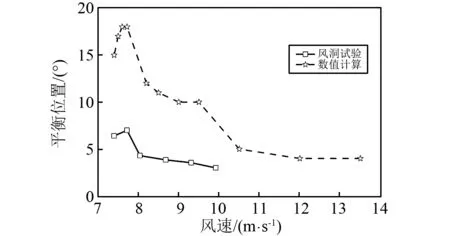
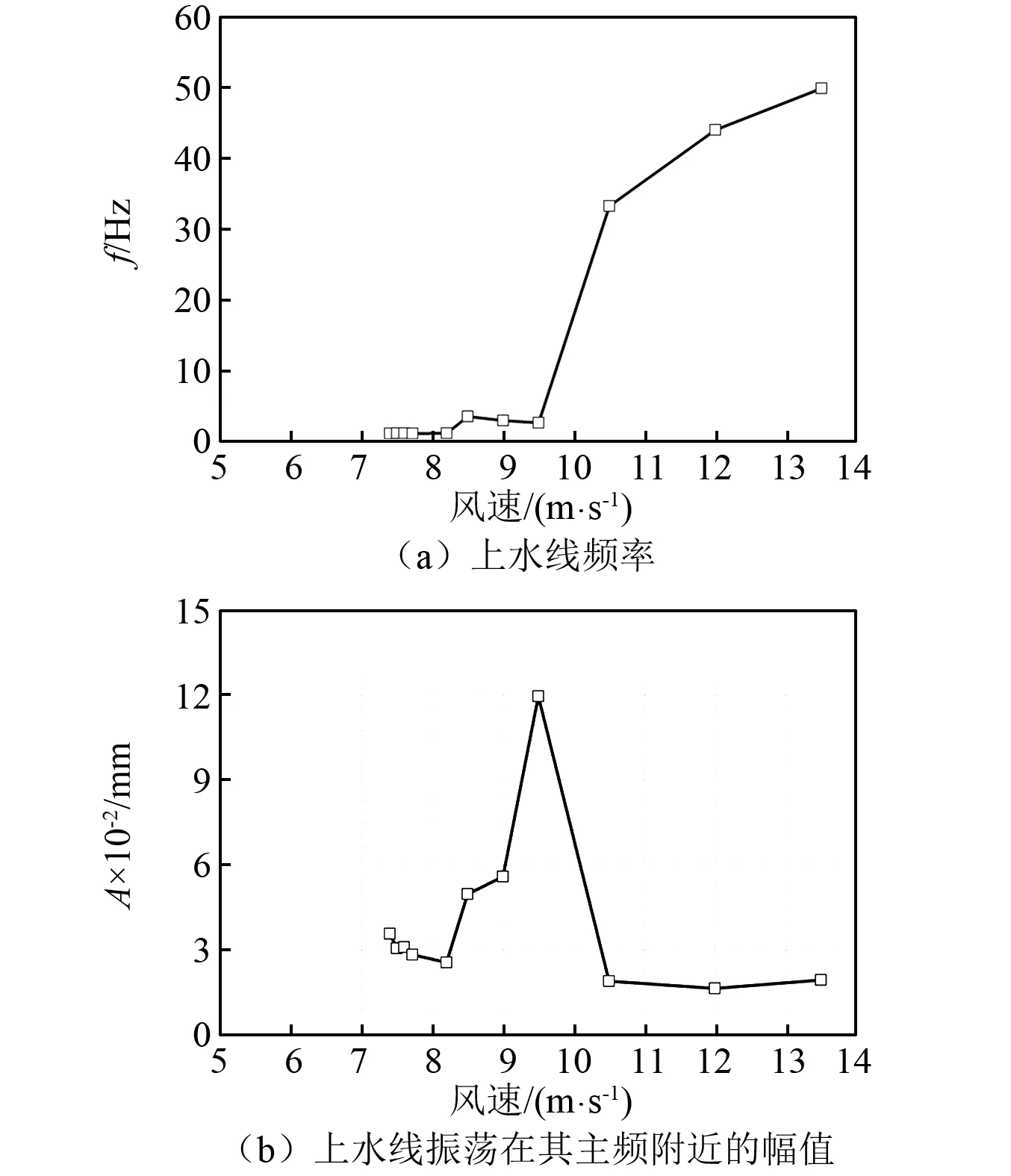
图6显示了各个风速工况下斜拉索的横风向及顺风向振幅变化。数值计算得到的起振风速区间是6.76 m/s 图6 风速对拉索振动的影响Fig.6 Influence of wind velocity on cable vibrations 图7为风速7.5 m/s下拉索在0~150 s内的振动响应。在0~29 s以内,拉索横风向振幅迅速增大,振幅达到0.19 m左右,如图6(a)所示;而后振幅迅速衰减,至50 s附近,振幅减至0.13 m;50~100 s内拉索振幅继续小幅减小,在100 s以后逐步趋于稳定,保持在0.10 m左右,与实验结果(0.09 m附近)相近,如图6所示。 7.5 m/s时拉索的顺风向振幅如图7(b)所示。初始时刻,拉索的顺风向振幅为0.14 m;前45 s内,拉索振幅迅速减小,最小值为0.03 m;之后小幅增大,72 s后逐渐稳定在0.05 m左右,近似等于拉索横风向振幅的一半,与现场观测结果相同。与前人的研究结论相一致,拉索在两个方向的振动均需要几十秒(50 s左右)的时间达到稳定振动状态,因此本文对各风速工况均进行了150 s的计算,选用100~150 s的计算结果进行分析研究。 图7 风速7.5 m/s时的拉索振动时程曲线Fig.7 Vibration responses of cable with wind velocities 7.5 m/s 各个风速工况下的拉索气动升力及阻力变化幅度曲线,如图8所示。随着风速的增加,升力和阻力在总体上均呈现出不断增大的趋势。但当风速处于6.76 m/s 对每一风速下拉索的气动力变化时程进行频谱分析,如图9(a)所示。绝大多数风速下升力和阻力的主频相一致。当风速较低(U0≤6.76 m/s)时,升力和阻力的变化均无明显的主频;当风速位于风雨激振的风速区间(6.76 m/s 图8 风速对气动力变化最大幅度的影响Fig.8 Influences of wind velocity on aerodynamic forces 图9(b)为拉索气动力在其主频附近的变化幅值与风速变化间的关系曲线。6.76 m/s 综上所述,决定拉索振动强弱的主要因素是气动力变化在拉索自振频率附近幅值,而非其整体的最大变化幅度。 随着风速从6 m/s增大至9.5 m/s,上水线的最大厚度不断增加,从0.22 mm逐渐增加至0.81 mm,且其增加的幅度越来越大;至10.5 m/s以上时,上水线的最大厚度达到计算假设的1.0 mm,如图10所示。上述趋势与拉索气动力最大幅度的变化趋势相近,说明上水线厚度对升力和阻力的变化幅度有显著影响。 从图11所示的各风速工况下的上水线振荡平衡位置可以看出,风速为6 m/s时的上水线中心位置大致在40°附近;随着风速的增大,上水线平衡位置不断向背风侧偏移;到13.5 m/s风速时移至约70°。文献[13]和文献[14]中的坐标系与本文数值计算时选取的坐标系相差90°,经坐标变换后进行对比,发现数值计算结果与风洞试验结果基本一致,如图11所示。 图9 不同风速拉索的气动力变化频谱分析Fig.9 Frequency spectrum analysis of aerodynamic forces with various wind velocities 图10 各风速工况下的上水线厚度Fig. 10 Upper rivulet thickness with various wind velocities 图11 各风速工况下的上水线振荡平衡位置Fig.11 Equilibrium positions of upper rivulet oscillations with various wind velocities 图12所示显示了各风速工况下的上水线振荡幅度。由于风速小于7.4 m/s时,上水线振荡幅度很小,故在此只研究风速大于7.4 m/s时的上水线振荡幅度。当风速位于风雨激振的风速区间(6.76 m/s 图12 各风速工况下的上水线振荡幅度Fig.12 Amplitudes of upper rivulet oscillations with various wind velocities 通过对各风速工况下的上水线位置处水膜厚度变化时程进行频谱分析(见图13),可以进一步研究水线运动与拉索振动间的相互影响。 图13(a)为上水线振荡频率与风速的关系,当风速较低(U0≤6.76 m/s)时,上水线厚度较小且基本无运动;当风速位于风雨激振的风速区间(6.76 m/s 图13(b)显示了各风速工况下上水线位置处的水膜厚度变化在其主频附近的幅值。当风速位于风雨激振的风速区间(6.76 m/s 对比图6所示的拉索振动与图10、图13所示的水线振荡,可以看出影响拉索振动强弱的主要因素是水线的振动频率而非其厚度,只有当水线振荡频率与拉索自振频率相近时,才会使得拉索气动力的频率接近拉索自振频率,产生风雨激振现象;此时,拉索的振动幅度与拉索自振频率附近上水线振荡的强弱有密切联系。 分别选取风速6.0 m/s、7.72 m/s、9.0 m/s和13.5 m/s的水膜厚度时程变化用来分析研究水线运动与拉索振动间的相互影响,如图14所示。 图13 不同风速拉索的上水线频谱分析Fig.13 Frequency spectrum analyses of upper rivulets with various wind velocities 6.0 m/s风速下,上、下水线均保持稳定状态,振荡幅度很小;7.72 m/s风速下,上、下水线均做周期性的环向振荡,周期大致与拉索的自振周期一致,且上水线的振荡幅度远大于下水线;9.0 m/s风速下,上、下水线亦在振荡,但其周期显著减小,远小于拉索自振周期;至13.5 m/s风速时,上水线振荡的周期性已不再明显。 图15显示了风速6.0 m/s,7.72 m/s,9.0 m/s和13.5 m/s时上水线位置处水膜厚度变化的频谱分析。 风速6.0 m/s时,由于上水线基本保持稳定状态而无明显的振荡频率,导致拉索气动力变化幅度很小且无明显主频,因此拉索振动很弱,不会产生风雨激振现象;风速7.72 m/s时,上水线的环向振荡显现出明显的周期性特征,主频为0.98 Hz,接近拉索的自振频率,导致拉索气动力亦发生同频率的周期性变化,从而引发拉索的大幅度振动;当风速为9.0 m/s时,上水线的振荡幅度明显增大,导致气动力变化的幅度亦明显增大,但水线振荡主频为2.82 Hz,远大于拉索自振频率,致使拉索气动力变化频率亦远大于拉索自振频率,拉索振幅明显减小;当风速增大至13.5 m/s时,上水线的振荡频率已增大至49.98 Hz,远远大于拉索自振频率,没有出现风雨激振现象。因此,只有当一定风速范围内,上水线振荡频率与拉索自振频率相近时,才会导致拉索发生显著的风雨激振现象。 图14 拉索表面水膜厚度时程变化Fig.14 Temporal evolution of water film thickness 图15 上水线频谱分析Fig. 15 Frequency spectrum analysis of upper rivulet 本文考虑拉索横风向和顺风向的振动对水膜形态变化的影响,将滑移理论和两自由度振动理论相结合,建立风雨激振时拉索和水膜耦合的理论模型;通过数值计算得到了不同风速工况下150 s的拉索振动响应、气动力变化和水线运动情况,计算结果与人工降雨条件下拉索节段模型的风洞试验数据吻合;在此基础上分析风速对水线运动及拉索振动的影响,得出以下结论: (1) 由两自由度模型得到的拉索振动响应、气动力及水膜形态变化规律均与风洞试验相近,验证了模型及数值模拟方法的准确性。 (2) 150 s的拉索振动时程表明拉索在两个方向的振动均需要经过几十秒的不稳定期后才会产生风雨激振现象,与已有的现场观测结论相一致,显示出提高数值计算效率的必要性。 (3) 随着风速的增大,水线厚度逐渐增加,上水线环向振荡的中心位置逐渐向背风侧偏移,但拉索只在一定风速范围内发生大幅度振动,且其横风向振幅接近顺风向振幅的两倍。 (4) 只有当风速处于特定范围内时,上水线在拉索表面环向振荡的幅度最大,且其周期性振荡的频率接近拉索自振频率,导致升力、阻力发生相近频率的周期性变化,引发拉索在横风向和顺风向发生大幅度振动;而当风速过大或过小时,水线运动及升力、阻力变化的频率与拉索自振频率相去甚远,导致拉索振动明显减弱。因此,上水线与拉索之间的共振是导致拉索发生风雨激振的主要原因之一。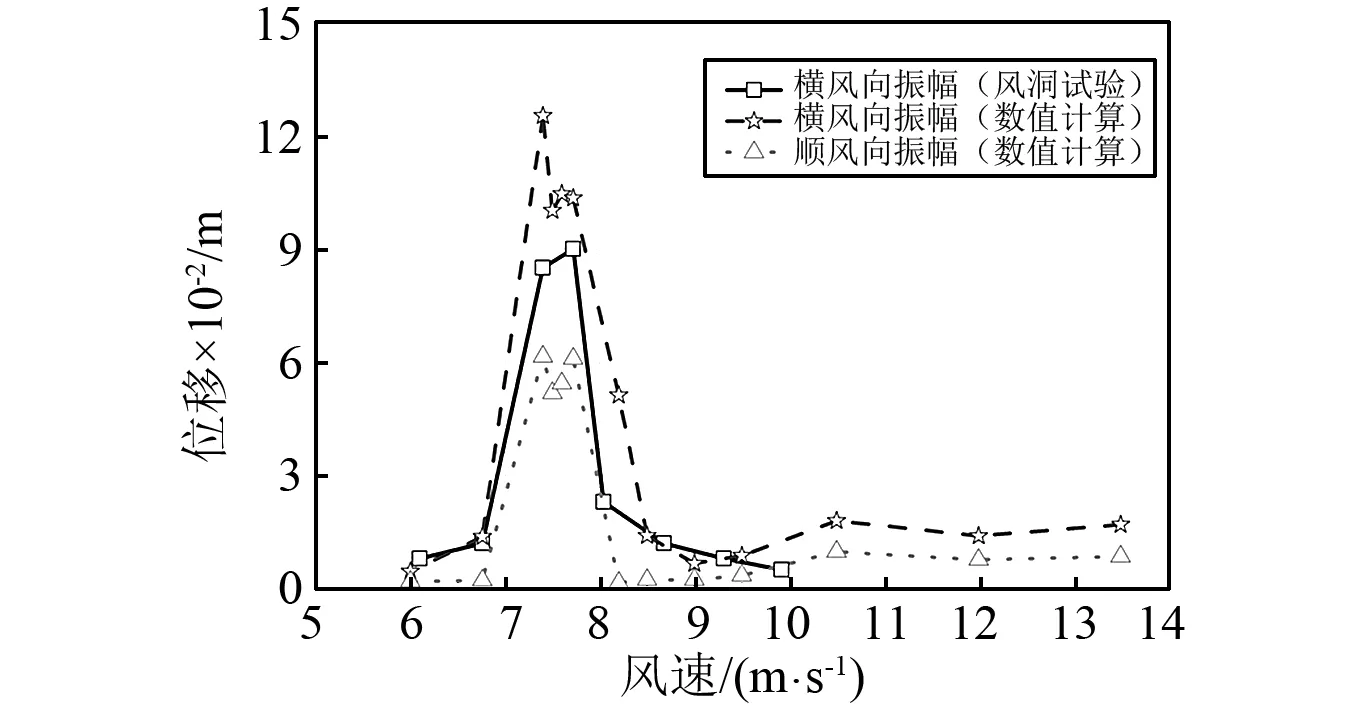
3.2 拉索气动升力和阻力
3.3 水线形态及其运动特征


4 结 论

