基于量子Hadamard变换的滚动轴承振动信号分析方法

王怀光，陈彦龙，杨望灿，王 强

(1. 军械工程学院 七系，石家庄 050003; 2. 陆军特种作战学院，广西 桂林 541000)

滚动轴承是机械设备的重要组成部件，是机械设备正常运行的保证[1]。滚动轴承振动信号中包含了丰富的运行状态信息，因此在滚动轴承故障诊断与状态监测过程中，发挥着重要作用[2]。但现场采集的振动信号通常受到较强的噪声干扰，故障信息往往淹没在强烈的背景噪声当中，难以提取反映滚动轴承运行的关键特征，使得振动信号的利用率极大降低，在很大程度上制约了滚动轴承效能的有效发挥。对于这一问题，振动信号降噪[3]是一种有效的解决方式。

小波分析[4]与形态学分析[5]是振动信号降噪中两种常用的方法。在不同应用条件下都取得了良好的降噪效果。

小波变换是目前运用最广泛的降噪方法。以小波分析理论为基础，文献[6]采用了双树复小波对信号进行分析，通过块阈值的方法，结合领域与空域，有效降低背景噪声。文献[7]对不同分解层次的系数求模，然后对系数采用非线性时间序列分析，消除随机噪声的干扰，最后再对系数采取软阈值去除直流信息，顺利提取轴承中的微弱故障成分，等等。分析小波降噪的原理，其充分利用了有用信号与噪声信号在小波域变换系数的特性，然后利用软阈值或者硬阈值的方式将部分小波系数滤除，从而保留下信号的有用信息。但是这种方式建立在信号整体特征的基础上提取有用信息，信号的降噪处理更多的是对信号进行一体化处理，因此在降噪过程中容易忽略每个采样点中所包含的细节信息，容易造成噪声信号与非噪声信号混杂，有时会抑制非噪声信号，严重影响了信号的降噪效果。

形态学分析是一种非线性分析工具，近年来在信号降噪领域得到广泛关注。以形态学分析为基础，文献[8]提出多尺度平均组合形态滤波方法，对原始振动信号进行降噪处理，实现对模态混叠的抑制。文献[9]研究了基于广义形态分量分析的降噪方法，首先把一维观测信号转换为多维虚拟观测信号，再借助广义形态分量分析方法，通过对观测信号的有效分离实现降噪。基于形态学分析的振动信号降噪方法主要利用腐蚀、膨胀、形态开运算、形态闭运算四种基本算子，并利用信号与结构元素的匹配相似度，实现有用信号与噪声信号的分离，达到降噪的目的。但是这种分析方式在信号处理过程中并没有充分考虑到信号的随机性对降噪效果的影响，并且对于某一特定振动信号而言，结构元素的选取对其信号处理过程的影响较大，导致结构元素的适应性弱，在一定程度上影响了形态学分析方法的降噪效果。

为进一步改进信号的降噪效果，本文改变传统的信号降噪理念，结合量子理论[10]，提出基于量子Hadamard变换[11]的降噪方法。该方法充分发掘量子理论在振动信号处理中的潜能，通过量子化的方法将振动信号单个采样点进行表达，赋予了单个采样点信号量子特性。通过量子化，单个采样点的幅值特性被弱化，而是转化成具有特定分布特性的概率分布模型。通过分析处理单个采样点的概率幅，判断信号是否为噪声信号，并对故障信号进行有效凸显。与基于小波变换的信号降噪方式相比，本文算法通过对单个采样点信号进行降噪处理，能够克服信号一体化处理带来的不足，避免了阈值处理过程中有用信号与噪声信号的混杂。与基于形态学分析的信号降噪方法相比，本文算法对单个采样点的降噪过程合理利用了采样点的概率分布特性，避免了降噪过程中信号随机性、结构元素等因素对信号降噪过程的影响，对分布参数的处理方法具有较强的适应性。实验结果表明，该方法能够有效改善信号的降噪效果，同时机械振动信号的故障特征得到凸显。

1 量子Hadamard变换

Hadamard变换(Hadamard Transform，HT)是量子理论框架下一种普遍使用的变换方式。HT与量子比特(Quantum Bit，QB)息息相关，在一个量子系统中，假设其QB长度为n，则该系统的态矢总数为N=2n。构造N×N的酉矩阵H(H=HT，HH=I)，将系统在二维空间下展开，那么HT通常可表示为[12-13]

(1)

量子比特表达式为

|Ψ>=a|0>+b|1>

(2)

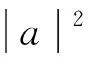
对量子比特|Ψ>=a|0>+b|1>应用HT可得

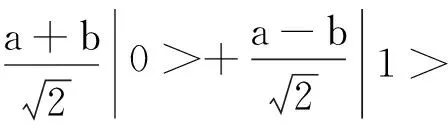
(3)

2 基于HT的振动信号量子化

2.1 基于HT的量子概率幅的参数范围

根据量子理论的相关约束条件，设定a，b∈[0, 1]，振动信号的状态包括噪声信号以及非噪声信号(故障信号)，为便于量子理论的应用，将故障信号设为基态|0>，将噪声信号设为基态|1>。对于实际采集的振动信号，其信号状态通常在故障信号以及噪声信号之间变化，故a，b可设定为

a,b∈(0, 1)

(4)

根据量子理论的基本知识，结合式(3)中可知，状态|0>出现的概率为

(5)

同理可得，状态|1>出现的概率为

(6)

式(5)和式(6)称为Hadamard量子概率(Hadamard Quantum Probability，HQP)。

从式(5)和式(6)中可以发现，对于不同的基本状态而言，其HQP取值取决于a×b，由于a，b为量子比特|Ψ>=a|0>+b|1>的概率幅，根据文献[14]，振动信号QB概率幅可以表示为

(7)

(8)

结合前文可知，p满足p∈(0,1)，故

(9)

对其进行一阶求导可得

(10)

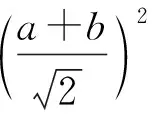
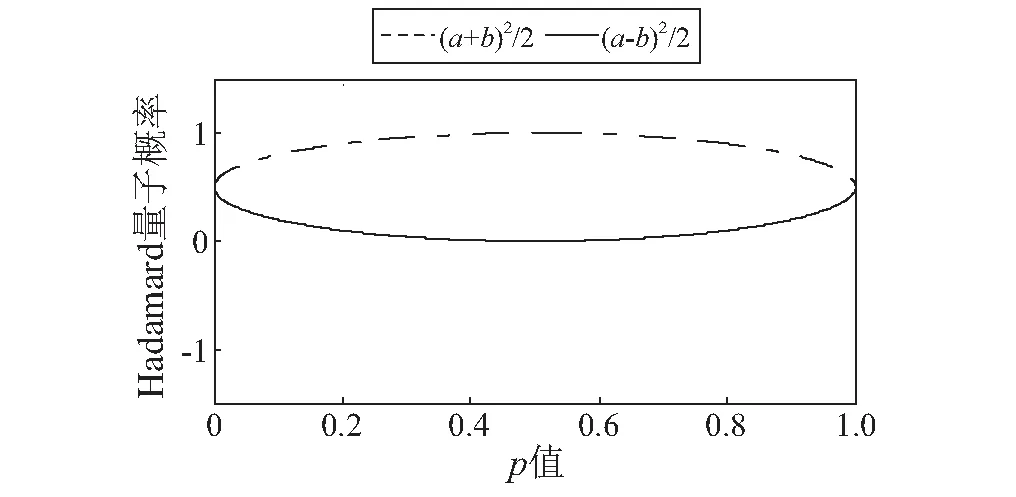
图1 HQP变化Fig.1 Change of HQP

为进一步简化过程，设定式(5)和式(6)在其可行域内单调增或者单调减，当p∈(0,0.5]时，a，b可以表示为

(11)

(12)

2.2 基于HT的振动信号量子化

结合前文可知，对于采集的振动信号，需要进行归一化处理

(13)

式中：s(k)为信号采样点，归一化处理后信号幅值z(k)∈[0,1]，量子化后的概率幅由z(k)折半生成，定义为

(14)

由于每一个信号点状态介于故障信号与噪声信号之间，对于QB，其概率幅可表示为

(15)

(16)

ε>0，为取值趋近于0的正值。进而进行量子化处理，可以表示为

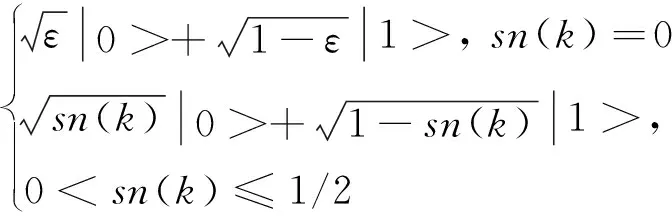
(17)

其中，

(18)

(19)

则根据陈彦龙等的研究，经过HT后，QB可以表示为

(20)

分析得知，经过HT后，式(5)、式(6)可表示为

(21)

(22)

从式中可以看出，基本状态|0>出现的概率与abs(s(k))呈正比，基本状态|1>出现的概率与abs(s(k)呈反比，因此采样点为故障信号的概率与abs(s(k))呈正比，为噪声信号的概率与abs(s(k)呈反比。

3 基于HT的降噪方法

3.1 可行性分析

3.1.1 衡量算子

对于滚动轴承的振动信号而言，若其不含有噪声，则信号间的关联性较强，而噪声信号会破坏这种关联性，因此本文借助量子理论提出衡量算子(Measurement Operator，MO)的概念。图2为振动信号1×3的邻近信号窗口。

sn(k-1)sn(k)sn(k+1)图2 1×3邻域位置关系Fig.2 1×3 neighborhood

衡量算子可以表达为

mo(k)=a(k-1)×a(k)×a(k+1)

(23)

式中：mo(k)为衡量算子；a(k)为振动信号量子化后的概率幅。

mo(k)可具体表达为

(24)

经过上述分析得知，mo(k)的大小不仅取决于k点sn(k)的大小，还取决于左右相邻点sn(k-1)，sn(k+1)的大小，因此在sn(k-1)，sn(k)，sn(k+1)均为较大值时，mo(k)才能取得较大值，结合振动信号的特点，通常故障信号在峰值附近sn能够连续取得较大值，因此故障信号在峰值附近取得较大值的概率较大。这种变化使得故障信号能够得到有效突出，有利于信号的降噪处理。

3.1.2 阈值确定

滚动轴承振动信号本身具有随机性，使得正向脉冲信号P和负向脉冲信号N的产生具有随机性，针对这种情况，可以从每一个采样点的自身特性出发，设定一个不同的阈值T(n)，并以阈值作为确定不同点处理方式的依据。

阈值的选取，对降噪效果有着至关重要的影响，当阈值选取过大时，可能会抑制信号中的非噪声信号，而当阈值较小时，噪声信号可能无法得到有效抑制，无法达到理想的降噪效果。考虑到脉冲信号P和负向脉冲信号N的随机性，本文提出与单个采样点信号特征相适应的阈值确定方式。

单个采样点阈值的确定通过中值滤波器(Median Filter，MF)实现，中值滤波器是一种平滑滤波器，在振动信号去噪中应用较多，通常情况下，无论是噪声还是故障信号都会导致振动信号发生突变，针对这一特点，本文设计合适的MF来选取合适的阈值，达到故障信号突出，噪声信号消除的目的，其过程可以表示为

T(k)=med(mo(sn(k-3)),,mo(sn(k+3)))

(25)

从式(25)中可以看出，采用MF滤波器，有效保证了阈值T(k)低于峰值点mo值。

3.2 降噪方法

3.2.1 正向故障脉冲信号处理

针对正向信号P，假设P在k点附近表现为故障，则故障特征越明显，a×b计算结果值越大，两种基本的状态在经过HT后概率变化情况为：式(5)取值变大，式(6)取值变小。根据分析得知，要达到故障突出表达的目的，对于mo(k)>T(k)的情况，该点信号应加强，对于mo(k)≤T(k)的情况，该点信号应减弱。因此可以利用式(5)、式(6)中的HQP实现信号降噪。在mo(k)>T(k)的条件下，该采样点很大概率上为故障信号，进而利用|0>的HQP增强信号

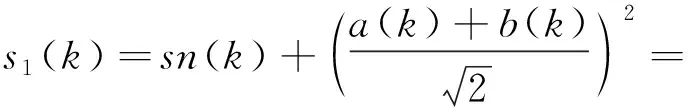
(26)

在mo(k)的HQP降噪

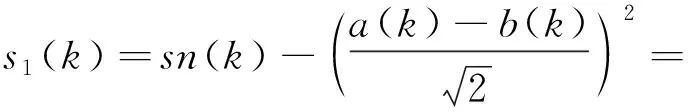
(27)

由式(26)、式(27)的计算结果可知，当mo(k)>T(k)时，信号加强的程度与信号幅值s(k)成正比；当mo(k)≤T(k)时，减弱程度与s(k)成反比。

由式(26)、式(27)分析得到

sn(k)+0.5≤0.5+sn(k)+a(k)×b(k)≤sn(k)+1

(28)

sn(k)-0.5≤-0.5+sn(k)+a(k)×b(k)≤sn(k)

(29)

从式(28)、式(29)中可以看出，对于不同采样点信号，若mo(k)>T(k)，sn(k)加强，加强的范围为0.5～1.0，且当sn(k)值较大时，sn(k)增加较多，最多增加1；若mo(k)≤T(k)，sn(k)数值减弱，减弱的范围为0～0.5，且当sn(k)值越小时，sn(k)减少的越多，最多减少0.5。

3.2.2 负向故障脉冲信号处理

针对负向信号N，假设N在k点附近表现为故障，在mo(k)>T(k)的条件下，该采样点很大概率上为故障信号，进而利用|0>的HQP进行负向增强

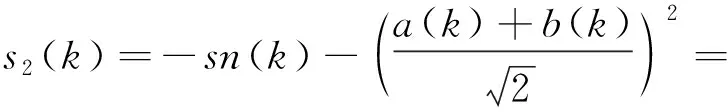
(30)

在mo(k)的HQP降噪

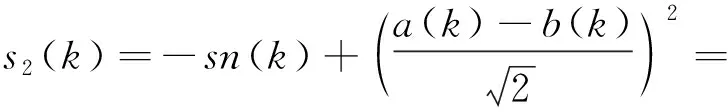
(31)

由式(30)、式(31)的计算结果可知，当mo(k)>T(k)时，信号减少的程度(故障信号加强)与信号绝对值成正比；当mo(k)≤T(k)时，信号幅值增加程度(故障信号减弱)与信号绝对值成反比。

由式(30)、式(31)可得

-sn(k)-1≤-0.5-sn(k)-a(k)×b(k)≤ -sn(k)-0.5

(32)

-sn(k)-0.5≤-0.5-sn(k)+a(k)×b(k)≤ -sn(k)

(33)

从式(32)、式(33)中可以看出，对于不同采样点信号，若mo(k)>T(k)，-sn(k)数值得到减少，减少的范围为0.5～1.0，且当-sn(k)值较小时，-sn(k)减少较多，最多减少1；若mo(k)≤T(k)，-sn(k)数值增加，增加的范围为0～0.5，且当sn(k)值越大时，-sn(k)增加的越多，最多增加0.5。

4 降噪算法步骤

根据上述分析，通过HT得到了滚动轴承振动信号时域处理算法，该算法对振动信号进行量子化处理，进而实现噪声的消除与故障信号的增强，并且在整个过程中参数变化具有适应性。基于量子HT的分析方法(Analysis Method Based on Quantum Hadamard Transform，AMQHT)步骤可以描述为：

步骤1基于HT，利用式(13)、式(14)实现振动信号的量子化，处理方法如式(20)所示；

步骤2利用HT，对每一个信号点进行处理，根据式(21)和式(22)计算出不同点对应的HQP；

步骤3利用式(23)，计算不同信号点的MO值；

步骤4利用式(25)确定不同信号点的T(k)大小；

步骤5若采样点满足s(k)≥0，设定为P(正向)，利用式(26)和式(27)进行降噪处理。

步骤6若采样点满足s(k)<0，设定为N(负向)利用式(30)和式(31)进行降噪处理。

另一个方面，上述步骤5、步骤6，根据分析可以看出，出现在s(k)≥0区域的波谷，处理完之后同样为波谷；出现在s(k)≤0区域的波峰，处理完之后同样为波峰。因此，经过本文算法进行处理后，波峰波谷区域在实质上并不会改变。

5 实验结果与分析

5.1 仿真信号实验

为验证本文算法的有效性，设计仿真信号，进行信号的降噪实验。

仿真信号采样频率为960 Hz，采样时间为1 s。仿真信号中成分主要包括两部分

y=y1+y2

(34)

式中：y为仿真信号；y1为本底信号，其表达式为

y1(t)=sin(2π×100×t)+sin(2π×200×t)

(35)

y2仿真噪声信号，实验中，为分析不同类噪声对本文算法降噪效果的影响，分别设置了不同种噪声信号，包括白噪声、有色噪声、脉冲干扰。在滚动轴承振动信号采集过程中，真实信号通常会淹没在背景噪声之中，因此设置白噪声、有色噪声标准差为4，有色噪声表达式可以表示为

e(k)=x(k)+0.5×x(k-1)

(36)

式中：x(k)为白噪声信号的第k个点。脉冲干扰为周期性的冲击信号，单个脉冲信号可以表示为

p(t)=A0e-40×t·cos(2π×150×t)

(37)

式中：A0为幅值，仿真实验中设置A0=4，载波信号的频率为150 Hz，冲击频率为10 Hz。仿真信号时域如图3所示(图中时间为0.5 s)，频谱如图4所示。从时域图中可以看出，本底信号完全淹没在噪声信号中，而在频域内，本底信号特征频率也受到严重污染。

图3 仿真信号时域图Fig.3 The simulated signals in time domain

图4 仿真信号频域图Fig.4 The simulated signals in frequency domain

针对上述仿真信号，利用本文所提的AMQHT算法进行降噪，降噪信号的频谱如图5所示，从图中可以看出，对于白噪声和有色噪声，经过AMQHT降噪后，本底信号的特征频率得到了充分保留，同时噪声信号在频域内受到了有效抑制，这就使得频域内特征频率得到了有效凸显。实验结果表明，当原始信号淹没在白噪声、有色噪声信号中时，本文算法能够降低噪声的干扰，实现有用信号的凸显。而对于脉冲干扰而言，本文算法很难将其与本底信号相区分，甚至将脉冲干扰当做有用信号进行凸显，因此在图5(d)中，本底信号、脉冲载波信号、脉冲频率均得到保留。实验结果表明，本文算法对脉冲干扰的抑制效果不足。

图5 降噪效果Fig.5 The de-noising effect

5.2 实测信号实验

为进一步验证本文算法的有效性，利用实测信号进行降噪实验。故障信号来自于某型滚动轴承变速箱。在变速箱的轴承上设置内圈故障。在轴承内圈上加工出1 mm×0.2 mm(长×深)的划痕。采集加速度振动信号，实测转动速度1 748 r/min(29.1 Hz)，传感器安装在对应轴承位置的箱盖上方。

滚动轴承内圈故障的特征频率计算公式为

(38)

式中：n为轴承转速，r/min； 转频fr与转速n的关系为fr=n/60；D为轴承中滚动体的直径；D为轴承的节径；β为轴承的接触角；z为滚动体的个数，经过计算，内圈故障理论频率应为f=157.7 Hz。

振动信号的采样频率fs为12 kHz，采样时间0.6 s，图6显示了变速箱轴承内圈发生故障时的振动信号时域波形及其频谱。时域波形中虽然出现了冲击的信号，但是振动信号的频谱却难以观测到故障特征频率f。

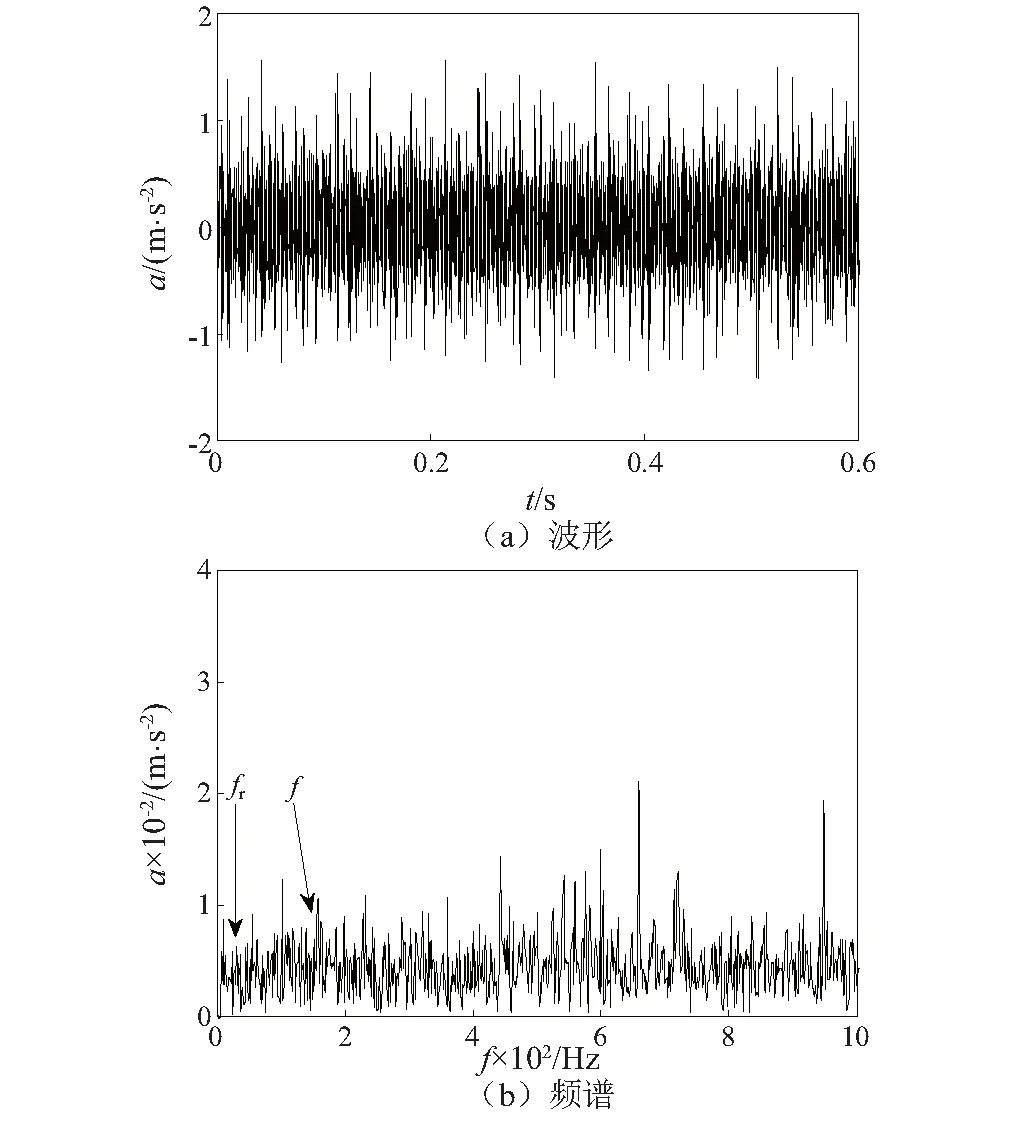
图6 滚动轴承内圈故障的振动信号Fig.6 Vibration signals from rolling bearing with fault in inner ring

为验证本文所提算法的效果，利用轴承内圈故障信号进行降噪实验，降噪效果如图7所示。

对降噪后的轴承内圈故障信号进行傅里叶变换，频域特点如图7(b)所示。从图中可以看出，利用AMQHT降噪后，故障信号频率f和及其二倍频2f得到有效表示。

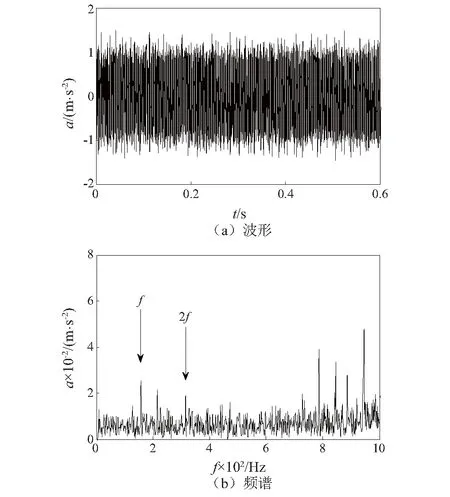
图7 AMQHT处理结果Fig.7 Result of AMQHT

为进一步验证本文算法的降噪效果，利用不同算法对上述内圈故障信号进行降噪处理，对比不同算法的降噪效果，对比的算法为数学形态学(Analysis Method Based on Mathematical Morphology，AMMM)。降噪后时域波形与频谱，如图8所示。

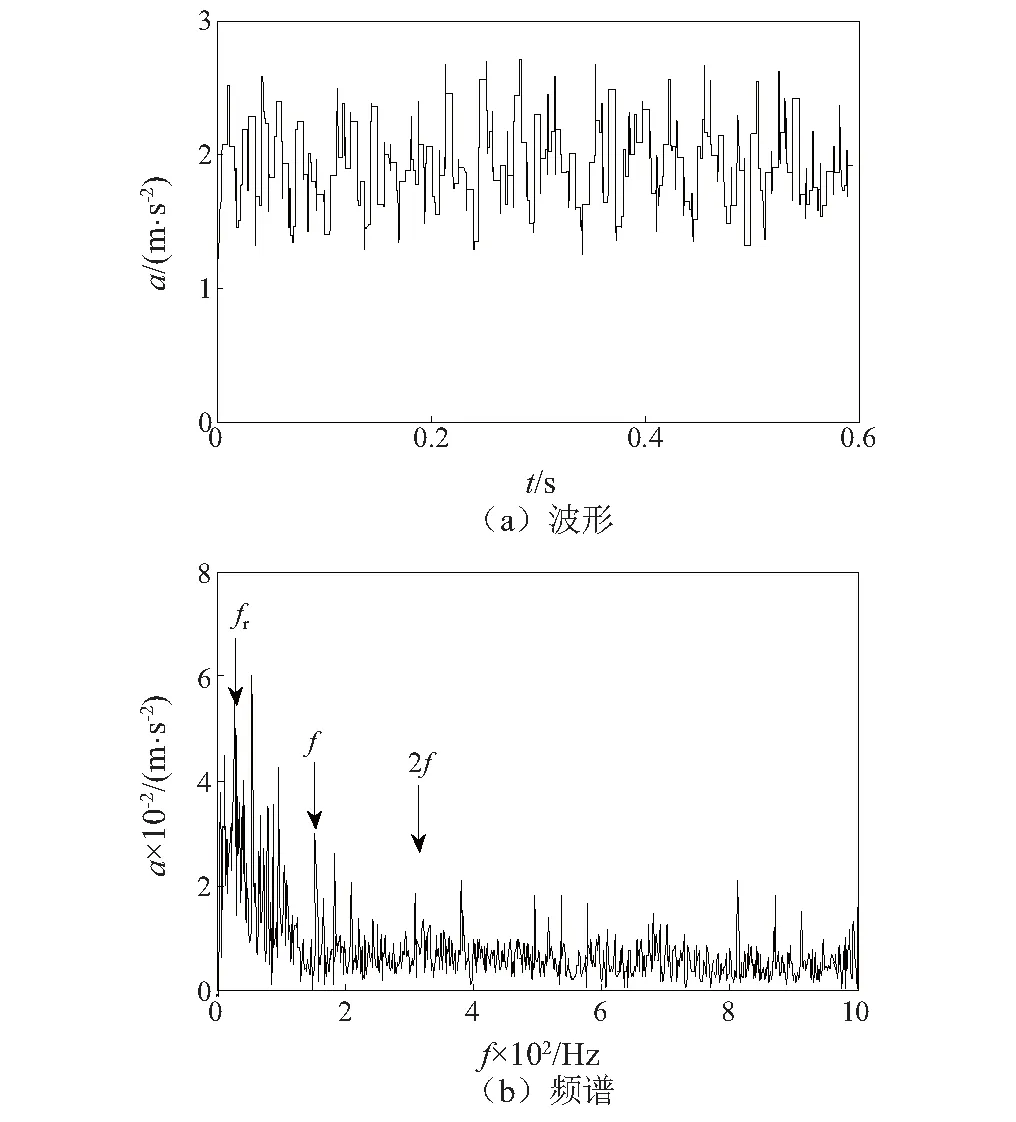
图8 AMMM处理结果Fig.8 Result of AMMM

为量化降噪算法的降噪效果，引入三个振动信号降噪的量化指标

(1) 降噪指标

(39)

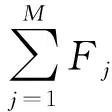
(2) 增强指标

(40)

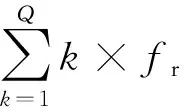
(3) 频率指标

频率指标表示故障特征频率f的幅度。

不同算法的降噪效果如表1所示，可以看出，在频率指标上，AMQHT稍差于AMMM，但从降噪指标及增强指标来看，AMQHT要好于AMMM。分析其原因，AMMM对故障信号的增强效果要稍好于AMQHT，但由于AMMM对信号进行处理过程中，很难实现故障信号与非故障信号的有效分离，因此容易将非故障信号进行增强，表现在降噪指标与增强指标上，AMMM要差于AMQHT。综合分析，AMQHT降噪效果要好于AMMM，实验结果充分验证本文算法的有效性。

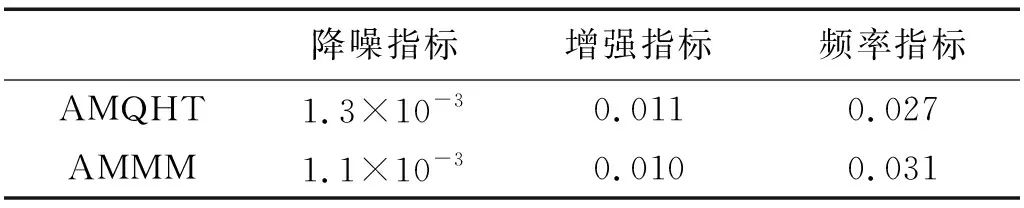
表1 降噪效果对比Tab.1 Comparison of de-noising effect

6 结 论

针对滚动轴承信号的降噪问题，引入量子Hadamard变换，建立起一种用于滚动轴承故障状态下的振动信号分析方法。该方法以量子理论为基础，深入考虑每一个采样点中噪声和故障信息的变化。将每一个采样点进行量子化后，独立分析每一个采样点的信息，有效克服了现有降噪算法对细节信息考虑不充分的问题。最后，将本算法应用于实测轴承内圈故障振动信号的降噪，验证了本文算法的有效性。