基于扰动观测器的电液比例系统滑模位置控制*
韩光耀, 施光林, 郭秦阳
(上海交通大学 机械与动力工程学院,上海 200240)
0 引言
电液控制系统(包括电液力/位置/速度控制系统)由于具有功率密度大、刚度高、响应速度快以及传递运动平稳等优点,广泛应用于冶金机械、化工机械、机床、加载试验机以及机器人等领域[1]。对于电液比例阀控缸系统,一般的方法是根据电液比例阀和液压缸的动态方程建立电液系统的数学模型[2],然后基于数学模型设计控制器。然而,在建立数学模型的过程中,往往会忽略一些对控制策略设计非常重要的因素或者无法对其精确的建立模型,比如系统运动过程中受到扰动力、液压油参数随温度的变化、泄漏、摩擦参数的不确定性、参数的非线性等[3-5]。对于一些加工机床而言,执行机构在运动过程中由于末端执行器(比如刀具、压头等)受到被加工件的干扰(比如随主轴转动的工件存在振动等)导致系统负载存在扰动[6]。特别的,对于一些并联机构而言,因为支链间互相耦合,每个支链对的驱动缸都受到较大的扰动。上述问题依靠电液系统自身的鲁棒性能难以克服,使得难以实现精确的控制。
在过去,对于电液控制系统广泛采用在工作点附近将非线性动态进行线性化从而利用线性控制理论[7-8]。然而传统的线性控制并不能保证电液系统的鲁棒性和控制精度。为提高电液控制系统的控制效果,一些先进的控制算法被提出。文献[9]提出一种模糊PID的控制策略以适应位置控制过程中的非线性及负载扰动。文献[10]提出一种自适应鲁棒控制器用于受到未知恒定负载的电液位置控制系统。上述通过增强系统的鲁棒性以适应系统的非线性和负载扰动的方法,通过实验和仿真证明可在一定程度上提高系统的控制精度。但是,当负载存在较大扰动时,难以实现较高的控制精度。滑模控制器本身具有很强的鲁棒性,设计滑模控制器时只需其负载扰动有界,但若可以更近一步在线估计出非线性扰动的大小,将会大幅提高系统的控制精度。故本文设计了一种基于扰动观测器的滑模控制器,此控制器通过扰动观测器估计难以建模的未知干扰力,实现对干扰的模型补偿。同时,滑模控制器以应对电液控制系统的非线性、模型偏差等。最后,算法进行了仿真验证。
1 系统描述与模型建立
一个带负载扰动的电液比例阀控缸驱动的并联机构如图1所示。该系统用于并联机构加载试验台中,利用液压缸驱动并联机构的支链,实现并联机构末端执行器沿预定加载轨迹移动。末端执行器在加载移动过程中,被试件会随主轴一同旋转,此时,阀控缸驱动的并联机构会产生明显的非线性外负载扰动,导致电液系统的位置跟踪过程中出现抖动、跟踪精度差等现象。
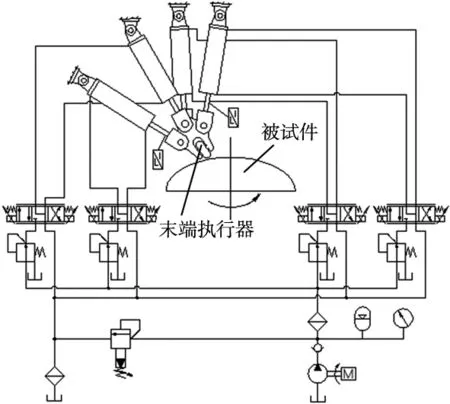
图1 并联机构电液系统原理图
由于篇幅限制且不是本文讨论的重点,并联机构的运动学和动力学的正逆求解过程本文不做叙述。特别指出,反解出的负载为理论负载,扰动观测器用于观测液压缸受到的扰动干扰负载、因加工安装误差产生的理论负载的计算误差和液压缸运动受到的摩擦力。
1.1 电液比例阀模型
电液比例阀是电液位置控制系统的核心控制元件,对于本研究所采用的零遮盖四通滑阀,其阀口输出流量方程如式(1)所示:
(1)
式中,
其中,P1,P2—分别为有杆腔和无杆腔压力;Ps,Pt—分别为油源和回油压力;u—电液比例方向阀的输入信号;Cd—阀口的流量系数;ku—为电液比例方向阀增益,xv=kuu;ρ—液压油密度;w—节流阀口面积梯度。
1.2 液压缸动态模型
对于单出杆双作用液压缸,其无杆腔和有杆腔的流量连续性方程如式(2)和式(3)所示:
(2)
式中,xp—液压缸活塞杆位移;A1—液压缸无杆腔有效面积;Ci—液压缸内泄漏系数;V1—液压缸无杆腔有效容积,V1=V01+A1xp,其中V01为液压缸无杆腔初始容积,包括连接管道内容积。
(3)
式中,A2—液压缸有杆腔有效面积;
V2—液压缸有杆腔有效容积,V2=V02-A2xp,其中V02为液压缸有杆腔初始容积,包括连接管道内容积;
Ce1、Ce2—分别为液压缸无杆腔、有杆腔外泄漏系数。
液压缸活塞杆的动力学平衡方程为:
(4)
式中,m—液压缸活塞杆的总体等效质量;Fl—液压缸活塞杆上受到的理论负载;d—扰动干扰负载、因加工安装误差产生的理论负载的计算误差和液压缸运动受到的摩擦力。
1.3 电液比例位置控制系统状态空间模型
定义状态变量:
(5)
则根据式(5)可知:
(6)
由式(4)可以得到:
(7)
结合式(2)和式(3)可以得到状态变量x3、x4的状态方程:
(8)
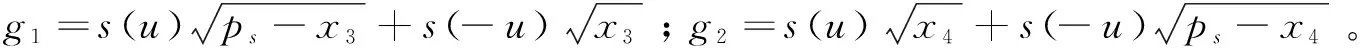
综合式(6)、式(7)和式(8)得到电液比例位置控制系统的状态空间表达式为:
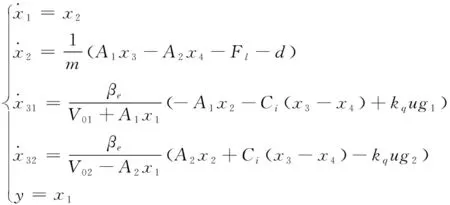
(9)
2 控制器的设计
2.1 扰动观测器的设计
本节设计扰动观测器用来估计式(9)中扰动d的值。式(9)可以被写成:
(10)
在设计控制器之前,先做出以下合理假设:
假设1:扰动d有界,且其微分亦有界[11],即
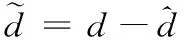
(11)
扰动估计的微分为:
(12)
其中l0为观测增益,正值。
设计扰动观测器[12]为:
(13)
ξ·=-l0(ξ+l0mx2)+l0(A1x3-A2x4-Fl)
(14)
式中:ξ为辅助变量。
选定一个半正定的Lyapunov函数:
(15)
V0对时间求导[13]为:
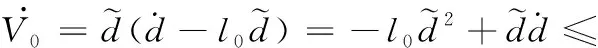
(16)
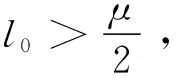
2.2 滑模控制器的设计
首先定义系统的误差变量:
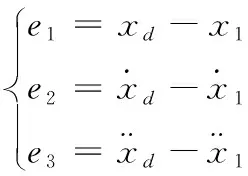
(17)
设计滑模的切换函数为:
s=c1e1+c2e2+e3
(18)
选择指数趋近律为:
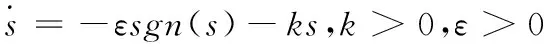
(19)
则:
(20)
根据式(9),可得:
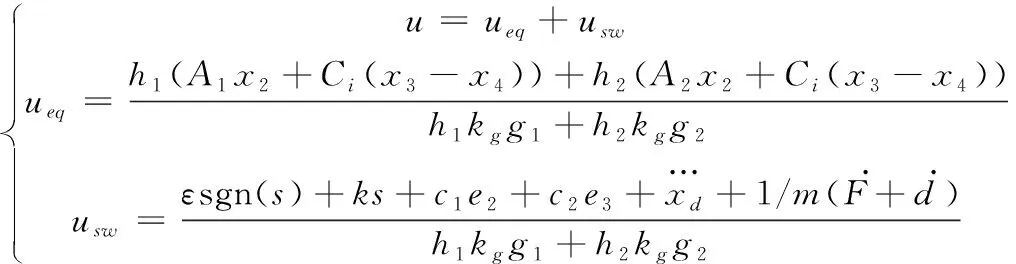
(21)
式中,
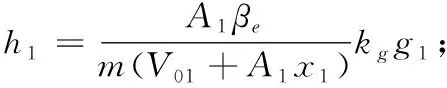
值得注意的是,变量g1,g2中含有变量u,即控制器的计算输出u与u的正负值有关,显然存在一个代数环。但幸运的是,式(21)中u表达式的分母项恒为正值,故可用u的分子项正负来替代u的正负。
3 仿真实验与分析
本节利用MATLAB/Simulink对上节所提出的基于扰动观测器的滑模控制系统进行仿真验证。电液比例系统的数学模型如式(9)中状态空间表达式所示,式(21)为所设计的滑模控制器。完整的电液比例控制系统的原理框图如图2所示。其中,液压系统的基本参数如表1所示。
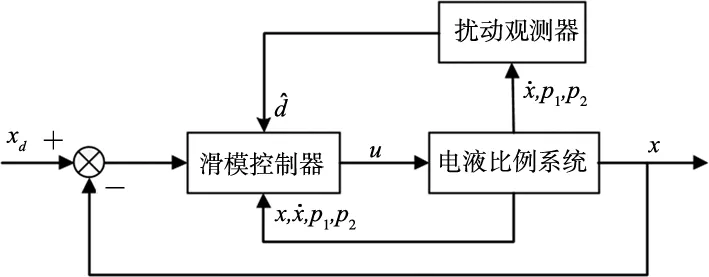
图2 电液比例系统控制方框图

参数值A13.117×10-3m2A21.527×10-3m2V010.92×10-3m2V021.8×10-3m2m40kgβe2000barPs21×106Pakq1.019×10-7
仿真中控制器设置的参数值见表2。

表2 SALBP方案2优化结果
在本并联机构的单液压缸控制的过程中,理应用到并联机构反解出的特定理想轨迹和理论负载曲线,然而,为了验证所设计的控制器的一般性,在仿真过程中均采用正弦曲线。设定期望位移曲线为xd=0.4sin(0.6πt)+0.4,反解出的理论负载假定为Fl=20000sin(0.4πt),将非线性外负载扰动力设定为d=50000sin(0.8πt)。
图3给出了无扰动观测器的传统滑模控制器在负载干扰下对给定曲线进行跟踪的结果,从中可以看出仅采用滑模控制器的控制误差在±1mm左右。
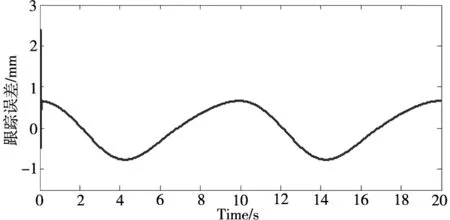
(b)位置跟踪误差图3 传统滑模控制器
图4 给出了所设计的非线性扰动观测器对电液系统存在的负载扰动的观测结果,其中,da为扰动观测器实际扰动估计值,dD为仿真中施加的负载干扰。从图中可以看出该观测器可准确估计出在仿真中给系统施加的负载干扰,从而可有效地对系统进行干扰补偿。

图4 扰动负载与估计曲线
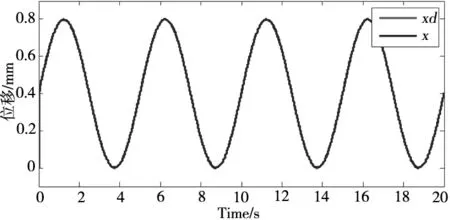
(a)位置跟踪曲线
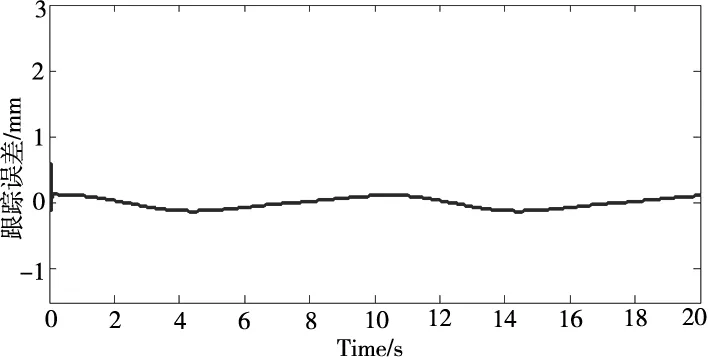
(b)位置跟踪误差图5 基于扰动观测器的滑模控制器
图5给出了基于负载扰动观测器的滑模控制器的跟踪效果。从图中可以看出其控制精度可达到±0.2mm,与无观测器的滑模控制相比,其控制精度得到显著提高。采用扰动观测器对系统中的未知非线性负载及非线性进行估计与补偿的方法可大幅度提高位置控制的精度。
4 结论
根据电液比例系统数学模型,设计一种可估计未知干扰负载的扰动观测器,并证明了其稳定性,并将其与滑模控制器相结合设计出了电液比例系统的非线性滑模控制器。通过仿真结果表明,所设计的扰动观测器可以准确估计未知负载干扰,使存在未知非线性扰动的系统具有很好的鲁棒性,从而达到更高的跟踪精度。总之,基于扰动观测器的滑模控制器可对存在非线性扰动的电液比例位置系统实现更好的控制效果。

