光伏储能系统的电池容量配置及经济性分析
倪驰昊,刘学智
(上海交通大学 电子信息与电气工程学院,上海 200240)
0 引言
能源是国民经济的重要物质基础,是经济发展的源动力,也是决定生活质量的重要因素。随着能源需求的日渐增长,很多国家在可再生能源的开发和利用上进行了探索和实践。我国的生活电力消费量逐年增加,这要求电力生产量提高的同时要提高能源转换效率,并重视发展新能源发电技术,增加清洁能源发电比重。
光伏发电具有清洁、无污染、技术成熟等优点,其中一种收益方式来源于3个方面:自用节省的电费、国家及部分地方补贴、出售给电网的电费收入[1]。电池储能技术能将光伏发电过剩电量储存起来,也可以从电网中获取和存储电能,能够辅助满足系统的电负荷,也能有效提高系统对间歇性可再生能源的接纳能力。不加装储能装置的光伏并网发电系统会对电网造成不良影响[2],将储能系统光伏发电结合统筹规划,能够增强系统的可协调性和灵活性,为用户带来最大化的收益。光伏与电池储能耦合的收益来自于2个方面:存储多余光伏电力时的电网电价与光伏外送电价之差;存储多余光伏电力时的电网电价与释放这部分电力时的电网电价之差。
当前国内外对光伏储能系统的研究中,运用了多种方法建立系统的经济模型,并对有无储能电池的光伏发电系统的经济效益进行了评估对比[3],计算了储能电池的经济效益。在现有光伏发电设备的基础上,合理配置电池容量和功率是光伏储能系统规划的关键[2-7]。容量太小无法有效地消纳光伏电力,容量太大则电池的投资成本太高,所以在电池的容量与价格之间有一个最优平衡点。目前国内外对于光伏-储能系统配置运行调度有大量研究,侧重于个体用户以住宅或楼房为单位,从个体角度讨论收益最大化问题[9-19]。目前国内外对区域光伏储能系统同时进行容量配置与运行策略优化的研究较为有限。另外,由于国家政策、区域气候资源对光伏和负荷的影响,国外的研究结论不能复制到国内。目前多使用的方法是根据负荷和光伏日发电预测曲线和分时电价特性[2],对光伏储能系统建立系统模型[9],将加入储能成本后的综合费用作为目标函数,通过对目标函数的优化来确定储能电池的配置方案[6]。本文在此基础上运用月平均数据法将负荷、光伏的全年数据输入优化程序,提高了数据的代表性;根据优化目标函数与约束条件对电池充放电策略进行优化,提高了模型的适用性。
本文基于实际的工业园区示范项目,通过具体案例的电池储能规划,求解线性规划模型,将电池容量、功率及系统全年电池充放电功率、购电售电功率等参数进行统一优化计算,得到最优化的电池充放电策略及电池容量和功率配置结果的方法。首先,将系统全年8 760 h负荷、光伏出力、分时电价等数据转化为288 h月平均数据;然后选取将电池容量、功率和288 h下的系统全年电池充放电功率、购电售电功率等作为优化参数,列出优化参数的约束条件,及月平均数据表示下的目标函数即系统全年费用支出;最后,将负荷、光伏出力、电价及电池相关参数等数据代入优化函数进行计算,得出最佳的电池配置方案。分析了光伏上网价格、储能电池成本、电池寿命和折现率等因素变化对电池储能容量配置和经济效益的变化规律。
本方法适用于各种不同的采用分时电价的光伏储能系统,保证了求得的电池配置结果是在最优化的充放电策略下得出的,系统的各部分功率作为输出结果,便于进一步分析储能和光伏的耦合及其在系统中发挥的作用。可以根据光伏储能系统的具体要求及不同储能电池的特性,对目标函数进行修改和对约束条件进行增删,具备可拓展性。同时,可以通过修改优化程序中的各参数数值,从而得到各个参数变化对储能配置结果和电池充放电策略的影响。
以广东某工业园区的光伏储能系统为例,利用文中方法编写能求出使经济效益最大化的储能容量和功率配置结果的优化程序,并在储能电池投资成本及光伏补贴和上网电价逐年降低的背景下,分析储能电池在系统中所发挥的作用。
1 系统建模和案例分析
本节主要内容包括案例概述和系统模型的构建2个部分:在案例概述部分将主要介绍案例中光伏储能系统的概况,负荷、光伏及电价数据等信息;系统模型部分将主要介绍加装储能电池的光伏系统的能量流动方向及电池的充放电功率约束和电池电量约束,选取优化参数并计算考虑电池成本情况下的目标函数。以此为基础进行园区加装电池储能设备的容量和功率优化配置及经济效益等问题的研究。
1.1 案例概述
本文所使用的案例为广东从化工业园区的光伏储能系统,园区光伏出力可用于满足负荷或出售给电网,增加储能设备后,光伏发电可为储能电池充电。
园区光伏发电的自我消纳能力用参数指标SCR(自我消纳率)来衡量,其定义为:

式中:PPV.dmd为光伏提供给负荷的功率;PPV.charge为光伏为电池充电的功率;PPV为光伏出力。
根据式(1)可计算系统全年光伏产生电能的自我消纳率。SCR的值越高,说明系统对光伏发电的消纳能力越强。
储能电池带来的经济效益可以用IRR(内部收益率)来衡量。IRR是资金流入现值总额与资金流出现值总额相等、净现值等于零时的折现率,数值越高,系统的经济效益越好。对于储能电池而言,IRR的计算主要考虑电池投资成本和每年储能电池带来的收益两部分,可在优化程序中计算IRR的具体数值。
本文数据基于一个工业园区示范项目[1],包括园区的年低方案负荷预测、CHP(热电联产)出力、电价、光伏出力预测8 760 h数据。园区电负荷为根据园区各企业和行业的相关数据,使用年最大负荷利用小时数法计算得出的园区2020年低方案负荷预测数据。园区的CHP已经投产,且年供热量和发电量数据已知,CHP发电的出力优先用于满足负荷。本文主要关注的是光伏储能系统的经济效益,因此可将园区负荷功率减去CHP发电功率(小于零的数值以零处理),将其看作等效负荷,为方便讨论,计算中所使用的负荷数据为等效负荷,其全年数据如图1所示。
图2为根据当地典型年气象参数以及园区光伏设备的相关参数计算得出的园区2020年光伏发电功率8 760 h预测数据,光伏出力呈现较明显的周期性变化,在白天光伏发电功率较高,夜间出力基本为0,全年光伏出力峰值为26 MW。
园区光伏设备已经建成,在经济效益计算时不考虑光伏设备的投资成本。光伏发电可提供给负荷及储能电池充电,或出售给电网,当地光伏上网电价Csell=0.451 5元/kWh,同时,园区光伏发电每度电可获得补贴Csub=0.42元/kWh。
但随着政策的变化,光伏补贴和上网电价都呈现出逐年降低的趋势。显然,光伏度电补贴的减少会降低园区光伏储能系统的经济效益,但补贴金额由全年光伏发电量决定,不会因储能的引入而产生变化。而上网电价的降低将可能会在一定程度上影响电池的充放电策略,因此上网电价不一定选用上述具体数值,这会在后文进行讨论分析。
该工业园区采用分时电价,每日0:00-8:00(L时段)从电网购电电价Ce=0.352 2元/kWh,每日 8:00-14:00(M1 时段)、17:00-19:00(M2 时段)、22:00-24:00(M3 时段)购电电价 Ce=0.655 5 元/kWh,每日 14:00-17:00(H1 时段)、 19:00-22:00(H2 时段)购电电价Ce=1.049 9元/kWh,如图3所示。
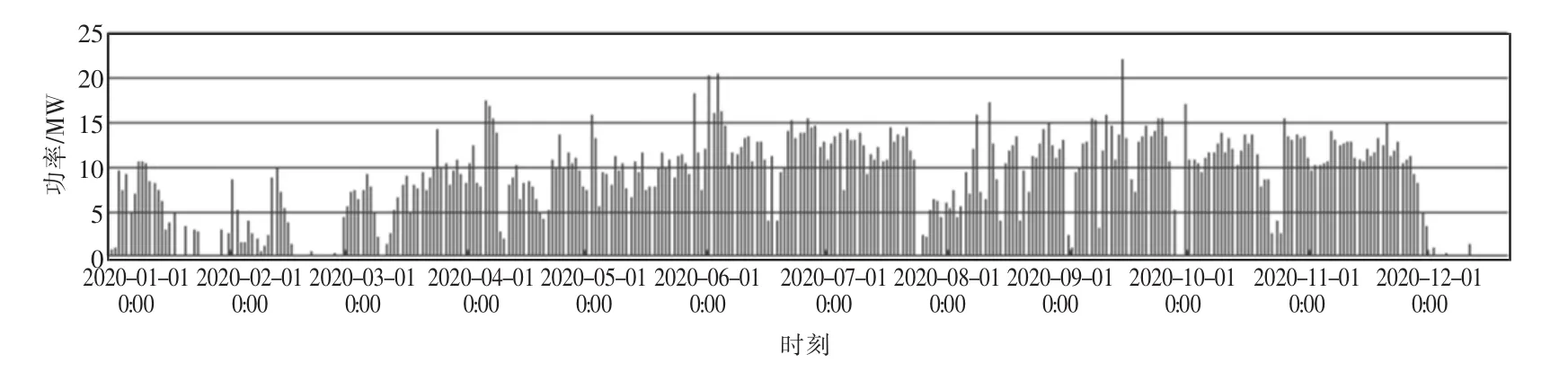
图1 园区2020年等效负荷预测数据
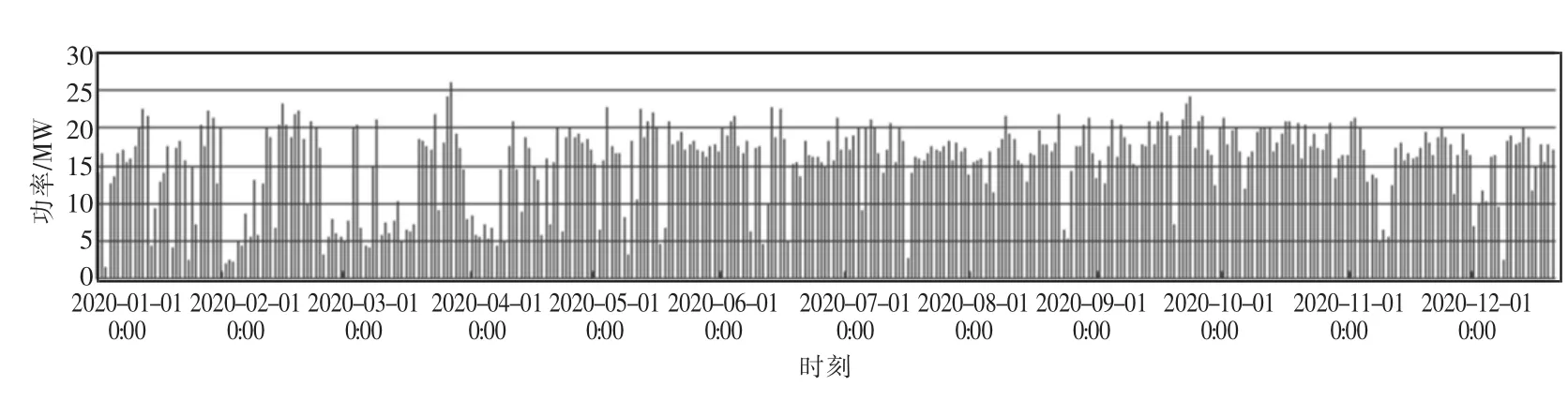
图2 园区2020年光伏出力预测数据
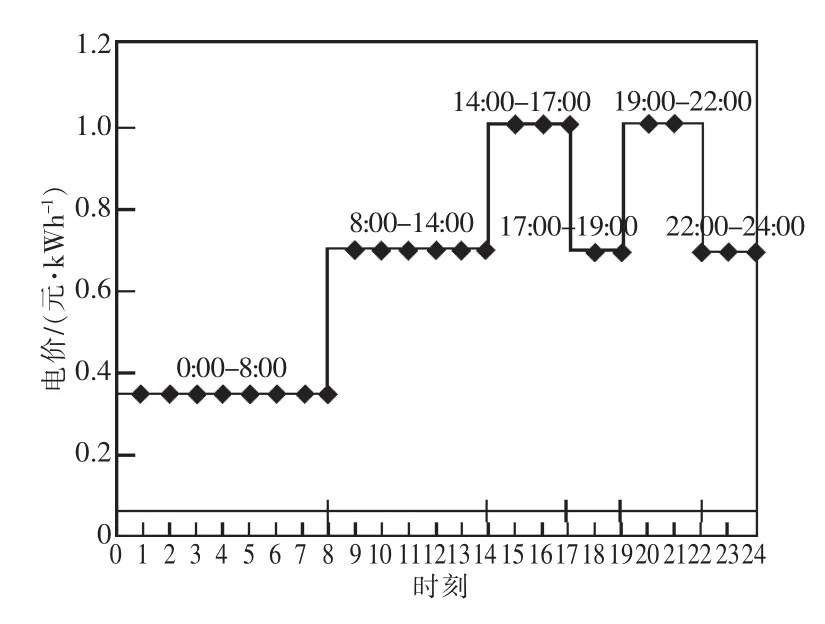
图3 广东省10 k V大工业峰谷电价曲线
本算例选取深圳欣旺达公司的锂电池储能产品,所涉及到的部分参数如表1所示[8]。
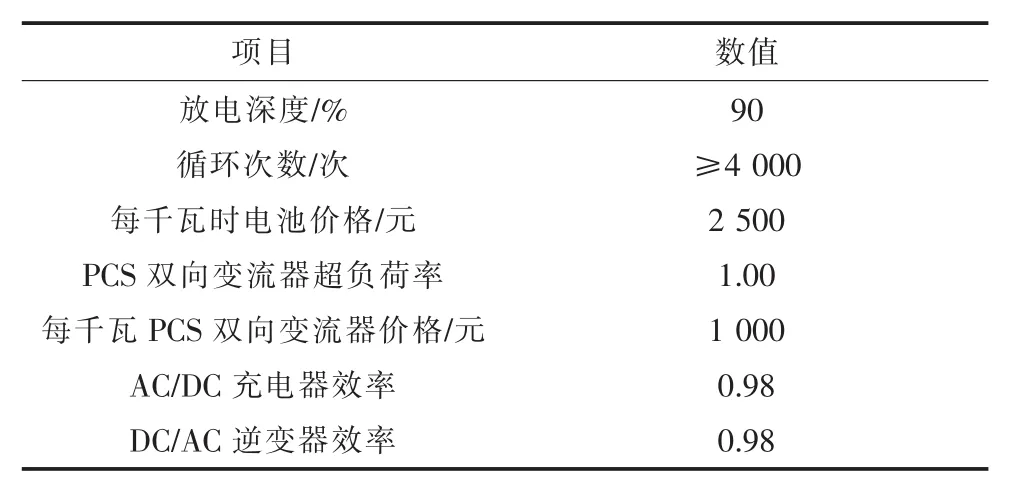
表1 储能电池相关数据
1.2 系统模型
园区在现有光伏发电的基础上,加装储能电池设备,投资规划的关键是确定最优的电池容量和功率配置方案。由于峰谷电价的影响,利用电池储能系统,在满足园区负荷需求的情况下进行峰谷差价套利,可以有效带来经济效益。本文利用Matlab软件的fmincon函数,介绍了一个能够根据负荷、光伏出力及电价数据,对系统各部分间的功率流动进行合理分配,得到最优情况下电池所需配置的容量及功率,并具备普遍性和可拓展性的优化程序。
1.2.1 优化参数选取和数据处理
储能电池的容量Smax和最大充放电功率作为主要优化配置的对象。系统中光伏设备、储能电池、电网及负荷之间的各部分功率也需要纳入优化参数中。该园区光伏储能系统的功率流向如图4所示。
图4显示了光伏出力、电网购电功率、电池充电功率的流向和组成,这6组功率合理分配是系统收益最大化的核心。若选取其中4组作为优化参数,包括288 h中每小时中光伏提供给负荷功率 PPV.dmd(t), 光伏给电池充电功率 PPV.charge(t),从电网购电给电池充电功率Pbuy.charge(t),电池放电功率Pdischarge(t),则剩余2组功率可以由前4组表示出来。
现有数据为园区全年8 760 h低方案负荷、CHP出力、光伏出力、电价数据,为每小时记录1次。将全年8 760 h里每小时的各部分功率作为优化参数是不现实的,可通过求出1个月内每天对应小时各功率数据的平均值即24 h月平均数据,作为典型日数据来代替该月光伏出力、负荷功率等数据,全年总计需要288 h的相关数值。
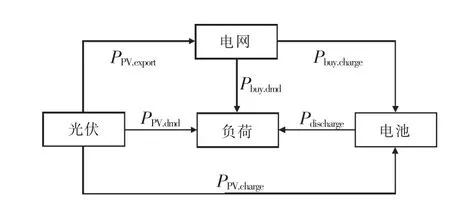
图4 系统功率流向
在全年288 h平均数据中,第t小时的PPV.dmd(t),PPV.charge(t),Pbuy.charge(t),Pdischarge(t)分别表示为fmincon 函数中的参数 x(t), x(2t), x(3t), x(4t),加上电池容量Smax和电池最大额定充放电功率表示为 x(1153)和 x(1154), 后文中所述的约束条件将围绕这参数展开。
1.2.2 模型约束和目标函数
对于园区的光伏储能系统,系统模型中各参数的约束条件主要分为电池充放电功率约束和电量约束,在fmincon优化函数中分为线性不等式约束、线性等式约束、非线性不等式约束、非线性等式约束以及优化参数初值、上下界等部分。
1.2.2.1 电池充放电功率约束
由图4可以得出园区光伏出力、从电网购电功率和园区负荷与图中各功率流的组成关系。
园区每时刻的光伏出力PPV(t)分为提供给负荷功率 PPV.dmd(t), 给电池充电 PPV.charge(t), 售给电网 PPV.export(t)等 3 个部分, 即:

从电网购电功率Pbuy(t)分为用于满足负荷功率 Pbuy.dmd(t)和给电池充电功率 Pbuy.charge(t):

每个时刻园区的负荷由光伏、电网购电和电池放电3部分满足,即:
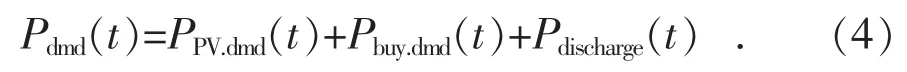
根据式(2)—(4),可以得出各优化参数的约束不等式:

其中:式(6)和(7)为优化参数的线性不等式约束;由式(5)可以得到fmincon函数中参数PPV.dmd(t)的下界为 0,上界为 Pdmd(t)。
根据光伏储能系统的结构和运行特征,还可进一步确定电池充放电功率的其它约束。由于每个时刻电池的充放电功率在额定范围内,不超过额定最大充放电功率有以下各式:
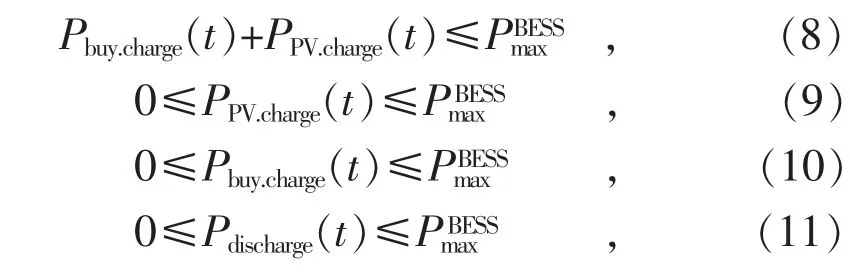
其中: 式(8)为线性不等式约束; 式(9)—(11)确定了 fmincon 函数中参数 PPV.charge(t), Pbuy.charge(t)和Pdischarge(t)的下界为 0, 上界为。
由于储能电池的充放电不会同时进行,则有:
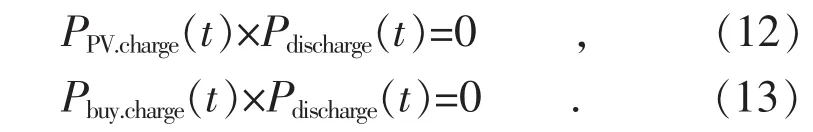
由式(12)和(13)可求得 fmincon 函数中的非线性不等式约束。在优化程序中,非线性约束会显著增加运算量,因此该约束的存在会严重影响运行效率,在后文中会介绍该约束条件可以去除的理由。
储能电池的引入不应增加系统从电网购电功率即Pbuy(t)的峰值,从而给系统造成额外的负担,若未使用储能电池时全年购电功率峰值为则有:
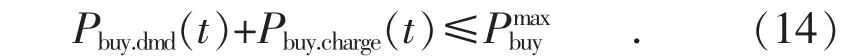
将式(4)代入式(14),可得到:
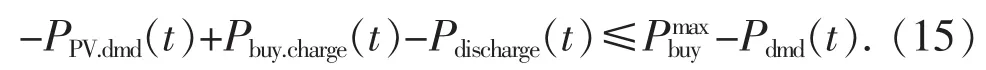
式(15)即为相应优化参数的线性不等式约束。
1.2.2.2 电池电量约束
储能电池的电量有上限SOCmax,下限SOCmin,为了方便讨论,将电池放电至下限的状态等效为电池电量为0,而充电达到上限等效为电池充满的状态。后文在讨论电池容量时默认为有效容量,放电深度在成本计算中纳入。电池充放电时,其电量满足:
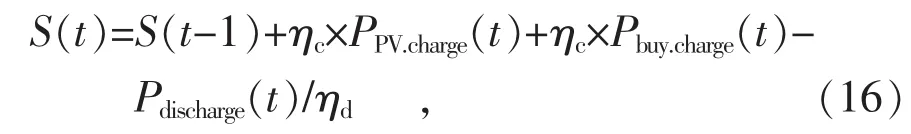
式中:ηc=ηd=0.98,为电池充放电效率,即电池电量为1 h前的电量加上这小时内的充放电量。由于电池容量始终在额定范围内,有:

将式(16)代入式(17),可确定 2组线性不等式约束,即:
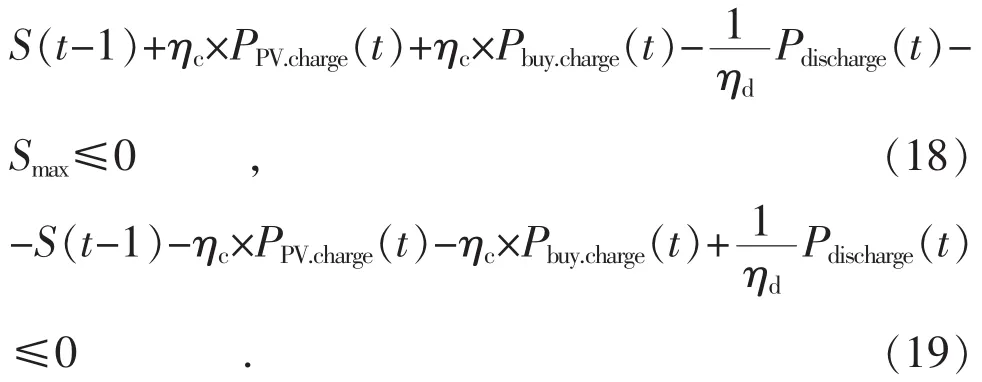
可以看出,每个时刻的电量约束不等式继承了前1 h的参数的系数,而为了避免每日电池的剩余电量对后一日的程序规划造成影响,需要在每天结束时将电池电量重置为0,因此每24 h不等式的系数会清零,也可以表示为电池每日的初始电量 S(0)为 0, 即:
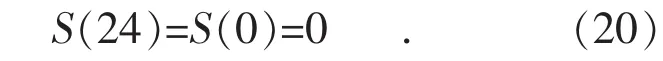
在程序中,以一月典型日为例,用x(n)代替相应优化参数,式(20)可写为:
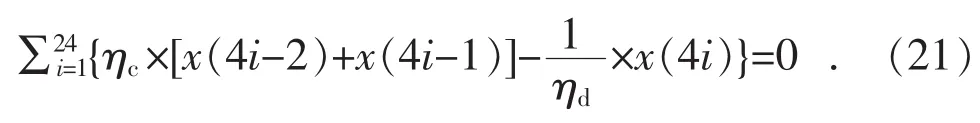
值得注意的是,在考虑了电池充放电效率后,式(12)和(13)所表示的电池充放电不同时进行的约束就可以删去,因为在最优化的条件下,电池不会试图同时进行充放电,优化程序中可以不考虑该非线性不等式约束。
电池容量和功率Smax和的取值范围设为大于0且小于一个足够大的常数。式(20)可表示为fmincon函数的线性等式约束,式(18)和(19)为线性不等式约束。
若设备运行过程中电池充放电过于频繁,会缩短电池所能使用的时长,因此需要对电池的充放电次数进行约束。为了降低计算的复杂程度,不考虑容量衰减,用式(22)来近似表示每天电池约进行1次充放电循环:
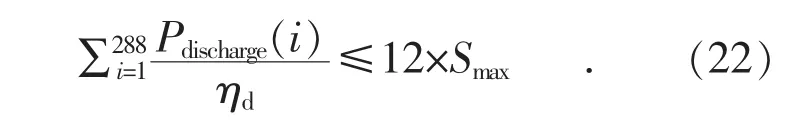
式(22)在优化模型中表示一个线性不等式约束, 其中参数 x(4i)的系数为 1/ηd, x(1153)的系数为-12,该约束避免了电池充放电过于频繁而导致电池寿命过短所带来的不利影响。
1.2.2.3 目标函数
园区光伏储能系统的经济效益作为主要的关注对象,直观地体现在系统全年费用支出上,因此将其作为目标函数(若费用支出为负值,说明系统每年可获得电费收益)。由于储能电池的投资为一次性支出,目标函数中的全年费用支出为:将电池投资成本在一个寿命周期内按年分摊后,再加上购电、售电费用及补贴的总费用。光伏及储能设备的维护成本与电费和投资成本相比很小,可以只考虑电费支出Copex和投资成本Ccapex。
园区每小时电费支出为购电电费减去光伏发电补贴与光伏上网收入,即:
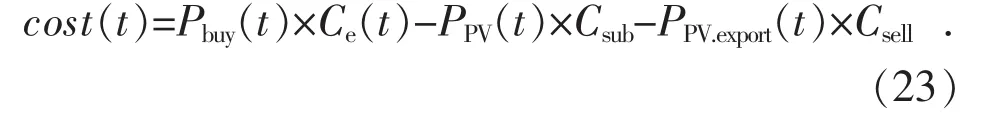
据此可以求得每月典型日电费支出,并根据每月天数将其换算为全年电费支出Copex。
储能电池的投资成本Ccapex分为配置容量的成本costbattery.cap和配置功率产生的成本costbattery.power,根据实际情况,可在程序中对电池成本的计算过程进行修改,这里仅进行较为初步的计算。
配置容量的成本costbattery.cap为电池容量和单位容量的投资成本的乘积,考虑到所选用的锂电池放电深度为90%,则:

配置功率产生的成本costbattery.powe主要为满足功率要求的PCS双向变流器成本,本例中PCS变流器的超负荷率约为1.0,PCS双向变流器功率与选取的电池最大充放电功率Pmax相同,配置功率产生的成本costbattery.power为变流器功率与单价的乘积,即:

为了将储能设备初始投资总费用转化为电池在整个寿命周期内每年的平均投资成本,引入资金回收系数:
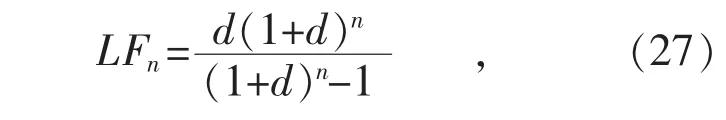
式中:d为折现率,其取值会影响到最终的配置结果,这里d取较为常用的值0.06;n是储能电池的寿命年限,园区选用锂电池在整个寿命周期内可进行约4 000次完整的充放电循环,按照之前约束条件中平均每天1次充放电循环计算,n可取值为11,即11年后需要更换新的电池。后文将对折现率和电池寿命对储能电池配置结果的影响进行简要分析。
因此目标函数即园区全年总费用支出为:
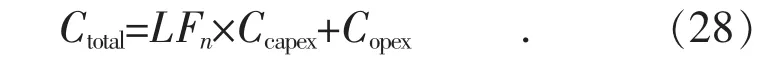
文中所述1 154个优化参数在288 h里的线性不等式约束共1 729个,相应优化参数的系数保存在大小为1 729×1 154的矩阵A中;每日结束时电池电量为0即线性等式约束共12个,保存在大小为12×1 154的矩阵Aeq中。将优化参数、约束条件和目标函数加入fmincon优化函数中,在此基础上建立系统模型,编写优化程序。
针对储能电池进行优化配置的思路大致如图5所示。

图5 优化模型程序
需要输入的数据包括3部分:系统年负荷及光伏出力预测数据、分时电价及光伏补贴和并网价格、电池相关参数及容量和功率的投资成本。
运行优化程序可以得到:最佳经济效益的电池容量和功率配置结果;最优化的电池充放电策略下全年288 h系统购电售电功率和电池充放电功率;系统全年的费用支出和储能电池投资的内部收益率IRR、光伏自我消纳率SCR的数值。
2 优化结果分析
将处理为288 h数据的园区全年低方案负荷预测数据、光伏出力数据、电价数据导入优化程序,光伏上网电价参数设置为0.451 5元/kWh,度电补贴为0.42元/kWh,园区所选用的储能电池报价为每兆瓦时容量成本250万元,每兆瓦功率成本100万元。
程序运行结果为电池容量和功率配置均为0,说明此时由于电池投资成本较高,引入电池储能将无法收回投资成本。当前电池储能的成本逐年降低,为了探究电池优化配置和经济效益与电池成本的关系,假设电池容量和功率投资成本按相同的比例降低,通过修改优化程序的参数,其余数据保持不变,可以得到一组电池容量和最大充放电功率大小随电池成本变化的结果,以及相应用IRR来衡量的储能电池经济效益,如图6所示。
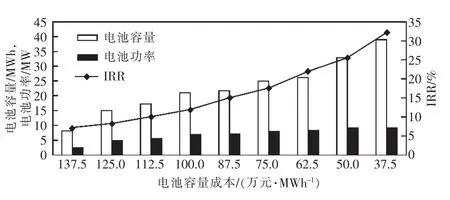
图6 电池配置容量、功率及经济效益与电池成本关系
很明显,电池投资成本降低,可配置的电池容量和功率也随之增加,其经济效益也越加明显。而优化结果中得出的各部分功率的具体数值可以反映出系统的功率流动情况,以3月的典型日即月平均数据为例,当电池容量成本为100万元/MWh时,园区加装储能电池并经过优化后,系统各部分功率如图7所示。
图7显示了1天时间内电价和负荷功率的变化情况,以及光伏出力、电池充放电及从电网购电功率的变化和相互关系,其中负荷曲线是原始负荷减去园区CHP出力的结果。储能电池在夜间电价低谷时段充电,并在之后的电价高峰时段放电,减少此时的购电电费支出。可见此时电池储能在系统中发挥了峰谷差价套利的作用。
图7中的电池容量成本下降为50万元/MWh后,电池容量增加幅度较大,但所配置的电池功率则增长较不明显。主要原因是该光伏储能系统中,电池放电全部用于满足园区负荷,若电池充放电功率配置过大则不能有效利用,造成浪费。例如,将电池容量成本改为50万元/MWh,3月的典型日各部分功率如图8所示。
图8中电池放电功率受到负荷需求的限制,当日18:00后负荷需求完全由电池放电满足,而放电功率不能超过负荷功率,同样地,电池容量也会受到日负荷总量的限制,与此同时,加装电池不增加系统购电峰值这一约束条件也限制了电池容量的增长。可见,即使在电池成本很低的情况下,应配置的容量和功率也不是越大越好。
除了电池成本的下降,光伏发电补贴政策也逐年改变,光伏上网电价也呈下降趋势,光伏每度电的补贴也逐渐减少甚至会被取消。显然,光伏补贴的下降会降低系统的经济效益,但对储能电池的充放电策略和规划不产生影响;而光伏上网电价将会对电池的充放电策略和系统的功率流向产生影响。
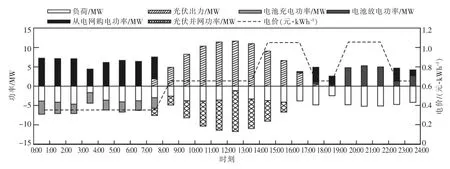
图7 电池成本为100万元/MWh时3月典型日系统功率
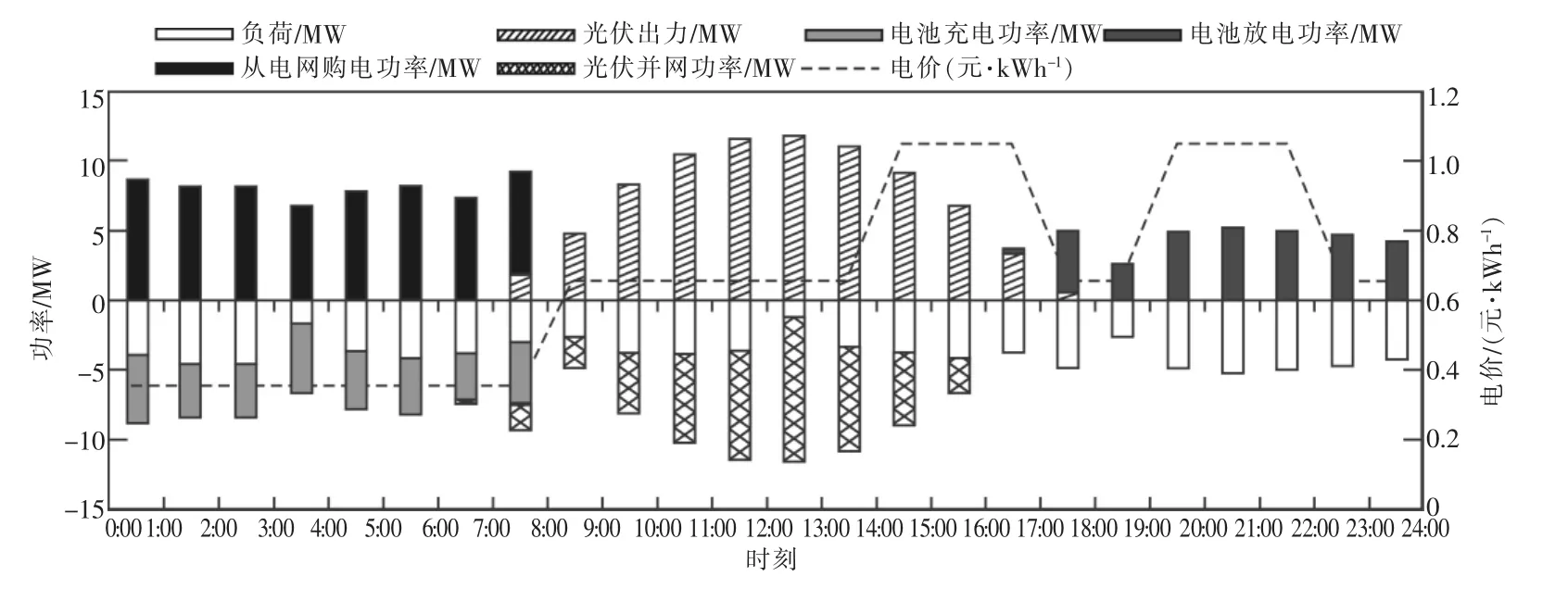
图8 电池成本为50万元/MWh时3月典型日系统功率
以电池容量投资成本为100万元/MWh的情况为例,修改优化函数中光伏上网电价参数,可以得到在并网价格从目前的0.45元/kWh逐渐降低至0.25元/kWh的过程中,电池容量和功率的配置大小以及光伏自我消纳率的SCR变化趋势,如图9所示。

图9 电池配置容量、功率及SCR与光伏上网电价关系
本例所采用的分时电价用电模式里,谷段电价为0.352 2元/kWh。从图9可以看出,光伏并网电价的变化对储能电池的配置影响不大,但并网电价由0.37元/kWh下降到0.35元/kWh时,光伏自我消纳率SCR值由41.4%提升到64.9%,出现了明显的跃升,说明此时系统的功率流向发生了改变。并网电价为0.35元/kWh时,系统3月的典型日功率如图10所示。
对比图7和图10,可以看出:当并网电价低于谷段电价时,系统更倾向于由光伏为电池充电,光伏发电并网的部分也相应减少,可见,储能电池有效地发挥了提高光伏自我消纳能力的作用。同时,本例中的光伏出力的数值较高,而负荷则相对较低,因此光伏除满足负荷外,还有充足的剩余部分用于电池充电。如果光伏出力相对负荷更低,在此基础上,将光伏出力降低50%,当日的功率流动则如图11所示。
此时储能电池除了利用光伏充电,也在夜间谷段电价时段充电。与图10对比,可以看出并网电价低于谷段电价时,光伏充电的优先级更高,光伏不足时才需要购电进行充电,而并网电价高于谷段电价时的优先级与之相反。
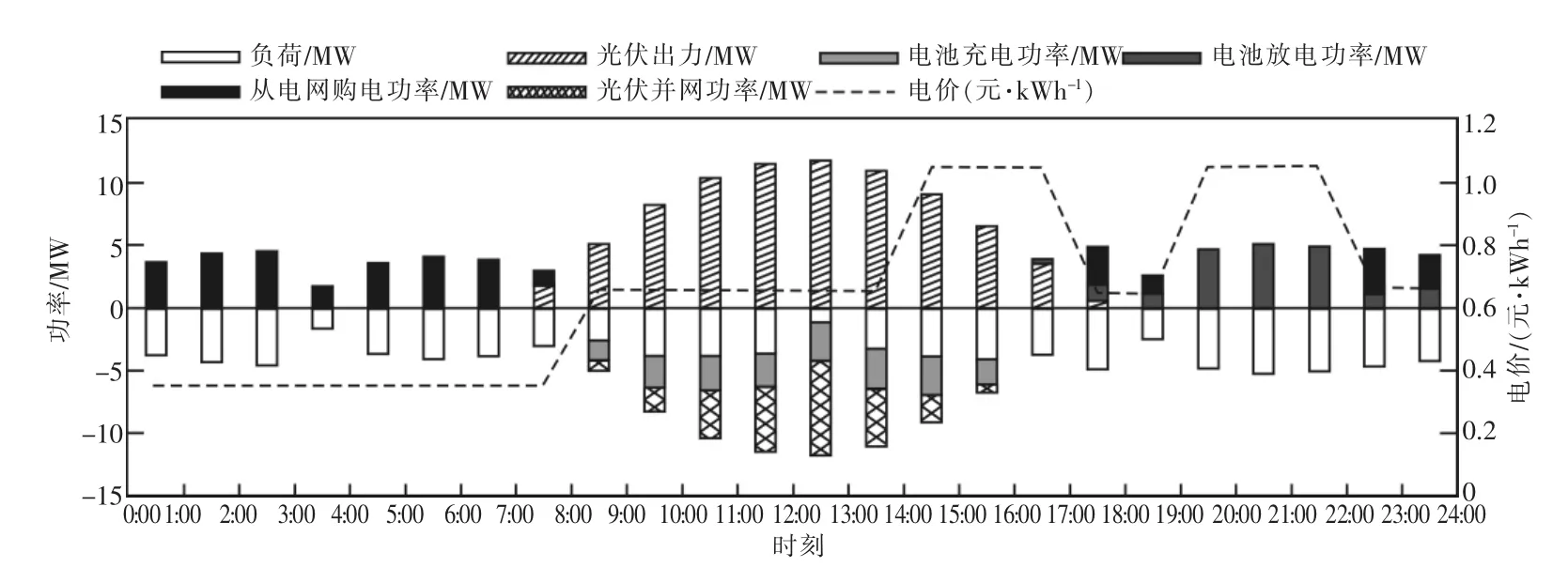
图10 并网电价为0.35元/kWh时3月典型日系统功率
在之前的优化程序中,默认电池寿命为11年,折现率为6%,但这2个参数也具有不确定性,并会对储能电池优化配置的结果产生影响。当电池容量成本为100万元/MWh,并网电价为0.451 5元/kWh,折现率为6%时,图12显示了电池寿命在10~24年的范围内,储能电池的配置结果和内部收益率IRR与电池寿命的关系。
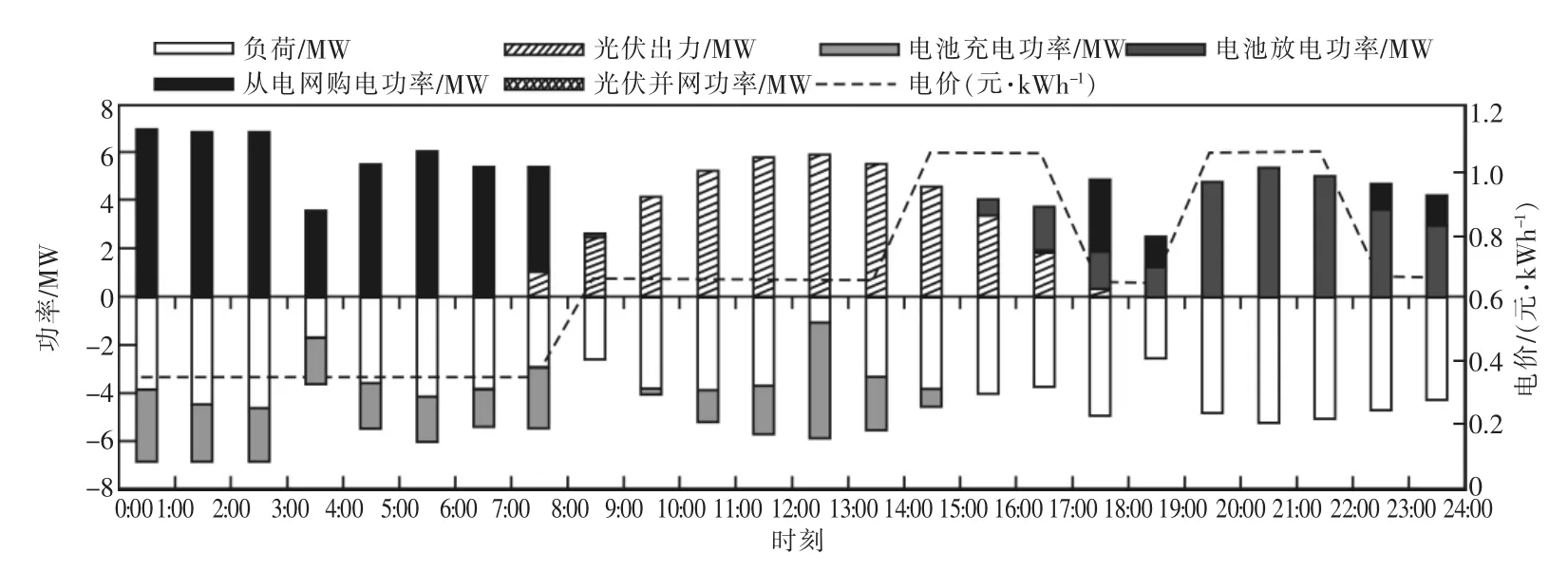
图11 光伏出力减半时3月典型日系统功率
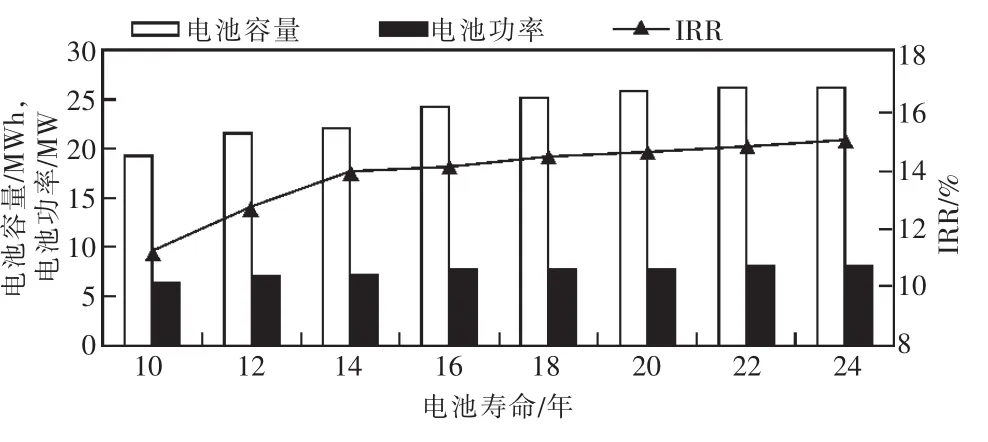
图12 电池配置容量、功率及IRR与电池寿命关系
从图12可以看出,随着电池寿命的提升,优化配置的电池容量和功率有小幅度的增大,但电池初期投资成本也因此上升,使得IRR在图中后半部分的提升并不明显。因为增大电池容量和功率获得年收益增加的同时,也会引起电池初始投资成本的增加。
图13则反映了电池的容量和功率配置结果及IRR与折现率的关系,其中电池容量成本为100万元/MWh,并网电价为0.451 5元/kWh,电池寿命为10年。在折现率从3%提高至7%的过程中,IRR呈现出上升趋势,其主要原因是配置的电池容量和功率的降低减少了电池的初始投资成本,因而使IRR出现了上升。折现率为3%时,IRR与折现率之差为7.6%;折现率为5%时,IRR与折现率之差为5.8%;折现率为7%时,IRR与折现率之差为4.6%。可见随着折现率的增加,储能的投资收益逐步减弱。
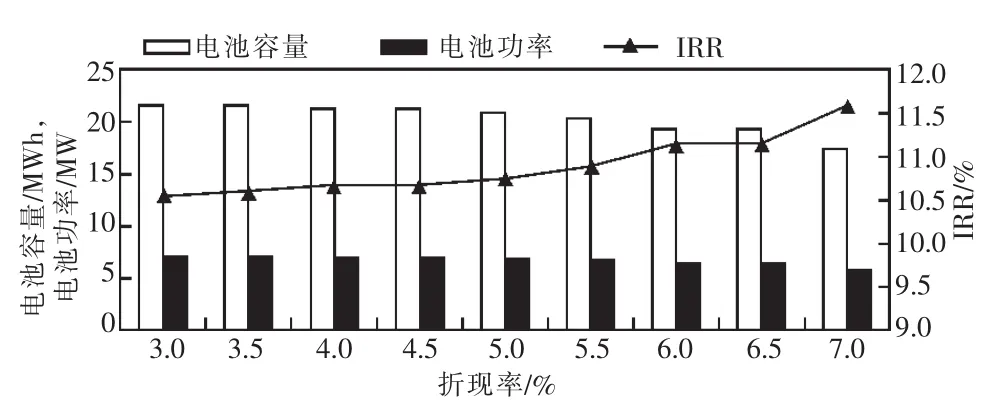
图13 电池配置容量、功率及IRR与折现率关系
3 结语
通过对光伏-储能系统建立线性整数规划模型,对园区光伏储能系统中的电池容量、功率及系统全年电池充放电功率、购电售电功率等参数进行统一的优化计算,得到了最优化的电池充放电策略及电池配置方案,并分析了配置结果随电池成本、光伏上网电价、电池寿命与折现率的变化规律以及储能电池在系统中发挥的作用。
当前储能电池的投资成本较高,且电池寿命有限,园区加装储能电池难以收回投资成本。但随着电池价格的降低,储能电池将带来明显的经济效益。在光伏发电补贴以及光伏上网电价逐年降低的背景下,光伏发电带来的收益会有所下降,但电池储能系统仍然能有效提升经济效益。
当光伏并网电价高于谷段电价时,储能电池优先在电价低谷时从电网购电进行充电,电价高峰时放电进行峰谷差价套利,光伏给电池充电的优先级较低且电池放电功率不应超过负荷功率;当并网电价低于谷段电价时,储能电池优先由光伏充电,光伏不足时在电价低谷时购电充电作为补充,此时储能电池可以提高系统的光伏发电消纳能力。
本文的优化计算中电池主要进行峰谷差价套利以使经济效益最大化,但储能电池在系统中所发挥的作用是多样的,也具有多种盈利渠道,如可将储能电池用于削峰填谷,进行需量电费管理,或用于动态增容,以及需求侧响应。这些新的模式带来了哪些新的约束条件,如何量化这些收益,并将其纳入到优化模型的目标函数中,以及对光伏与储能的耦合和电池充放电策略所产生的影响,是今后需要进行研究和完善的主要内容。约束条件的增加使系统模型更加复杂,且优化程序的运行也会更加耗时,因此如何提高程序的运行效率也需要在后续工作中加以关注。随着技术的进步,光伏储能系统的优势会更加明显。

