“细胞增殖”教学中的数学模型应用举例

陈廷华

(江苏省无锡市辅仁高级中学 无锡 214123)

“细胞增殖”内容是高中生物学课程中学生理解生命本质、进行科学思维、形成生命观念的重要版块，无论是新课教学还是专题复习，都有许多绕不开的教学难点，不仅是知识内容本身微观抽象，概念名词多，现象特征复杂，而且要在动态的变化过程中理解染色体、染色单体、着丝点等概念的相互关系及物质的数量变化规律，需要经历抽象、概括、判断、推理等复杂思维过程。所以机械的识记不可能理解生命规律的本质，对枯燥的数字必然是记不牢、记不长、记不清，学生感到难学。有效地组织学生综合运用分析与比较、归纳与概括、演绎与推理、模型与建模等方法进行科学的理性思维，阐释生命现象及规律，可以化被动为主动。物质的数量变化的最佳阐释是数学模型，如何巧妙建构、变换和使用数学模型，如何将数学模型用在当用之处，以达到最佳教学效果？现通过几个教学实例加以阐述。

1 利用数学模型的推演，认识细胞增殖的生物学意义

多细胞生物体体积的增大，既靠细胞的生长增大细胞的体积，还要靠细胞分裂增加细胞数量，这是因为细胞不能无限长大。细胞为什么不能无限长大？人教版必修1教材提供了一个模拟探究实验，探讨细胞大小与物质运输的关系。实验原理和操作过程比较简单，但是对实验现象的讨论及规律的认识却有相当的思维力度，需要进行数学模型的推演，并要用联想把推演的结果迁移到细胞中，认识物质运输的效率与细胞大小的关系。教学程序包括： ①学生按教材实验步骤完成实验操作；②将实验现象填入表格；③引导学生根据实验数据思考讨论，循序渐进进行数学推演。琼脂块边长越大(琼脂块越大)，表面积、体积、表面积/体积如何变化？→琼脂块越大，NaOH扩散深度、NaOH扩散体积/琼脂块体积如何变化？→琼脂块越大，NaOH扩散速度、NaOH扩散效率如何变化？为什么？(提示： NaOH扩散速度、NaOH扩散效率分别用什么指标表示？)→NaOH扩散效率与表面积/体积之间呈何相关？(提示： 表面积/体积与NaOH扩散体积/琼脂块体积之间呈何相关？)→总结： 琼脂块大小与表面积/体积、NaOH扩散效率之间有何关系？→大多数高等动植物细胞的直径为20～30μm，请计算细胞的直径分别为20μm和30μm的细胞表面积/体积？→如果把琼脂块换成高等动、植物细胞，则物质运输的效率与细胞大小之间是什么关系？→请推测： 多细胞生物体内细胞具有怎样的生命历程？

学生通过推演，自己得出了结论： 细胞越大，细胞表面积/体积越小，物质运输的效率越低，所以，当体细胞生长到一定大小时，要么进行细胞增殖，要么走向分化、衰老、凋亡等，这是生命规律的必然，也是生命的高效性、结构与功能的统一性等生命观念的体现。有些教师想当然认为该结论比较简单，不需要做实验，更不必做复杂的数学推演，直接把结论告诉学生。这种做法是不合适的，没有动手实验，就缺少感性认识，就缺少生物学概念的形成和观念的建立的根本途径；没有分析探究的过程，就失去了一次较好的科学思维训练，都不利于激发学生后续学习的兴趣。

2 紧扣数学模型转折点的含义，辨析细胞分裂各时期

用坐标曲线图表示细胞分裂各时期物质的动态变化过程简单而直观，但是简单的曲线所代表的生物学含义并不简单，让学生借助简单的数学模型深刻理解细胞分裂各时期生物学含义是教学的重要目标，也是教学的难点。怎样才能让数学模型蕴含的生物学含义“显而易见”呢？教学实践表明，紧扣坐标曲线转折点的含义，引导学生学习和思维，可以化难为简，突出重点。

以细胞分裂过程中染色体数目的变化教学为例，示例如下： ①列出有丝分裂过程中各时期染色体数目(以体细胞染色体数2N为例)；②画出有丝分裂各时期细胞中染色体数量变化曲线(图1)；③分析重要的转折点D→E、 F→G、 H→Ⅰ代表的生物学含义分别是什么？④据图2分析减数分裂各时期细胞中重要转折点F→G、 I→H、 L→M的生物学含义？⑤分析图1中D→E与图2中I→H有何共同点？⑥分析图1中H→Ⅰ与图2中F→G的变化有何本质不同？⑦分析图1和图2各段分别代表什么时期？

通过对曲线转折点、关键阶段的分析，进行综合比较、判断、推理，学生能深刻理解细胞分裂的重要时期的生物学变化，即有丝分裂后期和减数第二次分裂后期着丝点分裂，姐妹染色单体分开，染色体加倍(相对于前一时期)，减数第一次分裂同源染色体分离并平均分配给2个子细胞导致染色体数目减半。抓住了关键阶段，抓住了重点，突出了本质，再去辨析其他各时期就轻松自如了。

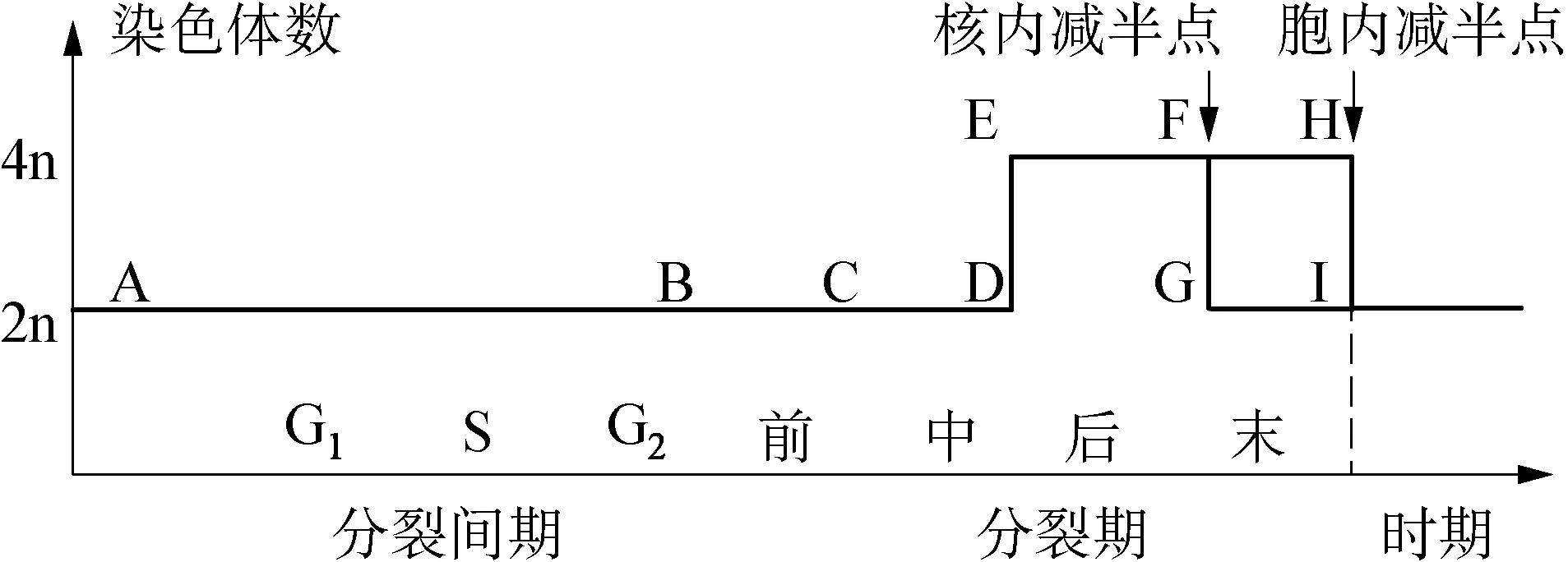
图1 有丝分裂各时期细胞内染色体数目的变化

图2 减数分裂各时期细胞内染色体数目的变化

参照此法，分析细胞分裂各时期核DNA数量的变化，无需死记硬背，同样可以做到心知肚明，一目了然。

3 变换数学模型的坐标含义，理解重要概念的相互关系

细胞分裂过程中，染色体、染色单体、核DNA的数量关系是不断变化的，1个染色体上可能是2个DNA，也可能是1个DNA，关键是染色体上是否存在染色单体，本质上涉及到染色体的复制和着丝点分裂2个重要过程，如何在动态的变化过程中理解概念间的相互关系？笔者经验是： 可以对同一物质从不同的角度变换数学模型的坐标含义，进行反复比较，对比分析坐标曲线的异同，从而明确概念间的本质联系。例如对核DNA，可以从“细胞中核DNA数”“每条染色体上的DNA数”“染色体与核DNA比值”“有丝分裂中的DNA数”“减数分裂中的DNA数”等不同角度构建数学模型，分析比较。教学程序包括： ①画出有丝分裂过程中每条染色体上DNA的含量变化曲线(图3)；②根据有丝分裂过程中每条染色体上DNA含量变化曲线分析ab和cd的含义；③如果纵坐标表示有丝分裂染色体与核DNA的比值，画出变化曲线(图4)，分析ab和cd的含义；④横坐标表示有丝分裂各时期，则图3和图4的bc、 de分别代表哪些时期？如果横坐标表示减数分裂各时期，则bc、 de分别代表哪些时期？(易错点： bc可表示减数分裂第一次分裂和减数第二次分裂的前期和中期，往往易忽略减数第一次分裂)⑤如果图3纵坐标表示细胞有丝分裂核DNA含量变化，则bc、 de分别代表哪些时期？(易混淆： 与细胞中每条染色体上的DNA的数量变化混淆，因为数学模型相同，但表示的时期不完全相同)通过坐标含义的不断变换，让学生画图分析，引导学生举一反三、由浅入深、由表及里去认识细胞分裂的实质： 染色体上DNA经过复制后，DNA加倍，随着着丝点的分裂，姐妹染色单体分开，加倍的DNA最终可以平均分配给2个子细胞。

图3 细胞分裂各时期每条染色体DNA含量

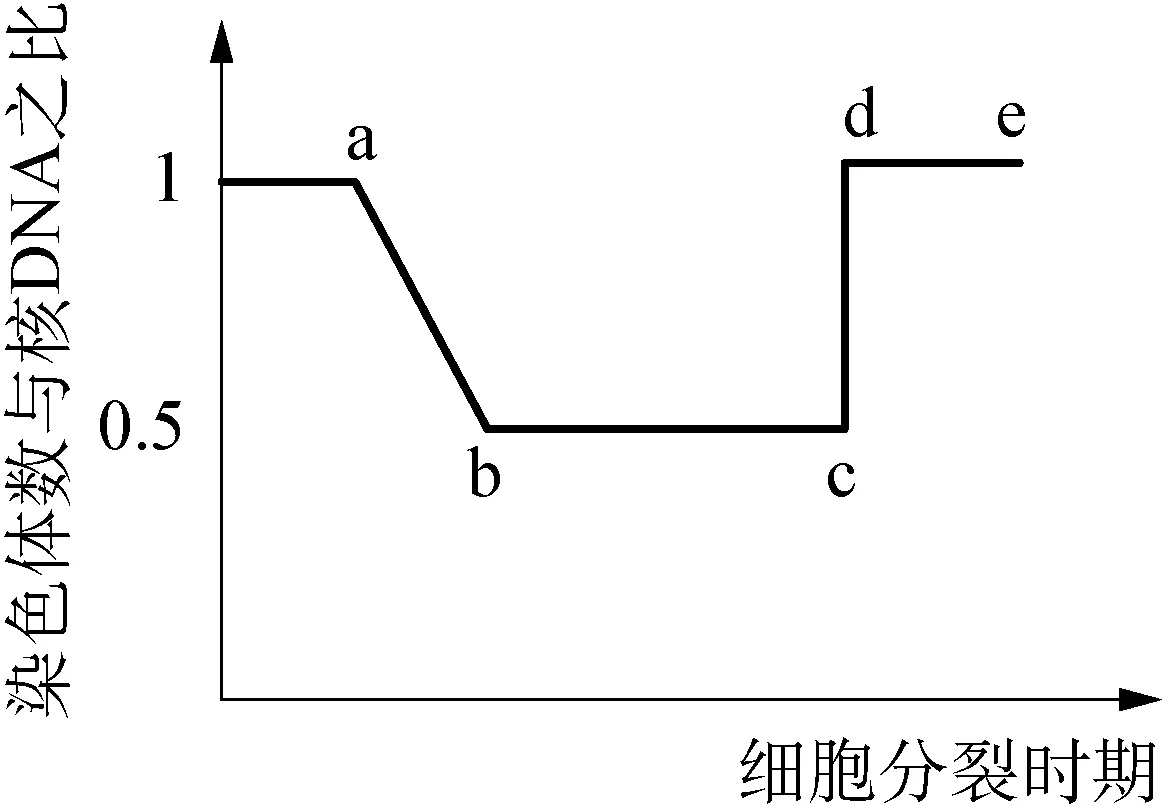
图4 细胞分裂各时期染色体与核DNA比值

同时通过模型含义的变换，构建数学模型，分清易错易混淆的知识，学生学得轻松，有满满的成就感。

4 利用数学模型的形式转换，掌握细胞分裂过程中物质数量变化规律

数学模型有数学方程式、曲线图、柱状图等多种形式，各有其优点和不足。例如，在同一坐标系下画出染色体、核DNA、姐妹染色单体的数量变化曲线，能够反应相关物质的连续的、动态的变化过程，同时便于分析比较一些关键阶段的染色体变化，但是在比较物质变化所对应的时期时，则反而显得凌乱，如果换成柱状图(图5，以有丝分裂为例)，则更能直观地看出有丝分裂过程中核DNA何时加倍，为什么加倍？染色体何时加倍，为什么加倍？染色体、核DNA何时减半，为什么减半？染色单体和核DNA之间的数量关系？

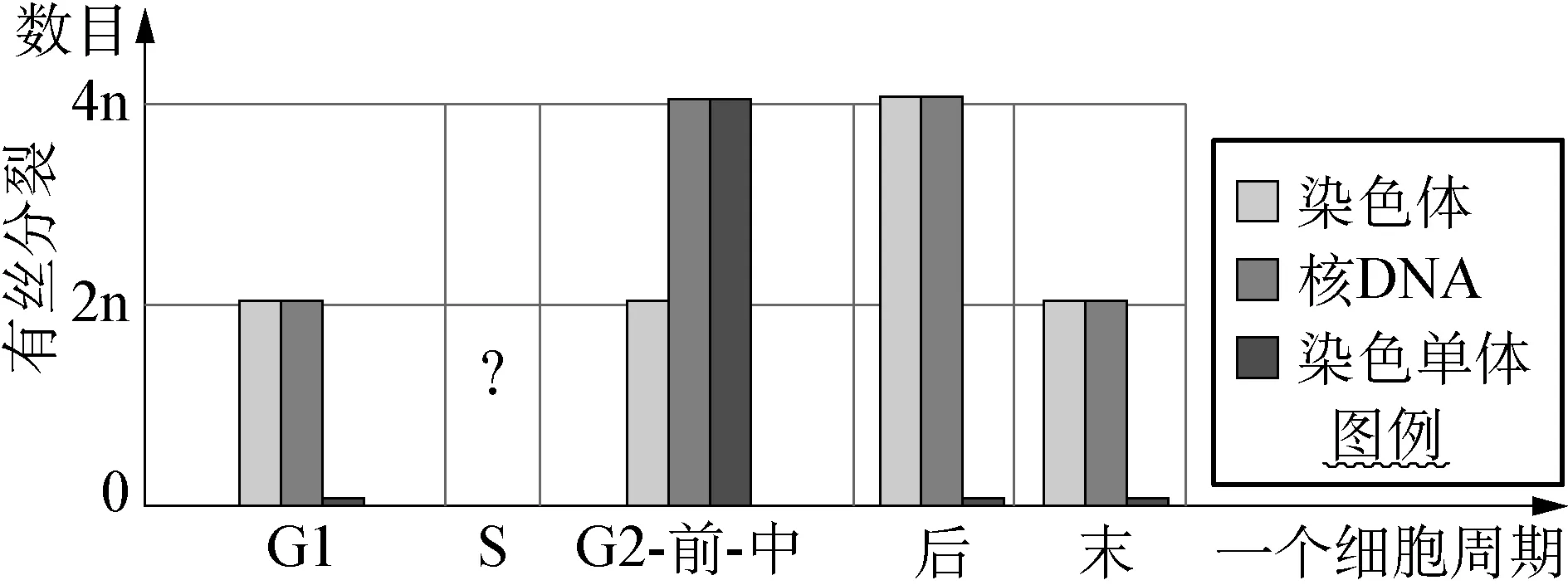
图5 有丝分裂过程中染色体、核DNA、染色单体变化

熟练运用合适的数学模型阐述生命现象和规律是科学思维能力的重要体现，在“细胞增殖”的教学中，要充分利用好细胞分裂图像、曲线图、柱状图等多种形式进行信息转换，再现重要概念，让学生分析表述，判断推理，培养学生综合思维能力。

教学示例如下： 下列是科研人员对某动物(2n)细胞有丝分裂和减数分裂过程中染色体形态、数目和分布的观察分析结果，其中图6为其细胞分裂一个时期的示意图(仅示部分染色体)，图7是依据不同时期细胞中染色体数和核DNA分子数的数量关系而划分的细胞类型，图8是细胞分裂过程中染色体数目变化。

图6 细胞分裂某时期

图7 细胞类型

图8 细胞分裂中染色体的数目变化

教师可以分四步引导学生进行分析、判断、推理。

第一步： 逐一分析图形、曲线、柱状图的重要特征，认识细胞分裂各时期。

重要特征分析： 图7——着丝点分裂，代表何时期？图8——柱状图染色体与核DNA的二种数量关系分别对应哪些时期？图8——转折点(时段)②、④、⑥的生物学含义？

分析解答问题： 图7中细胞分裂的方式和时期是有丝分裂后期，它属于图8中类型为a的细胞。若某细胞属于类型c，取自精巢，没有同源染色体，那么该细胞的名称是次级精母细胞。

第二步： 重点分析图8中染色体与核DNA的数量关系，理解数量变化规律。

a——着丝点分裂，染色单体分开，染色体数=核DNA数=4n，为有丝分裂后期；c——着丝点分裂，染色单体分开，染色体数=核DNA数=2n，为MⅡ后期；b和d都有染色单体，但染色体数量不同，b表示有丝分裂前期、中期或MⅠ，d则表示MⅡ前期、中期。

分析解答问题： 若类型b、 c、 d、 e的细胞属于同一次减数分裂，那么三者出现的先后顺序是b、 d、 c、 e。

第三步： 在图文与模型转换中再现重要概念，如同源染色体等。

由于图8的b表示有丝分裂前期、中期或减数第一次分裂，c、 d、 e表示MⅡ相应时期，所以在图8的5种细胞类型中，一定具有同源染色体的细胞类型有a、 b。

第四步： 综合分析图形、柱状图与曲线图的含义，紧扣物质数量变化，进行意义关联，归纳判断。

着丝点分裂导致图8中一种细胞类型转变为另一种细胞类型，其转变的具体情况有b→a、 d→c(用图中字母表述)，分别对应于图8中的②、⑥(用图中序号表示)。

实践表明： 有效地利用数学模型进行“细胞增殖”内容的教学，可以实现难点不再难，重点更突出，学生学得轻松，学得有效。