施工顺序对地铁隧道开挖变形影响研究

韩丽媛，汪海波，王松青，宗 琦

(1.安徽理工大学土木建筑学院，安徽 淮南 232001；2.中煤矿山建设(集团)城市交通建设分公司，安徽 合肥 230091)

地铁建设过程中，隧道的开挖会造成围岩的应力重分布产生位移[1-2]。较大的位移会引起沉降和大变形，甚至造成地表塌陷、建筑物倒塌[3-5]。因此地铁隧道的变形问题是关系建设安全和进度的关键问题[6-8]，为避免隧道工程开挖对周围地层产生不良影响，必须对地层沉降和变形进行有效的预测，从而合理控制隧道开挖引起的地层沉降。

有限元数值模拟软件可以根据实际工程地质条件、施工方法、选择对模拟条件进行设置，利用计算机技术和数值分析的方法进行有效的数值模拟，预测隧道开挖变形，因此得到广泛应用[9-10]。文献[11]采用PLAXIS软件模拟研究了固定埋深、单一围岩下的不同净距对中夹岩核心区受力影响以及同一平面上拱顶地表沉降、拱顶及拱底的位移；文献[12]基于Gibson土建立隧道三维实体结构计算模型，研究平行双孔隧道异步开挖的滞后距离对两隧道同一平面间隔相同角度各点的位移；文献[13]采用模拟实验研究小净距隧道施工过程中的相互影响，并用数值模拟的结论作为对比参考。文献[14]运用MIDAS GTS建立三维模型模拟了某地铁工程正线盾构下线明挖区间的开挖过程，分析了土体变形对上部明挖区间的影响。

武汉市轨道交通27号线一期项目是江夏区首条地铁线路，由于青龙山地区覆土层逐渐减小，该线路纸坊大街站-地铁小镇站正线区间暗挖隧道采用矿山法施工。由于线路从纸坊大街站出来后隧道间距小，地表为城市道路和居民区，覆盖层为黏土和中风化石灰岩，且隧道顶板处于岩土层分界面、上覆石灰岩厚度较薄，故建立非单一围岩的实体三维模型，分析净距和异步开挖对隧道变形的影响，以控制开挖步距，为周边地铁隧道施工提供参考。

1 工程概况

纸坊大街站-地铁小镇站正线区间暗挖隧道和出入场线并行，区间起点里程DK0+074.200。出入场线位于正线区间左、右线之间，并线段出入场线与正线最小净间距1.64m(净岩柱)。出入场线净宽11.8m，净高9.6m。左右隧道净宽6.98m，净高7.401m。各隧道及地面道路位置关系如图1所示。

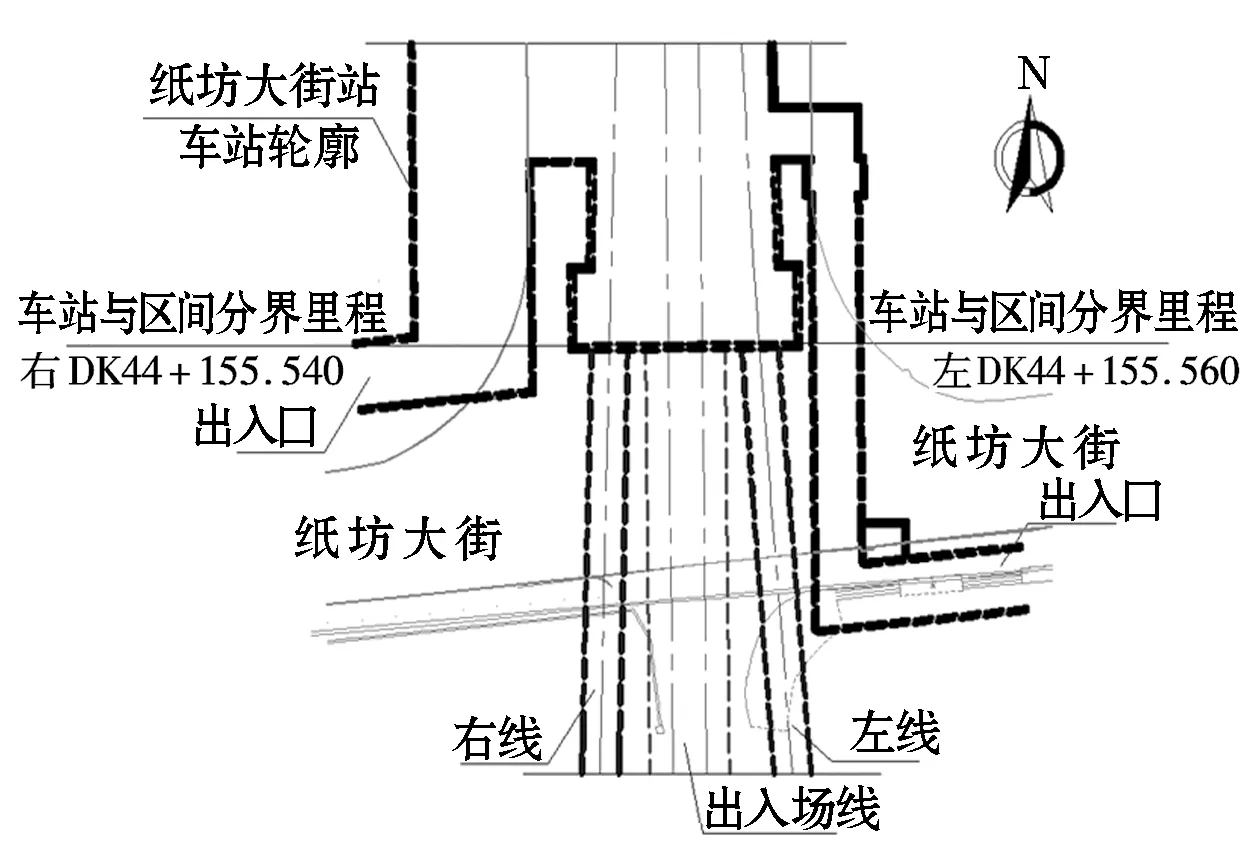
图1 隧道间平面位置关系

该区段主要穿越中风化石灰岩，上覆土层主要是红粘土、杂填土、粉质黏土、粘土夹碎石。隧道下穿青龙山，基岩埋深较浅，裂隙发育，入渗条件好，接受大气降水补给后，侧向径流补给场区地下水，径流条件较好，施工期间降水量较少，地下水水位较低，水量相对较小，具有明显的动态特征。

2 数值计算方案

2.1 数值计算模型

由于已定出入场线待左右线隧道永久衬砌施做后再行开挖，模拟计算选取实际工程中左右隧道开挖、支护过程进行研究，忽略出入场线开挖。根据设计情况，隧道顶板埋深19.6m，利用ANSYS建立模型，原点在两隧道净距中点处，长91m，宽47m，沿开挖方向取50m。其中左右边界各取30m，下边界为20m，两隧道实际净距为15m。对于模型位移的边界[15-17]，对其左右施加水平方向力的约束。对于力的边界，仅考虑土体的自重，取重力加速度g=9.8 m/s2。

计算采用D-P本构模型，岩土体采用solid45单元，支护结构采用shell63单元，采用Mesh200单元建立岩土体的面模型和支护的线模型，然后将线模型拉伸为壳模型，面拉伸为体模型。

2.2 数值计算方案

为研究净距和不同超前距离开挖时隧道的变形特征，结合工程特点，净距设计为1.64m、3m、9m、15m四种，超前距离设计为0m、10m、20m、30m、40m、50m六种；共24种计算工况。

上层覆盖简化成厚度均匀变化的土层。模拟时对锚杆支护采取简化处理，将隧道左右两侧围岩的物理力学参数提高为C25混凝土，其加固厚度为0.9～2.5m均匀变化，做二次衬砌与开挖时间间隔较久，所以二次衬砌的作用效果不予考虑[18]。左右隧道的开挖采用全断面一次开挖，每次开挖2m后，施作初期支护，包括喷射350mm厚C25混凝土和边墙安装3.5mφ25中空注浆锚杆，环纵向1m×0.5m。左线隧道先行开挖，等开挖至预设超前距离时再进行右线隧道开挖。为研究拱顶、拱腰和地表沉变形，沿左隧道开挖方向10m每2m选取一个监测断面。

2.3 数值计算参数

根据岩土工程勘察报告，采用的各岩土层及喷射混凝土的基本物理力学参数如表1所示。

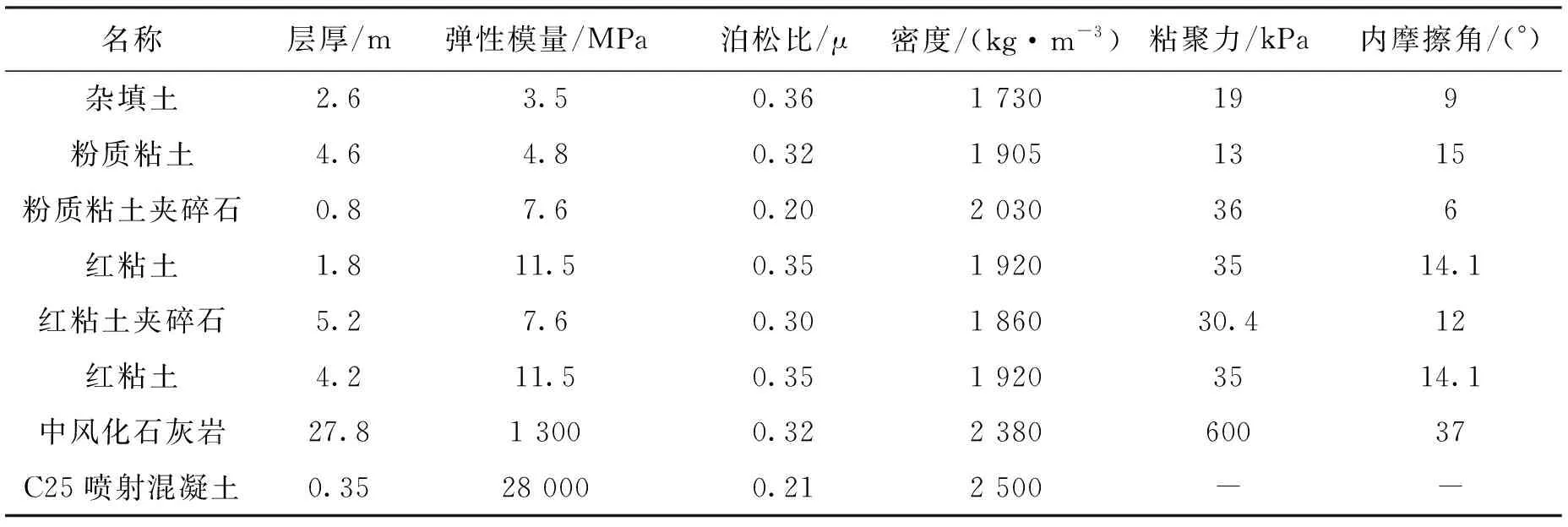
表1 岩土体和喷射混凝土参数

3 数值计算结果与分析

3.1 小净距隧道开挖地层位移分布特征

由于设置的工况种类较多，仅列出净距1.64m超前0m和10m时的位移云图，如图2所示。

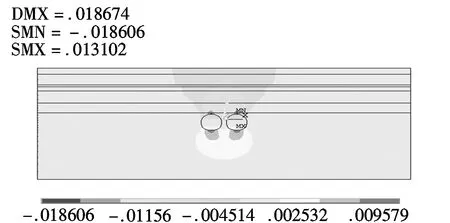
(a)超前0m时地层位移云图

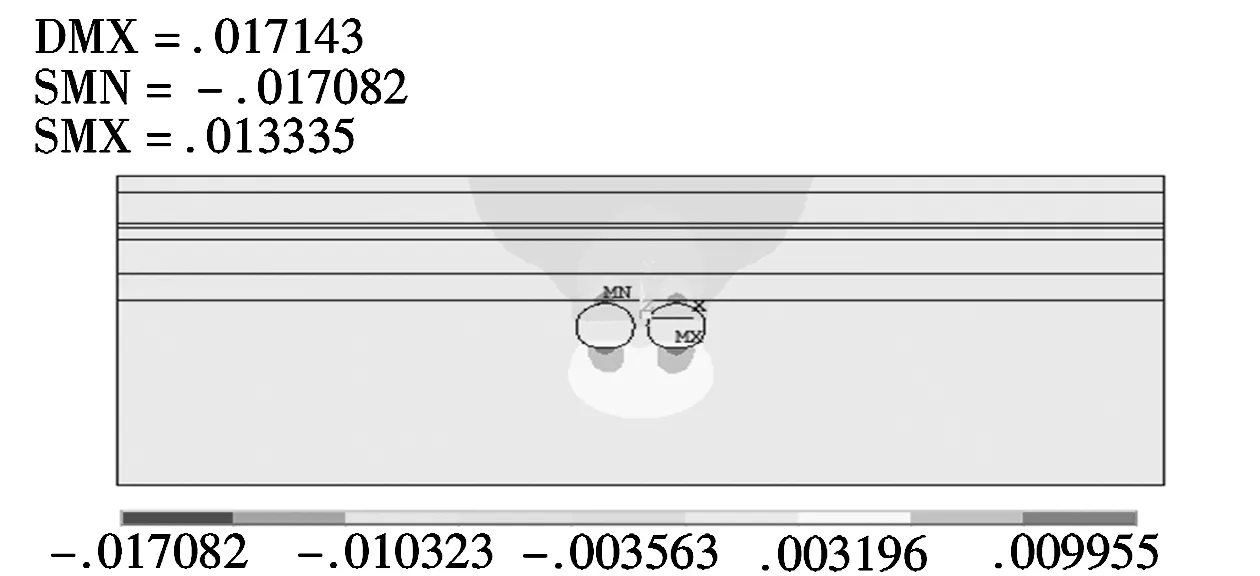
(b)超前10m时地层位移云图图2 小净距隧道开挖地层位移分布

由图2可知，两种开挖方式地层位移分布特征相似，最大沉降量都在拱顶，分别为18.6mm和17.08mm；最大隆起量在拱底；且图2(a)的地层沉降宽度和沉降量均大于图2(b)，表明异步开挖能够有效减小地层位移变形。

3.2 单个隧道开挖位移特征

模拟分析时，每次开挖2m，开挖总长=2×开挖次数n，左线隧道开挖至各工况设定的超前距离后停止开挖，再进行右线隧道开挖。得到左线隧道单独开挖时沿开挖长度上各个截面拱顶点A竖直位移、拱腰点D水平位移量变化情况，如图3所示。

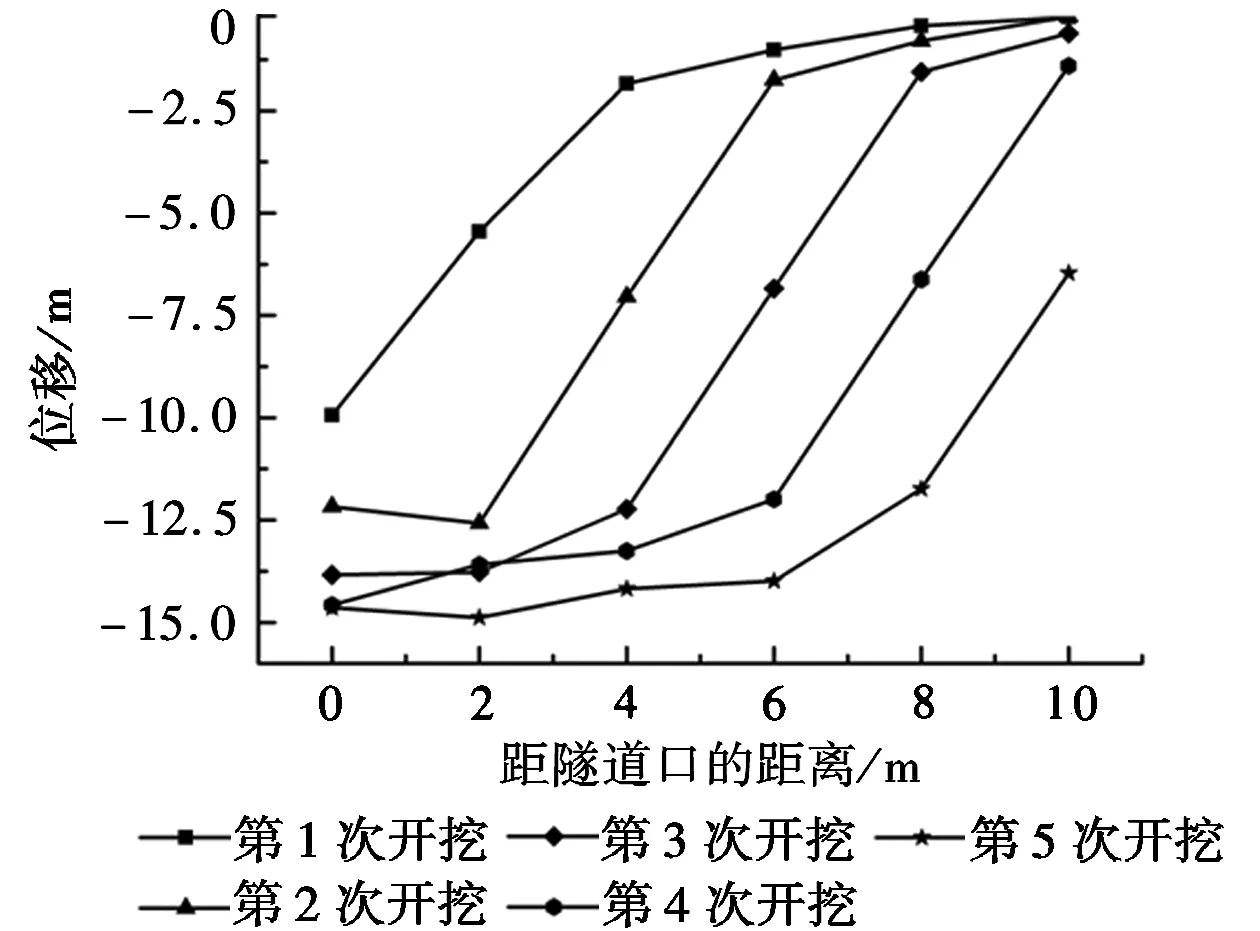
(a)左线隧道拱顶竖直位移量

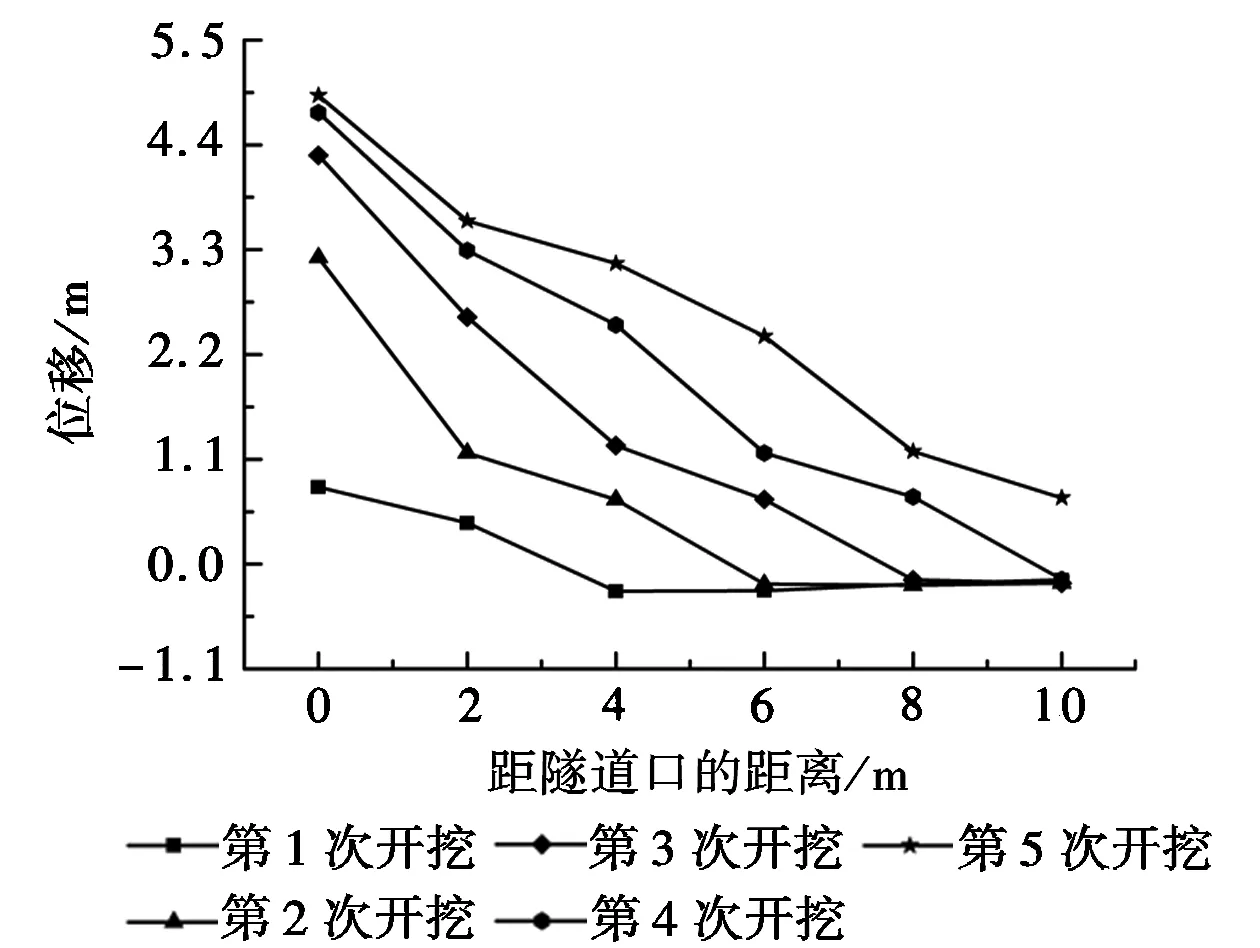
(b)左线隧道拱腰水平位移量图3 左线隧道开挖的位移特征

由图3(a)可知，当第一次开挖时，位移最大值在洞口，为14mm；随着隧道开挖次数的增加，每次开挖所产生的位移变形量越小，所有监测点的位移最后都趋于一个稳定值；开挖时，除了对已开挖的隧道产生扰动外，对开挖面前方4m范围内也产生了影响，拱顶也出现下沉，施工时要控制一次开挖距离，避免因距离过大引起冒顶。

由图3(b)可知，左线隧道的拱腰水平位移与图3(a)的拱顶竖直位移，具有相同的变化规律。说明每2m前进开挖，在沿隧道开挖方向上的开挖前4m左右范围内的位移变化有影响。

3.3 不同超前距离时隧道拱顶位移变化

模拟时左线隧道先行开挖、右线隧道后开挖，施工过程对左线隧道影响更大，故仅对左线隧道各监测点位移量进行分析。图4为不同工况时左线隧道拱顶点的位移量与开挖距离关系；超前间距50m、40m、30m变化趋势一致，限于篇幅未予列出。

由图4(a)可知，当两隧道同时开挖时相对于左线隧道单独开挖，拱顶位移量整体变化趋势一致。当净距大于9m时各个监测点拱顶竖直位移相差很小，说明净距大于9m时右线隧道开挖对左线隧道的拱顶竖直位移影响很小，而小于此值时开挖施工应更谨慎。

图4(b)为当超前间距在10m时各点的拱顶位移量变化情况，左线隧道的拱顶变形量先增大后减小，随着开挖的进行位移量越小，且与净距大小关系不密切。

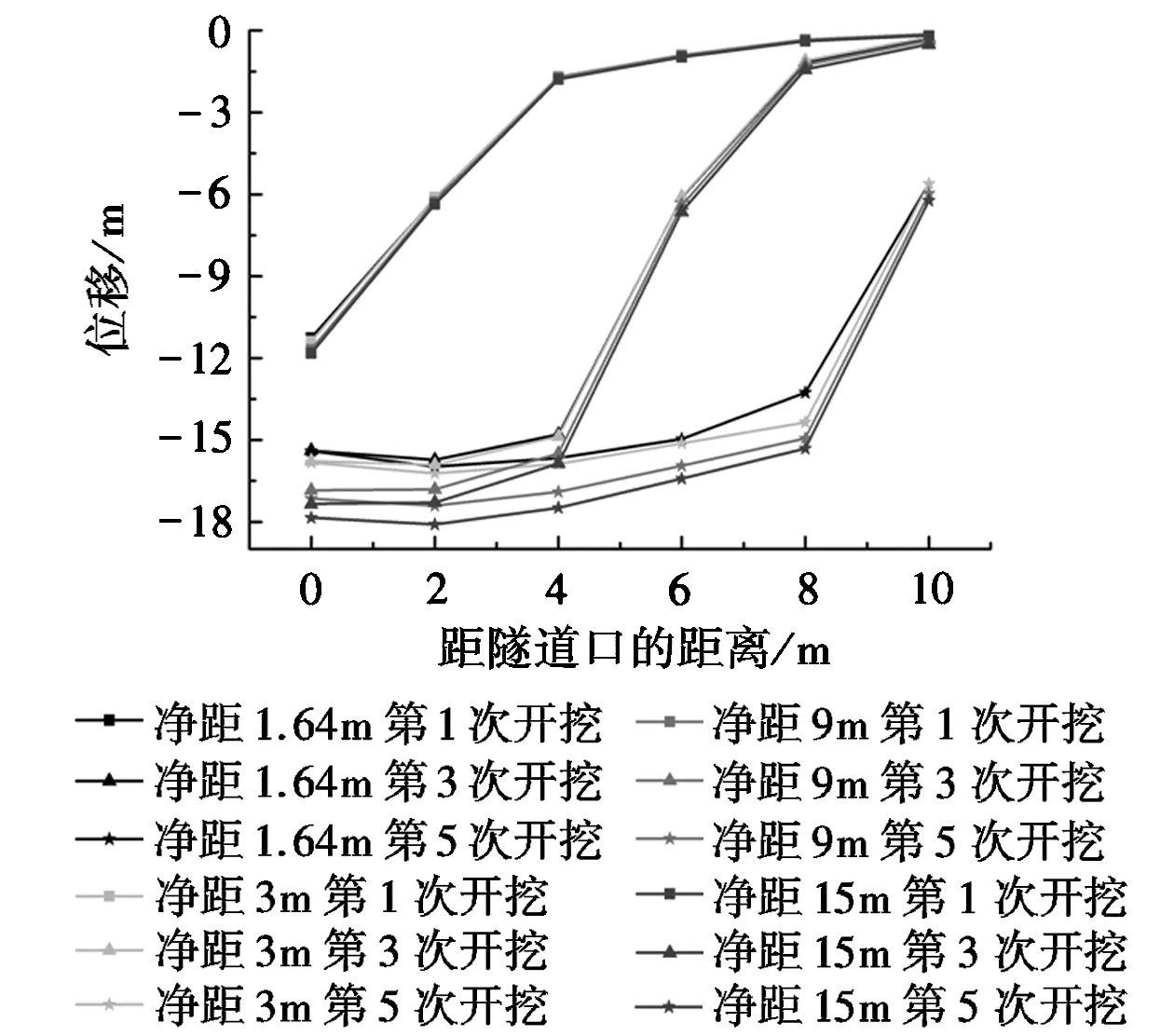
(a)超前0m时左线隧道拱顶位移变化

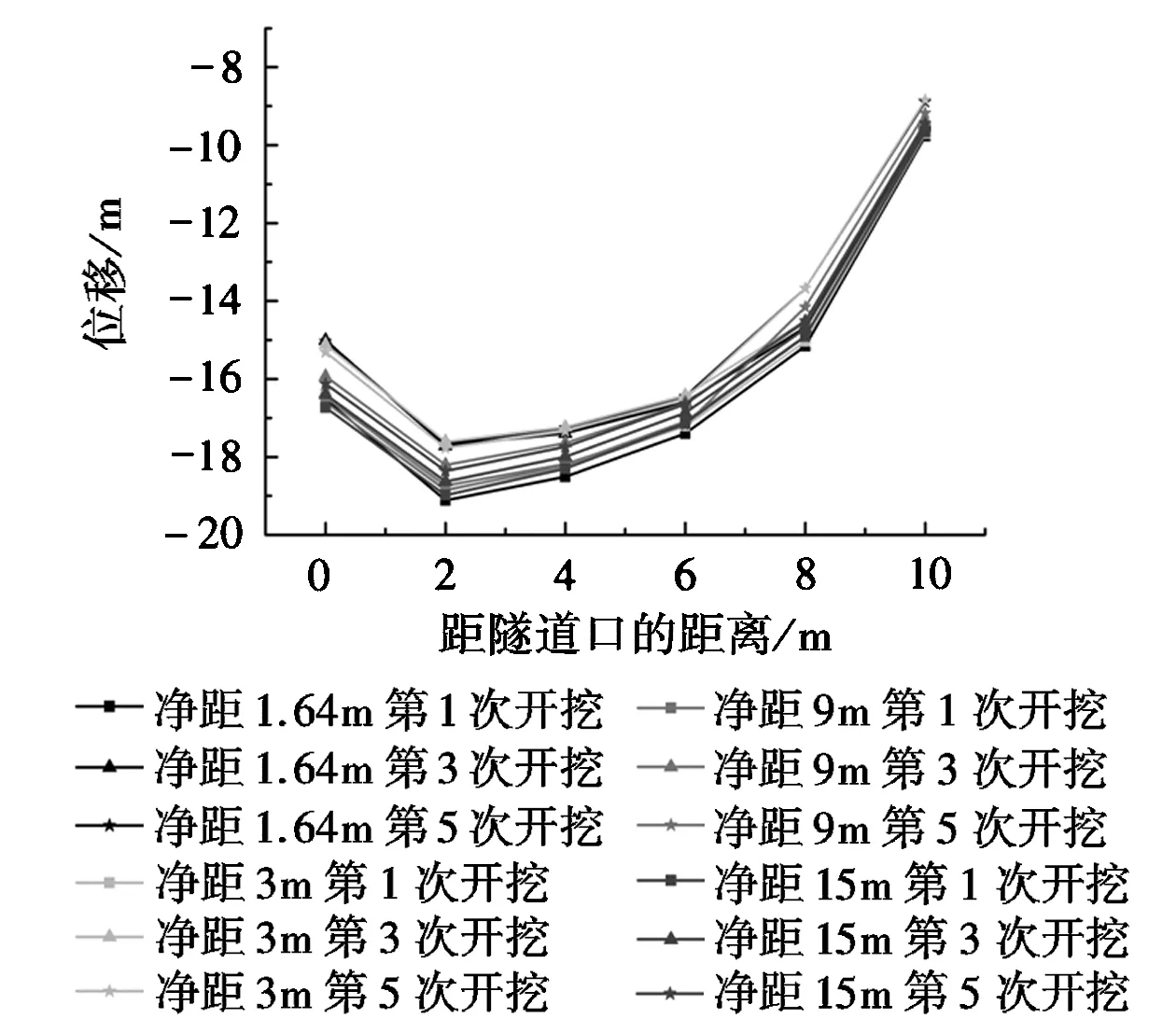
(b)超前10m时左线隧道拱顶位移变化

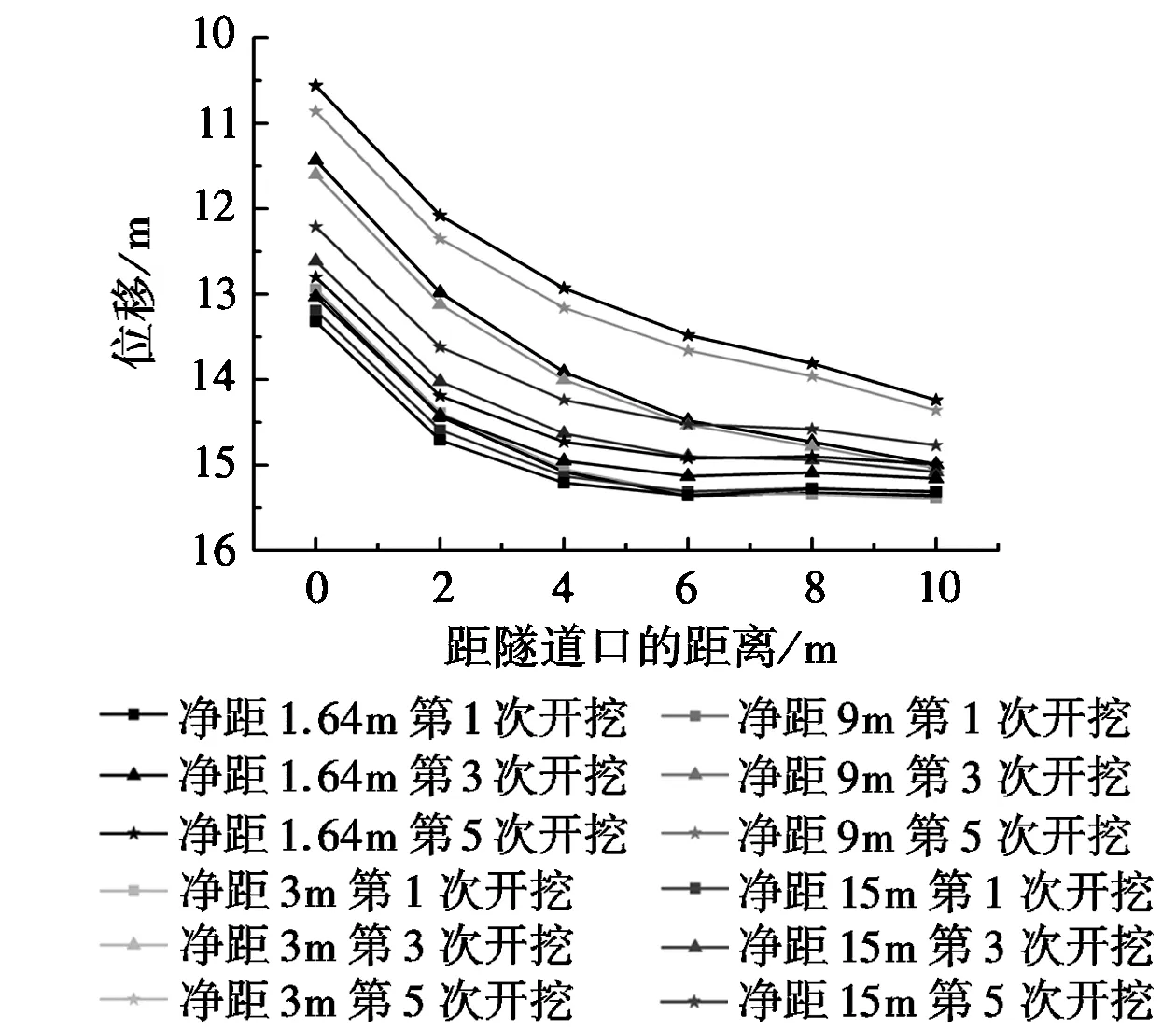
(c)超前20m时左线隧道拱顶位移变化图4 左线隧道拱顶位移变化

图4与图3相比较，对于同一个截面，当净距相同时，随着超前距离增大左隧道超前开挖的位移量减小；当右隧道继续开挖时，不同超前距离的左隧道位移变化虽然变化趋势一样，最后稳定的位移值仍然随超前间距增大而减小。此外，隧道拱顶竖直位移受超前距离变化的影响大于净距变化的影响。

3.4 不同超前距离时隧道拱腰位移变化

超前0m、10m、20m，净距1.64m、3m、9m、15m时隧道拱腰位移变化如图5所示。

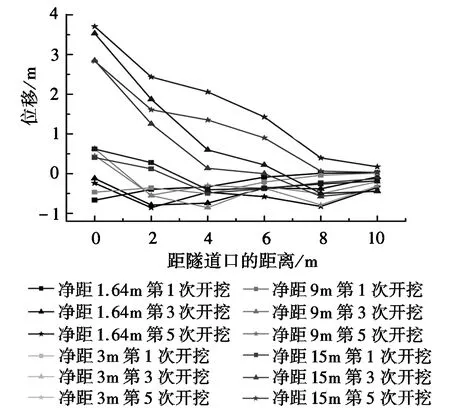
(a)超前距离0m左线隧道拱腰水平位移

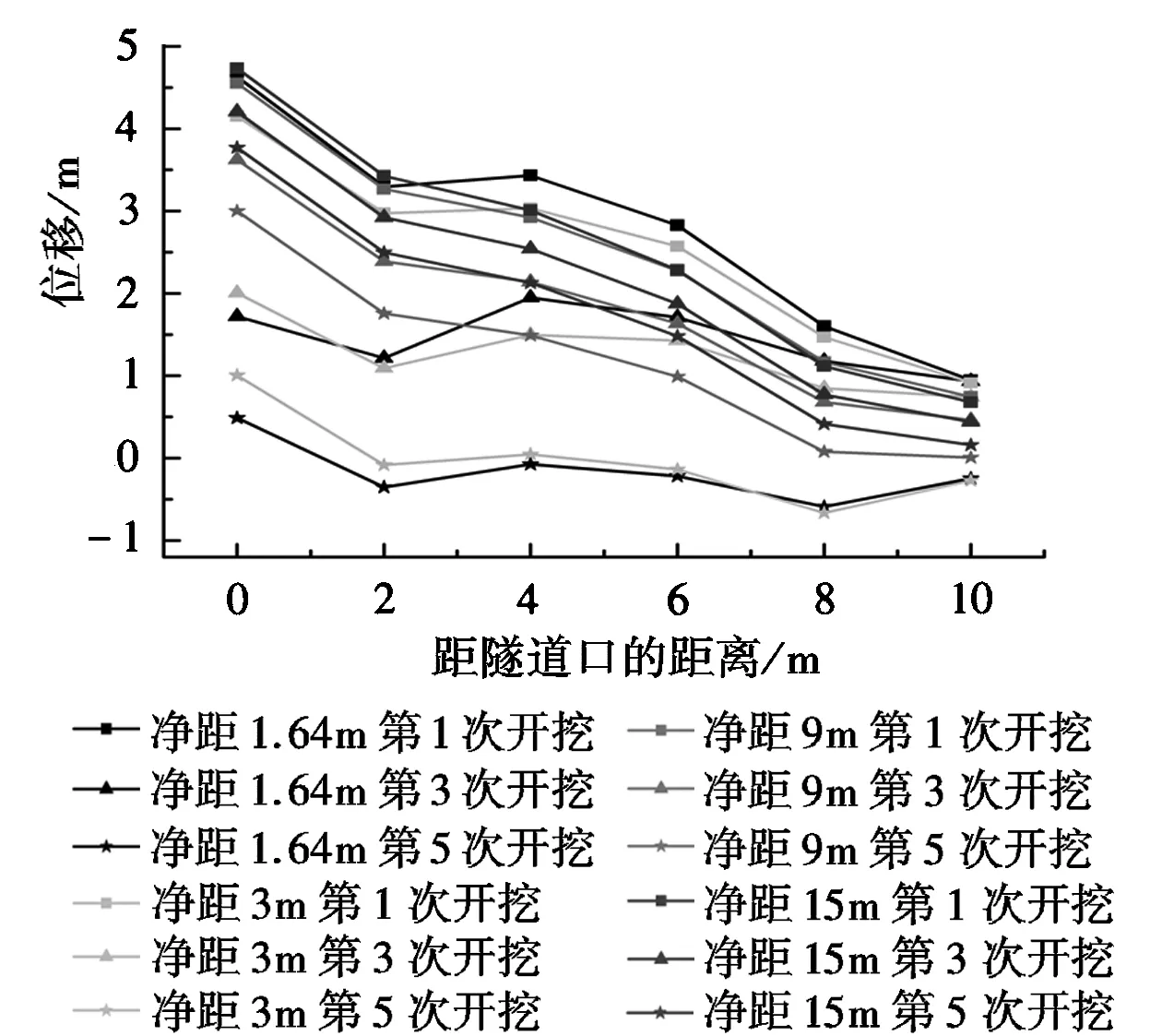
(b)超前距离10m左线隧道拱腰水平位移

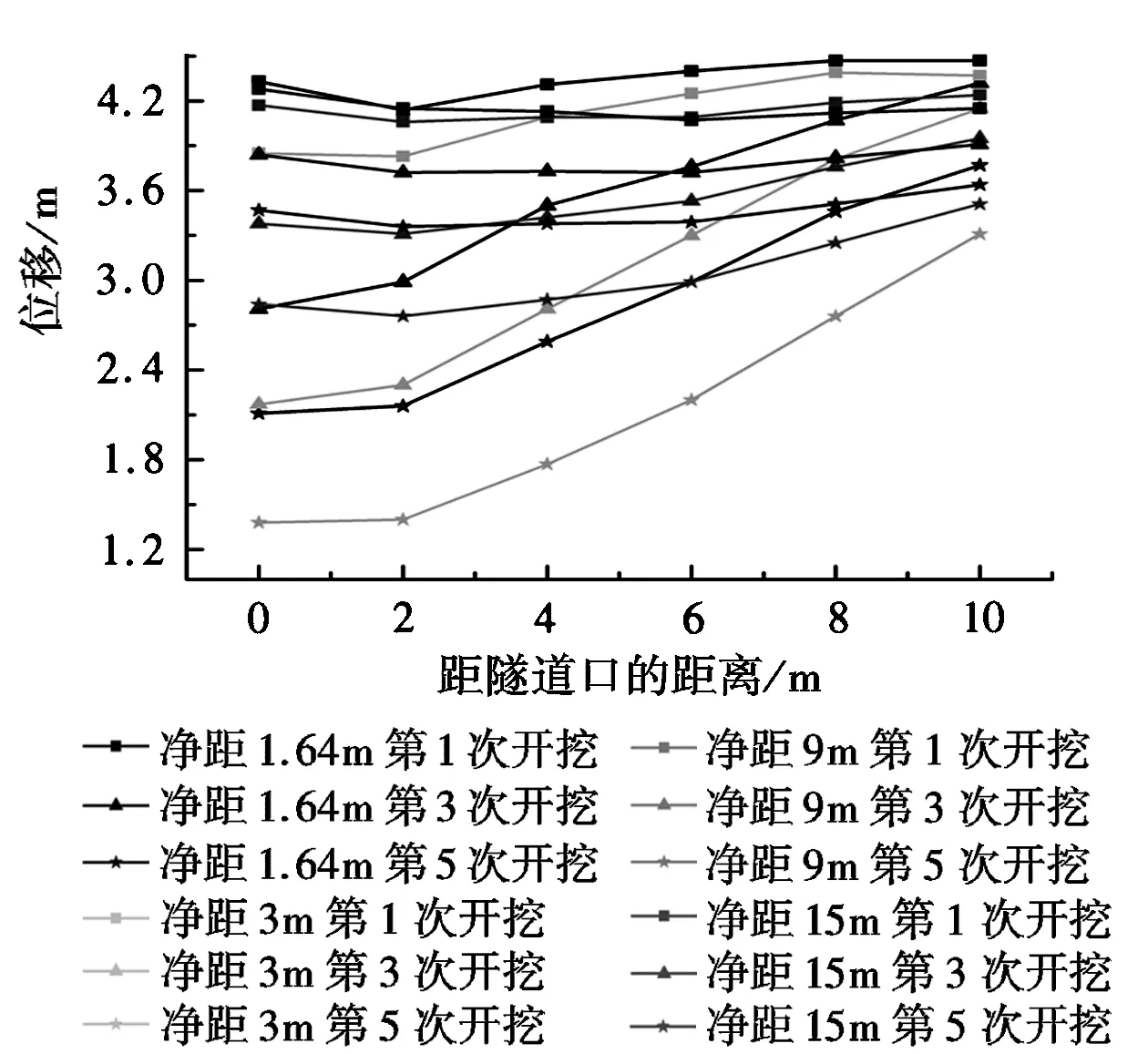
(c)超前距离20m左线隧道拱腰水平位移图5 左线隧道拱腰水平位移

由图5可得，各净距和超前距离时，隧道拱腰水平位移均在5mm以内；且至开挖面距离越小，变形量越小。图5(a)中净距小于9m时，隧道拱腰位移出现负值，表明隧道围岩向内收缩。其他工况下，隧道拱腰位移均为正值，说明左线隧道受右线隧道施工影响和上覆岩土层自重作用，隧道拱腰向右线方向变形，即向外扩张。对比图5和图3(b)，对于同一个截面、净距时，随着超前距离增大左线隧道超前开挖的稳定位移量减小；当右线隧道继续开挖时，不同超前距离的左线隧道位移虽然变化趋势一样，最后稳定的位移值仍然随超前间距增大而减小。

3.5 不同超前距离时隧道拱顶地表位移变化量

表2和表3分别表示超前20m、50m时，右线隧道开挖时左线隧道地表位移的增加量。

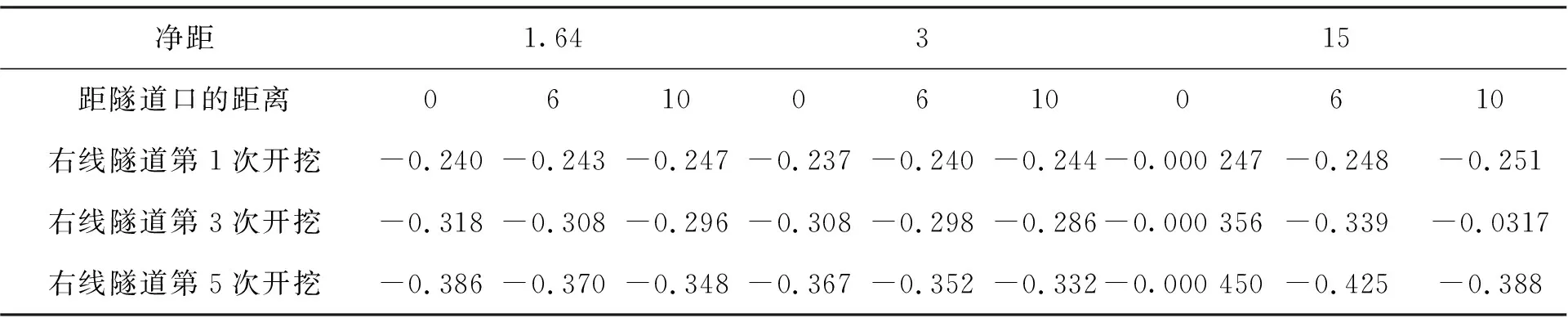
表3 超前50m左线隧道地表沉降增加量 m

由表2、表3可知，右线隧道开挖增大了左线隧道地表沉降，但是不论净距多少，地表沉降变化量相差不大。对于超前20m时，地表沉降量为正值，表明由于模型体中轴线处沉降值较大，隧道上方土体受到向中轴线方向挤压，造成地表向上隆起。

4 现场监测

4.1 实测数据

实际施工时，每10～15m布置一个断面进行拱顶位移、 地层沉降监测，监测频率为每1～2d1次。由于篇幅限制，仅列出左线开挖时DK45+878(距隧道口0m)和DK45+888(距隧道口10m)断面30d的拱顶位移、地层沉降曲线如图6所示。

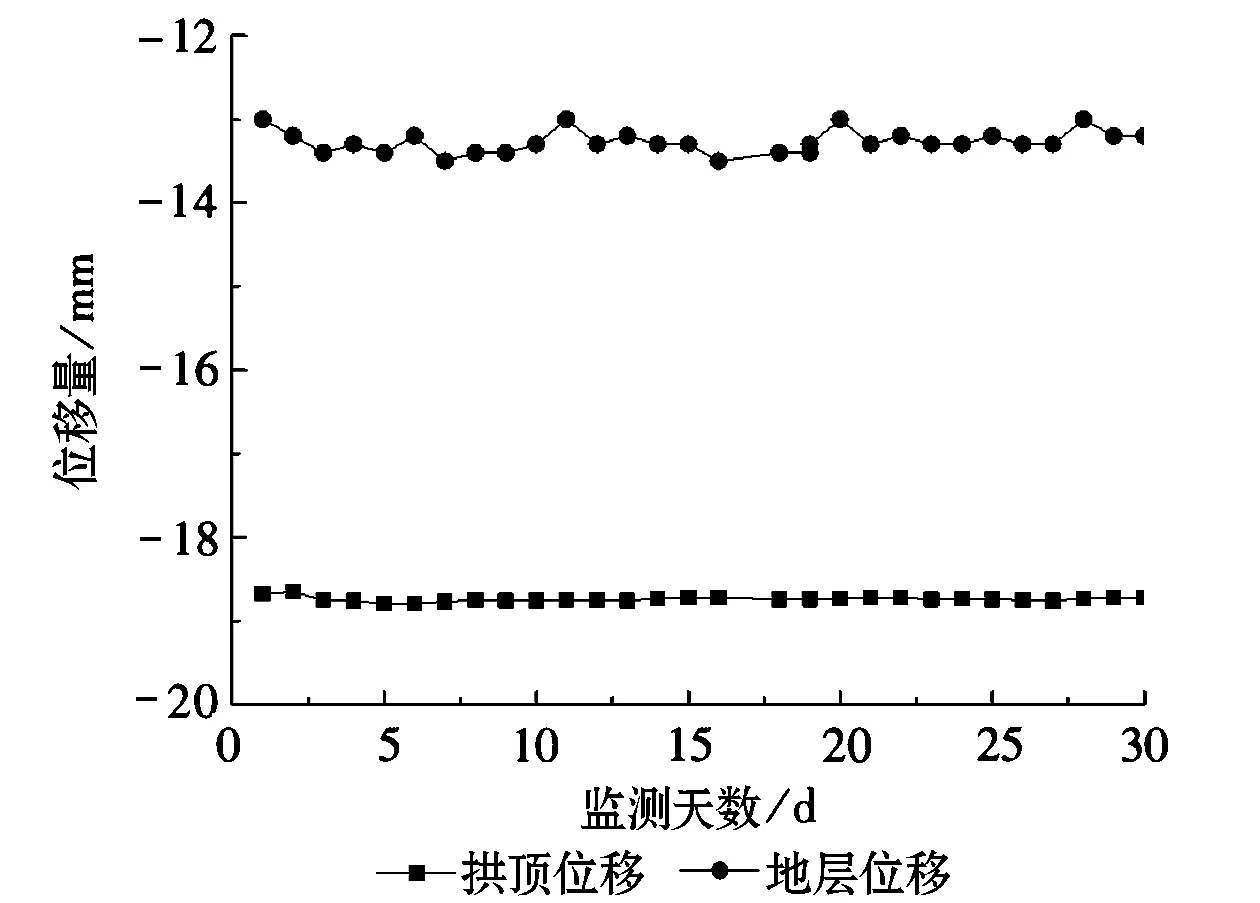
(a)DK45+878断面监测点位移

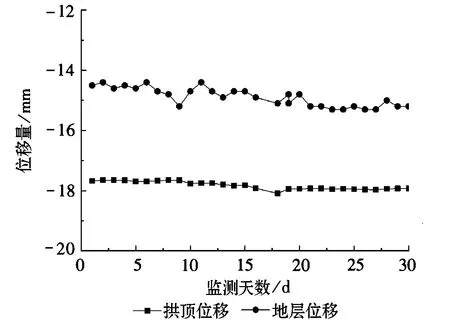
(b)DK45+888断面监测点位移图6 典型监测点位移

根据施工场地周围环境，确定隧道变形的警戒值为24mm、控制值为30mm。由图6所示，隧道开挖后拱顶和地表位移较为稳定，没有出现较大幅度的增长，均在警戒值范围内；且地表较拱顶位移量大，表明在超前支护作用下，隧道顶部具有较好的支撑作用。

4.2 实测数据对比分析

实际施工时左线隧道超前距离保持在20m以上，图7为左线隧道超前20m不同开挖天数时图4(c)监测点1(距隧道口0m处)和监测点2(距隧道口10m处)的拱顶位移与实际监测结果柱状对比。图3与图6的地层位移相比，数值模拟结果与实际监测结果相差1～2mm，均在警戒值允许范围内。表明模拟结果是可靠的，可以为施工方案与工序优化提供参考。

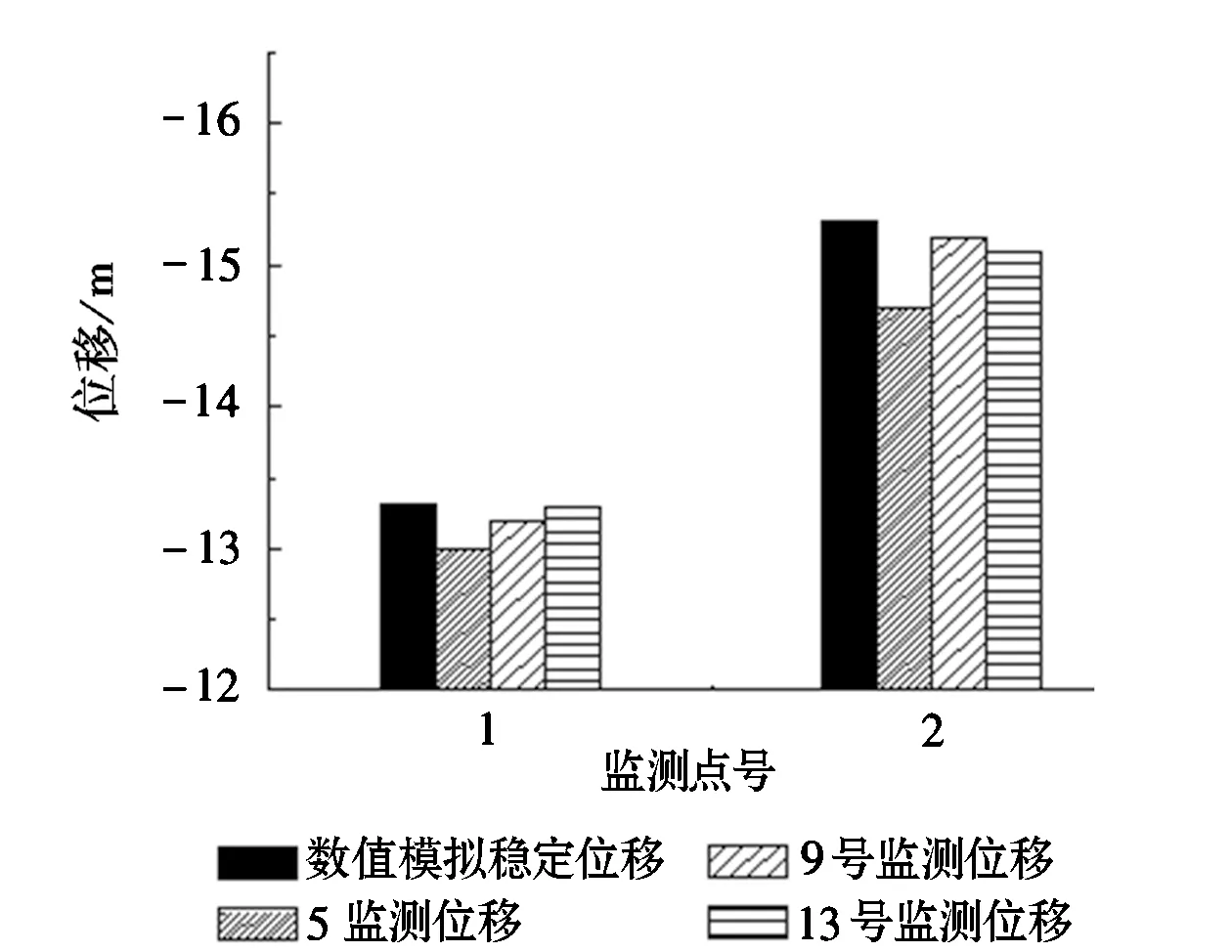
图7 监测结果与模拟结果对比

5 结论

对于覆盖层为黏土和中风化石灰岩、且隧道上覆石灰岩厚度较薄条件下，净距相同、超前间距大于10m时，先后开挖隧道的位移可以控制在安全范围内。

当超前距离相同，净距大于9m时，后开挖隧道对先开挖隧道的水平和竖向位移的影响较小，且净距越大位移变化率越小。

适当的超前距离可以减小地层位移和隧道的变形，超前距离越大最终位移越小。当两隧道间净距小于9m时应该做好中隔岩墙的加固和支护，避免先开挖隧道向内收缩过大。