边缘效应对微型振动式驻极体发电机输出功率的影响

杨胜齐，丁 梦, 2，黄樟钦, 2，王晓懿, 2



边缘效应对微型振动式驻极体发电机输出功率的影响

杨胜齐1，丁 梦1, 2，黄樟钦1, 2，王晓懿1, 2

(1. 北京工业大学北京未来网络科技高精尖创新中心，北京 100124；2. 北京工业大学北京市物联网软件与系统工程技术研究中心，北京 100124)

本文主要介绍了微型自供电系统中的一种类型——驻极体发电机的工作原理，针对微型发电机的特点，引入了边缘效应，验证了驻极体发电装置的理论输出功率模型，分析验证了微型电容在考虑边缘效应情况下的实际输出功率，根据实际输出功率模拟得出理论模型，从而得出在考虑边缘效应的情况下，微型自供电驻极体发电装置的输出功率模型．并且将BJ模型与FE-BJ模型进行对比，通过MATLAB仿真软件得出忽略边缘效应时，平板电容的宽度与间距比小于28.724时，FE-BJ模型的输出功率误差在10%,以内，此时可用FE-BJ模型来模拟计算微型驻极体发电装置的输出功率．

自供电系统；功率输出模型；边缘效应；最佳模型

无线传感器网络已经被广泛应用于各种领域，如医疗护理、环境监测、军事领域、交通领域、目标监控等[1]．而影响无线传感器网络性能和生命周期的关键因素是节点的能量供给．通过WSN(wireless sensor networks)数据融合算法可以降低节点能量消耗从而延长其工作周期[2]．虽然降低能耗可以延长无线传感器网络节点的使用时间，但是无法从根本上解决其能量消耗殆尽的问题．为了解决这一问题，需要研究从周围自然环境中收集存储能量，并通过高效存储和节约能源、降低消耗等方法，实现无线电传感器节点的自供电技术，从而有效地延长无线传感器网络的工作周期[3]．

目前对于自供电发电方式的研究主要包括3个方面：电磁发电、压电发电和静电发电[4]．而这3种发电方式都可以将周围环境的动能转化为电能[5-7].电磁发电机的原理是闭合电路的部分导体在磁场中切割磁感线运动，从而使导体产生电流[8]．但是作为微型发电装置，这种方式所产生的电压值小，必须增加线圈或增大磁场来增加其电压值，这两种方式都会受到芯片尺寸的限制[9]．压电发电机的原理是利用压电材料的压电效应，当外力作用在材料表面时，表面会形成电势差，运用电能收集装置，将其电量收集，从而将动能转化为电能[10-11]．压电材料可以用来建造道路，通过车辆在道路上对压电材料所施加的压力，将动能转化为电能[12-13]，但是其串联阻抗较大．静电发电机是利用感应生电、尖端放电或摩擦生电的方式产生高电压的一种静电装置．利用静电发电作为原理的摩擦起电的纳米发电机(triboelectric nanogenerator，TENGs)已经实现[14-15]．从材料和结构上看，前两种发电方式都无法用微加工工艺来实现，而微型静电式发电装置可以通过改变其微型可变电容来实现．驻极体微型发电装置由于其能够在周围低频振动的情况下产生较大输出功率的特点，该研究方向成为近年来静电式发电装置的研究热点[16-18].本文主要以驻极体发电装置为研究对象，分析发电装置中的能量转换模型，通过研究其边缘效应在微型发电装置中的影响，从而提出一种更加接近实际发电转换率的模型．

自从Jefimenko发明了第1个驻极体发电机以来，许多基于驻极体的静电发电装置就被广泛研究．目前关于驻极体静电发电机振动能量采集装置的力学模型分析已经形成了一个激烈的研究领域.其中，Sterken等[19]提出了一种发电模型，该模型的上极板与一个振动质量块相连接，质量块通过弹簧和一个阻尼装置相连接，该阻尼装置保证了移动质量块在一定的范围内移动，下极板固定在整个振动收集装置中，在外界发生振动时上极板与下极板产生相对位移，从而形成电流．Lo等[20]设计了一种梳状电机型发电机．该发电机由上下两块玻璃组成，下方玻璃上固定有呈梳妆交叉的电极，在玻璃上方有一层驻极体材料，上方玻璃有两条金属电极，当上方玻璃由于外界环境发生水平振动时，上方金属电极与所对应的驻极体产生相同的电荷，即图形化驻极体发生水平振动，从而形成电流．Naruse等[21]提出了一种转动式发电结构．该发电机结构中，衬底材料为玻璃，将深槽用激光的方法刻蚀，再将微型小球放置于深槽内，通过控制槽内的深度来调节金属电极与驻极体的间距，从而形成电流．除了上述力学模型外，驻极体发电装置还包括了能量转化模型，当外界发生振动时，上下极板的正对面积发生变化，从而产生电流．根据最新的研究成果，Nguyen等[22]研究了一般正弦激励下微型驻极体发电机的分析模型，近期学者们还研制出了一种高开路电压的独立式驻极体发电机，这种发电机模型是为了解决微型驻极体发电机在运行过程中摩擦所产生的能量消耗[23]．学者们还研究了一种DEG模式的混合驻极体-介电弹性体发生器．在该构造中，驻极体材料被用作经典DEG的偏振源，即基于电容变化的静电发生器，提高了发电机的输出功率[24]．但是这些模型只针对能量消耗、正弦振动的问题，对于边缘效应并没有做出说明．对于微型发电系统中的边缘效应对发电输出功率的影响，也有一些学者做了相应的研究，李勇等[25]研究了非平行梳状驱动器中的边缘效应对静电力的影响，运用有限元法的仿真模型验证了考虑边缘效应的梳状驱动器的静电力计算模型更为准确．学者针对具有槽孔的微型梳状电容器的边缘效应进行了研究[26]，得出在宽度和厚度固定时，长度越小的电容的边缘效应越大．学者还针对边缘效应提出了一种减小边缘效应对测量精度影响的方法[27]．但是以上对于边缘效应的研究只是针对梳状电容器，并没有针对边缘效应对微型发电机输出功率的影响做出相应的研究．本文研究边缘效应对微型振动式驻极体发电机输出功率的影响，并且得出在考虑边缘效应情况下的输出功率模型．

1 静电转换模型

为了优化静电转化模型，必须建立一个准确的驻极体发电输出功率的数学模型．

BJ(Boland Justin)模型电能输出功率为

 (1)

式中：为驻极体发电机的振动频率；为驻极体表面电荷密度；为转子的半径；为上极板与驻极体的距离；为驻极体的厚度；tret为驻极体的介电常数；0为上、下极板间介质的介电常数；为常数．

证 明 驻极体发电机的模型如图1所示．

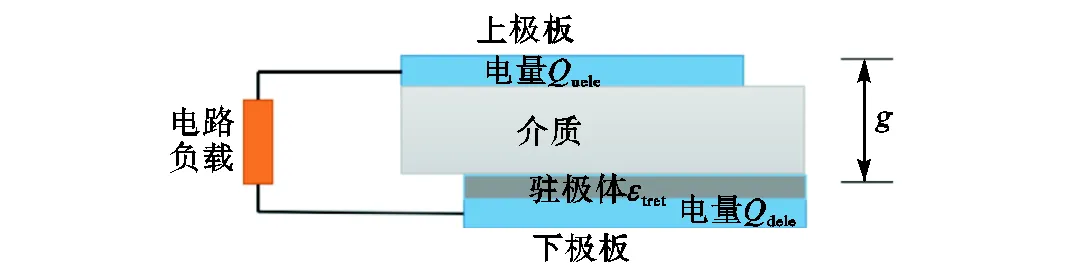
图1 驻极体发电装置能量转换模型

假设上极板与下极板之间的介质为真空，下极板上为驻极体tret，上极板的电量为uele，下极板的电量为dele，上极板与驻极体的距离为，驻极体的厚度为，由静电感应现象可知

 Qtot＝Quele＋Qdele(2)

当周围环境发生振动时，上极板与下极板的正对面积会随时间发生变化，此时其模型中的上、下电容分别为

 Cuele＝(3)

 Cdele＝(4)

而其模型中的电压为

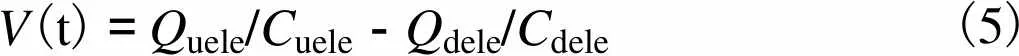
 V(t)＝Quele/Cuele－Qdele/Cdele(5)

可知

 (6)

由欧姆定理和积分并且结合式(6)可知

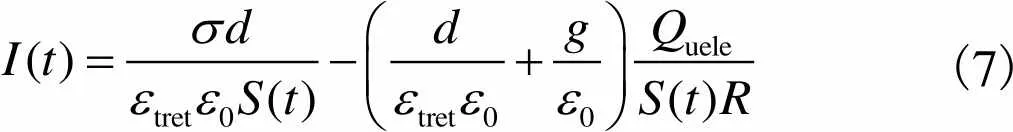
 (7)

在外界发生振动时，极板正对面积的长度会发生变化，由振动规律和面积计算公式可得

 (8)

 (9)

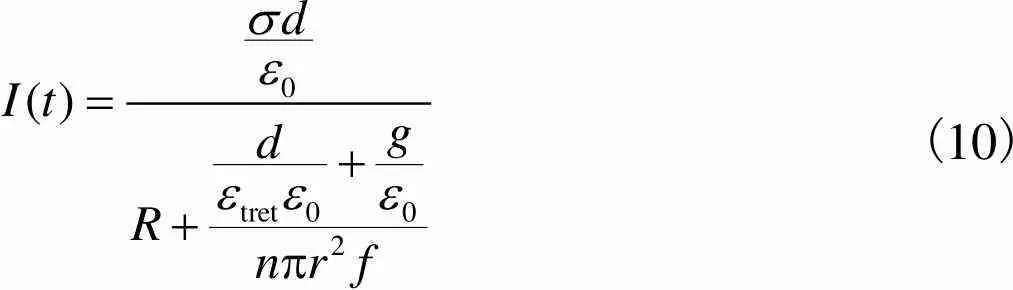
 (10)

由式(10)可知，在＝0电路负载为

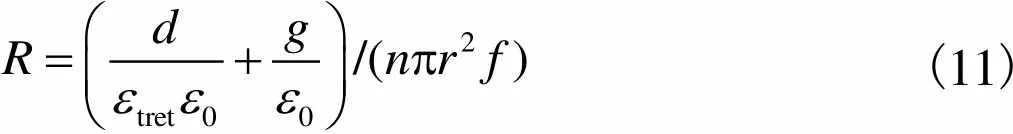
 (11)

根据功率计算公式可知其输出功率最大值为式(1)所示的值．

以上BJ模型是在忽略了边缘效应情况下得出的模型，而用Ansoft Maxwell对平板电容进行建模仿真，结果如图2所示，结合图片的数据可知在平板电容的边缘的能量是不均匀的，存在边缘效应，在MEMS中，边缘效应会影响电路的测量级度，对整个电路模型的影响是不可忽视的．

图2 平板电容能量分布

在考虑边缘效应的影响下，假设有一平板电容器宽度为2，上下极板的间距为2，其中上下极板的长度无限延伸，由于平板电容的对称性的特点，为了便于计算，可以将平板电容的1/2作为研究对象，将其三维模型利用施瓦茨-克里斯托费尔映射到二维坐标系中，如图3所示．其中′、′、′、′分别映射到、、、，所用的变换为

   (12)

图3 二维坐标映射

将上述公式用第1类椭圆积分与第2类椭圆积分表示，可得

 (13)

将(，1)、(，1/1)、(，1/)分别代入用第1类椭圆积分和第2类椭圆积分表示的式(13)中得

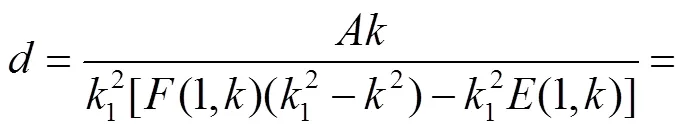
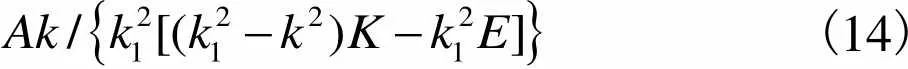
   (14)

第1类完全椭圆积分表示为

 K＝F(1，k)(15)

第2类完全椭圆积分表示为

 E＝E(1，k)(16)

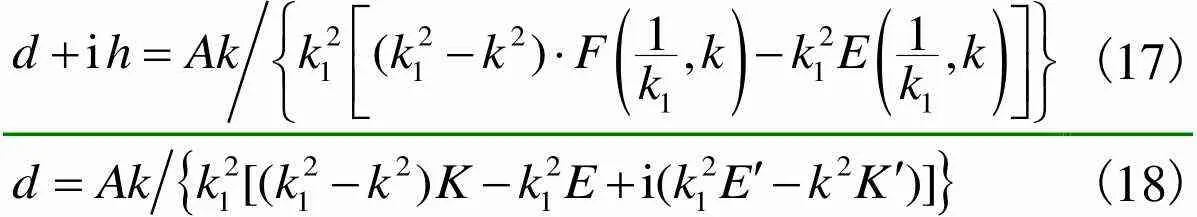
 (17)      (18)

其中所表示的中间值分别为

 F(1/k，k)＝K＋K′(19)

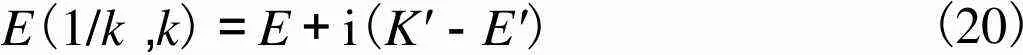
 E(1/k，k)＝E＋i(K′－E′)(20)

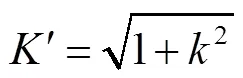
 (21)

由勒让德多项式知

 EK′＋E′K－KK′＝(22)

将式(21)与式(14)结合可得

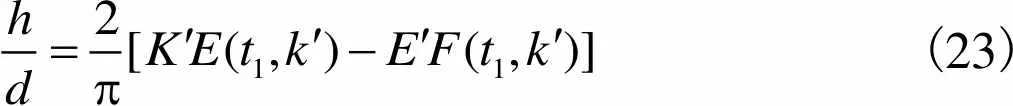
 (23)

利用施瓦茨-克里斯托费尔映射将其变化为图3中的矩形1,1,1′1′，此时运用的公式为

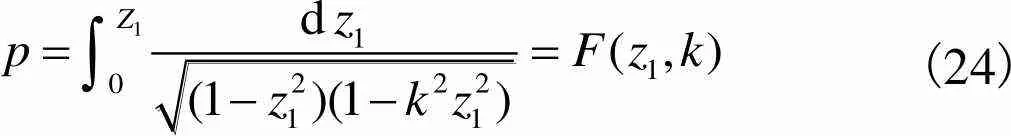
 (24)

将平面上对应的点代入式(23)中，可得点的坐标为－＋i，点的坐标为＋i．经过施瓦茨-克里斯托费尔映射，将平面的电场变为平面内的矩形．所以在平面内平板电容是没有边缘效应的，上下极板的距离为2,，极板宽度为2,，得出平行板电容器单位长度的电容为

 (25)

由式(25)和不考虑边缘效应的电容公式可知，在极板的宽度和距离的比大于16.64时，电容的一般计算公式的误差可忽略不计．

上述即为考虑边缘效应的情况下平板电容器的实际电容值．将式(25)与BJ模型中公式相结合，有

 Cdele＝(26)

 Cuele＝(27)

可得

 Cdele＝(28)

 Cuele＝(29)

其模型中的电压为

 V(t)＝Quele/Cuele－Qdele/Cdele(30)

式(6)就变为

   (31)

将式(25)与上述式(7)、式(9)、式(10)结合，可最终推导出在考虑边缘效应的情况下，FE-BJ(fringe effects-Boland Justin)模型的输出功率为

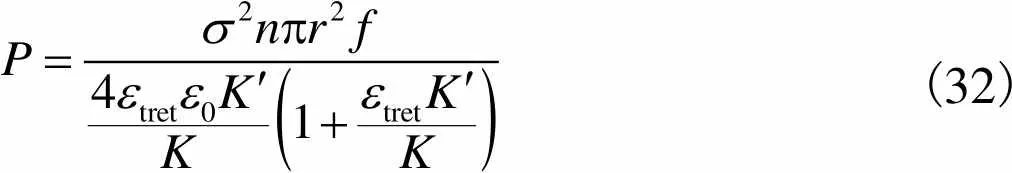
 (32)

2 参数设置与仿真分析

为了比较本文提出的FE-BJ和BJ模型与实际输出模型的误差，第2节对公式进行仿真分析．

首先设置该微型驻极体发电模型的实验数据如表1所示[4]．

理论输出功率的BJ模型可以表述为

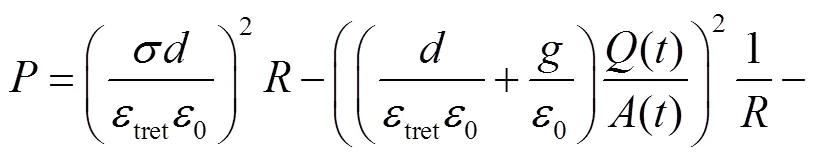
   (33)

表1 微型驻极体发电模型参数

Tab.1 Micro electret power generation model parameters

弹簧的振动频率f/Hz驻极体的厚度d/mm上下极板间介质的介电常数转子的半径r/mmTeflon驻极体的介电常数极板宽度h/mm两个极板间的距离g/mm驻极体表面电荷密度/(μC·m-2) 20151.000,5854211001.346,

将式(33)与表1所示的参数用MATLAB语言编程并运行仿真，其结果如图4所示，横坐标为时间，纵坐标为输出功率．由图4所示的周期函数可见在外界环境发生振动时，其理论输出功率随着时间的变化规律．将一个周期的函数作为研究对象，选取其中的数据作为研究对象，将BJ模型下的输出功率模型式(33)与实际的输出功率进行比较可得如图5所示的结果．

图4 BJ输出功率模型

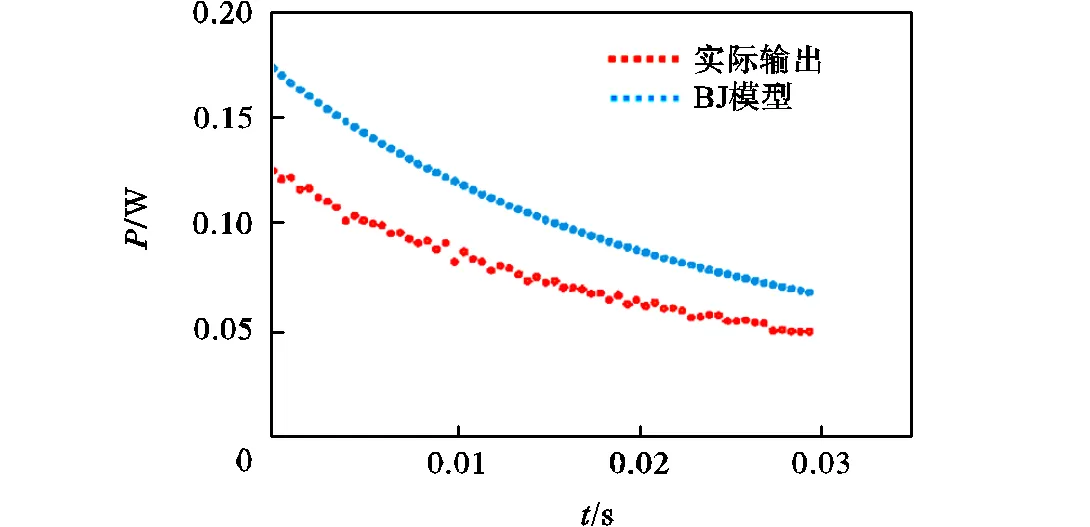
图5 BJ模型与实际输出功率比较

图5表示当外界发生振动时，随着时间的变化实际输出功率与理论输出功率的值，图中蓝色表示理论输出功率BJ模型的变化值，橙色表示实际输出功率的变化值，可知实际输出模型与理论功率输出模型BJ模型的比约为0.71．将实际功率输出值与式(33)进行比较，结果如图6所示．该图表示不同时刻实际功率的输出值与不考虑边缘效应下的BJ模型的输出功率的比值/．由图可知其比值在0.65～0.70之间波动．

在平板电容的宽度与距离的比值为10时，其FE-BJ模型中的输出功率0与BJ模型的理论输出功率之比0/为0.723,4，为了计算误差值，将图6中不同时刻/的比值与FE-BJ的输出功率0与BJ模型的输出功率比值0/做差，其结果如图7所示.

图6 实际输出模型与BJ模型的比值

图7 P/P′与P0/P′的差值

图7表示在不同时刻/′与0/的差值，由图7可知/与0/的差值在-0.04～0.03之间波动，可知其相应的实际比值与理论比值在±1.5%,之间波动，所以在考虑边缘效应的情况下的FE-BJ模型与实际情况是相吻合的．在考虑边缘效应的影响时，实际的输出功率可以用FE-BJ模型进行计算，而在平板电容的宽度与距离的比值为10时，其FE-BJ模型输出功率与BJ模型理论输出功率之比/0为0.723,4，误差为38.24%,．在以下实验中将研究当其FE-BJ模型与不考虑边缘效应的模型误差为10%,以内时，其平板电容的宽度与距离的比值．

设置该驻极体发电模型的参数如表2所示．

表2 驻极体发电模型参数

Tab.2 Electret power generation model parameters

对表2的数据进行仿真比较，结果如图8所示.图8表示在外界发生振动时，随着时间的变化BJ模型中的输出功率与FE-BJ模型中的输出功率的变化情况．由上述仿真结果可知，在极板宽度为1,664,μm时，实际输出功率与理论输出功率的比值/0＝0.874,9，误差为14.3%,．

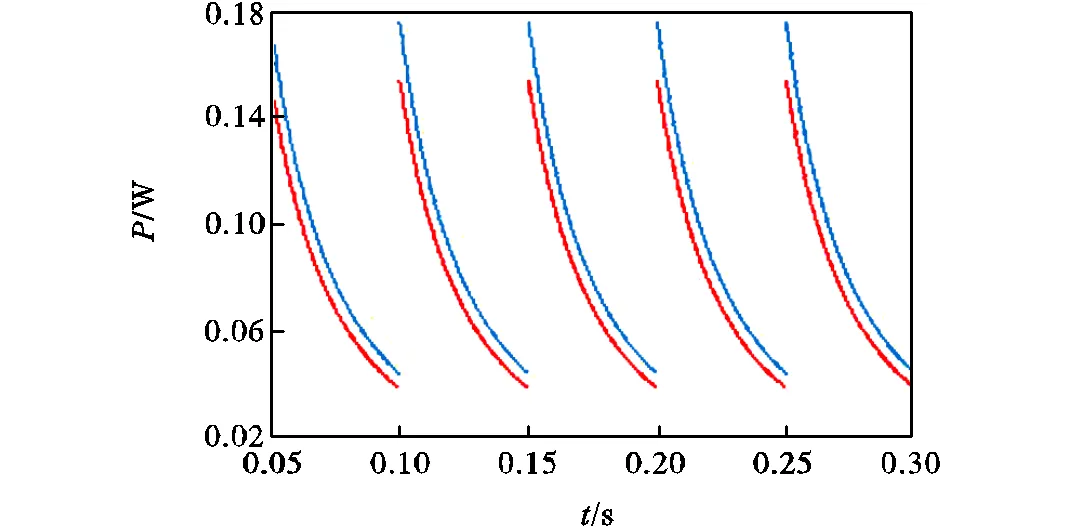
图8 BJ模型与FE-BJ模型的仿真

由上述模型可以得出在平板电容的宽度与距离之比/和FE-BJ模型中的输出功率0与BJ模型中的输出功率′之比0/′的关系，如图9所示．

图9 h/g与P0/P′的关系

图9表示随着平板电容的宽度与距离之比/的变化，其FE-BJ模型的输出功率0与BJ模型的输出功率的比值0/的变化情况，由图9可知，在/为28.724时，0/的值为0.901,5，误差为10.92%，此时FE-BJ模型的输出功率0与BJ模型的输出功率的值接近，此时的边缘效应可以忽略，可用BJ模型进行相似计算，当/的比值小于28.724时，此时计算驻极体发电机的最佳输出功率用FE-BJ的最佳模型公式进行计算．

3 结 语

本文针对微型自供电系统的输出功率进行模型计算，由于微型系统中边缘效应的存在，运用传统的BJ模型对其输出功率进行计算时，计算结果大于实际值的输出功率．而本文提出的FE-BJ模型，运用保角变换的方法对实际微型发电系统进行计算可知，其结果与实际输出功率基本吻合；并且计算出了在平板电容的宽度与距离的比值为28.724时，微型供电系统的边缘效应可以忽略，此时可以用BJ模型来进行计算，而在平板电容的宽度与距离的比值小于该临界值时，应用本文提出的FE-BJ模型对其输出功率进行计算．

［1］ Sohraby K，Minoli D，Znati T. Applications of wireless sensor networks[J]. Lecture Notes in Engineering & Computer Science，2007，2166(1)：4-5.

［2］ 徐晓斌，张光卫，孙其博，等. 一种误差可控传输均衡的WSN数据融合算法[J]. 电子学报，2014，42(6)：1205-1209.

Xu Xiaobin，Zhang Guangwei，Sun Qibo，et al. A WSN data fusion algorithm with erroneous controllable transmission equalization[J]. Journal of Electronics，2014，42(6)：1205-1209(in Chinese).

［3］ 朱俊杰，李美成. 无线传感器微能源自供电技术研究[J]. 可再生能源，2012，30(11)：55-60.

Zhu Junjie，Li Meicheng. Study on self-powered technology of wireless sensor micro energy[J]. Renewable Energy，2012，30(11)：55-60(in Chinese).

［4］ Tsutsumino T，Suzuki Y，Kasagi N，et al. Seismic power generator using high-performance polymer electret [C]// IEEE International Conference on Micro Electro Mechanical Systems. Istanbul，Turkey，2006：98-101.

［5］ Jeon Y B，Sood R，Jeong J H，et al. MEMS power generator with transverse mode thin film PZT[J]. Sensors & Actuators A Physical，2005，122(1)：16-22.

［6］ Saha C R，O’Donnell T，Wang N，et al. Electromagnetic generator for harvesting energy from human motion [J]. Sensors & Actuators A：Physical，2008，147(1)：248-253.

［7］ Bi M，Wang S，Wang X，et al. Freestanding-electret rotary generator at an average conversion efficiency of 56%,：Theoretical and experimental studies[J]. Nano Energy，2017，41：434-442.

［8］ Dai D，Liu J. Hip-mounted electromagnetic generator to harvest energy from human motion[J]. Frontiers in Energy，2014，8(2)：173-181.

［9］ Tashiro R，Kabei N，Katayama K，et al. Development of an electrostatic generator for a cardiac pacemaker that harnesses the ventricular wall motion[J]. Journal of Artificial Organs，2002，5(4)：239-245.

［10］ Xie J，Yang J，Hu H，et al. A piezoelectric energy harvester based on flow-induced flexural vibration of a circular cylinder[J]. Journal of Intelligent Material Systems & Structures，2012，23(2)：135-139.

［11］ Kerley R，Huang X，Dong S H. Energy harvesting from the human body and powering up implant devices [M]// KAIST Research Series. Berlin：Springer，2016：147-180.

［12］ Hofmann A，Laqua D，Husar P. Piezoelectric based energy management system for powering intelligent implants and prostheses[J]. Biomedical Engineering，2012，57(5)：263-266.

［13］ Xiong H，Wang L. Piezoelectric energy harvesting for public Roadways：On-site installation and evaluation[J]. Applied Energy，2016，174：101-107.

［14］ Zhu G，Chen J，Zhang T，et al. Radial-arrayed rotary electrification for high performance triboelectric generator[J]. Nature Communications，2014，5(3)：487-507.

［15］ Fan F R，Tian Z Q，Wang Z L. Flexible triboelectric generator[J]. Nano Energy，2012，1(2)：328-334.

［16］ Sterken T，Altena G，Fiorini P，et al. Characterisation of an electrostatic vibration harvester[J]. Computer Science，2007：297-300.

［17］ Tvedt L G W，Blystad L C J，Halvorsen E. Simulation of an electrostatic energy harvester at large amplitude narrow and wide band vibrations[C]//2008 Symposium on Design，Lest，Integration and Packaging of MEMS/ MOEMS. Nice，France，2008：296-301.

［18］ Peano F，Tambosso T. Design and optimization of a MEMS electret-based capacitive energy scavenger[J]. Journal of Microelectromechanical Systems，2005，14(3)：429-435.

［19］ Sterken T，Fiorini P，Baert K，et al. Novel design and fabrication of a MEMS electrostatic vibration scavenger [C]//Power MEMS. Kyoto，Japan，2004：18-21.

［20］ Lo H W，Whang R，Tai Y C. A simple micro electret power generator[C]//International Conference on Micro Electro Mechanical Systems. Kobe，Japan，2007：859-862.

［21］ Naruse Y，Matsubara N，Mabuchi K，et al. Electrostatic micro power generation from low-frequency vibration such as human motion[J]. Journal of Micromechanics & Microengineering，2009，19(9)：94-99.

［22］ Nguyen C，Ranasinghe D，Al-Sarawi S. Electret-based microgenerators under sinusoidal excitations：An analytical modeling[J]. Smart Structures & Systems，2018，21(3)：335-347.

［23］ Bi M，Wang S，Wang X，et al. Freestanding-electret rotary generator at an average conversion efficiency of 56%,：Theoretical and experimental studies[J]. Nano Energy，2017，41(1)：434-442.

［24］ Lagomarsini C，Jeanmistral C，Sylvestre A. New approach to improve the energy density of hybrid electret-dielectric elastomer generators[C]//Society of Photo-Optical Instrumentation Engineers(SPIE)Conference Series. Oregon，USA，2017：101632,C.

［25］ 李 勇，李玉和，李庆祥，等. 计及边缘效应的非平行梳状驱动器的静电力计算[J]. 清华大学学报：自然科学版，2003，43(8)：1024-1026.

Li Yong，Li Yuhe，Li Qingxiang，et al. Electrostatic force calculation of non-parallel comb drivers considering edge effect[J]. Journal of Tsinghua University：Science and Technology，2003，43(8)：1024-1026(in Chinese).

［26］ Dong Linxi，Huo Weihong，Yan Haixia，et al. Analysis of fringe effect of MEMS comb capacitor with slot structures[J]. Integrated Ferroelectrics，2011，129(1)：122-132.

［27］ Wang W，Wen Y，Yu J，et al. Impact of fringe effect on measuring accuracy of planar capacitive sensors[J]. Sensor Letters，2011，9(4)：1458-1461.

(责任编辑：王晓燕)

Effect of Fringe Effect on Output Power of Micro-Vibration Electret Generator

Yang Shengqi1，Ding Meng1, 2，Huang Zhangqin1, 2，Wang Xiaoyi1, 2

(1. Beijing Advanced Innovation Center for Future Internet Technology，Beijing University of Technology， Beijing 100124，China； 2. Beijing Engineering Research Center for IoT Software and Systems，Beijing University of Technology， Beijing 100124，China)

This paper mainly introduces the working principle of one type of electret generator in micro self-powered system. According to the characteristics of the micro generator，the fringe effect was introduced to verify the theoretical output power model of the electret generating device and analyze the micro capacitor in consideration of the actual output power under the condition of fringe effect. The theoretical model was simulated according to the actual output power and thus the output power model of self-powered micro electret generating device was concluded，considering the fringe effect. Boland Justin(BJ)model and fringe effects-Boland Justin(FE-BJ)model were compared and it was calculated by use of MATLAB simulation software that ignoring the fringe effect，width and spacing ratio of plate capacitor is less than 28.724 and the output power error of FE-BJ model is less than 10%. Under these circumstances FE-BJ model can simulate the output power of micro electret generating device.

self-charging system；power output model；fringe effect(FE)；optimal model

10.11784/tdxbz201711044

TM387

A

0493-2137(2019)03-0293-07

2017-11-04；

2018-07-05.

杨胜齐（1977—  ），男，博士研究生，教授，syang@bjut.edu.cn.

丁 梦，macey_ding@163. com.

国家自然科学基金资助项目(61602016).

the National Natural Science Foundation of China(No. 61602016).