基于RNA遗传操作的改进蝙蝠算法

耿艳香，张立毅，孙云山，费 腾，蒋师贤，马嘉骏



基于RNA遗传操作的改进蝙蝠算法

耿艳香1, 2，张立毅1, 2，孙云山2，费 腾2，蒋师贤2，马嘉骏2

(1. 天津大学电气自动化与信息工程学院，天津 300072；2. 天津商业大学信息工程学院，天津 300134)

蝙蝠算法作为一种新型的元启发式算法，具有优越的寻优能力和广泛的应用空间，同时也存在着收敛速度和精度的制约问题及个体之间欠缺交互等问题，针对这些不足，引入了RNA遗传算法增强个体之间的交流，通过信息的交叉和变异等变化措施，加快了算法的搜索能力，提高了搜索精度. 通过测试函数验证了改进后的算法具有较好的收敛精度、可靠性和稳定性，大大提升了蝙蝠算法的寻优能力.

蝙蝠算法；RNA遗传；交叉；变异

智能仿生算法做为新兴的智能优化算法，是解决函数优化[1]、路径搜索[2]、数据分析[3]等问题的有效手段．近年来学者们提出了多种新型智能仿生算法，典型代表有鱼群算法[4]、粒子群算法[5]、蚁群算法[6]、蜂群算法[7]，并在多个领域得到较好的应用．

2010年，剑桥大学的Yang教授[8]根据蝙蝠自身的回声定位能力，提出一种新型的智能仿生算法——蝙蝠算法．蝙蝠在飞行过程中发出不同频率的超声波，经过物体反射后，根据反馈信息调整飞行策略．盛孟龙等[9]通过对蝙蝠算法的全局收敛性分析验证，得出该算法无法确保全局收敛的结论，因此对蝙蝠算法提出有效的改进是有必要的．李雅梅等[10]运用Powell机制改进蝙蝠算法，将传统的Powell算法作为一种局部搜索算子，嵌入到蝙蝠算法中，提高蝙蝠算法的局部搜索能力．屈迟文等[11]将入侵杂草算法的生长繁殖、空间扩散和竞争机制引入蝙蝠算法，增加了蝙蝠算法的局部搜索能力．尚俊娜等[12]提出的具有自学习能力和个体变异的蝙蝠算法，弥补了算法高维弱势的缺陷．RNA遗传算法[13]是受到生物RNA分子编码和变异方式的启发，模拟生物分子进化的智能仿生算法．其特有的单链分子结构，大大降低了计算的成本，通过交叉、变异、颈环等分子间的变换，个体间的交流增大，扰动性加强，有利于全局寻优能力的增强[14]．受到这一启发，本文针对蝙蝠算法收敛精度低、易于陷入局部最优的缺点，提出利用RNA算法增加蝙蝠个体之间的联系，动态改变种群规模，加大扰动力度，使搜索更为全面，达到快速的收敛能力．

1 基于RNA遗传操作的改进蝙蝠算法

在觅食过程中，蝙蝠依靠精准的回声定位能力，能够快速地找到并捕获猎物，基于这种原理模拟出具有生物学机理的蝙蝠算法[15]．

1.1 蝙蝠算法的概述

文献[8]中，Yang教授归纳的数学模型为

 (1)

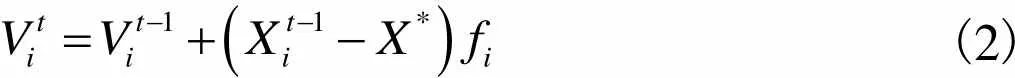
 (2)

 (3)

局部搜索过程中，位置的更新公式为

 (4)

 (5)

 (6)

1.2 RNA遗传操作与蝙蝠算法的结合

随着现代生物技术的发展，提出了使用生物分子作为计算载体的求解实际问题的方法，经过研究发现具备相同遗传特性的单链RNA结构更有利于信息的计算[16]．本文通过RNA算法与蝙蝠算法相结合的方式，利用RNA算法极强的变异性和扰动性，拓展蝙蝠算法的搜索空间，加快了算法前期的收敛速度，提高了收敛精度．

RNA分子是由4种碱基构成的：腺嘌呤(A)、尿嘧啶(U)、鸟嘌呤(G)和胞嘧啶(C)．4种碱基配对互补的原则为：腺嘌呤和尿嘧啶配对，鸟嘌呤和胞嘧啶配对．本文用到的RNA计算方法[17]如下．

图1 交叉操作

图2 变异操作

图3 颈环操作

对需要变异的蝙蝠个体的位置信息进行编码，将编码后的位置信息按照RNA算法的交叉、变异、颈环操作进行变换，得到新的位置信息编码，再反变换回位置信息传递给子代．

2 基于RNA遗传操作的改进蝙蝠算法

步骤2 启动蝙蝠进行随机搜索，每个蝙蝠进行一次寻优计算，记录下各个蝙蝠的寻优结果，找出当前最优解．

步骤3 将每只蝙蝠的寻优结果按照从小到大排序，取前1/4的蝙蝠个体进行保留．

步骤4 开始迭代计算．将上一步保留的蝙蝠个体进行自身变异，检测变异后的蝙蝠是否超界，超界蝙蝠用临界值替代，将变异后的蝙蝠与上一代保留的蝙蝠合并恢复至原种群数量的1/2．

步骤5 将现有种群进行RNA交叉、变异、颈环操作，检测变异后蝙蝠是否越界，超界蝙蝠用临界值替代，将变异后的蝙蝠与上一步的蝙蝠合并恢复至原种群数量，形成新一代蝙蝠种群．

步骤6 启动新种群进行最优化搜索，每个蝙蝠进行一次寻优计算，记录下各个蝙蝠的寻优结果，更新当前最优解．

步骤7 判断是/否完成迭代次数，“是”则执行步骤8，“否”则跳转至步骤3继续执行，迭代次数加1．

步骤8 结束算法，输出最优结果．

3 算法测试

为了证明基于RNA改进的蝙蝠算法性能，选取6个标准测试函数进行Matlab仿真．测试函数如表1所示．

表1 测试函数

Tab.1 Test function

表1中6种测试函数验证RNA优化蝙蝠算法的性能，通过搜索精度、算法可靠性和稳定性来直观的分析算法优化的性能．

算法的搜索精度通过合理的迭代次数后，算法寻找到的最优解、最差解和平均解来表征．算法的可靠性可以通过算法的成功率很好的表征，算法的成功率则是指在设定好的阈值下，算法达到标准的次数与总运行次数的比值．算法的收敛速度则是通过算法的平均收敛代数来表征的．算法的稳定性是通过标准差和相对误差来表征的．相对误差最佳性能比是指算法找到的最优解和理论最优解的差的绝对值与理论最优解的比值．

3.1 使用Sphere函数测试

表2 Sphere测试函数的运行结果统计

表3 各算法的稳定性和可靠性统计

由表2和表3以及图4可以分析出RNA蝙蝠算法与文献[17]算法在各方面均优于普通蝙蝠算法，虽然文献[17]算法的搜索精度略高于RNA蝙蝠算法，但RNA算法的稳定性高于文献[17]算法．

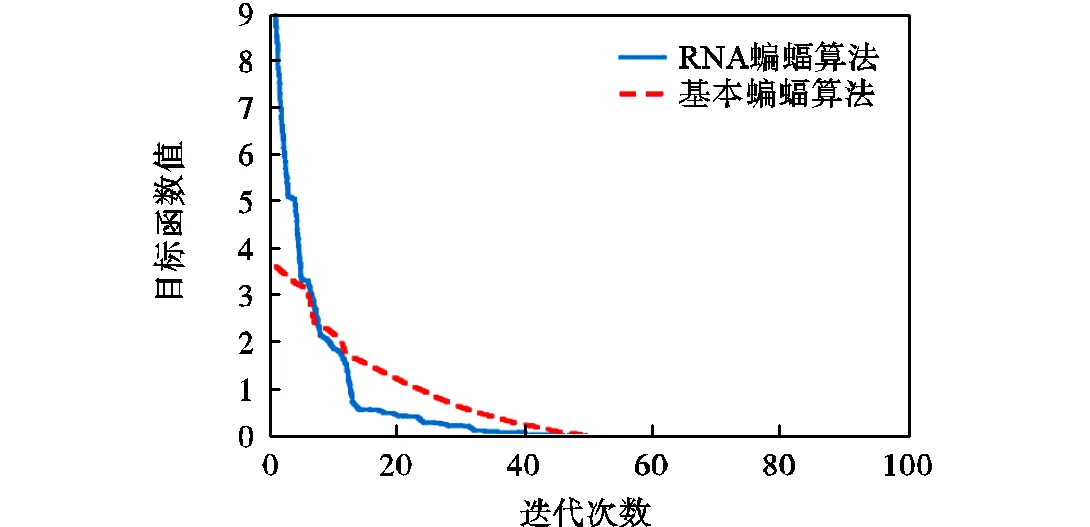
图4 各算法对Sphere测试函数的收敛曲线比较

3.2 使用Schaffer函数测试

表4 Schaffer测试函数的运行结果统计

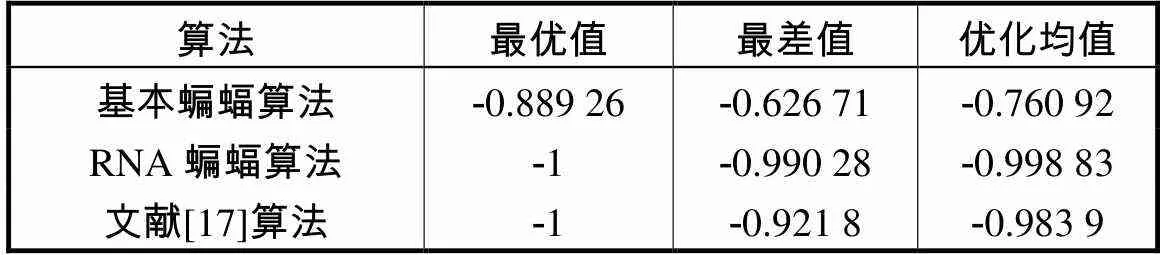
Tab.4 Statistical results of the Schaffer test function

表5 各算法的稳定性和可靠性统计

Tab.5 Stability and reliability statistics of the Schaffer test function

由表4、表5和图5可以分析出，RNA蝙蝠算法与文献[17]算法二者在寻优精度以及算法可靠性上基本相同．但RNA蝙蝠算法的稳定性(标准方差)优于文献[17]算法，除此以外RNA蝙蝠算法的成功率也高于文献[17]算法和基本蝙蝠算法．

图5 各算法对Schaffer测试函数的收敛曲线比较

3.3 使用Rastrgrin函数测试

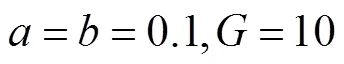
表6 Rastrgrin测试函数的运行结果统计

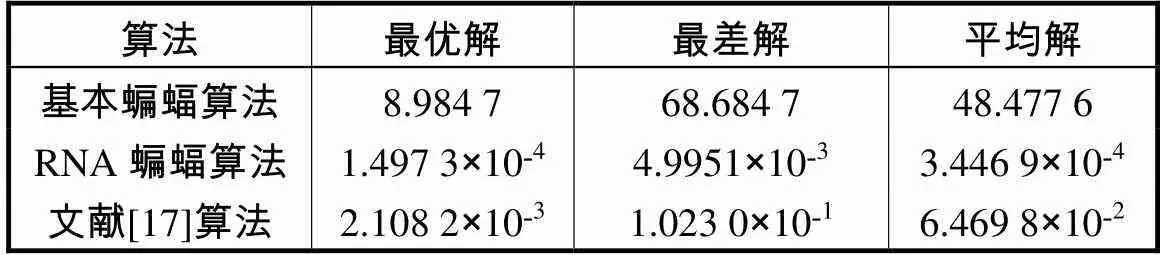
Tab.6 Statistical results of the Rastrgrin test function

表7 各算法的稳定性和可靠性统计

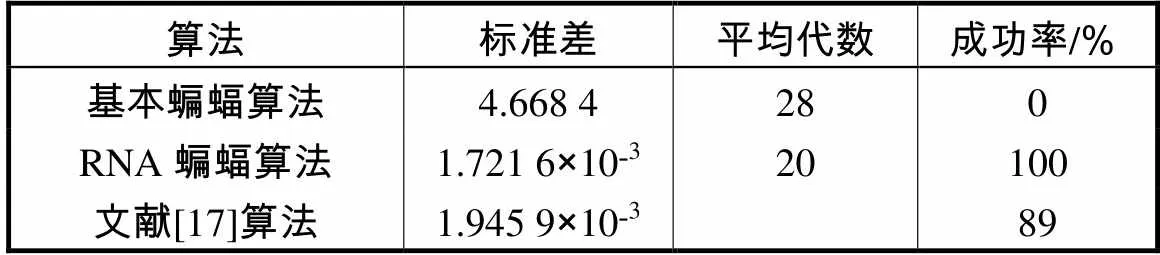
Tab.7 Stability and reliability statistics of the Rastrgrin test function

由表6、表7和图6可以分析出，RNA蝙蝠算法与文献[17]算法二者在稳定性方面相同，但RNA蝙蝠算法在搜索精度以及成功率上要好于文献[17]中的算法．除此以外RNA蝙蝠算法的收敛速度以及收敛精度都要高于普通蝙蝠算法．

图6 各算法对Rastrgrin测试函数的收敛曲线比较

3.4 使用Ackley函数测试

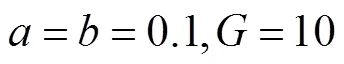
表8 Ackley测试函数的运行结果统计

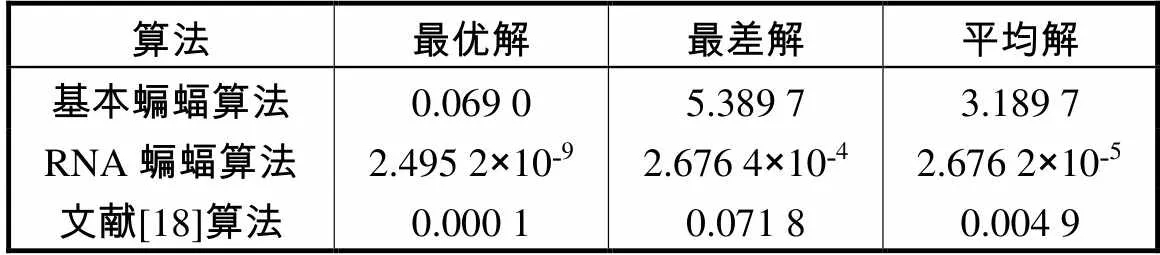
Tab.8 Statistical results of the Ackley test function

表9 各算法的稳定性和可靠性统计

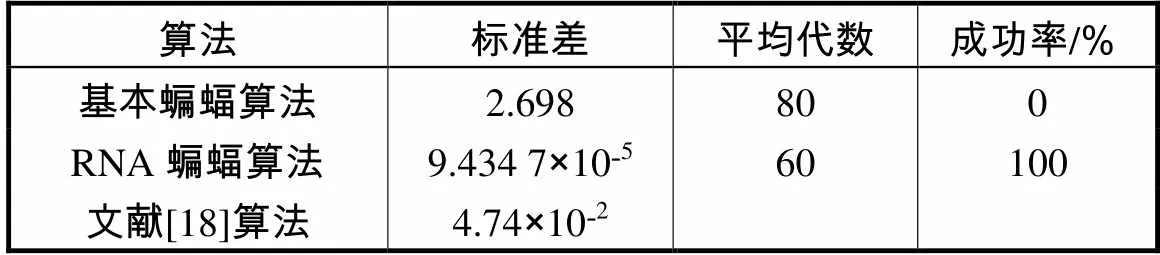
Tab.9 Stability and reliability statistics of the Ackley test function

由表8、表9和图7可以分析出，RNA蝙蝠算法在各项数据上均高于基本蝙蝠算法与文献[18]算法．在收敛精度方面，RNA蝙蝠算法远超基本蝙蝠算法和文献[18]算法，稳定性也强于基本蝙蝠算法与文献[18]算法．

图7 各算法对测试函数Ackley的收敛曲线比较

3.5 使用Griewank函数测试

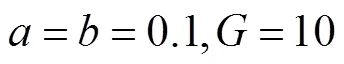
表10 Griewank测试函数的运行结果统计

Tab.10 Statistical results of the Griewank test function

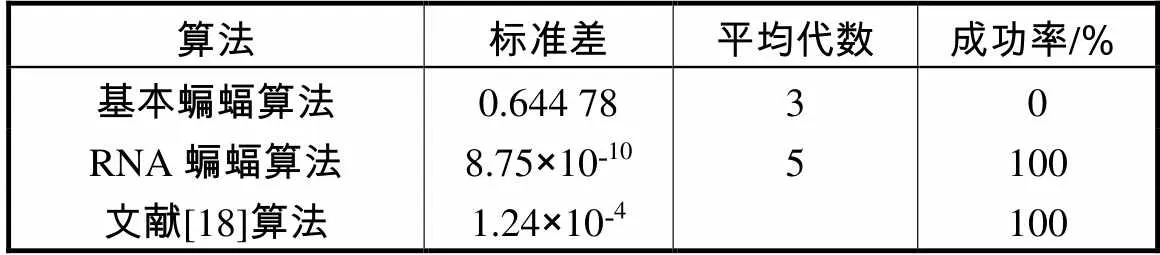
表11 各算法的稳定性和可靠性统计

由表10、表11和图8可以分析出，RNA蝙蝠算法与文献[18]算法二者在成功率上相同且均高于基本蝙蝠算法，但在算法稳定性方面还是RNA蝙蝠算法更强一些，此外虽然基本蝙蝠算法的收敛速度略高于RNA蝙蝠算法，但收敛精度远低于RNA蝙蝠 算法．

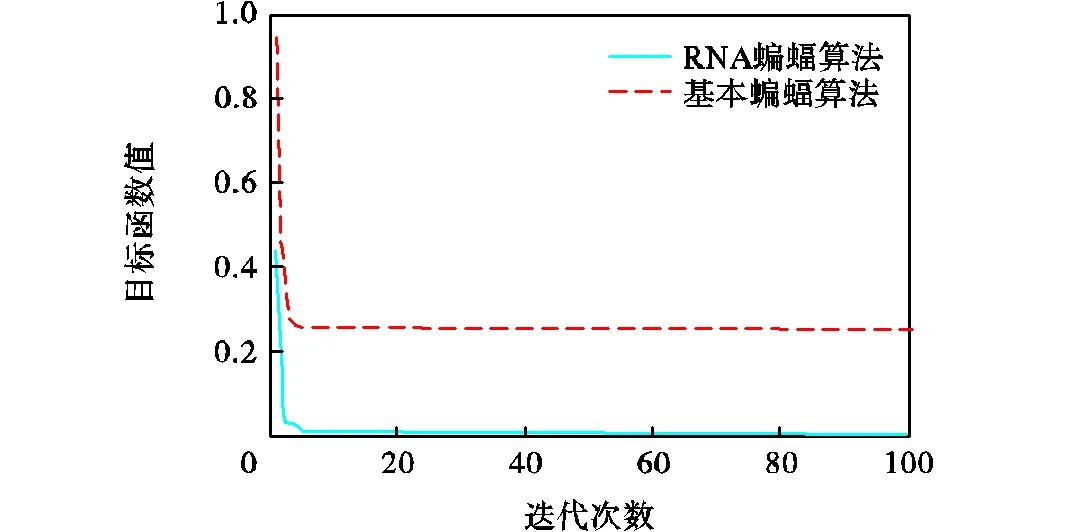
图8 各算法对Griewank测试函数的收敛曲线比较

3.6 使用Rosebrock函数测试

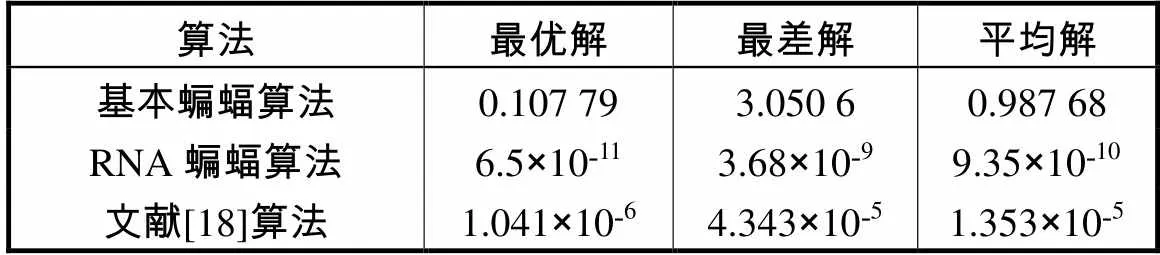
表12 Rosebrock测试函数的运行结果统计

Tab.12 Statistical results of the Rosenbrock test function

表13 各算法的稳定性和可靠性统计

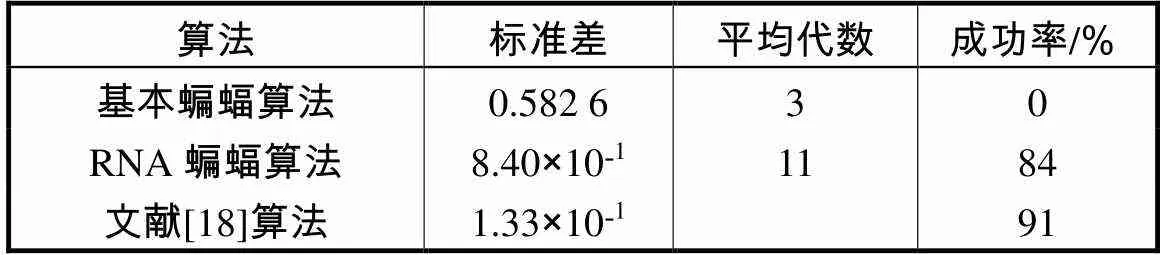
Tab.13 Stability and reliability statistics of the Rosen-brock test function

由表12、13和图9可以分析出文献[18]算法在算法的可靠性上略好于RNA蝙蝠算法，但RNA算法的搜索精度要高于文献[18]算法．在算法稳定性方面二者相似，文献[18]算法稳定性略高．

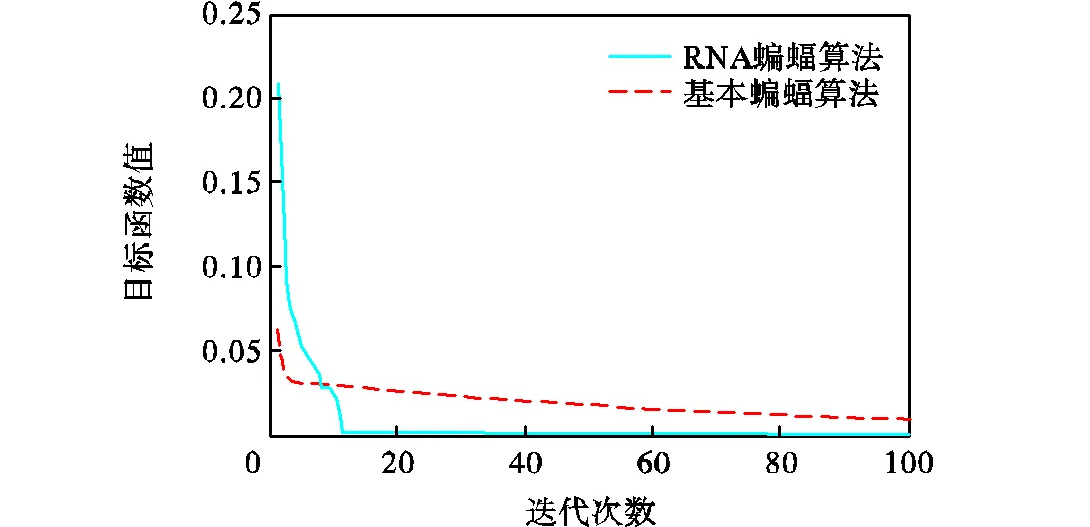
图9 各算法对Rosebrock测试函数的收敛曲线比较

4 结 语

蝙蝠算法是一种新型智能仿生算法．该算法由Yang教授提出，是一种搜索全局最优解的有效算法，该算法在准确性和有效性等方面优于其他算法．但算法也存在着一些局限性，在受到局部极限约束后将无法摆脱，因而很难跳出局部最优解，本文提出的RNA蝙蝠算法针对这一问题对蝙蝠算法进行改进，运用RNA遗传算法的各种变异策略增加蝙蝠算法的扰动性，加大蝙蝠之间的交流，经过实验证明，算法可以快速找到最优解，避免在局部最优解附近进行大量计算浪费工作效率．

［1］ Hamidzadeh J. Weighted support vector data description based on chaotic bat algorithm[J]. Impact Factor，2017，60(3)：550-553.

［2］ Chaib L，Choucha A. Optimal design and tuning of novel fractional order PID power system stabilizer using a new metaheuristic bat algorithm[J]. Ain Shams Engineering Journal，2015，8(2)：113-120.

［3］ Chakri A，Khelif R. New directional bat algorithm for continuous optimization problems[J]. Expert Systems with Applications，2017，69：159-175.

［4］ Ahmadianfar I，IAdibA. Optimizing multireservoir operation：Hybrid of bat algorithm and differential evolution[J]. Journal of Water Resoures Planning and Management，2016，142(2)：25-27.

［5］ Chen Meiwen，Zhong Yiwen，Wang Lijin，et al. Bat algorithm with one-dimension learning[J]. Journal of Chinese Computer Systems，2015，36(11)：2614-2616.

［6］ 吴华锋，陈信强，毛奇凰，等. 基于自然选择策略的蚁群算法求解TSP问题[J]. 通信学报，2013，34(4)：166-170.

Wu Huafeng，Chen Xinqiang，Mao Qihuang，et al. Natural selection of ant colony algorithm for solving TSP problems[J]. Journal of Communication Strategy，2013，34(4)：166-170(in Chinese).

［7］ 秦全德，程 适，李 丽，等. 人工蜂群算法研究综述[J]. 智能系统学报，2014，9(2)：127-135.

Qin Quande，Cheng Shi，Li Li，et al. An overview of artificial bee colony algorithms[J]. Journal of Intelligent Systems，2014，9(2)：127-135(in Chinese).

［8］ Yang X S. A new meta heuristic bat-inspired algorithm[J]. Nature Inspired Cooperative Strategies for Optimization，2010：65-74.

［9］ 盛孟龙，贺兴时，丁文静. 蝙蝠算法的全局收敛性分析[J]. 纺织高校基础科学学报，2013， 26(4)：543-547.

Sheng Menglong，He Xingshi，Ding Wenjing. Analysis of bat algorithm’s global convergence[J]. Basic Sciences Journal of Textile Universities，2013，26(4)：543-547(in Chinese).

［10］ 李雅梅，曹益华. 基于Powell机制的改进蝙蝠算法[J]. 微电子学与计算机，2015，32(3)：73-80.

Li Yamei，Cao Yihua. An improved bat algorithm based on powell mechanism[J]. Microelectronics & Com-puter，2015，32(3)：73-76(in Chinese).

［11］ 屈迟文，傅彦铭，侯勇顺. 融合入侵杂草算子的蝙蝠算法[J]. 计算机应用与软件，2015，32(4)：243-246.

Qu Chiwen，Fu Yanming，Hou Yongshun. Bat algorithm fused with invasive weed operator[J]. Computer Applications and Software，2015，32(4)：243-246(in Chinese).

［12］ 尚俊娜，刘春菊，岳克强，等. 具有自学习能力的变异蝙蝠优化算法及性能仿真[J]. 系统仿真学报，2017，29(2)：301-308.

Shang Junna，Liu Chunju，Yue Keqiang，et al. Variation bat algorithm with self-learning capability and its property analysis[J]. Journal of System Simulation，2017，29(2)：301-308(in Chinese).

［13］ Tao Jili，Wang Ning. DNA computing based RNA genetic algorithm with applications in parameter estimation of chemical engineering processes[J]. Computers and Chemical Engineering，2017，31(12)：1602-1618.

［14］ Wang Kangtai，Wang Ning. A novel RNA genetic algorithm for parameter estimation of dynamic systems[J]. Chemical Engineering Research and Design，2010，88(11)：1485-1493.

［15］ 肖辉辉，段艳明. 基于DE算法改进的蝙蝠算法的研究及应用[J]. 计算机仿真学报，2014， 3(1)：272-301.

Xiao Huihui，Duan Yanming. Research and application of improved bat algorithm based on DE algorithm[J]. Journal of Computer Simulation，2014，31(1)：272-301(in Chinese).

［16］ 罗 亮，吴文峻，张 飞. 面向云计算数据中心的能耗建模方法[J]. 软件学报，2014，25(7)：1371-1387.

Luo Liang，Wu Wenjun，Zhang Fei. Modeling method of energy consumption for cloud computing data center[J]. Software Journal，2014，25(7)：1371-1387(in Chinese).

［17］ 肖辉辉. 基于单纯形法的蝙蝠算法[J]. 河池学院学报，2016，36(2)：60-66.

Xiao Huihui. Bats algorithm based on simplex method [J]. Journal of Hechi University，2016，36(2)：60-66(in Chinese).

［18］ 岳伟娜，马吉明，苏日建，等. 基于反向学习机制的蝙蝠算法[J]. 湖北民族学院学报：自然科学版，2016，34(3)：251-255.

Yue Weina，Ma Jiming ，Su Rijian，et al. Reverse learning mechanism based on bat algorithm[J]. Journal of Hubei Institute for Nationalities：Natural Science Edition，2016，34(3)：251-255(in Chinese).

(责任编辑：王晓燕)

Improved Bat Algorithm Based on RNA Genetic Algorithm

Geng Yanxiang1, 2，Zhang Liyi1, 2，Sun Yunshan2，Fei Teng2，Jiang Shixian2，Ma Jiajun2

1. School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China；2. School of Information Engineering，Tianjin University of Commerce，Tianjin 300134，China)

As a new metaheuristic algorithm，the bat algorithm has excellent search capability and can be applied to a variety of scenarios. However，the bat algorithm has problems with regard to its convergence rate and precision and the lack of interaction between individuals. In response to these deficiencies，the RNA genetic algorithm was introduced to enhance the interaction between individuals. Through the change of information，such as crossover and mutation，the search speed and precision of the algorithm can be improved. The test functions proved that the improved algorithm has good robustness，reliability and stability，which considerably improve the search capability of the bat algorithm.

bat algorithm；RNA inheritance；crossover；variation

10.11784/tdxbz201801027

TP399

A

0493-2137(2019)03-0315-06

2018-01-03；

2018-05-31.

耿艳香（1983—  ），女，博士研究生，实验师，gengyanxiang@163.com.

张立毅，zhangliyi@tucu.edu.cn.

国家自然科学基金资助项目(61401307)；国家软科学研究计划资助项目(2014GXS4D089)；天津市应用基础与前沿技术研究计划资助重点项目(14JCZDJC32600)；天津市高等学校科技发展基金计划资助项目(20110709)；天津市应用基础与前沿技术研究计划资助项目(15JCYBJC17100)；中国物流学会资助项目(2014CSLKT3-16)；天津企业科技特派员计划项目(18JCTPJC66900).

the National Natural Science Foundation of China(No.61401307)，the National Soft Science Research Plan of China (No.2014GXS4D089)，the Tianjin Key Research Program of Application Foundation and Advanced Technology (No.14JCZDJC32600)，the University Technology Development Fund of Tianjin(No.20110709)，the Tianjin Key Research Program of Application Foundation and Advanced Technology(No.15JCYBJC17100)，the Key Program of the Chinese Society of Logistics(No.2014CSLKT3-16)，the Tianjin Enterprise Science and Technology Correspondent Project (No.18JCTPJC 66900).