北大秦簡《魯久次問數于陳起》衡間圖淺探*
曹方向
關鍵詞: 北大秦簡;衡間圖;四卦
北京大學藏秦簡《魯久次問數于陳起》的“三方三圓”,是建立在蓋天説基礎上的一種宇宙模型。這種模型在較早的古書中主要見於《周髀算經》。兩年前我們因解釋簡文的“六間”,粗略談到簡文“三方三圓”即《周髀算經》夏至、春秋兩分和冬至點所在的内、中、外衡。至於三衡在簡文中特殊的命名方法,當時深感困惑。[注]曹方向: 《初讀北大秦簡〈魯久次問數于陳起〉》,簡帛網2015年11月18日,http: //www.bsm.org.cn/show_article.phpid=2360。推敲之後,我們懷疑《周髀算經》的衡間圖可能已經提供了爲三衡命名的思路。由此不僅可以理解簡文“三衡”的特殊名稱,對簡文後段的“四卦”,也可以做出比較合理的解釋。因此寫成小文,希望得到更多先生批評指教。
一、 “三方三圓”和七衡圖
我們先根據整理者提供的釋文和專家筆談收録的見解,[注]韓巍: 《北大秦簡〈魯久次問數于陳起〉初讀》,《北京大學學報(哲學社會科學版)》2015年第2期,第29—36頁;韓巍、鄒大海: 《北大秦簡〈魯久次問數于陳起〉今譯、圖版和專家筆談》,《自然科學史研究》2015年第2期,第232—266頁。韓巍先生的意見見於這兩文,合稱爲整理者意見。將相關簡文抄録如下:
曰: 地方三重,天148圓三重,故曰: 三方三圓,規矩、水繩、五音、六律、六簡(間)皆存。[注]簡文“水繩”,整理者未破讀。徐學炳、王寧先生等以爲當改讀爲“準繩”。向按:“水”作準器,“繩”作懸器,“水”、“繩”爲實物,“準”、“衡”爲功能。同理,“規”、“矩”分别用來畫方、圓,“規”、“矩”是實物工具,畫方、圓則是功能。竹書以“規、矩、水、繩”並列,是從實物層面説。整理者不破讀是正確的。徐學炳: 《北大秦簡〈魯久次問數于陳起〉補釋》,簡帛網2015年4月21日,http: //www.bsm.org.cn/show_article.phpid=2216;王寧: 《讀〈殷高宗問於三壽〉散札》,復旦大學出土文獻與古文字研究中心2015年5月17日,http: //www.gwz.fudan.edu.cn/Web/Show/2525。始諸黄帝139、諯(顓)玉(頊)、堯、舜之智,循鯀、禹、皋陶、羿、箠之巧,以作命下之灋,以立138鐘之副: 副黄鐘以爲十二律,以印久下爲十二時,命曰十二字,生五音、十日、廿八日137宿。道頭到足,百體各有司殹(也),是故百體之癰,其瘳與死各有數。[注]向按: 《春秋繁露》人副天數:“人有三百六十節,偶天之數也。”《潛夫論》相列:“一人之身,而五行八卦之氣具焉。”曰: 大方大136圓,命曰單薄之參(三);中方中圓,命曰日之七;小方小圓,命曰播之五。故曰: 黄149鐘之副、單薄之參(三)、日之七、播之五,命爲四卦,以卜天下。150
這段簡文談地方、天圓,和《周髀算經》所持的“蓋天説”一致。《周髀算經》以天圓地方爲大前提來描述太陽周年運動時,曾將其運動軌道設想爲以北極爲圓心的七條同心圓軌道,稱爲“七衡”。其中最小、最大的同心圓所代表的“衡”,分别稱爲内、外衡;從内往外數第四個同心圓,則稱爲中衡:“内第一,夏至日道也。中第四,春秋分日道也。外第七,冬至日道也。”[注]錢寶琮校點: 《算經十書》,中華書局1963年,第46頁。七衡之中有六個區間,是爲“六間”。簡文另有“大方大圓”、“中方中圓”、“小方小圓”,和《周髀算經》的内、中、外衡有整齊的對應關係。
爲方便後文討論,我們將《周髀算經》的“七衡圖”轉録於下。[注]圖片取自陳遵媯: 《中國天文學史》(第一册),上海人民出版社1980年,第131頁。

圖一
簡文“三方三圓”分别有特殊的名稱,而《周髀算經》僅稱外、中、内三“衡”。整理者因此名稱爲典籍所無,暫未詳考。近見陳鐿文、曲安京先生從數學角度論證,認爲三衡是根據内、中、外衡的半徑來命名。[注]陳鐿文、曲安京: 《北大秦簡魯久次問數于陳起中的宇宙模型》,《文物》2017年3月,第93—96頁。以下我們根據《周髀算經》提供另一種解釋。
按《周髀算經》“七衡”圖,外、中、内三衡是兩分、兩至日所在。對照衡間圖,一目了然。對本篇簡文來説尤爲重要的是,經文描述了這三衡的日照情况。辦法是將三衡各十二等分,利用十二地支和卦位加以標記,日出、日入點各對應一個地支,以此區分太陽照射和不能照射的範圍(引文詳後)。
我們看到,簡文“印久下爲十二時”,而後“命爲十二字”,相當於在“衡”上作標記。這和《周髀算經》的計算思路是一致的。整理者在“久”字後括注“記”,通釋句意爲“給天下打上印記,分爲十二月”,也有道理。“十二字”即十二支。稍微可以補充的是,“十二時”並不一定是“十二月”。《周禮·春官》馮相氏“掌十有二歲,十有二月,十有二辰,十日,二十有八星之位。”同書“哲蔟氏”鄭玄注:“日,謂從甲至癸;辰,謂從子至亥;月,謂從娵(或作“陬”)至荼;歲,謂從攝提格至赤奮若;星,謂從角至軫。”[注]孫詒讓: 《周禮正義》(八),中華書局2008年,第2103頁。以“十二”爲數者,有歲、月、辰,都算是“十二時”。根據馬王堆帛書《禹藏圖》,李零先生曾指出,古時年、月、日都有兩個系統,一種是四分的“大時”,一種是十二分的“小時”。[注]李零: 《中國方術正考》,中華書局2010年,第111—114頁。所謂《禹藏圖》,見周一謀、蕭佐桃主編: 《馬王堆醫書考注》,天津科學技術出版社1988年,第347頁;裘錫圭主編: 《長沙馬王堆漢墓簡帛集成(陸)》,中華書局2014年,第100頁。這樣看來,簡文“十二時”的“時”,可能包括年、月、日的十二分法,不僅僅是“十二月”。
在“十二時”前文,有十二律,後文有“五音、十干、二十八宿”。整理者認爲,“十干”可能就是標記一旬十日。[注]向按: 《左傳》昭公五年:“日之數十。”《淮南子·天文》申論云:“凡日,甲剛、乙柔、丙剛、丁柔,以至於癸。”但古籍説“十日”,其實也指一年分十個月。《爾雅·釋天》有“月陽”(《史記索隱》所謂“月雄”)和“月名”(《史記索隱》所謂“月雌”):“月在甲曰畢,在乙曰橘,在丙曰修,在丁曰圉,在戊曰厲,在己曰則,在庚曰窒,在辛曰塞,在壬曰終,在癸曰極: 月陽。”又有十二月“月名”:“正月爲陬,二月爲如,三月爲寎,四月爲餘,五月爲皋,六月爲且,七月爲相,八月爲壯,九月爲玄,十月爲陽,十一月爲辜,十二月爲塗。”“月名”已見於長沙子彈庫戰國帛書,是陰曆月。與此相應,“月陽”是陽曆月,也就是一年分十個月,依次用十天干來表示。簡文此處没有足够的證據可以判斷到底是十天還是十個月,但“十日”都是用十天干來標記,應無疑義。考放馬灘秦簡《日書》乙種,既有十二律和一日之中太陽運行位置的對應表,[注]參看陳偉主編: 《秦簡牘合集(釋文注釋修訂本)(肆)》,武漢大學出版社2016年,第112—113頁。也有五音、十二地支、十干和日辰的對應表。[注]陳偉主編: 《秦簡牘合集(釋文注釋修訂本)(肆)》第98頁。例如簡182第七欄,與夾鐘相應的太陽位置在參阿。程少軒先生根據式圖分析指出,與之對應的方位是正東方、日辰是《淮南子·天文》所述“旦明”。[注]陳偉主編: 《秦簡牘合集(釋文注釋修訂本)(肆)》第113頁。所言甚是。查簡197第一欄:“徵位甲乙、卯未亥,主東方,【時】平旦。”以此爲參照,可以建立十二律、十二時(十二月或十二辰)、十干(十天干、十日或十月)、十二支、五音的對應關係。
我們認爲,簡文也是將每一個“圓”十二等分,描述其日照情况,從而爲三衡分别命名。
簡文“大方大圓”命名爲“單薄之參”,整理者將“參”讀爲“三”。可從。“大方大圓”即七衡圖的“外衡”,是冬至點所在。冬至是一年中白晝最短的一天,也是以四分曆爲代表的先秦曆法的起算點。簡文在“黄鐘之副”後面先列出“大方大圓”即外衡,可能是爲了突出冬至的起點意義。冬至(以及整個冬天)陽光較爲微弱。“單”即微弱,“薄”即晦暗。根據《周髀算經》,冬至日太陽的視運動:“冬至晝極短,日出辰而入申。陽照三,不履九,東西相當正南方。”又:“(冬至)日出艮而入神(坤),見日光少,故曰寒。”其中“見日光少”,和簡文“單薄”二字語義相應。這就是説,在七衡圖的“外衡”上,用十二地支等分十二份(參看下圖二),冬至日太陽在辰位升起,經過三個地支(巳、午、未),在申位落下。冬至日即使白天,微弱的陽光照射三個地支位。因而將冬至所在的外衡命名爲“單薄之三”。

圖二
中方中圓的“日之七”,“日”可以直接理解爲日光照射。春秋兩分日,晝夜平分。也就是説,將中衡十二等分,用十二支標記,日出於卯位、入於酉位(參看圖二)。卯、辰、巳、午、未、申、酉,共計七個地支位爲太陽照射。
小方小圓對應的是内衡,即夏至所在。《周髀算經》描述此時的日照情形爲:“夏至晝極長,日出寅而入戌,陽照九,不覆三,東西相當正北方。”所謂“不覆三”,是説夏至日太陽出於寅位、入於戌位,子、丑、亥三個地支位照射不到(參看圖二)。按“播之五”的“播”,在古籍中訓爲“棄”。《廣韻》:“播,放也,棄也。”《尚書·多方》“播天命”,孔傳訓“播”爲“播棄”。《玉篇》:“播,棄也。”正用《多方》及孔傳。和《周髀算經》“不覆”語意相應。綜合外衡、中衡看,“播”在簡文中指的是“不被太陽光照射”。就修辭手法而言,中衡“日之七”和内衡“播之五”屬於互文。
冬至時分外衡的計算法,不計日出、日入對應的兩個地支。所以“單薄之三”,指巳、午、未三位。如此,兩分日應該説“日之五”,夏至日應該説“播之三”,似乎和簡文不吻合。其實就數目而言,《周髀算經》説“陽照九、不覆三”,可以説是“三、九”兩分法,簡文兩分日和夏至用的却是“五、七”兩分法。究其實質,兩者的差别僅僅在於是否計算日出、日入對應的地支。把日出、日入相應的地支當成起止點,如果計入起止點,夏至日“陽照”爲“九”,兩分日“陽照”爲“七”。同樣,計入起止點,夏至日“不覆”爲“五”,兩分日“不覆”是“七”。也就有兩分日“日之七”和夏至日“播之五”的説法。借用《周髀算經》,就是“陽照七,不覆五。”
外衡和中衡、内衡的計算標準何以不同?我們推想有兩個理由。第一,就字面意義而言,爲外衡命名所用的“單薄”一詞,如前所述,描寫的是日照强弱,而爲中衡、内衡命名所用的“日”和“播”,描述的是日照範圍(這個“範圍”是各衡上對應的地支位)。“單薄”强調是冬至日白天的光照很弱,不計日出、日入點。爲中衡、内衡命名時,計算的是日照範圍,自可計入日出、日入點。第二,可能還考慮到十二律有五、七兩分法。例如放馬灘秦簡《日書》乙種簡193第三欄:“黄鐘以至姑洗皆下生,三而二。從中吕以至應鐘皆上生,三而四。”就是把十二律作五、七分。相同的五、七分法,也見於《吕氏春秋·音律》等傳世文獻(引文詳下節)。簡文明確説過要引入十二律,以配合四卦,將太陽所照的地支也采用五、七兩分法,似乎也是值得考慮的。
綜上,“三方三圓”的命名,其依據實際是七衡圖外、中、内三衡的日照情况。現在再回看前文的“六簡”,似乎也和七衡有關。“六簡”整理者破讀爲“六間”,認爲是指“六陰律”。其實可能就是指衡間圖的“六間”。[注]就典籍用例而言,“六律”可以代表“十二律”,特别是和“五音”並列的場合,“十二律”更是常常以“六律”的形式和“五音”構成並列結構。如《淮南子·泰族訓》:“别清濁五音六律相生之數。”不僅如此,“十二律”分開説,在秦簡中又稱爲“間吕六律”(如放馬灘秦簡《日書》乙種第284、285簡),即六間律、六吕律。因此我們懷疑分開説陰陽律時,《周禮》的“六律六間”,不排除是後來所改(《春官》三處提到六律六同,則是統一修改的結果)。如前所述,《周髀算經》“七衡”之中的六個區間就是“六間”。簡文“大方大圓”、“中方中圓”、“小方小圓”既然正好對應《周髀算經》的内、中、外衡,則“六間皆存”的“六間”,似有可能指“七衡六間”的“六間”。簡文“皆存”,當是説規矩、水繩、五音、六律、六間都存在於“三方三圓”内。
三、 “三方三圓”和四卦
簡文説十二律、三方三圓“命爲四卦”,把數學和易學甚至數術混而爲一,也就是要構建一個卦位和十二律、衡間圖兼容的模型。這在古人看來似是理所當然。劉徽在《九章算術》就寫道:“(伏羲)作九九之術以合六爻之變。”[注]郭書春: 《九章算術譯注》,上海古籍出版社2009年,正文第1頁。但整理者將此處語譯爲“所以‘黄鐘之二’、‘單薄之三’、‘日之七’、‘播之五’合稱‘四卦’”,似不盡然。
我們認爲簡文爲“三方三圓”命名之後,文意已告一段落。“命爲四卦”是説把“黄鐘之副”、“三方三圓”依據四卦進行排列。大家知道,卦位除了對應四方、四時外,在“月令”類文獻中暗示五音十二律、干支、五行的排列組合;在《周髀算經》的天文學説中,又暗示太陽在三衡的照射範圍(引文詳後)。這些天地間重要的“數”,也就是五音、干支、十二律、二十八宿等,按照八卦方位組合排列成圓形圖式,可以施用于天文、曆法、占卜等方面。因此説“黄鐘之副”、“三方三圓”“命爲四卦”以後可以“卜天下”。
“黄鐘”之數和八卦有關。劉徽《九章算術》:“(黄帝)建曆紀、協律吕,用稽道原,然後兩儀四象精微之氣可得而效焉。”《周禮》“大師”鄭玄注:“黄鍾,初九也,下生林鍾之初六,林鍾又上生大蔟之九二,大蔟又下生南吕之六二……”又是直接用乾六爻和坤六爻對應十二律。[注]參看李道平: 《周易集解纂疏》“鄭氏爻辰圖”,中華書局1994年,第16頁。
十二律和“四卦”的關聯,《吕氏春秋》十二紀還有更清楚的對應。《吕氏春秋》有以黄鐘爲起算點生成十二律的資料:“黄鐘生林鐘,林鐘生太蔟,太蔟生南吕,南吕生姑洗,姑洗生應鐘,應鐘生蕤賓,蕤賓生大吕,大吕生夷則,夷則生夾鐘,夾鐘生無射,無射生仲吕。三分所生,益之一分以上生。三分所生,去其一分以下生。黄鐘、大吕、太蔟、夾鐘、姑洗、仲吕、蕤賓爲上,林鐘、夷則、南吕、無射、應鐘爲下。”十二月各有對應的律吕,而且各季度還對應一個數值,即: 孟春(太蔟)、仲春(夾鐘)、季春(姑洗)“其數八”;孟夏(仲吕)、仲夏(蕤賓)、季夏(林鐘)“其數七”;孟秋(夷則)、仲秋(南吕)、季秋(無射)“其數九”;孟冬(應鐘)、仲冬(黄鐘)、季冬(大吕)“其數六”。
據《五行大義》,十二個月的“八、七、九、六”依次是木、火、金、水的成數(中央土,其數五,此從略)。[注]此據王利器《吕氏春秋注疏》第一册,巴蜀書社2002年,第12頁。文獻不止一見。如《墨子·迎敵祠》、《尚書大傳》述四方來敵,迎敵時要注意各個方位對應的成數(具體包括堂高、人數及年齡、神數及其長度、弓弩數等)、服色等。例如,“敵以東方來”,用成數八(孫詒讓已注明)、服色青;從南方來,迎敵用成數七,服色赤;從西方來,用成數九,服色白;從北方來,用成數六,服色黑。[注]吴毓江: 《墨子校注》,中華書局2006年,第875—876頁、877—878頁。在五行學説中,這對應於正東、南、西、北四方和四時(四季)。如虞翻解《周易·系辭上》“兩儀生四象”:“乾二五之坤,成坎、離、震、兑。震春、兑秋、坎冬、離夏。”[注]李道平: 《周易集解纂疏》第601頁。《周易》“大衍之數”,坎、離、震、兑四卦的數也是這四個數。成數“八、七、九、六”及五行方位有如下表:
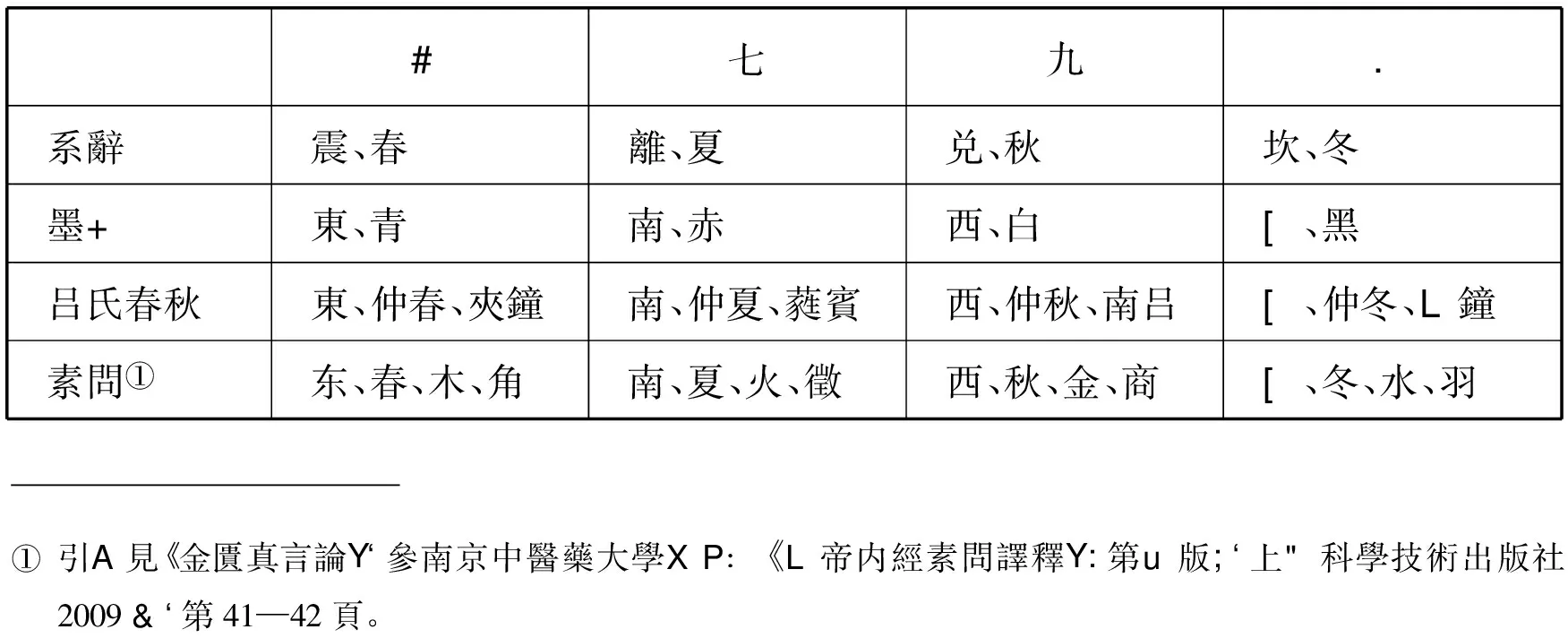
表一
簡文“黄鐘之副”是指從黄鐘生出的十二律,其中夾鐘、蕤賓、南吕、黄鐘四律分别和震、離、兑、坎“四卦”相應。震、離、兑、坎按上述方位排列成圖(即坎離正南北、震兑正東西),就是“後天八卦圖”的“四正卦”。[注]朱子: 《周易本義》,參朱傑人主編: 《朱子全書》第一册,上海古籍出版社2010年,第22頁;李道平: 《周易集解纂疏》第26頁。無獨有偶,《周髀算經》也有這個卦圖。
儘管没有提到黄鐘律數,但《周髀算經》曾説:“冬至從坎,陽在子,日出巽而入神(坤),見日光少,故曰寒。夏至從離,陰在午,日出艮而入乾,見日光多,故曰暑。”明確將“坎、離”和地支的“子、午”分别對應,排在正南北方。這是將兩至日(原文没有明寫兩分日的對應關係)擺在後天八卦圖上,來描述日出入。一衡十二等分,按照十二地支描述時,冬至日“日出辰而入申”,用卦位的等價描述即經文“日出巽而入坤”。[注]江曉原: 《〈周髀算經〉新論·譯注》,上海交通大學出版社2015年,第111—112頁。他皆准此。轉成圖形,如前文圖二所示。爲便於參看後文所引放馬灘簡,圖中標出後天八卦,也標出相應的干支。圖中三個粗綫圓表示三衡,下方陰影部分表示外衡日出入點(“出辰入申”及其等價表述“出巽入坤”)及走向。
放馬灘秦簡《日書》簡196~200第一欄、簡179~190第七欄分别有如下表左、中列的内容(釋文均有節略,而且個别簡文語序有調整),通過下表右列《淮南子》可以建立其對應關係:

表二
簡文“參阿”、“毚都”等,程少軒先生認爲《淮南子·天文》描述太陽晝夜運動位置時提到的“曲阿”、“昆吾”等與之存在對應關係,其説有理。[注]陳偉主編: 《秦簡牘合集(釋文注釋修訂本)(肆)》第113—114頁。這樣,以上内容以“五音”爲序,按四方、四時(四季顔色)與五行組合排列之外,十二支按五行三合局列入其中,又引入十二律、十二“時辰”,用以標記太陽一晝夜的運動。類似的資料在放馬灘秦簡中不止一見,此不具引。
由此,根據放馬灘秦簡《日書》的五音、五行、十干、十二支對應表,《吕氏春秋》十二律和分至的對應,加上《周髀算經》分至和後天卦位的對應,本簡提到的各種“數”彼此都可以建立聯繫。尤其有趣的是,上揭各種文獻都是文字表述(在竹簡上分欄書寫或許具有表格意味),要是轉换爲圖式(如上圖二),確定四方、四時,又和卦位重疊,這可能就是簡文“命爲四卦”的理由所在。
四、 結 語
本篇竹書談論數學知識在生活中的種種用處,采用問答形式,是戰國諸子百家活躍之際盛行的學術討論方式。其中談到亭臺樓閣、馳騁田獵,[注]向按: 簡146“弋獵置放御”,學者認爲“置”是衍文,應該可信。整理者認爲“御”是“禁止”之意。肖燦先生改讀爲“圉”,“放圉”是“放養”和“圈養”。似非定論。我們認爲“御”可能就是駕馭的意思。“御”指駕馭,例多不贅。古人所謂“放”,可以指放縱身心在外遊玩,而且可以和“獵”並列。例如《漢書·王褒傳》“放獵”顔師古注:“遊放及田獵。”因此,“放御”可以理解爲放縱身心駕駛車馬出遊。又,典籍常見“弋獵”和宴飲、遊賞之事並列。《老子》:“馳騁弋獵,令人心發狂。”《國語·越語下》:“王其且馳騁弋獵,無至禽荒。”《史記·范雎蔡澤列傳》:“且夫三代所以亡國者,君專授政,縱酒、馳騁、弋獵,不聽政事。”典籍“馳騁”,不僅指騎馬出遊,也指以其他方式外出遊玩。“放御”實際上相當於“馳騁”。所謂“弋獵放御”,就是“馳騁弋獵”,加上前文“高閣臺榭”,大體和《范雎蔡澤列傳》“縱酒、馳騁、弋獵”相當。符合先秦時代的貴族生活情景。再者,在傳世文獻中,很少强調秦代對數學作出的特殊貢獻。把算題匯集成書,也很難説是始於秦代。本篇竹書作者和《算書》甲種編者,是否如整理者所説“很可能是同一人”,恐怕還大有推敲的餘地。
古人的論著,常常以單篇形式在學者之間轉抄流傳,對此,余嘉錫先生《古書通例》有很好的論述。終究不能排除本篇竹書以單篇形式流傳的可能性。如果不考慮尚未公布的北大秦簡數學文獻,單獨就本篇而言,視爲諸子文獻,應無問題。[注]向按: 從簡文看,“陳起”其人至少在魯久次看來是位數學名家。甚至可以認爲,戰國百家爭鳴的時代,曾有一個擅長數學的學派,而陳起是代表人物之一。將一個學派或專業領域的代表人物尊稱爲“子”,正是東周以來的習慣。不能完全排除簡文“陳起”是《周髀算經》“陳子”的可能性。按《後漢書》載馬融《廣城賦》寫飛鳥之多,無法計算,以至“隸首策亂、陳子籌昬”。舊注以爲“陳子”指漢朝陳平。《管城碩記》認爲,“隸首”之“策”和“陳子”之“籌”,可能都是和數學有關的算籌,不一定指計謀,馬氏所説“陳子”當指《周髀算經》的“陳子”(參看徐文靖標點: 《管城碩記》,中華書局1998年,第483—484頁)。考《晋書·律曆志下》:“使研桑心算,隸首運籌。”計研、桑弘羊均擅長數學計算,可以和計研、桑弘羊、隸首並列的“陳子”,確實更有可能是《周髀算經》的“陳子”。這就是説,作爲數學名家的“陳子”,《周髀算經》所記並非孤例。目前尚不能直接把陳起和《周髀算經》的陳子畫等號,希望以後有新材料和新研究來解决這個問題。按《漢書·藝文志》,數術類有六種:“天文”以外,陰陽五行、五音、鐘律入“五行”、數學入“曆譜”(如《許商算數》二十六卷);疾病之類,已經不是“數術”文獻,而歸入“方技”。本篇簡文如按《藝文志》分類,當入數術類,但難以繼續划分小類。
簡文問答的内容偏重理論,而不談具體操作。例如,雖然提到“三方三圓”並爲之命名,却並没有像《周髀算經》那樣談到三衡及日至的測算方法;雖然提到身體疾病、土木工程等問題,也没有具體的測算。和已知的秦漢簡《日書》的日常實用性,更形成鮮明反差。然而,簡文將十二時、十日、五音、十二律、四卦都放在“三方三圓”的宇宙系統之中,不少地方都和秦簡《日書》、戰國秦漢“月令”文獻、天文學説密切相關,不僅是進一步探索戰國末年到漢初數學思想的重要材料,實際上也爲系統考察秦簡《日書》的理論基礎帶來新的刺激。
附記: 拙稿寫作過程中多次向彭浩老師請教,又承《簡帛》審稿專家提供參考資料,謹此一併致謝。

