建筑移动机械臂末端定位技术研究
宋 韬 ,荚启波 ,韦邦国 ,李沈阳 ,郭 帅
(1.上海大学 上海市智能制造及机器人重点实验室,上海 200444;2.上海机器人产业技术研究院,上海 200062)
0 引言
中商产业研究院预计,2018年建筑装饰行业市场规模将超过4.5万亿元,增长率达6.7%。随着收入水平的逐步提高,对生活空间环境的改善已经成为居民消费投入的主要方向[1]。建筑机器人作为一个具有极大发展潜力的新兴技术,有望实现“更安全、更高效、更绿色、更智能”的信息化营建,整个建筑业或借机完成跨越式发展。
二十世纪80年代初期,日本清水公司研制出的SSR-1喷涂机器人被认为是世界上首台用于施工的建筑机器人[2]。苏黎世联邦理工学院研制出In-situ Fabricator砌墙建筑机器人主要由履带式移动平台、6轴ABB机械臂和末端吸盘式执行器组成[3]。西班牙加泰罗尼亚先进建筑研究所提出来了MiniBuilders3D打印建筑机器人系统则包括三套3D打印机器人系统,分别用于基座、墙体和墙面的打印作业[4]。河北工业大学研制出幕墙安装机器人C-ROBOT-I,其由移动平台、升降机构、搬运机械臂及机械手,主要用于板材的干挂安装作业[5]。
目前,移动机械臂常用的定位方法有两种:相对定位和绝对定位。相对定位是通过测量机器人相对于起始位置的距离和方向来确定机器人的当前位置,包括惯性导航和测程法两种方法[6],其优点是无需感知外界环境,缺点是漂移误差会随时间累积逐渐增大,不适于精确定位。绝对定位分为图形匹配定位、GPS定位、路标定位等[7]。匹配定位方法的缺点是计算速度慢,计算结果不精确[8]。GPS适用于室外定位,而且定位精度较差。路标定位无需给定初始位姿即可得到机器人在任意位置的绝对位姿,无累积误差,定位精度高,但设计一种易识别的路标是关键。
本文针对建筑移动机械臂定位问题进行研究。首先,介绍了系统组成及其工作流程;然后,对定位系统进行分析,介绍了工作原理和定位算法;其次,对移动机械臂坐标系进行转换分析,求解出各坐标系之间的转换矩阵;最后,开展模拟环境下的作业实验,对定位精度进行测试。
1 移动机械臂系统及作业流程
基准线绘制是根据设计要求,在现场将墙体及家具的实际位置用墨线画出来,并按测量数据给予标注标记。上海大学设计开发了建筑移动机械臂MoMaCo,其包含全方位移动单元、定位单元、升降单元、机械臂单元、末端执行器等,系统组成如图1所示。
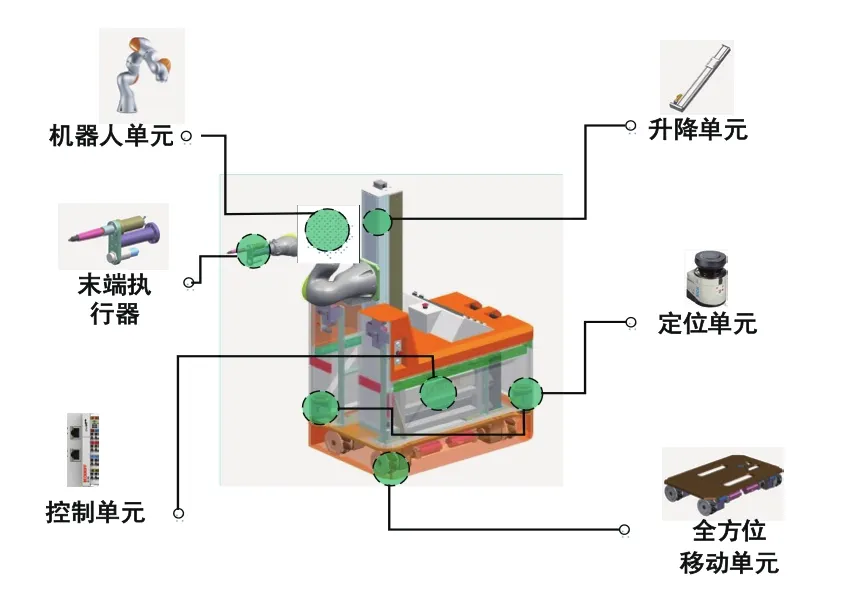
图1 建筑移动机械臂MoMaCo的组成
系统作业流程如下:
1)定位:两个激光测距传感器安装在移动平台的对角处,可实现360°范围的测距。将所测结果与预置于系统中的平面图进行对比,使用定位算法可确定移动平台的位置。
2)移动:上位机将位置信息和运动指令发给下位机,驱动机器人移动到指定位置。到达后,下位机发送完成信号。
3)重复上述步骤直至到达。
4)作业:定位后,系统规划路径后进行基准线绘制作业。工作流程如图2所示。

图2 移动机械臂工作流程图
2 基于环境特征的定位方法
装修作业多发生在室内环境中,系统定位可基于直线、直角等环境特征。定位流程如图3所示。

图3 定位流程
1)坐标转换:对传感器数据集进行预处理,式(1)将扫描数据点[ri,θi]从极坐标形式转换到直角坐标系下,得到:Rfi=[xi,yi]。

2)滤波:对传感器采集噪声进行处理,本研究采用中值滤波方法基于式(2)进行平滑处理。
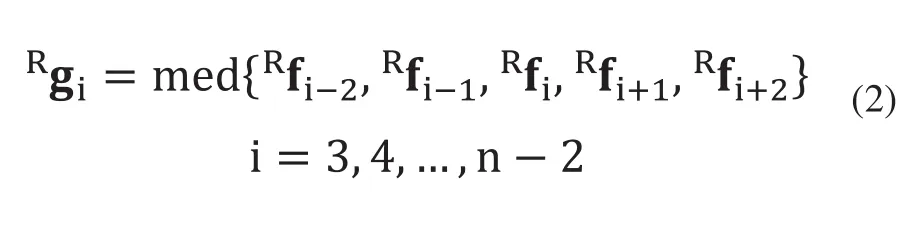
Rgi为滤波后得到的扫描坐标点数据。
3)自适应聚类:本文使用自适应聚类方法将描述同一对象的坐标点聚合在一起。计算相邻点的距离di,i+1,将其与预置的阈值ρ进行比较。

预置的阈值ρ是根据式(4)求得,该阈值与激光传感器的检测距离正相关:

其中,∆φ为激光传感器的角度分辨率,研究中取0.25°;λ为辅助常量参数,取λ=10°;σr是测量距离误差,取σr=0.01m。

4)直线分割:针对聚类后得到的点集,判断其几何特征,并将点集划分为若干直线。首先对点集进行初次直线拟合,同时计算该点集中所有点到拟合直线垂直距离的标准差σfit。同时,根据经验给定直线拟合阈值ift并进行比较。若σfit≤fit,则表明该类数据为直线。若σfit>fit,即表明聚类后的数据不满足直线判断标准。实际作业中,取fit=30mm。对于室内环境而言,聚类后的数据还可能是直角特征,需要对不满足直线标准的聚类再次进行直角判断及直线分割。判断方法如下:先取该类首尾点相连成一条直线,在该类数据中找到距离该直线最远的点,并在该点处将该类分为两个子类。再分别判断两个子类是否为直线。同时,计算两个拟合直线的倾斜角之差β,若εmin<|β|<εmax且fit,则将分类储存成两条直线;反之重复上述循环直到环境中有效直线提取完成结束。在实际作业中,取εmax=100°,εmin=80°。
5)直线拟合:使用最小二乘法对满足直线判断条件的点集进行直线拟合。假设该类中有n个数据点=[xk,yk],其中k∈[1,n]。
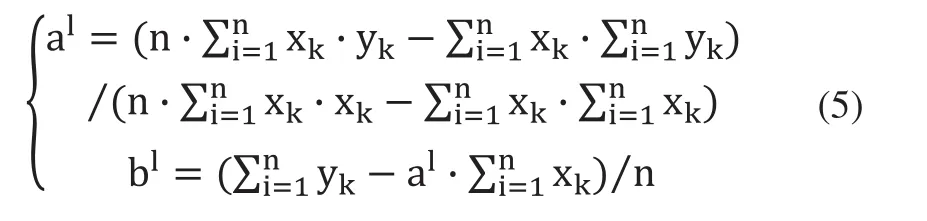
所得到的al为拟合直线的斜率,bl为拟合直线的截距。
6)环境特征点提取:环境特征点是指室内建筑的墙角处,在定位分析中是通过分析两条相邻直线之间的相交点来得到。若相邻两条直线的参数为(al,bl)、(al+1,bl+1),根据式(6)可得出相交点的坐标Rsl=[xl,l+1,yl,l+1]T。
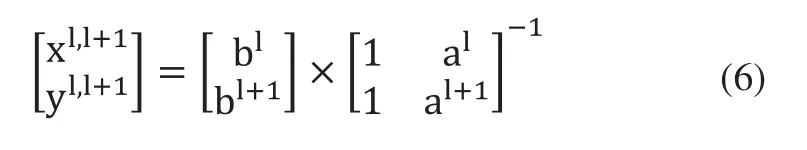
7)特征点匹配:步骤6中提取出的环境特征点是基于移动机械臂局部坐标系,需要经过特征点匹配进一步将其转换至全局坐标系{XGYGZG}下。取局部坐标系中特征点集RQl={Rsl-1,Rsl,Rsl+1},RQl中三个点形成一个三角形。根据平面几何相关理论,提取三角形的三个参数,最大内角αmax和组成最大内角的两条边的边长l1与l2,且令l1<l2。此时,针对存在三个特征点的特征点集RQl相对应的有[αmax,l1,l2]来描述其几何特性。特征点在全局坐标系下的位置是通过预置地图的方式已存入系统中,特征点匹配过程则是通过根据特征点之间所形成的几何特性的判定来进行匹配。具体的过程为:特征点在全局坐标系下的坐标点集和为GMPk={GMP1,GMP2,…,GMPp},p为特征点的个数。所以,这些特征点可组成个三角形,相对应的,存在个[αmax,l1,l2]。如图4所示,匹配的原则是根据三角形的全等的关系去匹配每个特征点的位置信息。计算αmax,l1,l2]与集合GQl中所对应三角形的[Gαmax,Gl1,Gl2]二者之间的差值,若以下三个条件同时满足,则认为匹配成功。此时Ql在全局坐标系下可记为GQl={Gsl-1,Gsl,Gsl+1}。
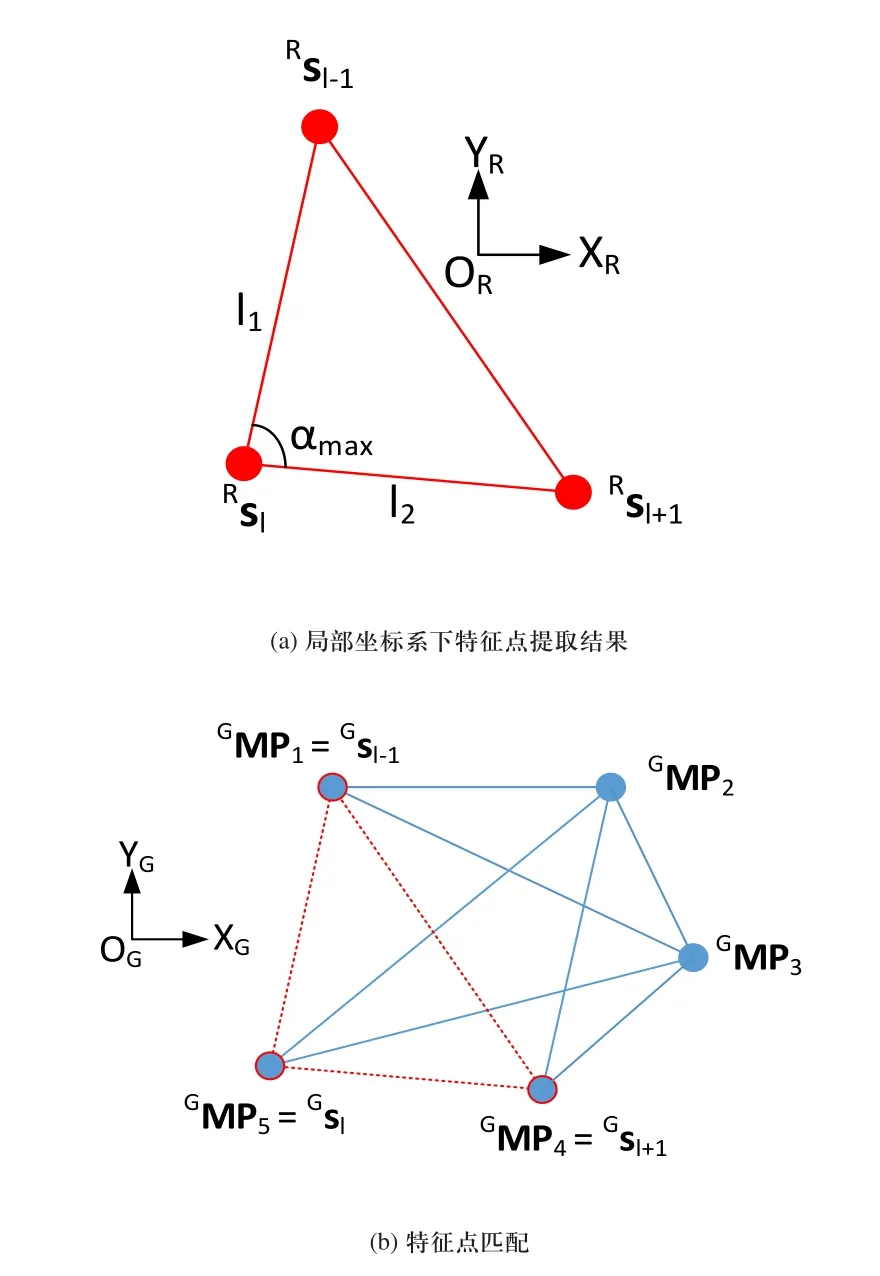
图4 特征点匹配
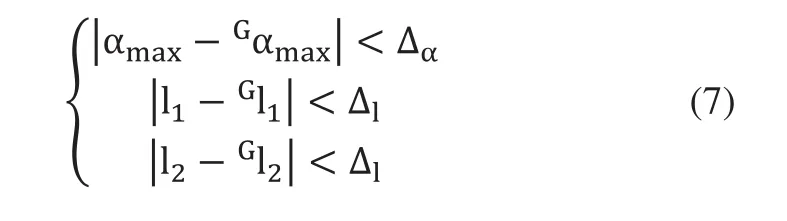
实际中,∆1=10°,∆2=25mm。
8)定位:定位中采用了三边法的几何原理。如图5所示,假设某一时刻,激光经过特征提取后得到特征点集合在全局坐标系下匹配出的特征点集合机器人相对于这三个点的相对距离ml-1、ml与ml+1可根据局部坐标系下特征点的位置求得。
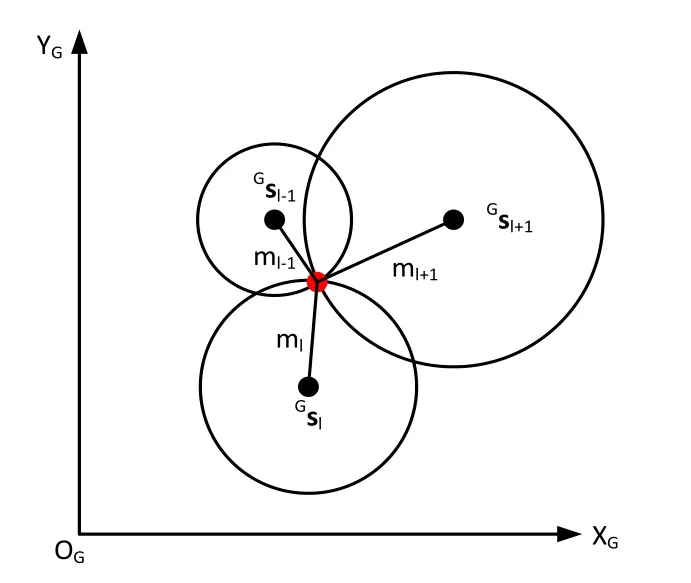
图5 三边定位原理图
假设机器人的位姿GP=[Gx,Gy,Gφ],且Gsl=(Gxl,Gyl),根据三边法得出下式:
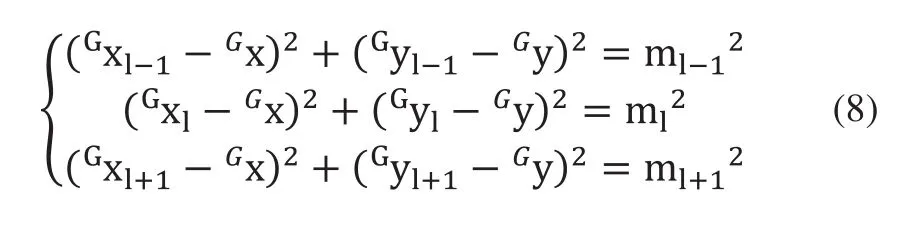
可得到机器人在全局坐标系下的位置:
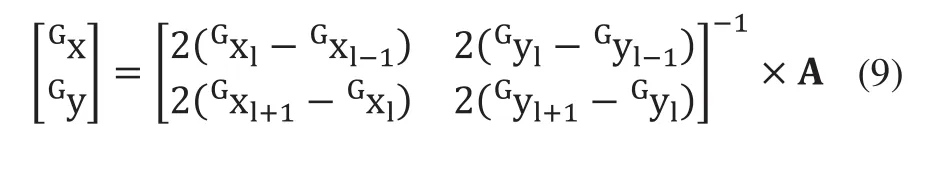
其中:

同时,求解航向角:

3 机械臂末端位姿的确定
根据上节可得到系统在全局坐标系下的位姿,而该系统在装饰画线工作时需要得到移动机械臂末端的位姿,因此需将机器人系统的位姿换算到机械臂末端。
3.1 机械臂模型构建
本文采用D-H方法来描述机械臂,机械臂坐标系如图6所示,D-H参数如表1所示。
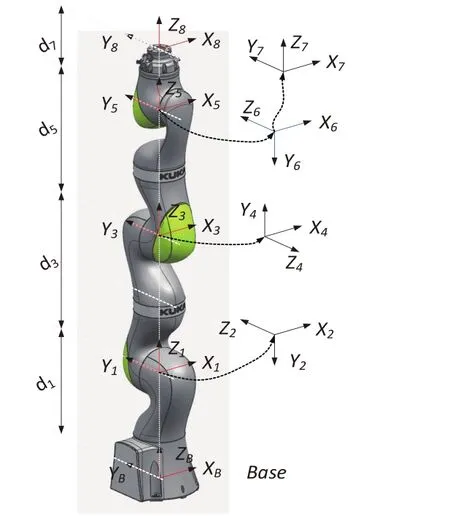
图6 机械臂坐标系

表1 机械臂DH参数值
运动学方程可表示为:

式(13)中:
θi为关节变量;
p为末端参考点相对于基坐标系的位置向量;
3.2 移动机械臂转换矩阵换算
要完成机械臂末端的定位,需要经过4个坐标系转换:全局坐标系{XGYGZG},移动平台中心坐标系{XRYRZR}、机械臂基座坐标系{XBYBZB}及机械臂末端坐标系{XTYTZT},机械臂基座坐标系{XBYBZB}与机械臂基座中心位置重合。因此,整个系统在环境中坐标系如图7所示。

图7 移动机械臂坐标系图
移动平台坐标系相对于全局坐标系的位姿建立在定位的基础上,通过定位算法可知建筑移动机械臂在全局环境中的位姿为GP=[Gx,Gy,Gθ],则移动平台坐标系相对于全局坐标系的变化矩阵为:


由移动机械臂设计可知:l1=402.5mm,l2=38.5mm,h是升降平台的高度参数。
机械臂末端坐标系相对于机械臂基座坐标系的转换关系与机械臂的连杆坐标系相关,则:

最后,根据以上的转换矩阵可知机械臂末端坐标系在全局坐标系下的转换矩阵为:
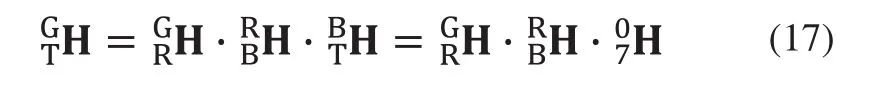
4 实验验证
如图8所示,为了测试定位精度,搭建了模拟实验环境,编制了定位软件。软件界面如图8右上角所示,其中机器人周围的各种颜色直线是基于定位算法得到的环境特征。
开展了建筑移动机械臂基准线绘制试验,测量施工放线相对于基准线之间的距离差值,与建筑装饰行业放线精度相比较。施工作业质量评定结果表明:移动机械臂基准线绘制作业的位置与角度误差满足建筑装饰行业放线精度要求。
5 结束语
本文针对建筑移动机械臂在空间环境中机械臂末端定位问题进行了分析与研究。首先,搭建建筑移动机械臂的整体系统框架,并对其工作流程进行详细的阐述;其次,对系统中的定位系统进行研究分析,介绍了定位的工作原理以及三边定位的算法;之后,对移动机械臂坐标系进行转换分析,求解出各坐标系之间的转换矩阵。最后,开展了移动机械臂的精度测量实验。实验结果表明:移动机械臂末端定位精度满足建筑装饰行业放线精度要求。这为后续移动机械臂在复杂环境中定位控制奠定基础,更为日后复杂环境中定位技术提供了平台和借鉴。

