基于MBD的检测路径规划方法研究

屈力刚，胡宝慧，李 亮

（1.沈阳航空航天大学 机电工程学院，沈阳 110136；2.中航工业中国空空导弹研究院，洛阳 471000）

0 引言

MBD的定义是指基于模型的信息定义技术，基于MBD建立的全三维环境不但能够提高检测效率还可以确保检测结果的正确性，将三维实体模型导入三坐标测量机辅助软件中，可以实现离线路径规划。检测路径规划是数字化检测中一道关键步骤，它对检测效率的影响起到绝对性作用。在现场进行实际检测操作中，三坐标测量机测头角度的频繁变换以及路径的长短都会影响到检测的精度和效率，如果只考虑路径的长短而忽视三坐标测头角度的频频变更，那么得到的不一定是最佳测量路径，说明路径规划其实是一个测头方向和路径距离的组合优化问题[1]。国内外有很多学者对路径规划进行了研究，Requicha[2]采用贪婪式聚类算法，对检测点进行检测方向分集，直至所有检测点都明确了各自的检测方向；纪小刚[3]等人将最短路径距离为核心思想，提出用遗传算法来完成路径的优化；曾德标[4]等人对模拟退火算法进行了完善，优化选择了测头检测方向等。本文提出通过K-means算法与余弦相似度结合，将同一个测头位姿下测点划分集合，由于构造一个特征的所有点都能够在同一个测头位姿下检测，所以在进行测头位姿规划中只需要知道每一个特征向量的测头位姿方向即可，实现在路径规划过程中降低工作量提高检测效率。蚁群算法[5]是一种仿生算法，该算法是通过蚂蚁在找食过程中的行为提出来的，它可以在行走的路径上产生有利出种族内通信的激素，在最短路径上的蚂蚁来往频率往往多于其他路径上的蚂蚁，原因是最短路径上留下的通信激素多容易被其他蚂蚁发现并效仿。因此本文采用蚁群算法对得到的测头位姿集进行集内和集间测量点间路径优化。

1 测头位姿规划

1.1 可达性测头位姿

一般对于测头位姿来说，要保证所有待检测点都能进行检测，尽量规避检测过程中产生干涉和碰撞，选择一个合理的测头位姿有利于对接下来路径规划提供方便。可达性测头位姿是指三坐标测量机测头虚拟成在检测点无限延长的一条射线，并且与测头位姿方向相反。在检测过程中，测头没有和零件产生摩擦碰撞，所形成射线的方向就是这个检测点的可达位姿。根据前面的原理介绍，我们能够获得某个检测点的全部可达位姿的射线，并且它们最终都会汇集到一个锥空间中，也就是说我们能够知道每一个检测点的可达测头位姿。最后把获得的全部可达位姿集合进行求交运算，这样能够减少重复测头位姿从而降低个数。

设p是检测点，n是检测点在零件上的外法矢，l是测针的轴线方向，n和l之间的角度为（n，l）。值得注意的是，测头位姿方向需要和这个检测点法线之间形成的角度不大于90°，即（n，l）≤90°，若超过这个范围即是不可达测头位姿。检测点聚类通常可以用可达性锥原理来完成，它须要按照测头转动最低刻度来把所有点可达性锥进行离散进而获得可达位姿。三坐标测量机可以保证的测量方向为有限和离散[6]，接下来令全部检测点的可达位姿通过求交运算一一分析其可达性。在本文研究中，水平面内转动角度即水平角设定为A，竖直平面内摆动角度即垂直角设定为B，测头的检测方向为水平角和垂直角的组合（A，B），A和B都有最低转动刻度值，由于采用的测头转动最低刻度为15°，即每一个检测点可达性锥都能够组合离散出特别多的可达位姿，便会造成接下来求交计算量异常复杂，因此本文选择以下算法去完成检测点的聚类。

图1 点P的可达测头位姿原理图

1.2 测头位姿选择

关于传统K-means算法已有的缺陷，许多人提出了改善办法，但在本文中并不适用，深入研究提出了余弦相似度与K-means结合的优化算法。通过衡量两个特征向量之间的法向夹角的相似性叫做余弦相似度[7]，如果余弦相似度为1，那么这两个特征的方向是一样的；如果余弦相似度是0，两个向量的方向是垂直的；所以余弦相似度范围在0-1区间，且无限接近于1两个特征方向无限接近；然后通过K-means算法将方向无限接近的特征聚类划分，即可在同一个测头位姿下测量。

有数据集包含了n个特征对象的数据集合，并且每一个特征对象都有m维特征属性，sil（i=1，2，3，…，n；l=1，2，3，…，m）那么代表第i个代表对象的第l维属性。特征对象si与sj的余弦相似度为：

对特征方向进行相似度衡量，首先对属性进行标准化处理，避免不同属性量纲对结果造成偏差的影响，标准化后属性s*il的公式为：公式中max(sil)指l维属性中最大值，min(sil)指l是维属性中最小值。

图2 余弦相似度示意图

K-means聚类流程：

1）任意选择k个聚类数目，并将选择的这k个特征对象作为初始的聚类中心。

2）求出每一个特征向量和这k个聚类中心点的余弦相似度，同中心点相似度最接近的特征向量会被划分到当前类别里。

3）重新求得每一个类别中新的聚类中心点，将每一个类别中全部特征对象的平均值定义为新的中心点，前后进行比较，如果中心点不变那么算法结束，中心点改变将返回第一步。

但是在这个算法中，首先要确定k的取值。

图3 K-means聚类原理示意图

为此本文将引用类内内聚度和类间分离度两个概念，因为最大化类内内聚度和类间分离度能够使聚类效果较好。而轮廓系数方法[8]，可以同时包含内内聚度和类间分离度。

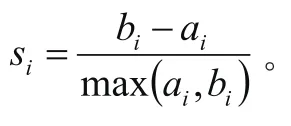
2 测量路径规划

2.1 集合内路径规划Inpathi

为各个测头位姿下的集合内部路径规划Inpathi，流程如下所示：

在一个集合内随机选取为该路径的起始点和pote为终止点，添加前一个测头位姿集合内终点areai-1和下一个测头位姿下起始点areai+1采用最近邻法求出集合内路径。

重复第一步，但要注意的是，随机选取点时跳过已选点不能重复选取，对形成的所有路径作比较，选择最短路径。

将这个集合内的起止点与选取最短路径集合内的起止点保持一致，目的是为了使求出来的局部最优路径能够，在全局路径规划中也可以保持较优。

当测头和零件不产生碰撞时，两个检测点之间距离disij便是两点之间的路径长度。但在实际操作中，不能不考虑检测精度，所以在检测路径中必须添加靠近和回退路径badis。

最终用公式表示为:

图4 集内顺序规划流程图

2.2 集合间路径规划Outpathi,i+1

求解集合间最短路径，可以归类于TSP问题，在本文研究中将各个集合的几何中心点投影到一个平面上，这样就可以形成以往TSP问题中的一个节点，将投影到固定平面的所有节点，构造一个二维点阵，然后采用蚁群算法对形成的二维点阵路径进行优化。蚁群算法实现的主要步骤如下：

1）把路径信息原始化，设置蚂蚁个数为m，节点个数为n。

2）蚂蚁k在经过每一个节点时都要按照概率来进行选择下一个要访问的节点，那么在t时蚂蚁k从节点i选择到节点j的概率为：

allowed=（0，1，2，…，n-1）为蚂蚁k还没有到达的节点，即接下来可选取的节点。α为通信启发因子，β为期望启发因子，为蚂蚁k在t时间i与j之间遗留的通信激素量，为i与j之间距离启发程度。

3）求出每一只蚂蚁的预期函数值，找到并记录目前最佳值。

4）蚂蚁在t时间内结束一次轮回，各列轨迹上通信激素量调整原则为下：

公式中，ρ为轨迹持久性，1-ρ为信息残余因子，为k只蚂蚁在这次轮回中残余在i与j之间路径上的通信激素量。

5）令n=n+1，对i与j之间路径，设置为∆τij=0。

6）当n＜节点数，则转到第2步；否则结束。

通过以上算法进行仿真实验，在零件模型上取点得到图5(a)集间二维点阵的路径，未经蚁群算法优化前，距离为839.8297；蚁群算法优化后的路径距离为519.9644，如图5(b)所示；经蚁群算法优化路径自然顺畅，测点路径上缩短为原来的61.91%。

图5 集合间路径优化效果图

3 结论

将零件模型导入三坐标测量机软件中，选取了几组特征进行现场离线路径规划，图6(a)所示为未使用本文提出的算法路径图，图6(b)所示为规划后的路径图，通过表1能够看出本文研究的算法可以得出较优的检测路径和较少的检测时间，极大地提高了检测效率，在离线路径规划中避免了测头损坏等损失。

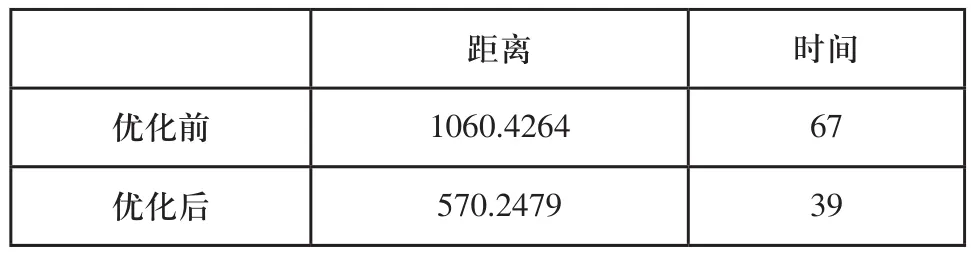
表1 优化路径前后对比表

图6 使用三坐标测量机现场检测路径图