基于3D视觉的高精度加工件测量研究
(河南理工大学 电气学院,焦作 454150)
0 引言
随着图像处理技术和视觉计算技术在工业自动化生产中的快速发展,基于机器视觉引导的量测技术已经在当今的工业生产中占据了举足轻重的位置。进入二十一世纪以来,2D视觉测量方法已经远远不能满足工业生产的需求,对于一些高精度同时具有特殊的量测位置的产品也让传统的视觉检测方法显得式束手无策,因此基于3D视觉的测量技术受到研究者的广泛关注,同时得到了快速发展。机器视觉算法的效果严重依赖于输入图像得质量,表面缺陷检测、深度测量、共面性检测、曲面度检测等均是3D视觉技术得优势。针对这些检测方式2D相机想要取得一幅质量好的图像非常困难,3D激光测量技术的出现弥补了传统视觉量测技术的缺陷,为空间3D信息的获取提供了全新的技术手段,为信息数字化发展提供了必要的生存条件[1]。
汽车发动机是汽车的心脏,为汽车提供动力,发动机的正常运行是汽车安全行驶的保障。汽车发动机由很多种零件组装而成,在零件生产过程中,大或小的零部件的不良都会直接影响到汽车正常行驶过程中发动机的安全,危害驾驶员的生命安全,因此对发动机的零部件实现快速而精确的测量尤为重要。本文对汽车的一种核心零件的进行高精度测量研究,针对测量部位是产品表面的凹陷深度提出了一种基于3D视觉的高精度加工件测量系统。陈方[2]提出了3D测头和宏程序相结合一体式3D机床自动测量的方案,该技术价格相对比较昂贵,精度不稳定,自适应性差。安宗权[3]等人提出了一种基于线激光的工件平面平坦度的测量,该方法采用平面均值算法,对产品底面水平度依赖性比较强,当产品不是绝对水平时精度会下降。
为了解决当前3D视觉测量技术对凹陷深度测量精度不佳的问题,本文提出了基于最小二乘法Huber法拟合空间平面算法,该算法以点到面的距离为研究方向,通过以产品表面为基准面,寻找凹陷最低点,最低点到基准面的距离就是真实的凹陷深度。该方法不会受到底面倾斜等因素的干扰,并且成本低廉,精度高,稳定性强。本文通过组织架构、硬件部分、软件部分、现场结果与分析四大部分进行研究,加工件良品的凹陷深度范围为1.45±0.15mm,精度要求为小于0.02mm,从精度可以看出测量本身存在一定的难度,对研究具有很大的意义和价值。
1 3D视觉检测系统整体结构
本文的3D视觉系统分为2D视觉和3D视觉两大部分。其中2D视觉部分的流程为:2D上相机定位和模板匹配得出旋转角度并返回给上位机角度信号,上位机控制机构并旋转产品,2D侧相机测量产品的高度和宽度,同时3D相机采图并通过算法测量出产品表面的凹陷深度返回给下位机OK或NG信号并保存数据,下位机根据返回的信号做出判断,对产品进行分类回收。3D视觉系统整体工作流程图如图1所示。2D视觉的作用不仅可以保证3D相机每次取到的图像角度不会有太大的变化,同时可以减少小部分3D视觉测量算法的时间。本文研究的重点为3D视觉系统部分。
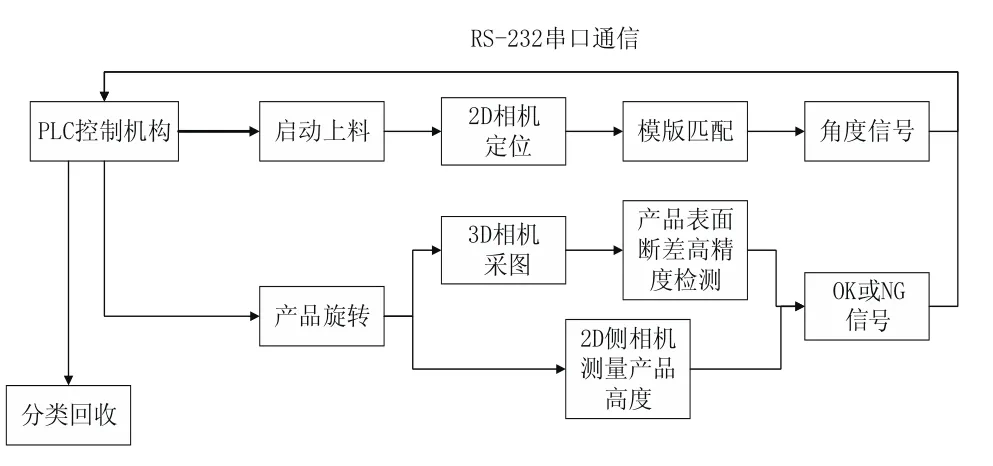
图1 3D视觉系统整体工作流程
3D视觉系统是从摄像机获取的图像出发,计算三维环境物体的位置、形状等几何信息,并由此重建和识别环境中的物体。线激光光源中的几何信息帮助提取景物中的几何信息,利用光平面照射在物体表面产生光条纹,在拍摄的图像中检测出这些条纹,它们的形态和间断性,构成了物体各可见表面与相机之间的相对测度[4,5]。通俗的讲就是激光照射到3D物体表面,因为物体表面是存在高度变化的,导致激光线发生弯曲,通过传送带带动物体运动,多条激光曲线拼接在一起就形成物体表面的轮廓[6]。实验测试平台如图2所示。

图2 实验测试平台
2 硬件部分
2.1 测量对象

图3 3D视觉测量对象
本次研究的3D视觉测量对象如图3所示。产品为一个直径约40mm的圆盘,测量位置1、2、3处凹坑的深度。考虑到2D相机所用的光源为红色面光源,打光方式为背光源频闪方式,整个流程速度比较快,蓝色线激光会受到红光干扰造成3D相机扫描取像不准确。为了避免红光对蓝色线激光的干扰,经过计算与分析,3D视觉图像的选取的视野应比测量对象的长度大一些,图像的视野大小规定为50×50mm。2D相机进行产品尺寸测量时,3D相机扫描的起点并没有在产品上,干扰可以降到最低。
2.2 3D视觉系统硬件部分
3D视觉系统硬件主要由:3D相机、线激光、镜头、电源线、通信线、标定板等部分组成。3D相机采用Sick-RangerE50相机,分辨率为1536×512像素,3D相机电源为24V直流电源;镜头采用Schneider Makro-IRIS/C MOUNT的40mm C口镜头;激光采用2M级,20mW/450nm/10度发散角(Z-Laser);RS-232通信连接线;点阵标定板;一台工业工控机。相机与激光架设采用三角测量架设方式,采集硬件架构图如图4所示,激光采用蓝色激光,垂直照射。3D相机与线激光光束方向夹角α的最佳角度范围为30°~50°,本次实验取α=30°。点阵标定板如图5所示,斜面角度为16°。各硬件部分通过成本、精度等严格的计算之后进行选型,通过选型后搭建测试平台比一体式3D采集器要廉价。
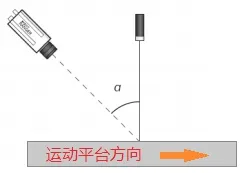
图4 采集硬件架构图

图5 点阵标定板
3 软件部分
3D视觉系统软件主要采用HALCON11.0软件和Visual Studio2012软件混合编写。HALCON11.0软件具有强大算法库,3D视觉系统的显示界面由Visual Studio2012软件C#开发平台进行编写,该软件同时负责与PLC的通讯、数据结果汇总等。Ranger Studio软件负责3D相机标定。
软件部分可以进行数据处理,通过3D相机采集到的图像信息,生成产品空间X-Y-Z三个方向的数据点云信息。通过3维坐标与“点云”信息构建产品得立体轮廓信息,对2D平面离散点通过最小二乘法算法拟合成一条直线进行改进,采用最小二乘法Huber方法把整个3维空间离散的点拟合为一个理想化空间平面,最终计算出产品表面任意兴趣点到拟合之后空间平面的距离就等于产品表面任意兴趣点处的凹陷深度。
3D系统逻辑架构如图6所示,待测产品随着传送带运动至测量起点位置,激光感应装置感应到产品,启动激光,同时回传给PLC信号,PLC发出+5V上升沿信号触发3D相机采集数据,产品移动50mm(视野大小)后,激光关闭,3D相机停止数据采集。
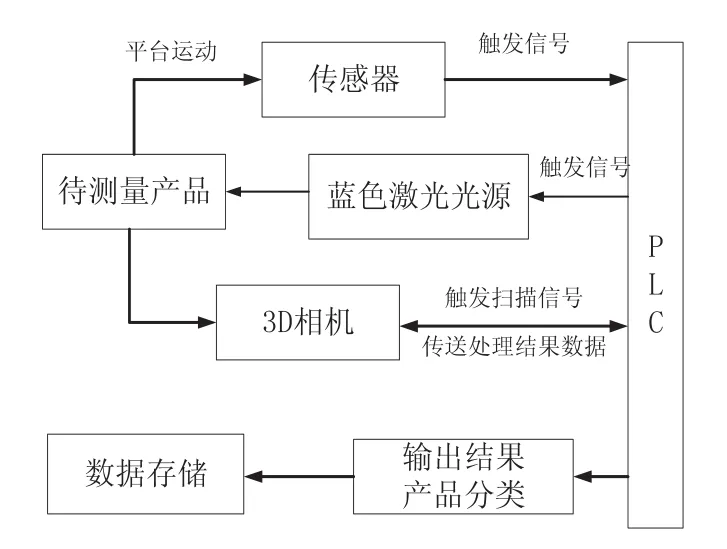
图6 3D系统逻辑架构图
标定是视觉测量的关键环节,标定精度直接影响对工件的测量精度[7]。2D图像标定一般采用2D平面靶面标定法[8],2D图像坐标系只有X-Y方向。3D相机标定的原理是通过保持空间坐标X-Y方向不变,Z方向坐标数据转换为2D图像的灰度值,通俗的讲就是空间坐标系X-Y-Z(高度)转变为2维平面坐标系X-Y-灰度值。3D相机标定时首先设置扫描起始行和行的数量,让标定板扫描后的图像充满视野,其中任意相邻两个点的水平距离为△X=3.5mm,垂直方向距离△Z=△X×sin16°=0.965mm。通过亚像素边缘提取后再椭圆拟合或利用灰度质心法等,能够较容易地得到圆(椭圆)中心亚像素精度提取。参数导入Ranger Studio后标定的图像如图7所示,图7(a)为标定前的标定板图像,图7(b)为标定之后的标定板图像。图像由高度图像转换为未格式化的图像数据,并且图像数据按像素连续地填充,并逐行逐行地填充。标定之后空间的X方向分辨率为0.026mm,Y方向分辨率为0.016mm,Z方向分辨率为0.006368mm。

图7 标定板标定前后图像对比图
标定完成后采用HALCON11.0的算法库读取数据文件。采用算子read_sequence(:Image:HeaderSize,SourceWidth,SourceHeight,SourceWidth,SourceHeight,StartRow,StartColumn,DestWidth,DestHeight,PixelType,BitOrder,ByteOrder,Pad,Index,FileName:)读取像素类型为“real”的数据文件。其算子参数如图8所示,其中参数Source Width为3D相机X方向分辨率为1536pixels,参数SourceHeight为扫描行数666行,SourceHeight=Y方向移动距离/Y分辨率,Y分辨率=传送带速度*循环采集时间。图8中红色箭头指示为“点云”图像数据存放的路径。

图8 算子参数
采用算子threshold(Image,Region,1,255)和reduce_domain(Image,Region,Reduced)算子对图像进行处理,得到“real”型图像。3D相机采集到的3D图像和“real”型图像如图9所示。
传送带速度过快采集到的图像容易失真,速度过慢会影响工作效率,经过分析与计算,激光启动时设置传送带的最佳速度为匀速15mm/s,整个运动过程为上料后先加速,激光扫描时匀速,收到处理结果后再加速。标定后的图像如图10所示,从图10中可以清楚的看到经过标定后图像灰度值数值从Int型变换为Double型,灰度值的单位为mm。经过标定之后真实深度值=产品基准平面平均灰度值-凹陷区域最低点灰度值。图10中可以看出采集到的图像中有很多噪声,这些噪声会对最后的精度造成干扰,中值滤波算子median_image(Image:ImageMedian:MaskType,Radius,Margin :)能够有效抑制噪声,可以很好的过滤掉椒盐噪声,可以得到高质量的图像。

图9 3D图像与“real”型图像

图10 标定后的图像
中值滤波后的图像如图11所示。图像噪声处理之后分两大部分进行:1)寻找产品表面三个位置凹陷处的最低点;2)寻找与产品最低点相对应的基准平面。经过大量数据分析,这两个部分具有紧密的联系,凹陷处最低点和基准平面选择的准确性,直接影响最后测量值的精度。

图11 中值滤波后的图像
寻找产品表面最低点的方法如下:采用阈值分割(二值化)算子threshold(Image:Region:MinGray,MaxGray :)。经过阈值分割后可以得到产品表面三个凹陷区域,对三个区域进行开运算、闭运算和腐蚀处理,进一步去除干扰。最后用感兴趣区域筛选算子select_shape(Regions,SelectedRegions:Features,Operation,Min,Max:)得到的三个稳定的区域,接着对三个兴趣区域进行排序,用For循环对每个区域进行单独处理。算子min_max_gray( )和gray_features( )得到凹陷区域(region)的最小灰度值Min和凹陷区域的最小灰色值特性Value,然后取参数Difference_Value:=Min-Value,算子Threshold(Image,EndRegion,Value,Value+Difference_Value/2)对凹陷区域进行阈值分割,把凹陷区域最低点筛选出来。运用此算法流程可以筛选掉图像中干扰,保证算法得到最低点具有极高的稳定性和准确性。
基准平面选取的合理性同样影响最后测量的精度。寻找基准平面:陈方提出的平面均值测量算法采用二值化算法和兴趣区域筛选算法得到产品上表面区域,以筛选出的区域为基准面,利用的算子intensity(Regions,Image::Mean,Deviation)求出平面灰度值的平均值Mean。高度差=Mean-最低点灰度值Min。经过大量的实验测试以及对测量数据进行统计分析得:这种方法的前提条件是工件底座需要保证绝对水平,然而在实际生产中零件底面不可能绝对水平,底面是存在误差的,并且加工件在3D扫描运输过程中会发生轻微抖动造成加工件倾斜,运送平台与产品底面不是绝对平行的,平台允许存在0.01mm的机械误差。以上多种因素的累加影响,使得测量精度远超出了0.02mm的精度要求。

图12 产品柱形底座多角度立体图
在二维平面内对一些离散的点,可以通过采用最小二乘法方法把这些离散的点拟合成一条直线。经过深入的算法研究与学习发现,在三维空间内也可以实现运用最小二乘法把离散的空间点拟合为一个空间平面,点到拟合面的距离就是真实的高度差,并且这个高度差不会因为受到产品倾斜等因素的干扰而变化。如图12所示为产品柱形底座多角度立体图,红色区域为产品柱形底座上表面拟合成的基准平面,黑色圆点为表面凹处最低点,h为最低点到平面的距离,从图中可以看出高度h不会因为产品的倾斜而变化,精度比较高。
通过标定和新的视觉算法把产品表面所有点的坐标(x,y,灰度值)拟合为一个平面,分别计算出产品表面三个最低点到拟合基准平面的三个距离,这三个距离就是加工件表面三个凹坑的深度h。
采用Huber[9]法对平面进行抗差最小二乘法拟合估计。采用抗差估计最小二乘法Huber法,可以降低离群值的影响[10],可以对测量进行等价权处理,与传统的最小二乘法相比,当测量的数据存在误差,Huber法可以得到更精确的估计结果。
三维空间加权最小二乘法拟合平面算子采用fit_surface_first_order(Regions,Image:Algorithm,Iterations,ClippingFactor:Alpha,Beta,Gamma)。Regions为需要拟合的区域,Image为3D相机采到的图像,Algorithm参数选择′Huber′,采用加权最小二乘法拟合平面。Iterations为最大的迭代次数;ClippingFactor为消除异常值的剪辑因子;Alpha为近似曲面的参数α;Beta为近似曲面的参数β;Gamma为近似曲面的参数γ。算子的参数公式如式(1)所示,点到面的距离D如式(2)所示。假设需要求点(x0,y0)到某平面的距离,式(1)中变量r_center为拟合区域中心X方向坐标;变量c_center为拟合区域中心Y方向坐标;r和c分别为式(2)中的x0和y0;Image(r,c)等于式(2)z0;z0为点(x0,y0)处灰度值;式(1)展为一般式如式(3)所示。

由式(1)~式(3)得:

由式(4)可得:

通过式(5)可以求出产品表面任意凹陷处最低点到产品表面的距离,相对应的最小二乘法(Huber法)拟合空间平面算法如图13所示。

图13 最小二乘法(Huber法)拟合空间平面算法
4 项目测试结果
HALCON与Visual Studio2012配合时候需要用到HALCON的算法函数创建功能。自定义创建HALCON函数库,把主要的算法写入自定义得函数库中,这样做的优点是:在HALCON转C#格式的之后,我们在界面程序编写的时候可以直接引用这些函数库来处理,可以减少检测时间,同时可以保证HALCON算法稳定的运行。如图14所示是HALCON主要算法及运行结果,算法处理时间t仅为0.015S,封装后的算法(最终形式)及运行结果如图15所示。

图14 主要算法及检测结果

图15 最终的算法形式及测量结果
本次研究采用高度规测量、平面均值算法和最小二乘法Huber拟合空间平面算法三种方法对随机挑选出的5个产品分别进行100次的重复测量,对测量数据进行深度分析,比较三种方法测量出的最大值与最小值的差值验证三种算法的精度及稳定性。表1为采用高度规对5个产品三个凹陷位置测量100次的精度结果,表2为采用平面均值法对5个产品三个凹陷位置测量100次的精度结果,表3为采用最小二乘法Huber拟合空间平面算法对5个产品三个凹陷位置测量100次的精度结果。由表1、表2和表3可知高度规测量方法随着测量次数的增多,人工测量精度会越差,最大精度0.048mm。平面均值算法在平台旋转、倾斜等干扰下最大精度为0.03mm,超过了0.02mm。最小二乘法Huber拟合空间平面算法最稳定,不会因为测量次数的增多导致精度下降、精度不受平台旋转、倾斜等因素的影响,精度可以达到0.01mm。
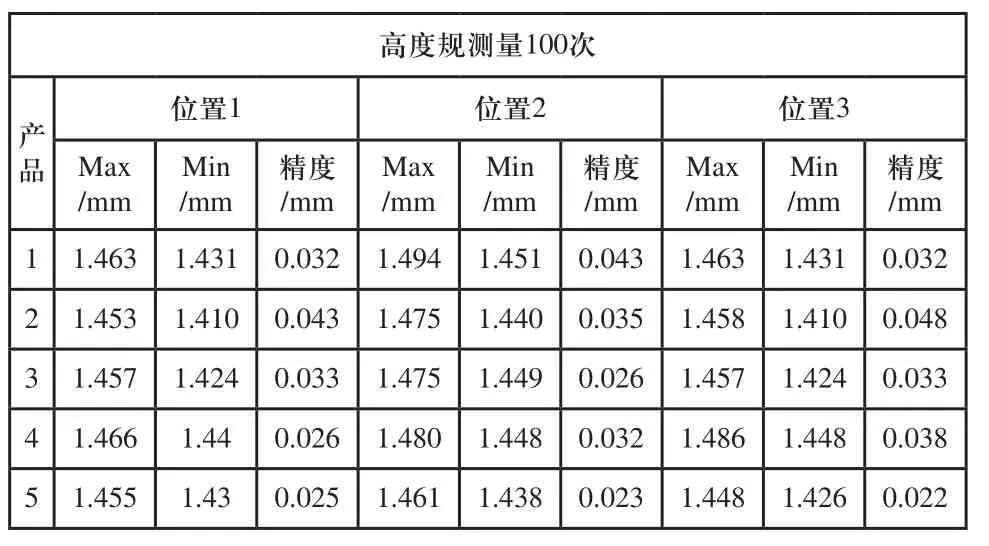
表1 高度规对5个产品三个凹陷位置测量100次的精度结果
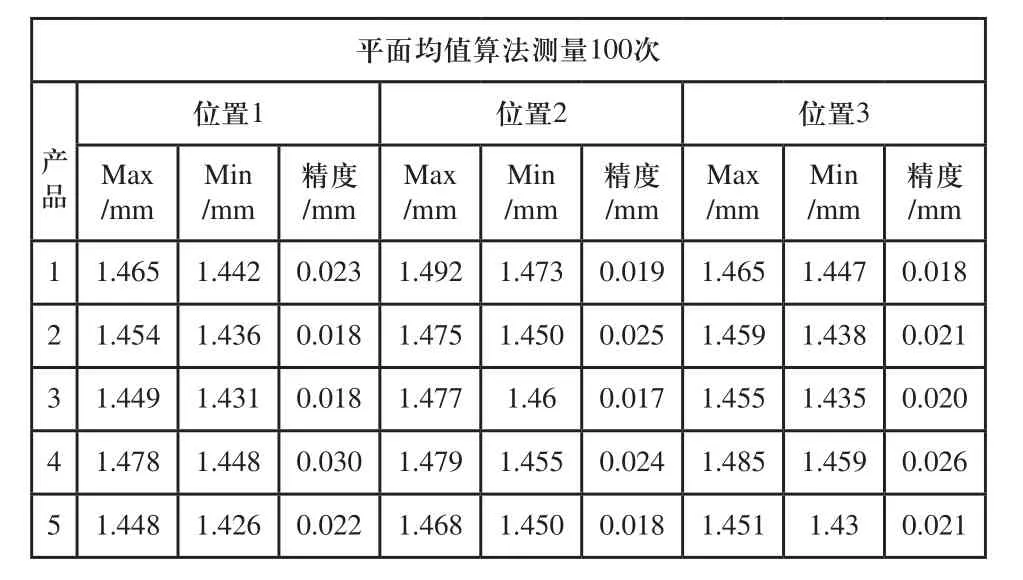
表2 平面均值法对5个产品三个凹陷位置测量100次的精度结果

表3 Huber拟合空间平面算法对5个产品三个凹陷位置测量100次的精度结果
图16为对产品1的三个凹陷位置重复测量100次,验证采用Huber拟合空间平面算法的测量重复精度曲线图,通过图16中三个曲线的最大值和最小值的差值可以验证测量的重复精度,如图16所示,凹陷位置Point1处测量的重复精度为0.00995mm。凹陷位置Point2处测量的重复精度为0.00903mm,凹陷位置Point3处测量的重复精度为0.00831mm,三处凹陷位置综合测量精度达到了0.01mm。图17为用户正常运行UI界面。
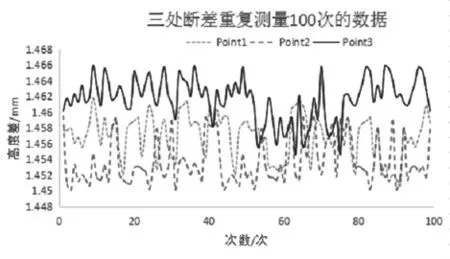
图16 验证Huber拟合空间平面算法测量的重复精度曲线图

图17 用户正常运行UI界面
5 结束语
本文提出的3D视觉测量系统已成功应用于生产线。通过生产过程中大量的数据验证,本系统具有运行稳定、精度高、可靠性强的优点。通过最小二乘法Huber拟合空间平面算法,测量精度达到了0.01mm,速度仅为0.02s。新算法以测量三个凹陷位置深度为例,还可适用于产品表面多处凹陷深度的测量、产品共面性程度的检测、产品曲面度的检测等等。实验结果表明:本文研究的最小二乘法Huber拟合空间平面算法与传统技术相比有更好的测量效果。

