基于抛物线模型拟合的三波束比幅测角
李 敬,张 琛
(中国船舶重工集团公司第七二三研究所, 江苏 扬州 225101)
0 引 言
相控阵雷达是雷达信号处理技术、新型器件与计算机技术结合后发展到高阶段的产物,是随着电子计算机和微波移相技术的发展而诞生的。雷达探测的重要任务之一就是探测目标位置,目标测向是目标位置参数估计中的重要研究内容,因相控阵天线具有波束扫描的快速性、灵活性与波束形状的捷变能力,其在波束形成上是多种多样的,测向方法也不尽相同。相控阵雷达一般采用同时多波束进行目标探测,为了测量目标的精确方位,必须采用相应的方法利用这些多波束进行方位估计。本文针对三波束同时接收的工作方式介绍一种高精度测角方法,即利用抛物线模型拟合实现三波束比幅测角。
1 天线方向图
比幅法测角是利用天线收到的回波信号幅度值来做角度测量的,该幅度值的变化规律取决于天线方向图以及天线收发方式。本文所介绍的工作方式是:发射一个宽波束,采用3个相同且彼此部分重叠的波束同时接收的方式[1],接收示意图见图1。
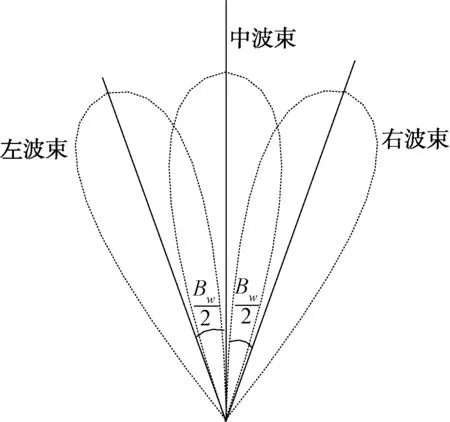
图1 三波束接收示意图
图1中左、中、右3个波束同时接收目标回波,Bw为半功率波束宽度,三波束彼此重叠的角度为Bw/2。图2是1路发射波束3路接收波束的方向图。图中黑实线表示指向为法线方向(0°)的发射波束,虚线依次从左到右分别表示3 dB波束宽度为Bw的接收波束的左(波束1)、中(波束2)、右(波束3)三波束。
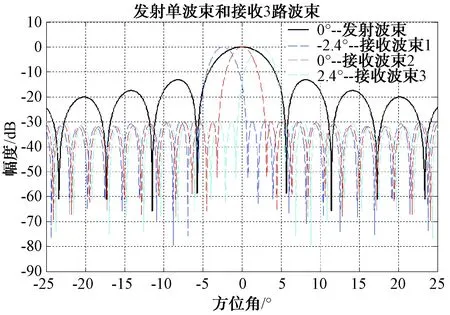
图2 发射波束和3路接收波束方向图
2 三波束比幅测角
三波束同时接收的目标回波,在幅度上有一定的对应关系,即目标靠近哪个接收波束,哪个波束的回波幅度就大,且回波幅度最大的位置就是目标所在位置,为此可以利用开口向下的抛物线函数y=ax2+c进行三波束目标回波幅度的函数拟合,求出目标所在的具体方位。如图3所示,该抛物线以y轴为对称轴,x轴表示中心波束指向偏离目标的角度偏差,y轴表示回波幅度。
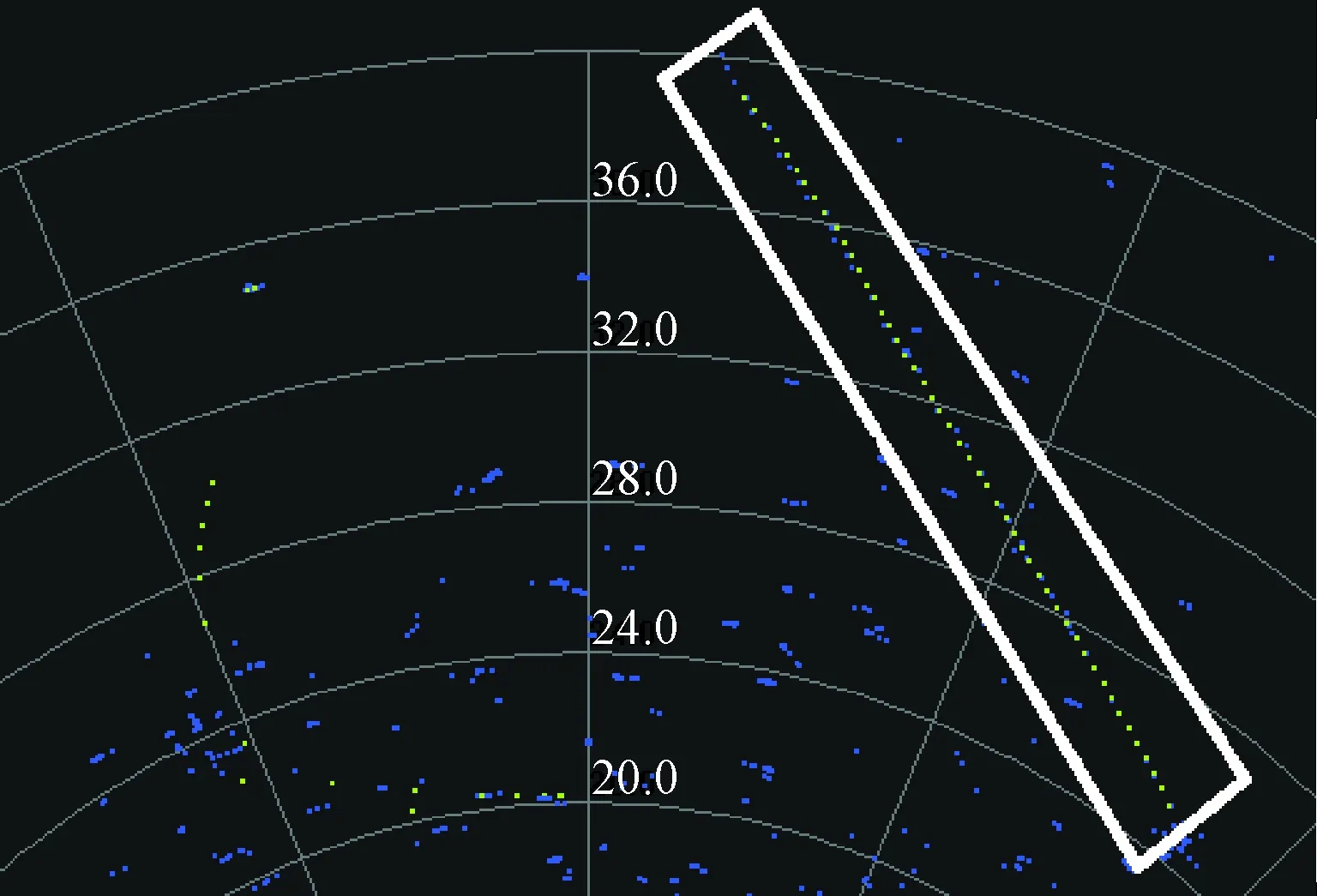
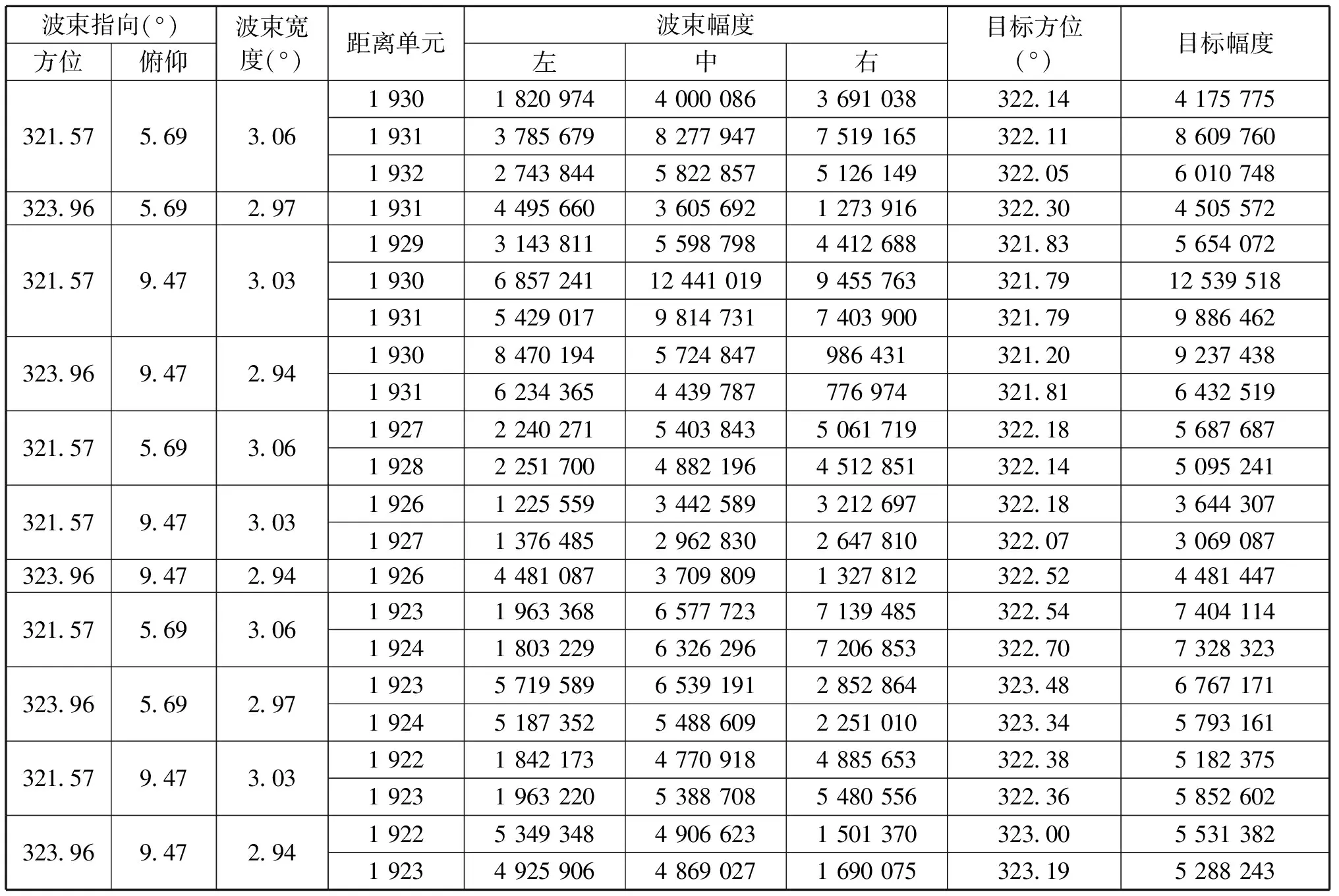
设左、中、右三波束测得的目标参数为(xlyl)、(xcyc)和(xryr)。xl,xc和xr分别为左、中、右三波束的方位指向,yl,yc和yr分别为三波束测得的目标回波幅度。如果目标位于中心波束,不考虑副瓣影响,理论上左右两波束幅度值相等,分别位于抛物线的两边。此时xc=0表示中心波束指向目标,目标幅度最大值c=yc落在y轴上。当目标偏向左波束,位于中心波束和左波束之间时,回波幅度的最大值已不是中心波束上测得的回波幅度值了,则中心波束指向xc≠0。如图3所示,xc代表了目标偏离中心波束的角度偏差。此时目标指向的回波幅度仍然是最大,仍然位于抛物线最高点,最大值仍然是c,即目标最大幅度永远位于y轴上。由此设目标在抛物线上的参数为(xpyp),xp>0,yc 图3 抛物线拟合实现三波束比幅测角 将左、中、右三波束测得的目标参数(xlyl)、(xcyc)和(xryr)代入抛物线模型得: (1) 若三波束之间两两夹角为波束宽度的一半,即Bw/2,则有: (2) 将公式(2)代入公式(1)求得: (3) 从公式(3)可知yl,yc和yr分别为三波束测得的目标回波幅度,为已知值,Bw为接收波束宽度,也是已知的,由此可求得拟合参数a和c,该抛物线就确定了。同时还可求得目标角度修正值xc。相控阵雷达在工作的时候,波束指向是确定的,将波束指向用xc值修正后就可得出目标的真方位和回波幅度。 抛物线模型拟合实现三波束比幅测角的验证是通过在设备上测量民航机来验证的,见图4。图4中的点是民航机在不同波位上的视频回波,为了方便显示,在每个波位上只绘出中心波束的回波视频,框内是民航机的回波视频。通过采用抛物线模型拟合实现求每组波束目标的位置后,再进行点迹凝聚和航迹处理,实现对目标的稳定跟踪,与ADS-B数据对比,试验测得方位跟踪精度均方根小于0.3°。 图4 民航机回波视频 图5是对回波数据进行比幅测角,求目标方位和俯仰、视频凝聚后的点迹数据,框内是民航机的点迹数据。从图5可以看出,民航机在整个飞行过程是均匀飞行的。表1是对应图4框内视频回波的数值,图4中显示的是地理坐标系下目标的位置,表1中对应的是阵面坐标系下目标的位置,阵面架设参数方位-45°,倾斜角20°,比幅测角数据最终要从阵面坐标转换到地理坐标系下[2]。 图5 民航机点迹与航迹 由于数据量比较大,只给出了3个扫描周期的视频数据及对应的参数,每个粗框内对应着一个扫描周期的视频回波,每个周期大约有3~4个波位的立体角内可以探测到目标。每个粗框内的数据可以凝聚成图5中的一个点。每个波位对应大约2~3个距离单元,每个距离单元对应目标左、中、右(如图1所示的)3个回波波束的幅度值,目标幅度和方位分别是对左、中、右三波束进行抛物线拟合实现三波束比幅测角得到的目标方位值和该方位对应的目标幅度值。 表1 民航机三波束视频回波 文献[3]中的映射内插法虽然也采用抛物线模型,但是用了y=ax2+bx+c模型,而工程中已知的只有3个波束的幅值和波束间隔,在解算目标方位时,少一个已知量,因此添加了一个约束条件α=-b/2a,这就导致函数的不灵活性,而本文巧妙地将目标位置移至y轴上,这样就变成了y=ax2+c模型,既满足了已知参数,又不加任何约束,可以根据已知参数,拟合最佳抛物线系数,对于多波束(大于3个接收波束)也可采用此方法。 利用抛物线拟合实现三波束比幅测向不需要进行繁琐的定标,处理简单,且由相控阵雷达原理知,随着阵列扫描方位的变化,发射波束和接收波束会相应展宽,即Bw随着天线扫描角度变化而展宽,因此随着角度变化抛物线形状是变化的,该方法可以充分利用3对测量数据进行抛物线拟合求得a和c,从而求出目标指向。同时该算法还可以求得目标的幅度参数,如果设备的稳定性好,幅度参数作为后续数据处理会是一个很重要的参数,可以为后续杂波图积累和航迹关联提供依据。 必须注意的是比幅测角要求同一时刻测得的目标才能进行比幅,如果对某个运动目标扫描时不连续,是无法进行比幅测角的,目标可能跨多个距离单元。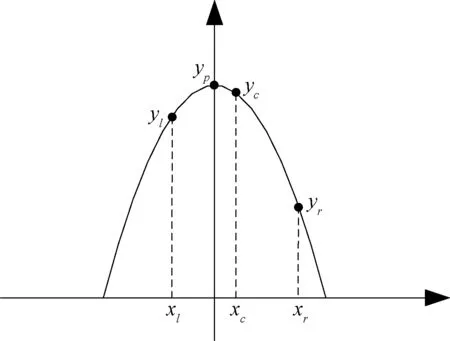
3 数据验证与结论

4 结束语

