L-fuzzy凸子群度及其诱导的L-fuzzy凸结构

韩元良, 张晓瑾, 文小艳

(华北科技学院 理学院, 河北 廊坊 065201)

1971年,Rosenfeld[1]介绍了模糊群的概念.1979年,Anthony等[2]重新定义了模糊群.从此,群论中很多经典的结论陆续被推广到模糊群中.除了研究模糊群的性质之外,一些学者还研究了模糊子群与它们水平集之间的关系.Dixit等[3]借助水平集给出模糊共轭子群的刻画.Shi等[4]借助水平集给出L-fuzzy子群度及L-fuzzy正规子群度的刻画.同时,近些年对L-fuzzy凸结构的研究成果[5-8]也较为丰富.然而,对L-fuzzy凸子群及L-fuzzy凸子群度的研究成果几乎还没有.

基于此,本文一方面给出L-fuzzy凸子群和L-fuzzy凸子群度的定义,并借助不同形式的水平集刻画它.另一方面,借助L-fuzzy凸子群度诱导一种新的L-fuzzy凸结构.

1 预备知识

文中L表示完全分配格,其最大元和最小元分别记为┯和┷.M(L)表示L中所有非零并既约元之集,P(L)表示L中所有非单位素元之集.对∀a∈L,由文献[9]中知a恒有最大极小集和最大极大集,分别记为β(a)和α(a),且β和α分别为保并映射和保交并映射.设X为非空集,LX表示X上的全体L-集,对∀A∈LX,a∈L,沿用文献[10]中的符号,有如下4种形式的水平集:

A[a]={x∈X|A(x)≥a},

A(a)={x∈X|A(x)≤/a},

A(a)={x∈X|a∈β(A(x))},

A[a]={x∈X|a∉(A(x))}.

有关水平集的诸多性质可参考文献[4,9].

设X为非空集,LX表示X上的全体L-集[11],L和M均是完全分配格,┯M代表M的最大元.定义1.2给出了X上的(L,M)-fuzzy凸结构的定义.

定义1.2[8]称映射C:LX→M为(L,M)-fuzzy凸结构,若满足以下条件：

(LMC1) C(χ)=C(χX)=┯M;

(LMC2) 若{Ai:i∈Ω}⊆LX非空,则

(LMC3) 若{Ai:i∈Ω}⊆LX是非空全序集,则

称(X,C)为(L,M)-fuzzy凸空间,又称(L,L)-fuzzy凸结构为L-fuzzy凸结构.

定义1.3[1]设L是完全分配格,A是群G的L-fuzzy子集.若对∀x,y∈G满足

A(xy-1)≥A(x)∧A(y),

则称A是G的L-fuzzy子群.

2 L-fuzzy凸子群度及其诱导的凸结构

首先给出L-fuzzy凸子群和L-fuzzy凸子群度的定义,借助4种形式的水平集对其进行等价刻画,最后由L-fuzzy凸子群度诱导出一种新的L-fuzzy凸结构.首先,给出L-fuzzy的凸子群的定义.

定义2.1设L是完全分配格,A是群G的L-fuzzy子集.若对∀x,y∈G满足

A(xy-1)≥A(x)∧A(y),

A(λx+(1-λ)y)≥A(x)∧A(y),

则称A是G的L-fuzzy凸子群.

接下来,借助完全分配格上的剩余蕴涵算子给出L-fuzzy凸子群度的定义,也即是说,定义每个子集A是G的凸子群的程度.

定义2.2设A是群G的L-fuzzy子集,则A的凸子群度m(A)可定义如下：

A(λx+(1-λ)y),0<λ<1).

由定义2.2容易得到引理2.3.

引理2.3设A是群G的L-fuzzy子集,则m(A)≥a当且仅当

∀x,y∈G,A(x)∧A(y)∧a≤A(xy-1)∧

A(λx+(1-λ)y), 0<λ<1.

基于引理2.3,容易得到L-fuzzy凸子群度的等价定义如下.

定理2.4设A是群G的L-fuzzy子集,则

m(A)=∨{a∈L:A(x)∧A(y)∧a≤A(xy-1)∧

A(λx+(1-λ)y),0<λ<1,∀x,y∈G}.

接下来,借助4种不同形式水平集给出L-fuzzy凸子群度的4种等价刻画形式.

定理2.5设A是群G的L-fuzzy子集,则

m(A)=∨{a∈L:∀b≤a,A[b]是G的凸子群}.

证明设对∀x,y∈G,

A(x)∧A(y)∧a≤A(xy-1)∧A(λx+(1-λ)y),

即

A(x)∧A(y)∧a≤A(xy-1),

且

A(x)∧A(y)∧a≤A(λx+(1-λ)y),

则对∀b≤a及∀x,y∈A[b],有

A(xy-1)≥A(x)∧A(y)∧a≥b∧a≥b,

A(λx+(1-λ)y)≥A(x)∧A(y)∧a≥b.

这表明xy-1∈A[b],λx+(1-λ)y∈A[b].因此,A[b]是G的凸子群.

反过来,设a∈L及∀b≤a,A[a]是G的凸子群.对∀x,y∈G,设b=A(x)∧A(y)∧a,则b≤a且x,y∈A[b],因此xy-1∈A[b]且λx+(1-λ)y∈A[b],即

A(xy-1)≥b=A(x)∧A(y)∧a,

A(λx+(1-λ)y)≥b=A(x)∧A(y)∧a.

综上即证结论成立.

定理2.6设A是群G的L-fuzzy子集,则

m(A)=∨{a∈L:∀b∉α(a),A[b]是G的凸子群}.

证明设对∀x,y∈G,

A(x)∧A(y)∧a≤A(xy-1)∧A(λx+(1-λ)y),

则对∀b∉α(a)及x,y∈A[b],有

b∉α(A(x))∪α(A(y))∪α(a)=α(A(x)∧A(y)∧a).

由

A(x)∧A(y)∧a≤A(xy-1),

A(x)∧A(y)∧a≤A(λx+(1-λ)y),

可得

α(A(xy-1))⊆α(A(x)∧A(y)∧a),

且

α(λx+(1-λ)y)⊆α(A(x)∧A(y)∧a).

因此b∉α(A(xy-1))且b∉α(λx+(1-λ)y),即

xy-1∈A[b],λx+(1-λ)y∈A[b].

从而,A[b]是G的凸子群.

反过来,设a∈L,∀b∉α(a),A[b]是G的凸子群.假定b∉α(A(x)∧A(y)∧a),由

α(A(x)∧A(y)∧a)=α(A(x))∪α(A(y))∪α(a),

可知b∉α(a)且x,y∈A[b].因为A[b]是G的凸子群,所以xy-1∈A[b],λx+(1-λ)y∈A[b]成立,即b∉α(A(xy-1))且b∉α(A(λx+(1-λ)y)),从而A(x)∧A(y)∧a≤A(xy-1)且A(x)∧A(y)∧a≤A(λx+(1-λ)y).综上即证结论成立.

定理2.7设A是群G的L-fuzzy子集,若满足β(a∧b)=β(a)∩β(b),则

m(A)=∨{a∈L:∀b∈P(L),b≥/a,A(b)是G的凸子群}.

证明设对∀x,y∈G,

A(x)∧A(y)∧a≤A(xy-1)∧A(λx+(1-λ)y).

设b∈P(L),b≥/a及x,y∈A(b).下面证明xy-1∈A(b),λx+(1-λ)y∈A(b)成立.若xy-1∉A(b),即A(xy-1)≤b,则有A(x)∧A(y)∧a≤b,因此a≤b,这与b≥/a矛盾.因此xy-1∈A(b).同理可证λx+(1-λ)y∈A(b).这表明A(b)是G的凸子群.

反过来,设a∈L,∀b∈P(L),b≥/a,A(b)是G的凸子群,只需证明对∀x,y∈G,

A(x)∧A(y)∧a≤A(xy-1)∧A(λx+(1-λ)y).

设b∈P(L),A(x)∧A(y)∧a≤/b,则A(x)≤/b,A(y)≤/b,a≤/b,即x,y∈A(b).由于A(b)是G的凸子群,则xy-1∈A(b)且λx+(1-λ)y∈A(b),即A(xy-1)≤/b且A(λx+(1-λ)y)≤/b.这表明

A(x)∧A(y)∧a≤A(xy-1),

A(x)∧A(y)∧a≤A(λx+(1-λ)y).

综上即证结论成立.

定理2.8设A是群G的L-fuzzy子集,则

m(A)=∨{a∈L:∀b∈β(a),A(b)是G的凸子群}.

证明类似上述定理容易证明.

基于群同态和L-fuzzy凸子群度的定义,可以得到L-fuzzy凸子群度的性质定理.

定理2.9设f:G→G′是群同态,

1) 若A是G的L-fuzzy子集,则

2) 若A是G的L-fuzzy子集且f是单射,则

3) 若B是G′的L-fuzzy子集,则

4) 若B是G′的L-fuzzy子集且f是满射,则

证明1) 由定理2.4可得

∨{a∈L:A(x)∧A(y)∧a≤

A(z)∧A(w),x,y∈G}=m(A).

2) 因为f是单射,由定理2.3可得

∨{a∈L:A(x)∧A(y)∧a≤A(xy-1)∧

A(λx+(1-λ)y),x,y∈G}=m(A).

B(f(x)f(y-1))∧B(f(λx+(1-λ)y)))≥

B(λx′+(1-λ)y′))=m(B).

4) 由于f是满射,借助1)可得

最后,借助L-fuzzy子集A的凸子群度m(A)诱导出一个新的L-fuzzy凸结构,也即是说,m可以看作LG到L的一个映射,由下面的定理可知映射m诱导群G上的一个L-fuzzy凸结构.

定理2.10设A是群G的L-fuzzy子集,m(A)是A的L-fuzzy凸子群度,则映射m是G上的一个L-fuzzy凸结构.

证明(LMC1) 显然,m(χ)=m(χG)=┯.

(LMC2) 设{Ai:i∈Ω}⊆LX是非空集,需证

Ai(x)∧Ai(y)∧a≤Ai(xy-1)∧Ai(λx+(1-λ)y),

从而

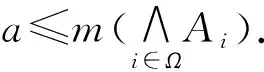
(LMC3) 设{Ai:i∈Ω}⊆LX是非空全序集,需证

Ai(x)∧Ai(y)∧a≤Ai(xy-1)∧Ai(λx+(1-λ)y).

假定b∈J(L)且b则存在i,j∈Ω使得b≤Ai(x),b≤Ai(y)且b≤a.由于{Ai:i∈Ω}是全序集,假设Aj≤Ai,则

b≤Ai(x)∧Ai(y)∧a≤Ai(xy-1)∧Ai(λx+(1-λ)y),

从而

这表明