离散Leslie-Gower食物链模型的动力学行为研究
苏倩倩
(郑州成功财经学院通识教育中心,河南郑州 451200)
1 引言
Leslie-Gower作为一个重要的生态系统模型,已经引起了许多学者的关注,并且得到了很多好的结果(见文献[1–12]及所引文献).但是,对于生命短,世代不重叠的种群或者虽然生命长,世代重叠的种群在其数量少的时候,用差分方程(离散的动力模型)来表示更为合理(见文献[13]).鉴于此,本文将研究如下离散的Leslie-Gower模型
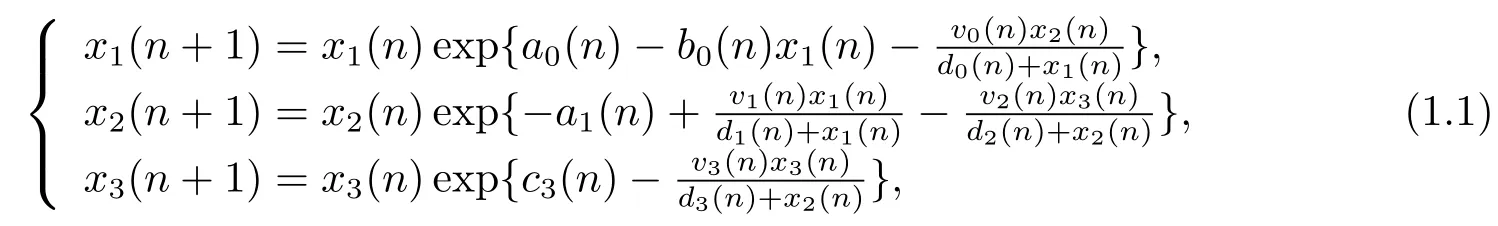
其中xi(n)(i=1,2,3)为种群i在n时刻的密度,a0,b0,v0,d0,a1,v1,d1,v2,d2,c3,v3和d3均为连续的有正的上下界的序列,且xi(0)≥0(i=1,2,3).
文[2]对离散两种群Leslie-Gower模型的周期解和全局吸引性进行了研究,而文[3]首次提出了一类连续的三种群Leslie-Gower模型.一个自然而然的问题是:离散三维Leslie-Gower模型的动力学行为又将怎样呢?据笔者所知,至今尚未有学者研究离散三维Leslie-Gower模型.本文参照文[14]的分析手法来研究系统(1.1)的动力学行为.更多有关Leslie-Gower模型的背景可以参考文献[3].这里对任意的序列{a(n)},记au=.
2 引理
引理2.1[15]假设序列{x(k)}满足x(k)>0,a(k)和b(k)为有正的上下界的非负序列,若x(k+1)≤x(k)exp{a(k)−b(k)x(k)},k∈N,则
引理2.2[16]假设序列{x(k)}满足x(k)>0,a(k)和b(k)为有正的上下界的非负序列,若x(k+1)≥x(k)exp{a(k)−b(k)x(k)},k≥N0,x(N0)>0,其中N0∈N,且,则

3 持久性与全局吸引性
定理3.1若

成立,则种群x1与x3持久,而种群x2绝灭.
证设x(n)=(x1(n),x2(n),x3(n))T为系统(1.1)的任意正解.由系统(1.1)的第一个方程得
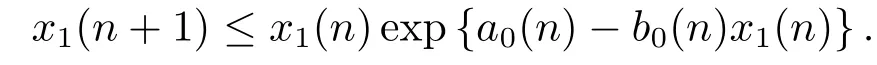
由引理2.1,得到
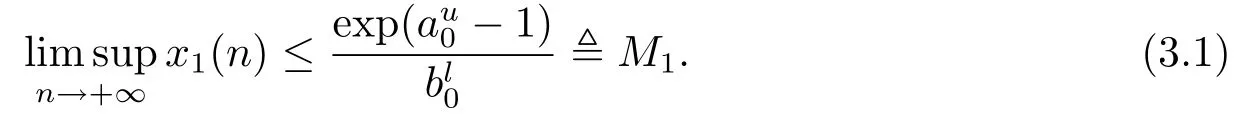
由系统(1.1)的第二个方程可得

由条件(H1)知

所以对于足够小的ε>0,存在N1>0,N1∈N,对任意n>N1,都有

由系统(1.1)的第三个方程得

由引理2.1知
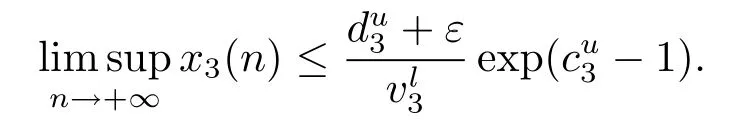
令ε→0得

则对于上述ε>0,存在N2>N1,N2∈N,对任意n>N2,都有

所以
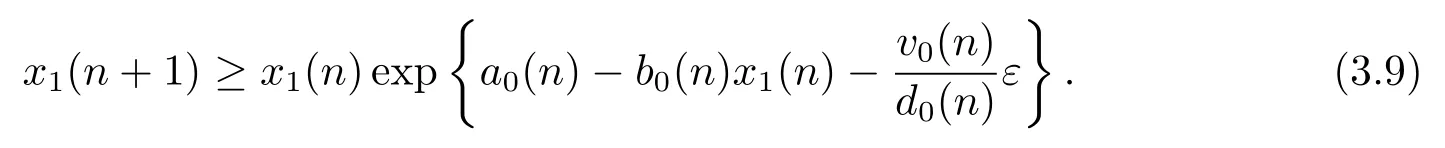
因为ε足够小,所以仍为正序列.则由引理2.2知

令ε→0得

由系统(1.1)的第三个方程得

由引理2.2知

下证M1>m1.
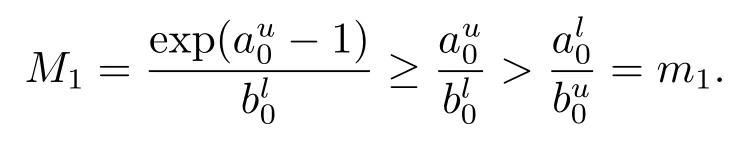


综上所述M1>m1,同理可以证明M3>m3.定理3.1证毕.
定理3.2假设(H1)成立,且

则系统(1.1)是全局吸引的.
证设为系统(1.1)的任意两个正解.因为,由定理3.1知,则.所以对于上述的ε>0,存在N3>N2,N3∈N,对于任意的n>N3,都有


当n>N3时,有m1−ε≤ξ1(n)≤M1+ε.则由(3.13),(3.14)式知

令ε→0 得|u(n+1)|≤λ1|u(n)|.因此,所以

当n>N3时,有

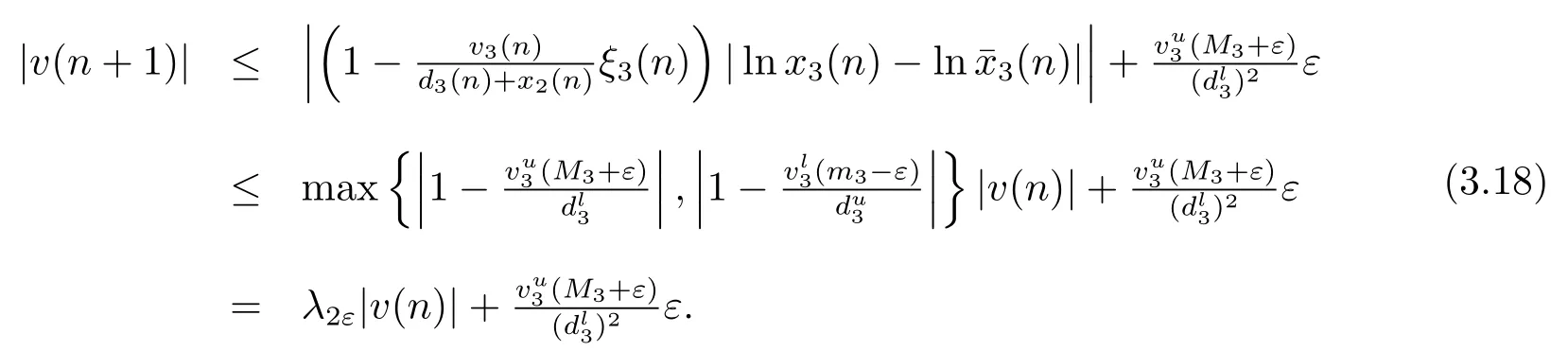
令ε→0 得|v(n+1)|≤λ2|v(n)|.因此,所以

定理3.2证毕.
4 数值模拟
例4.1考虑下面的系统

对应于系统(1.1),计算可知

满足定理3.1和定理3.2的条件,下面给出系统(4.1)的模拟图像.

图1:具有初始条件(x1(n),x2(n),x3(n))T=(0.62,0.60,0.65)T,(0.7,0.72,0.45)T,(0.45,0.5,0.75)T系统(4.1)的动力学行为
5 结论
本文研究了一类离散Leslie-Gower三维食物链模型,首先运用差分不等式的有关结论得到:若(H1)成立,则种群x1,x3持久x2绝灭,即当中级捕食者x2的死亡率大于食饵x1的人均减少率的最大值时,高级捕食者x3和食饵x1持久生存,而中级捕食者x2将走向绝灭.其次,通过采用文[14]的手法,构造适当的差分Lyapunov函数,得到了该系统全局吸引的充分性条件.文[2]研究了离散两种群Leslie-Gower模型的周期解和全局吸引性,文[3]首次提出并研究了一类连续的三种群Leslie-Gower模型,证明了该系统的有界性,吸引集的存在性,以及表示高级或中级捕食者灭绝的均衡的局部或全局稳定性.但文[17]指出,文[3]中关于有界解和不变吸引集的结论是错误的.所以对于连续模型的动力学行为还有待进一步研究.本文是在文[3,17]的基础上研究了离散三种群Leslie-Gower模型,是对文[2]的补充和完善.最后,数值模拟说明结论是可行的.

