非线性发展方程的无网格比高精度有限元方法
石东洋,王俊俊
(1.郑州大学数学与统计学院,河南郑州 450001)(2.平顶山学院数学与统计学院,河南平顶山 467000)
1 前言
众所周知,非线性发展方程的解通常无法直接用解析式写出来,或是写出来的表达式非常复杂,所以利用数值方法给出其近似解就显得尤为重要.而对于有限元方法这一主流方向,我们常见的线性化BE(Backward-Euler)方法和CN(Crank-Nicolson)方法凭借可以避免在每一个时间层都要求解非线性方程的劣势且不降低计算精度的优势,成为了该方向的研究热点之一.事实上,研究一个非线性发展方程的线性化有限元方法总会涉及到一个有限元解关于某种模的有界性问题,由于这些模的先验估计不容易直接得到,通常的处理技巧就是利用逆不等式.比如在二维的情况下,考虑有限元解有界时的经典做法是
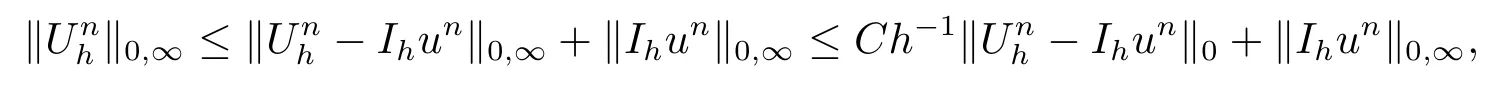
其中un是原始问题的解,Ih是某个插值算子或者投影算子.由于通常有误差估计(m1,m2为某些正数),要使有界就不可避免的要对时间步长τ有一个限制,从而导致空间网格参数h与时间步长τ需要满足某个比值关系(即网格比).在实际计算中,这样的网格比经常会导致时间步长变的非常小,从而引起很长的耗时.因此,怎样甩掉这些限制就成了备受关注的课题.最近,为了克服这一严重缺陷,孙伟伟、李步扬、王冀鲁、高华东等学者都在此方面做出了许多有价值的工作.其主要思想(见文献[1])是通过引入一个时间离散方程系统,并利用其解Un把误差分裂成两部分——时间误差un−Un和空间误差,利用时间误差的结果得到关于时间离散方程解的正则性,再利用空间误差得到有限元解的无网格比有界性事实上,由于空间误差的分析过程中甩掉了经典误差估计中的截断误差项,只要空间上的误差能写成(m3,m4为某些正数)的形式,网格比即可去掉.随后,王冀鲁、高华东、司志勇等又把该思想应用于非线性多孔介质流问题[2,3],非线性的Joule Heating方程[4],非线性Thermistor方程[5,6],非线性Schrdinger方程[7,8]和非线性Navier-Stokes方程[9]等.以上研究都考虑了这些非线性发展方程在协调元下关于无网格比的收敛性,有许多问题需要进行更深层次的研究.
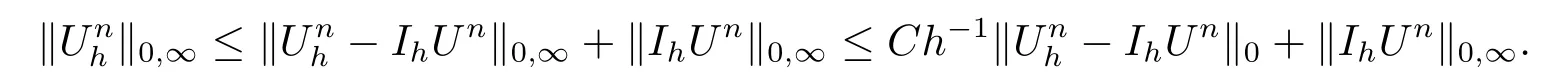
首先,为了提高有限元解的逼近精度,超收敛的思想已成为了一个重要的研究途径.事实上,在理论分析和实际计算中,若有好的网格,有限元解与有限元插值的误差在某种范数的意义下比有限元解与真解的误差要小得多,即超逼近现象.从上个世纪80年代开始,以林群院士为代表的众多学者专家都在此方面取得了许多有出色的成果,所以如何将无网格比收敛的结果推广到无网格比超收敛上去是我们感兴趣的话题.但是,为了达到超收敛的结果,如果我们把文献[1–9]中所考虑的区域换成更具一般性的矩形区域(不再满足C2的条件),则由椭圆的正则性可以看到,引入的时间离散方程解的有界性就很难达到H3-模.因此,如何在时间离散方程解的有界性较弱的前提下,探讨无网格比的超逼近结果就显得尤为重要.
其次,由于非协调元方法在大多数情况下对方程解的正则性要求比较低,因此人们对非协调元的研究一直保持着较高的热度(见以石钟慈院士为代表的众多学者专家所得到的具有特色的工作).这样就很有必要研究怎样利用自由度少、精度高的低阶非协调单元研究非线性发展方程的无网格比的超收敛性.
再次,传统的有限元方法对解的光滑度要求都比较高,这会给实际计算造成很多困难,因此混合有限元方法受到了高度的关注.事实上,混合有限元方法的关键性问题在于如何构造出合适的空间对,使其满足LBB条件,这其实是不容易做到的.因此构造特别的格式来降低LBB条件的难度成为了一个热点,比如:文献[10–13]对二阶椭圆问题提出了一种混合元格式,它具有当两个逼近空间满足一个简单的包含关系时,LBB条件容易满足且能避勉因涉及散度算子带来的麻烦等优点.另一方面,直接绕开LBB稳定性条件(如最小二乘法、稳定化有限元方法等)也成为了大家另一个关注的方面.事实上,1998年,Pani在文献[14]中提出了一种称之为H1-Galerkin混合有限元方法.这种方法不需要所选取的混合元空间满足LBB相容性条件,并被广泛应用在各种方程上.例如,长波方程[15],双曲方程[16],带有记忆项的方程[17],积分微分方程[18–20],抛物方程[21].因此,怎样利用H1-Galerkin方法得到非线性发展方程无网格比的超收敛结果是值得深思的.
最后,对于线性化的全离散格式来说,由于当时时刻的时间层分析需要用到上一时刻时间层的结论,我们往往会选择数学归纳法进行证明.但是对于每一个时间层的结果到最后都应该由一个统一的系数来控制这个问题显然就不是一件容易的事了.更进一步地,根据不同非线性问题的具体特点,针对不同方程的逼近格式,设计新的高效的有限元数值算法来验证理论分析的正确性也是必须且困难的.
最近,我们在文献[22–34]中,在分裂思想的基础上,博采众家之长,创新性的把无网格比、高精度分析与非协调单元、新的线性化离散格式等特色和优势有机结合起来,形成非线性发展方程在全离散格式上无网格比约束的有限元超收敛分析的一套新理论体系.与此同时,更是尝试着探索、研究一些特殊的方程,考虑绕过分裂的方法也达到无网格比的超收敛结果.
近期所做的工作,主要的创新点集中表现在以下几个方面:
(1)超收敛结果对方程解的光滑性要求比较高,但构造时间离散辅助问题(即时间离散方程系统)时,在多边形区域(例如矩形)下,就无法保证其解较强模的有界性.因此我们利用了一些特殊的、不同以往的技巧,在其解空间较弱的条件下得到无网格比超收敛的结论;巧用Taylor展开式对非线性项进行处理,以保证对时间步长τ的阶不丢失.
(2)由于选择的全离散格式是线性化的形式,在利用数学归纳法分析第n层的结果时需要用到第n−1层的结论,我们用一个统一的系数来控制每一个时间层的结果,这也是其数学归纳法成立的关键所在.
(3)构造了非线性双曲方程新的二阶格式,以此得到无网格比超收敛结果.而以往对非线性双曲方程的无网格比研究甚至连收敛性也没有见到报道.
(4)对一些特殊的非线性发展方程,抛弃分裂误差思想,采用一些新的技巧也证明了其无网格比超收敛性.
本文的目的是在前期我们所做的工作的基础上,挑拣出有特色的创新点给予说明,以期窥探出对非线性发展方程无网格比超收敛分析的重要方法和思路,起到抛砖引玉的作用.
2 非线性抛物方程的无网格比超收敛分析
非线性抛物方程有着深刻的物理背景,它的有限元方法也越来越受人们关注.例如:文献[35]针对一般的非线性抛物方程建立了两种线性化的格式,当τ≤h时,利用线性三角形元得到了L2-模意义下的收敛结果.文献[36]在限制下利用两层时间离散的方法讨论了非线性抛物方程的最优误差估计.文献[37]采用了一个非线性H1投影,当τ4=O(hq),q≤3时,得到了其解在L2-模和H1-模意义下的最优误差估计.文献[1]利用分裂技巧摆脱了此类限制,给出了一类称之为Joule Heating的非线性抛物型方程的协调元无网格比收敛性分析.我们看到,一方面,一般的非线性抛物方程中的非线性项∇·(a(u)∇u)的处理对于超收敛的分析是很有挑战的,特别是在分析空间误差的时候,怎样处理a(u)才可以在不降阶的情况下使其结果能提出空间网格参数h,才能在使用逆不等式的时候不产生网格比,但同时还得能维持数学归纳法所需要要的系数统一性?另一方面,当非线性抛物方程右端的非线性项是局部Lipschitz连续时,对有限元解的正则性要求可能会更苛刻,如何把这些限制考虑进去且得到无网格比超收敛结果是我们想要研究的方向之一.
考虑如下非线性抛物方程
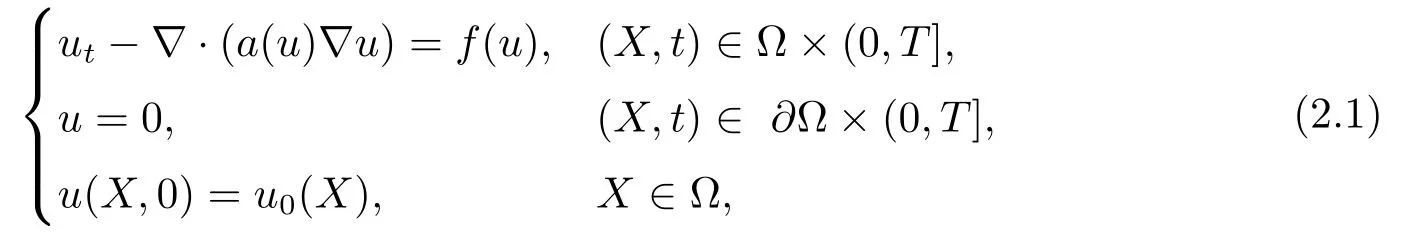
其中Ω⊂R2是一个矩形,其边界为∂Ω,0 首先,设f(u)是Ω上整体Lipschitz连续的函数,Ω是一个四条边都平行于坐标轴的矩形,Γh是一个拟一致正则矩形剖分.对于给定的K∈Γh,令其四个顶点和四条边分别为ai,i=1∼4和.记.定义非协调有限元空间: 其中[vh]表示vh跨过单元边界F的跳度,而当F⊂∂Ω时,[vh]=vh.令Ih:H1(Ω)→Vh为相对应的插值算子,且Ih=Ih|K满足 则文献[21,38–40]证明了下面重要引理. 引理1若,则对于任意的vh∈Vh,有 这里∇h表示分片梯度,且是Vh上的一个能量模.文献[40]证明了对于任意正整数m,vh∈Vh, 设{tn:tn=nτ;0≤n≤N}是[0,T]上的一个等距剖分,时间步长为τ=T/N,设,且u(X,tn)=un,若为一列函数.记 利用这些记号,考虑(2.1)式的线性化Galerkin有限元逼近:寻找,使得对于任意的vh∈Vh0, 第一步 建立一个时间离散系统,当n>1时求Un满足 当n=1时,利用以下式子计算U1: 和 其中U1,0(X)|∂Ω=0,U1(X)|∂Ω=0. 令e1,0,u1−U1,0,en,un−Un(n=0,1,2,···,N). 通过分析时间误差,给出U1,0,Un(n=0,1,2,···,N) 的正则性. 设u和Um(m=0,1,2,···,N) 分别为 (2.1)和(2.9)–(2.11)式的解,u∈L∞(0,T;H3(Ω)),ut,utt∈L∞(0,T;H2(Ω)),uttt∈L∞(0,T;L2(Ω)),则对于m=1,···,N,存在τ0>0,使得当τ≤τ0时,有 和 其中C0是一个与m,h和τ无关的正数. 此时,注意到由于Ω是矩形,其边界不属于C1,那么就不容易得到Un的H3-模有界性.因此随后的无网格比超收敛分析需要利用新的方法得到. 第二步讨论空间误差,也为最终无网格比超逼近结果kIhun−做好准备.给出记号 第三步令 在这个过程中注意到,将τ从内积的一端转向另一端的恒等变化 化简过之后需要估计误差 如果按照传统的方法,则有 这样最终的结果会降一阶.但是若利用Taylor展开则有 其中 这样就可以保持到想要的结果. 限制f(u)为局部Lipschitz连续的,利用双线性协调单元可研究(2.1)式的无网格比超逼近性质(区域及剖分如前面一样).定义其有限元空间Vh0为 其中Ih:H2(Ω)→Vh0是相对应的插值算子,且对于以上双线性元有以下高精度结果[41]. 引理2若,则对于任意的vh∈Vh0,有 引入时间离散方程:当n≥1时求Un满足 接下来,我们分别就时间误差和空间误差中的新技巧予以说明. 时间误差记,则有 注意到在第n−1层中归纳假设(2.21)式成立后,进一步地得到是必需的.主要表现在以下两个方面. 1.在第n层估计中,误差方程左端有,右端部分在的前提下有估计项 和 可以看到,此时当τ充分小时,在第n层误差方程的右端才可以去掉. 2.由于f的局部Lipschitz连续,要想估计误差方程右端项,则必须得有做前提,这样就保证了 空间误差注意到,由于f的局部Lipschitz连续,在估计下面误差时, 利用前面的结论以及协调元的性质,有 这样可以估计得到 注1更进一步地,我们在文献[34]中将文献[10–12]中的混合元和无网格比的思想有机的结合起来,利用分裂内积等思想,得到了(2.1)式关于原始变量u的H1-模和~p=∇u的L2-模的无网格比超收敛结果. 其中Ω同(2.1)式,i是虚数单位,u0(X)是已知复值函数.另外,f(s)是一个实值函数,且关于s是二阶可导连续的. 选用上一部分的区域,剖分和双线性元单元,且仍定义其有限元空间为Vh0.令Rh:是定义在Vh0上的相对应的Ritz投影算子 有 且 更进一步地,当u∈H3(Ω),又由文献[13]可知 其中Ih是定义在Vh0上相对应的插值算子.下面我们仍采用了分裂技巧,分别给出时间误差和空间误差上分析时所遇到的困难和解决方法. 时间误差对于CN格式将误差方程相邻两层相减,则 就变成 至此,得到的结果kenk2=O(τ2)相关估计,可以比文献[8]的结果高二分之一阶,也就是这样的结果导出了,为后面的无网格比超逼近结果奠定了基础. 对于BE格式得到结果kenk2=O(τ)比文献[7]中的结果阶高二分之一阶,这也导出了,也为下面的空间误差做出了铺垫. 空间误差1.对误差方程相邻两层相减,对比文献[45]中的结果,可以看到不需要的有界性也得到了无网格比高精度的结果,这就改进了已有结论. 2.使用插值算子和投影算子相结合的思想:若仅使用插值算子,为了得到高精度结果,避免不了利用高精度结果(∇(un−Ihun),∇vh)=O(h2)kunk3kvhk1或者(∇(un−Ihun),∇vh)=O(h2)kunk4kvhk0,则对Un和un的正则性要求过于苛刻.然而,在Ω为一个矩形的前提下,目前只能得到kUnk2的有界性,此时选用投影算子Rh是合适的.另一方面,若仅仅使用投影算子Rh,则不能构造相应于Rh的插值后处理算子,也就不能得到整体超收敛结果了. Sobolev方程起源于流体通过裂隙岩石的流动、二阶流体的热力学剪切和粘土的固结等物理现象.到目前为止,已有很多文献研究了它的数值方法.例如:文献[46]得到了当τ=O(hd/3)(d≤3)时,在三种情况下关于H1-模最优误差估计结果.而文献[47]利用混合有限元方法,在条件τ=O(h)下得到了最优误差估计.文献[38]控制条件为τ=O(h1+ε)(ε>0)时分别利用协调有限元和非协调有限元讨论了其特征有限元方法,也得到了H1(Ω)-模和L2(Ω)-模的最优误差估计. 大家都知道,H1-Galerkin方法是一个不需要满足LBB条件的混合有限元方法,加上一些技巧的应用,还可得到关于流量~p=∇u散度模的误差估计.但是由于H1-Galerkin混合有限元方法需要的时间离散方程解的正则性较高,在矩形区域下不容易得到,所以对于一般的诸如非线性抛物方程利用上述分裂技巧直接处理暂时还不能去掉h和τ的比值.非线性Sobolev方程有着其自身的特点,它比非线性抛物方程多了一个非线性的导数项,正是多了这一项,使得我们考虑在分析的时候可以不用以上的分裂法就得到无网格比超收敛结果.因此我们通过与前面不同的分析,不引进时间离散方程,即在不必考虑所谓的时间误差的前提下,避免由于时间离散方程解的正则性达不到相应的要求而带来的麻烦,给出了无网格比的超逼近结论. 考虑如下非线性Sobolev方程: 这里对于正数b1,有|b(u)|≤b1,其余同(2.1)式中的假设. 当n=1时, 和 下面先给出一个新的引理. 引理3对于任意的,则有 图1 其中l1,l3分别为K的下边和上边,l2,l4分别为K右边和左边,则有 由引理3,并利用数学归纳法,可分以下几步分析说明非线性Sobolev方程的无网格比超收敛结果 第一步. 第二步利用,得到 利用Gronwall引理,当τ充分小时有 所以 第三步进一步地, 将(4.9)式代入(4.10)式,当τ充分小,利用Gronwalls引理有,再利用(4.9)式得到kξnkh≤Ch2+Cτ2. 这里强调以下三点 (1)如果直接估计kξnkh,对τ和h的比例限制将不可避免; 在物理上,双曲方程是一类一直很受关注的偏微分方程,它可以用来描述声波和电磁波的传播等现象,其中也有很多文献关注其非线性问题的有限元方法.例如,文献[48]和[49]分析了非线性双曲方程的全离散格式,其中文献[48]讨论了混合有限元方法,达到了最优误差估计.文献[49]利用Galerkin交替方向法讨论了一类三维非线性双曲方程,利用先验估计的结果得到了误差的H1(Ω)-模和L2(Ω)-模.但上述结果也都没有摆脱h和τ的比值限制,在文献[48]和[49]中分别需要假设条件τ=O(h),hr=O(τ)(1≤r≤k+1,k≥0)和τ=O(h2).因此,如何有效的对非线性双曲方程展开无网格比的研究具有相当重要的科学价值.另一方面,在现有的参考文献中对非线性双曲方程的二阶线性化格式讨论的非常少,怎样构造新的非线性双曲方程的线性化全离散格式,使得其有更好的稳定性以及超收敛结果也值得进行深入的探讨. 考虑如下非线性双曲方程 关于方程的一些基本假设如同第二节. 我们将对(5.1)式创造性地构造一个新的线性化二阶格式,技巧性地证明其截断误差的二阶性质,给出其相对应的时间离散方程解的正则性,并由此得到在非协调单元下无网格比的超逼近结果. 则有 和 时间误差引入时间离散方程,利用其解Un分裂误差,通过估计时间误差得到Un的正则性.令,则有 和 注意到,在这一节里针对非线性双曲方程构造了一个新的线性化的二阶格式,可以看到要证明其截断误差为O(τ2)是非常不容易的.另一方面,在得到误差结果时,由于C0在第n层和第n+1层必须统一,则在估计误差时,我们需要利用ēm+1≤τ(m≤n−1),而不是ēm+1≤C0τ2(m≤n−1)来得到结果. 空间误差利用以上结果得到超逼近结果,令,则有 在此过程中,有以下几点需要特别关注 2.(5.8)式的右端不能直接被估计成C1(h2+τ2),否则h和τ的比值将无法避免.事实上,也不能将其估计为C1h,因为利用数学归纳法,我们需要统一n层和n+1层的,所以利用了. 进一步地,在误差估计过程中会出现以下项 如果利用类似前面的估计方法,将τ从内积的一端转向另一端,则有结果,这时将不可避免的出现网格比. 为了克服关键问题,重新分裂内积为 则有 最后可导出以下结果 首先,把原来文献中已有的对非线性发展方程无网格比收敛的结果,进一步延伸到对非线性发展方程无网格比的超逼近和超收敛的研究中.由于要想得到高精度的结果,对原始方程解正则性的要求往往都会比较高.那么怎样绕过在矩形区域下,引入的时间离散方程解的有界性达不到H3(Ω)时,有技巧的得到无网格比超逼近结果是之前文献所不曾见过的. 其次,对于非线性发展方程,其非线性项中a(u)的处理也是之前很少有的.我们创新性的利用Taylor展开式,保持了最后时间方向上的误差不丢失阶. 再次,在分析过程中发现,对于一些方程,若仅仅利用插值算子将会提高对方程解的正则性要求;仅仅利用投影算子,没有办法进行插值后处理,进而没有办法得到整体超收敛的性质.所以在对非线性Schrdinger方程的分析当中,利用了插值算子和投影算子相结合的处理方式得到了其无网格比超逼近和超收敛的结果. 而后,由于分裂误差的做法使得引入时间离散方程解在矩形区域下正则性结果不是很好,而此时想要利用H1-Galerkin有限元方法得到无网格比超逼近结果还是非常困难的.对于非线Sobolev方程来说,我们发现了此类方程自身的特点,创新性地抛弃了分裂误差的方法,利用一些特殊的技巧也得到了到了其无网格比超收敛结果. 最后,由于还没有文献对非线性双曲方程的无网格比讨论过,特别是对其二阶线性化的全离散格式研究还很少有文献进行报道.我们尝试着构造一个新的线性化二阶格式,证明了其截断误差的二阶性质,并给出了无网格比超逼近性质. 对未来的进一步工作,我们提出以下几点供参考 (1)各向异性有限元的研究是目前该领域独具特色和挑战性的又一前沿热点和难点(参见文献[50–53]).怎样把原来已有的拟一致的正则剖分下的无网格比超收敛结果拓展到各向异性剖分上去.另一方面,如何将目前只对矩形区域进行的无网格比超收敛研究拓展到一般区域. (2)二重网格算法是处理非线性问题的有效方法(参见文献[54,55]),但在误差估计中粗网格的网格参数或者细网格的网格参数都会不可避免的和时间步长产生一个比值.事实上,我们在文献[22]中已经讨论了半线性抛物方程二重网格算法的无网格比收敛性.那么怎样才可以得到非线性发展方程二重网格算法的无网格比高精度分析呢?由于二重网格算法在粗网格上往往是给出一个非线性的逼近方程,要去掉网格比约束条件,便要每一层都引入一个非线性的时间离散方程.这样,非线性系数的有界性在当时时间层是未知的,得到它的有界性便是非常困难的事了.另一方面,二重网格算法需要利用粗网格的结果得到在细网格上的逼近方程,使得它每一层都是一个线性问题,那么此时使用光滑边界来提高此处引入的另一组时间离散方程系统解的正则性也许是可行的办法,但这样再处理超收敛分析就是一个挑战了. (3)很多数学物理问题都需要利用积分微分方程进行求解.数学、工程技术和自然科学的许多领域,例如在系统识别、流体力学、信号重构与图像恢复、电磁场理论与静电学、地球物理勘探等方面都将归结为求解积分微分方程的问题.积分微分方程已经成为众多学者研究的一份重要方向.更值得一提的是,对于我们比较难以处理的双曲方程,也可以利用ut=q使其变成一个抛物型的积分微分方程.对于积分微分方程的无网格比收敛性研究,现在还没有涉及到,尤其是该如何解决其积分项的估计都还是待解决的问题,因此这方面的工作还有待进一步地研究. (4)怎样将无网格比超收敛高精度结果进一步推广应用到更为复杂的二阶问题上去,比如说非定常不可压缩Navier-Stokes方程?事实上,人们对于该方程的有限元方法做了大量研究,如协调有限元方法、全离散加罚有限元方法、多尺度方法、稳定化有限元方法等[56–58].关于无网格比,文献[59]利用特征有限元方法绕过了Navier-Stokes方程的非线性项的繁琐,再利用分裂技巧得到了无网格比收敛的结果.那么如果换成一般的有限元方法,处理它的非线性项使得无网格比结果不掉阶是一个麻烦的事情.关于非线性四阶问题[59–61](如EFK方程、Cahn-Hilliard方程、四阶非线性双曲方程等)的无网格比超收敛研究也是我们所关心的话题.事实上,对于非线性的Navier-Stokes或者是四阶问题,混合有限元方法是常用的一个方法,那么怎样利用它得到这些问题的无网格比超收敛结果也是我们未来研究的方向之一. 以上这些问题都是全新的、悬而未决的关键性问题,作为延伸和后续的工作,亟待建立一套新的框架性理论体系和分析模式去深入展开对这些问题的研究和探索.可以说,任何实质性的创新和突破都将进一步丰富有限元方法的内涵,提升其品味.2.1 非协调有限元方法
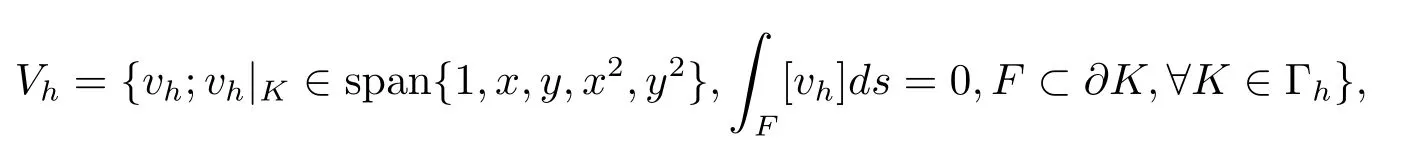
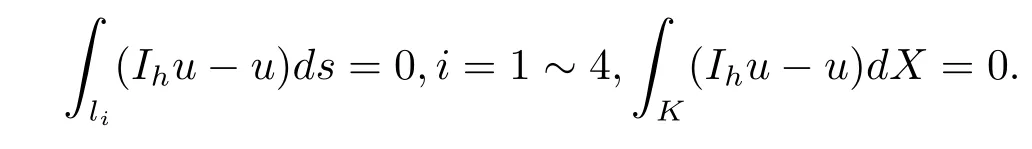
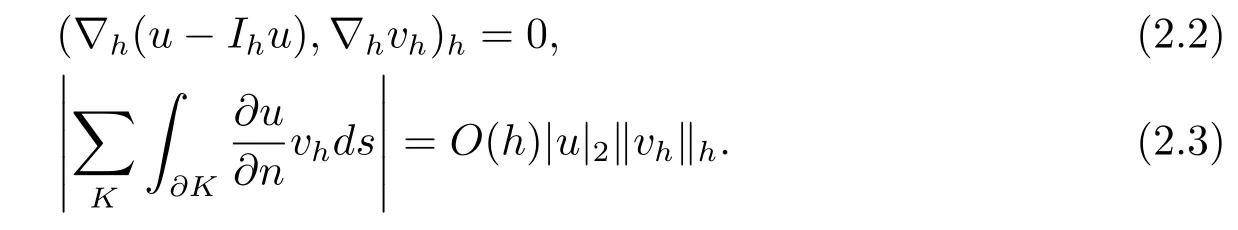
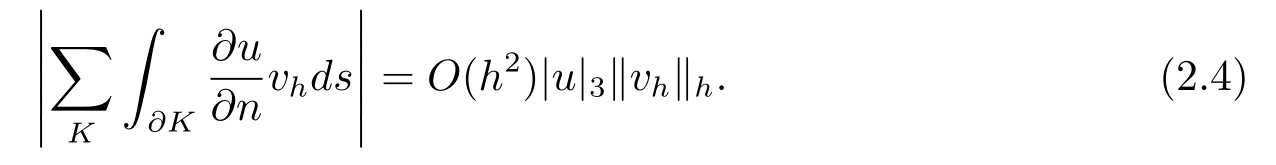

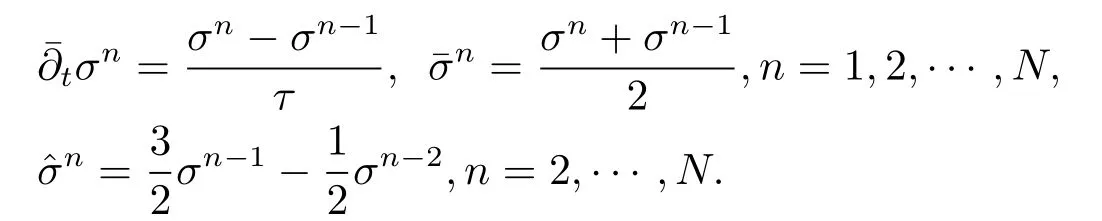

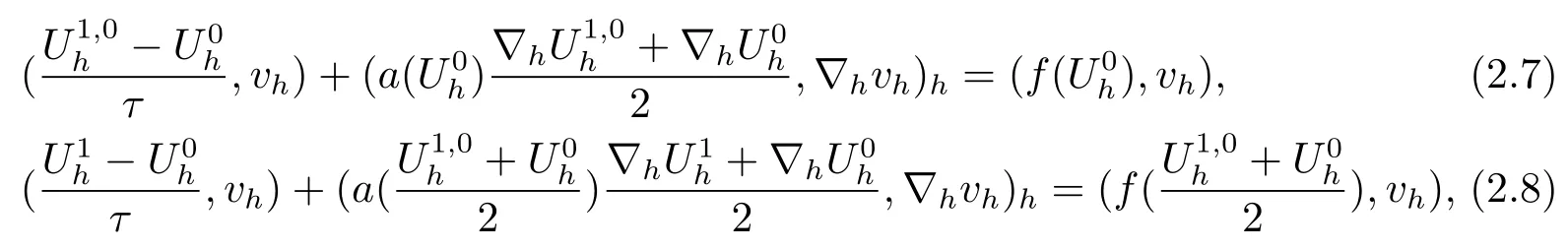
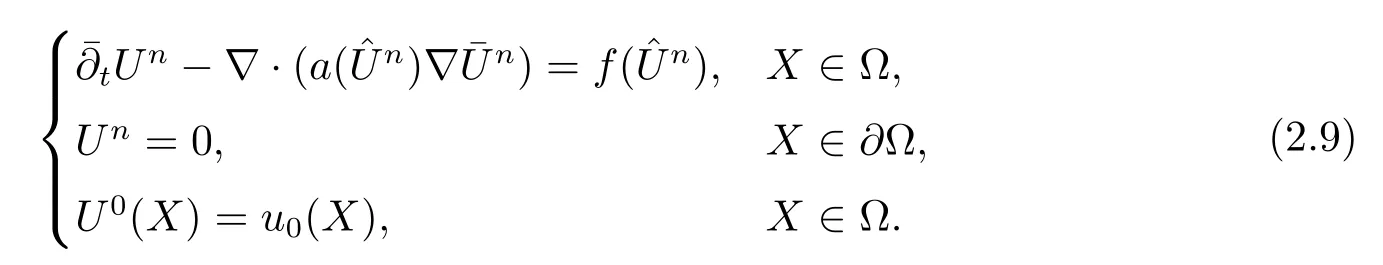
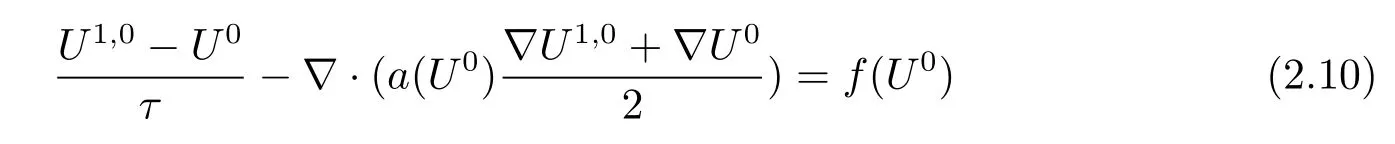
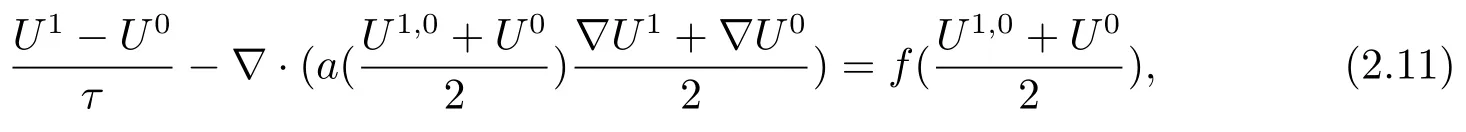

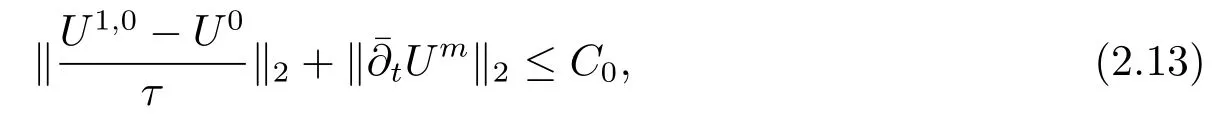
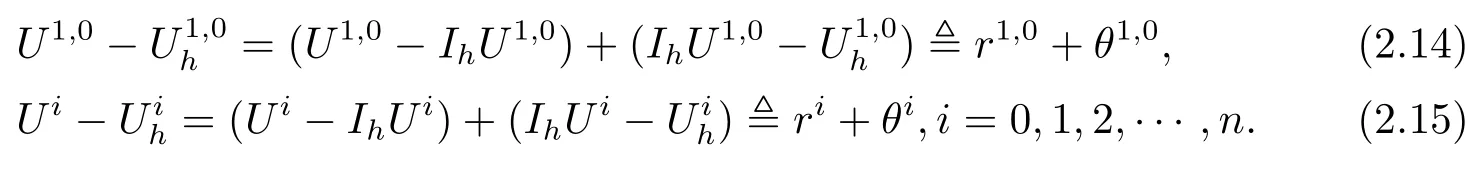
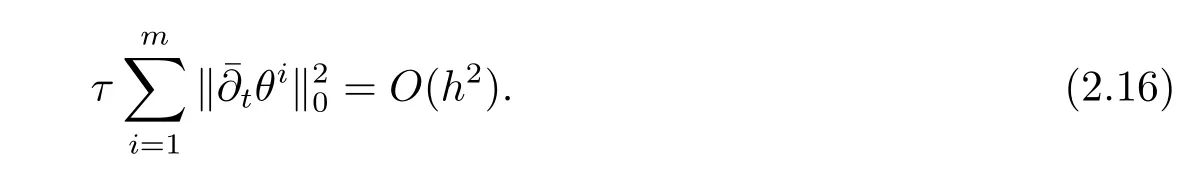
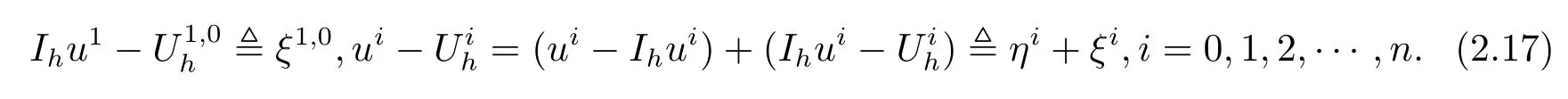

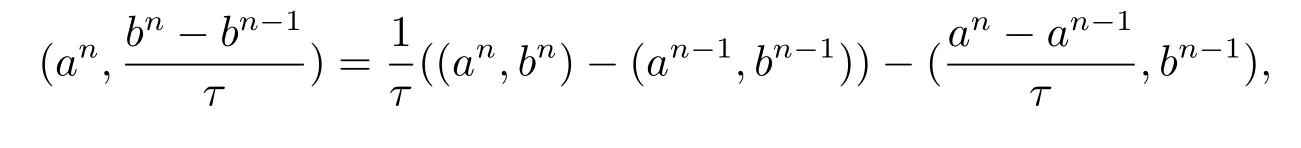
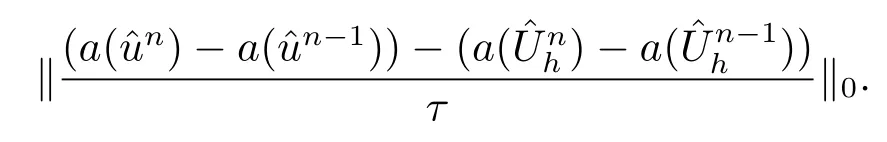

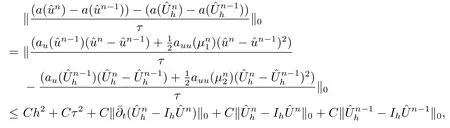
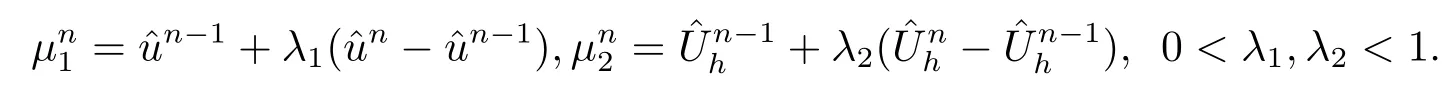
2.2 协调有限元方法
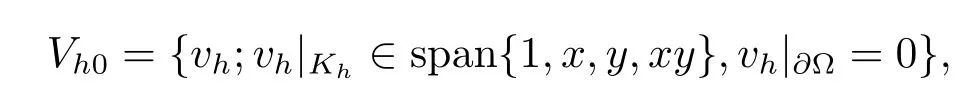
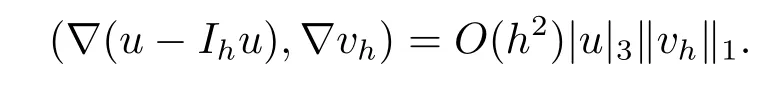

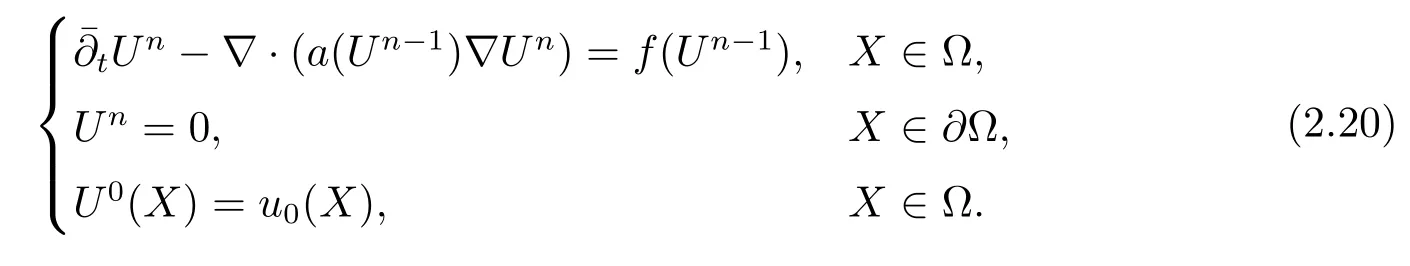
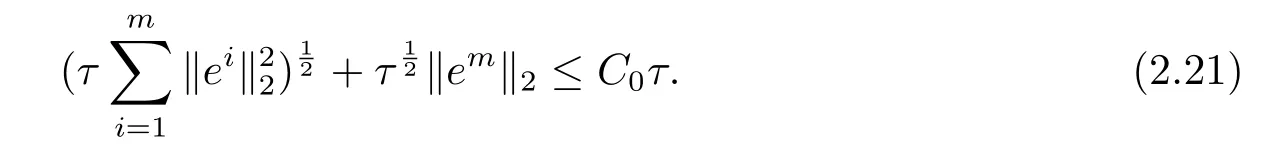
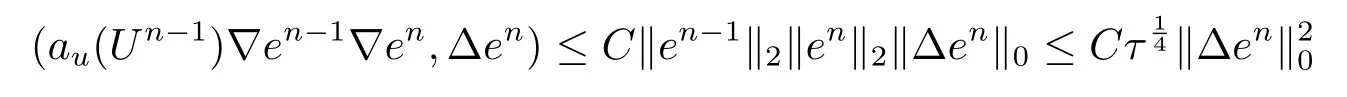
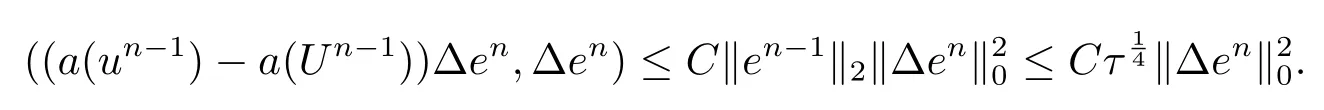
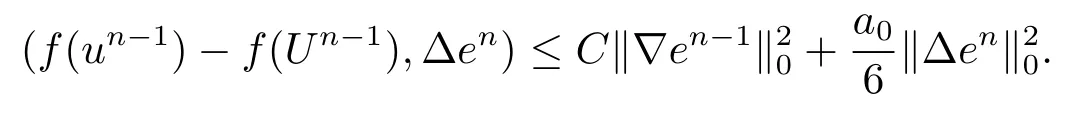
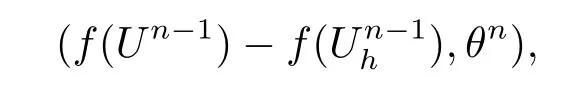
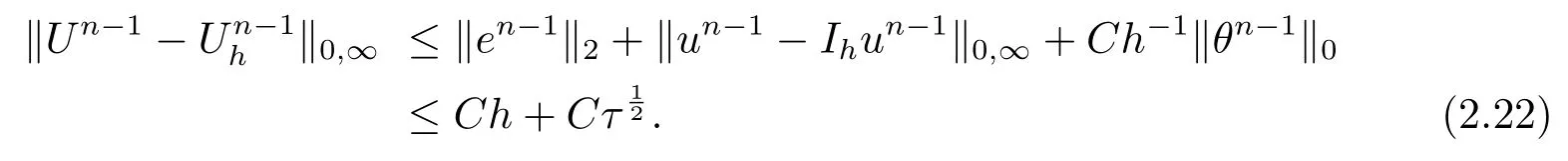
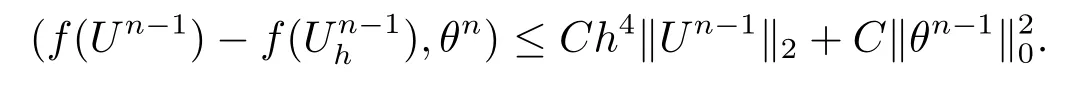
3 非线性Schrdinger方程的无网格比超收敛分析
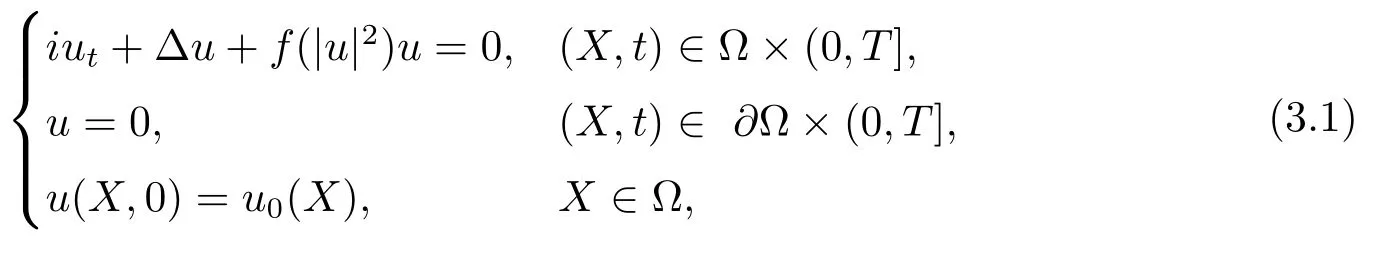


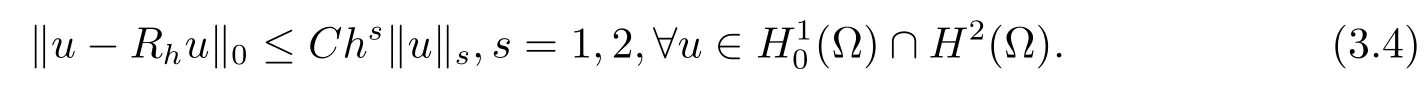
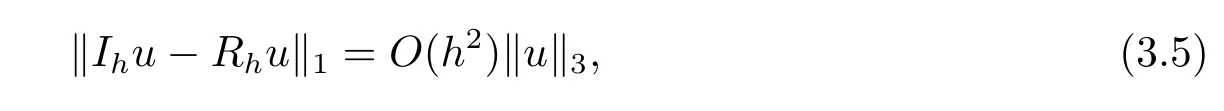
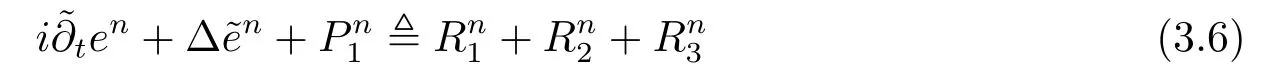

4 非线性Sobolev方程H1-Galerkin混合有限元方法的无网格比超收敛分析
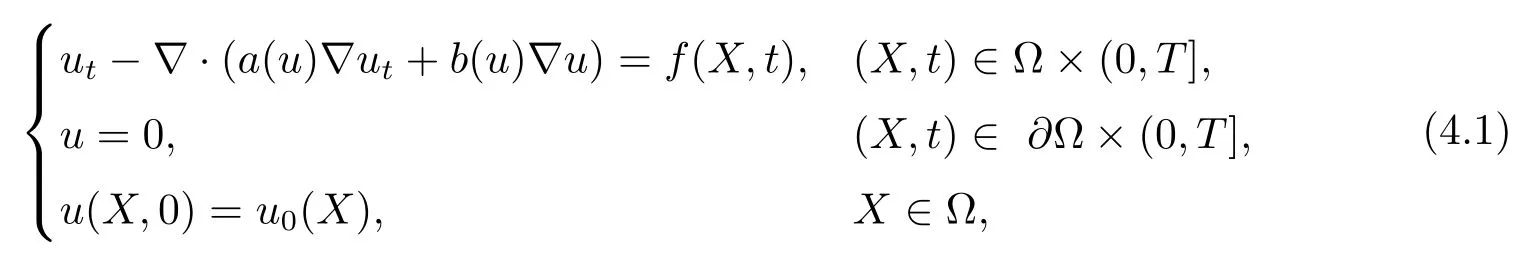
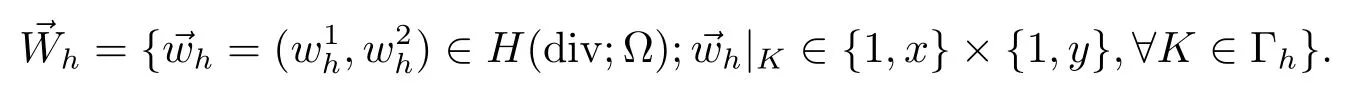

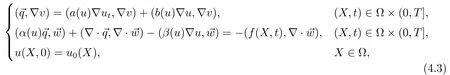
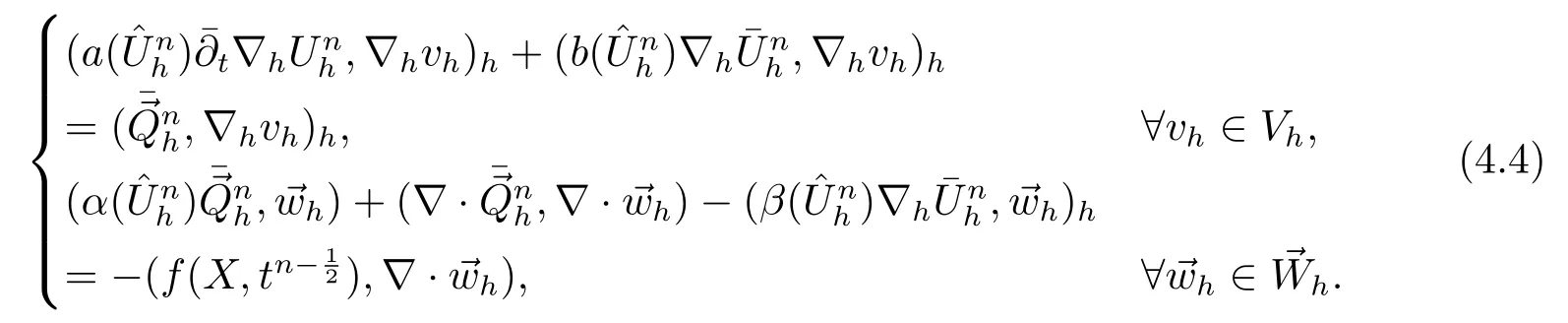

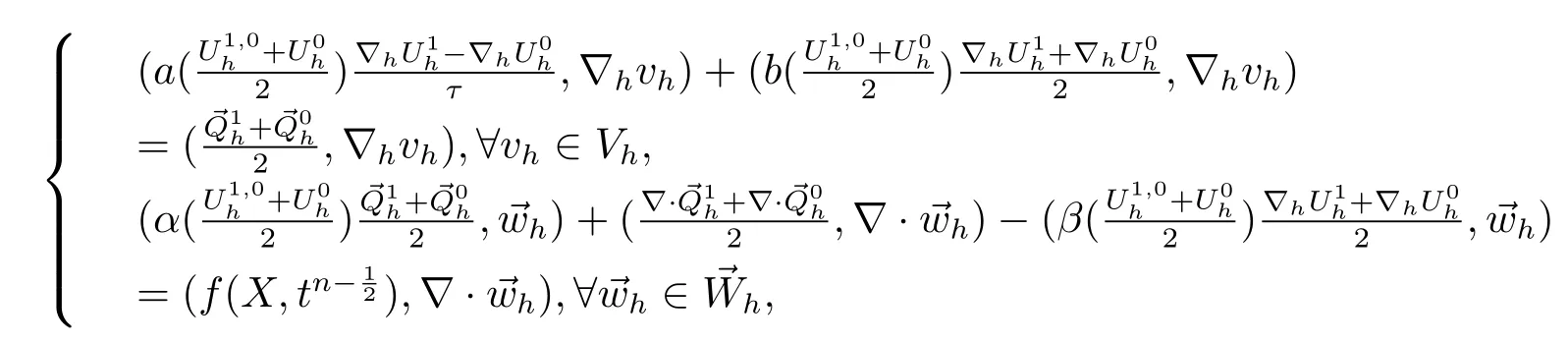
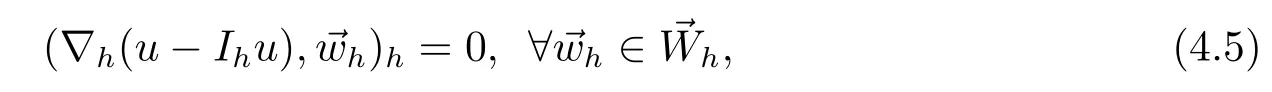
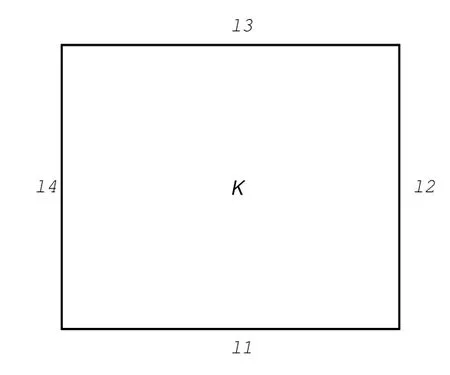

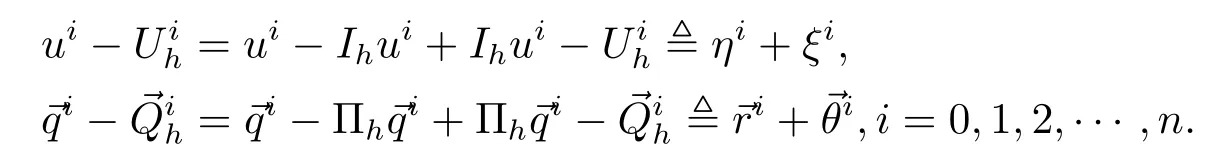

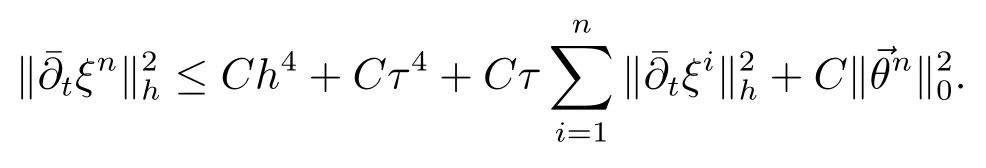
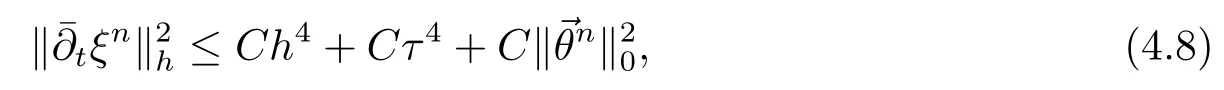
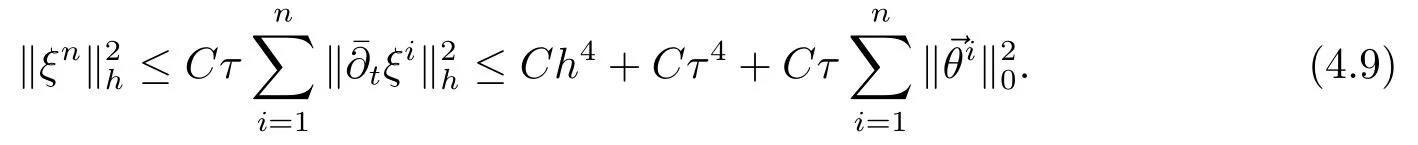
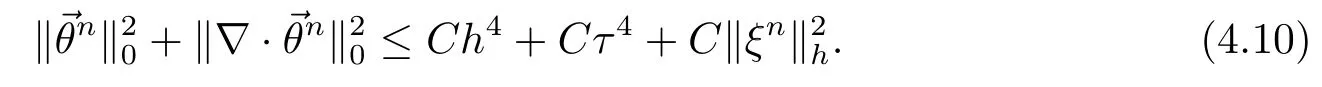
5 非线性双曲方程
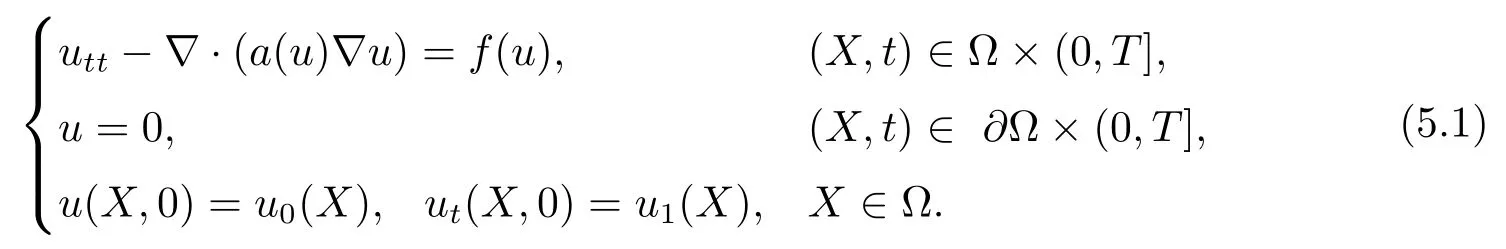
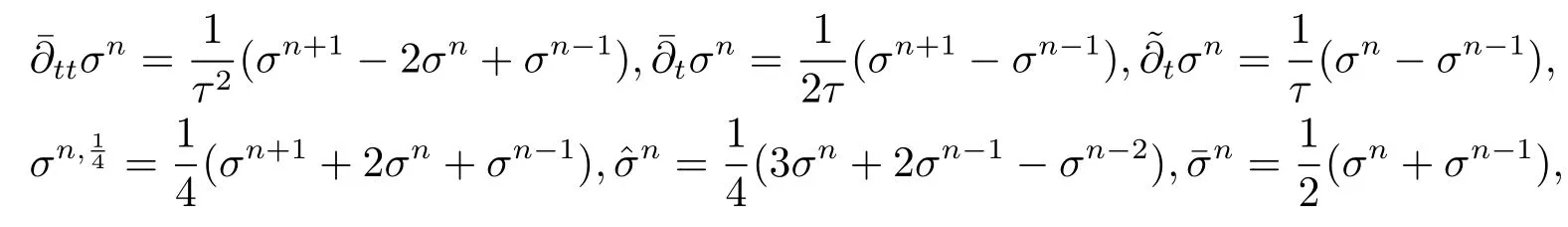
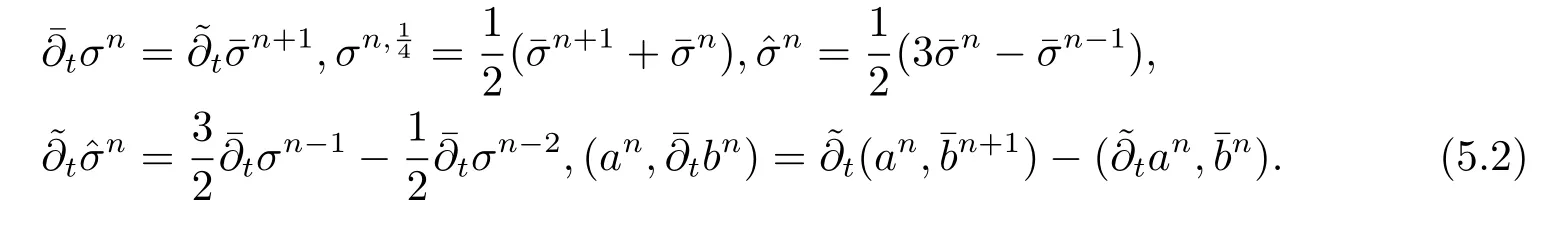
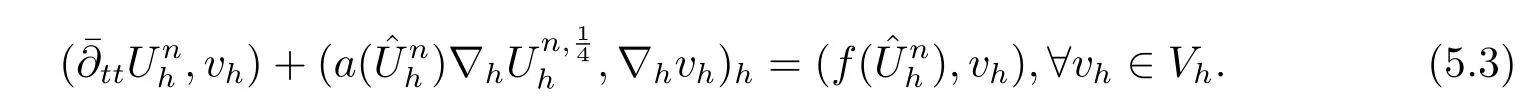
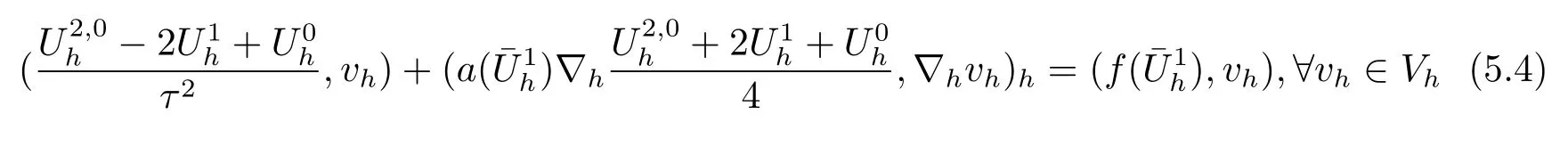
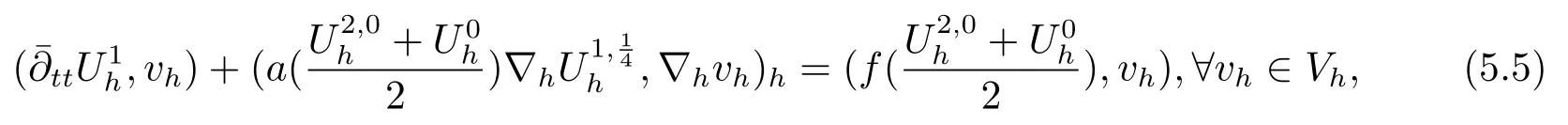
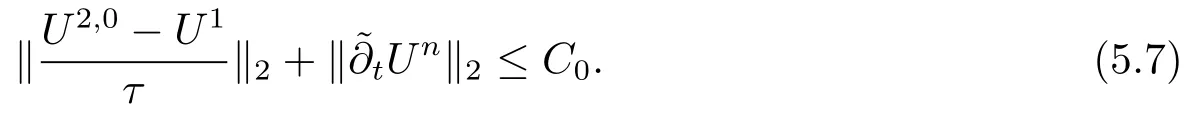

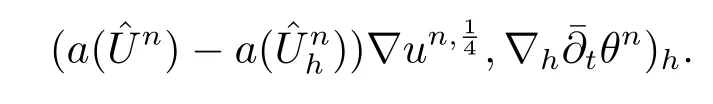
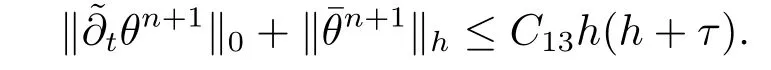

6 总结与展望

